Алгоритмы обучения

Искусственные нейронные сети обучаются самыми разноо 19419s1823t 73;разными методами. К счастью, большинство методов обучения исходят из общих предпосылок и имеет много идентичных характеристик. Целью данного приложения является обзор некоторых фундаментальных алгоритмов, как с точки зрения их текущей применимости, так и с точки зрения их исторической важности. После ознакомления с этими фундаментальными алгоритмами другие, основанные на них, алгоритмы будут достаточно легки для понимания и новые разработки также могут быть лучше поняты и развиты.

w_ij(t+1) = w_ij(t) + NET_i NET_j,

w_ij(t) - сила синапса от нейрона i j t; NET_i NET_j -

NET

NET_j NET j OUT_i - i;w_ij i j

w_ij(t+1) = w_ij(t) + OUT_i OUT_j

w_ij(t) - сила синапса от нейрона i к нейрону j t; OUT_i F(NET_i); OUT_j - F(NET).

w_ij(t+1) = w_ij(t) + [OUT_i(t) - OUT_i(t-1)][ OUT_j(t) - OUT_j(t-1)],

w_ij(t) - сила синапса от нейрона i к нейрону j t; OUT_i(t) - выходной уровень пресинаптического нейрона в момент времени t; OUT_j(t) t

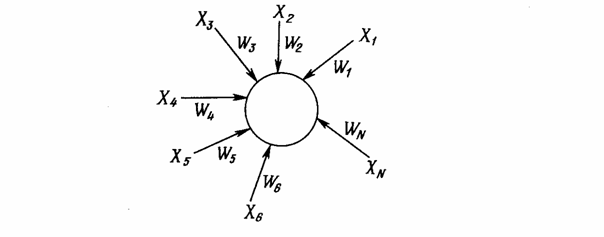
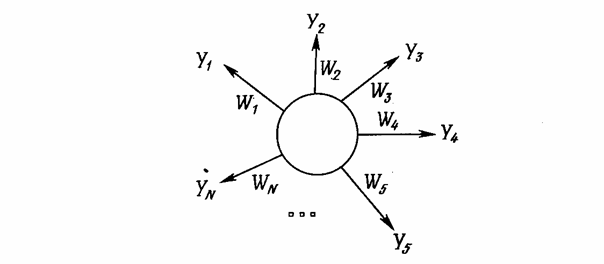
Много общих идей, используемых в искусственных нейронных сетях, прослеживаются в работах Гроссберга; в качестве примера можно указать конфигурации входных и выходных звезд [I], используемые во многих сетевых парадигмах. Входная звезда, как показано на рис. Б.1, состоит из нейрона, на который подается группа входов через синапсические веса. Выходная звезда, показанная на рис. Б.2, является нейроном, управляющим группой весов. Входные и выходные звезды могут быть взаимно соединены в сети любой сложности; Гроссберг рассматривает их как модель определенных биологических функций. Вид звезды определяет ее название, однако звезды обычно изображаются в сети иначе.

w_i(t+1) = w_i(t) + a[x_i - w_i(t)],

w_{i i i} - i-й вход; a

a

w_i(t+1) = w_i(t) + b[y_i - w_i(t)],

b

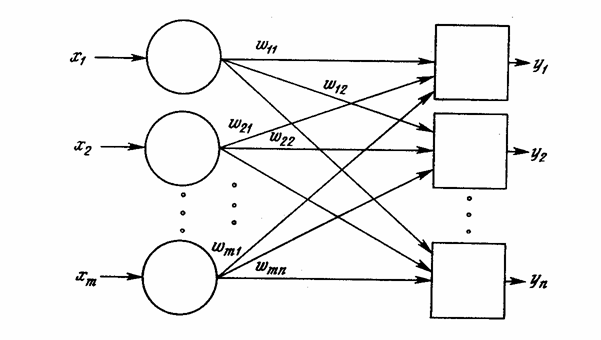
NET

.

NET

OUT_j = 1, NET_{j j}

OUT_j =

_j j

error_j = target_j - OUT_j.

Каждый вес модифицируется следующим образом:

W_ij(t+1) = w_ij(t) +ax_ierror_j.

NET OUT.

error_j = target_j - NET_j.

n n-

D_j n- W_j

_i i входного вектора X, w_ij i j

Нейрон, который имеет весовой вектор, самый близкий к X, объявляется победителем. Этот весовой вектор, называемый W_c, становится основным в группе весовых векторов, которые лежат в пределах расстояния D от W_c

W_j(t+l) = W_j(t) + a[X - W_j(t)]

для всех весовых векторов в пределах расстояния D от W_c

В процессе обучения нейронной сети значения D и a a , в то время как D может в начале обучения равняться максимальному расстоянию между весовыми векторами и в конце обучения стать настолько маленьким, что будет обучаться только один нейрон.

Grossberg S. 1974. Classical and instrumental learning by neural networks. Progress in theoretical biology, vol. 3, pp. 51-141. New York: Academic Press.

Hebb D. O. 1949. Organization of behavior. New York: Science Editions.

Kohonen T. 1984. Self-organization and associative memory. Series in Information Sciences, vol. 8. Berlin: Springer verlag.

Rosenblatt R. 1959. Principles of neurodynamics. New York: Spartan Books.

Widrow B. 1959 Adaptive sampled-data systems, a statistical theory of adaptation. 1959. IRE WESCON Convention Record, part 4. New York: Institute of Radio Engineers.

Widrow В., Hoff M. 1960. Adaptive switching circuits. I960. IRE WESCON Convention Record. New York: Institute of Radio Engineers.