Післяоптимізаційний аналіз задачі лінійного програмування, особливо для прикладних досліджень, є не менш важливою частиною лінійного програмування, ніж знаходження оптимального розв’язку задачі. Як зазначалося вище, задачі лінійного програмування є найпростішим типом задач математичного програмування. Лінійні економіко-математичні моделі простіші через те, що в них не беруться до уваги впливи випадкових чинників на економічні процеси (об’єкти), що моделюються; динамі 838h73i чні процеси замі 838h73i нюють їх можливими статичними аналогами; використовують лінійні функції замі 838h73i сть нелінійних, які точніше описують залежності між економічними показниками, тощо. Очевидно, що за таких допущень більшість параметрів задач лінійного програмування є наближеними величинами. Тому важливим є питання визначення діапазону стійкості оптимальних планів прямої та двоїстої задач. У даному розділі буде розглянуто вплив змін параметрів задачі, в межах яких структура оптимального плану залишається постійною, а також методи визначення ступеня змін значень оптимального плану, якщо його структура порушується.
![]() (3.36)
(3.36)
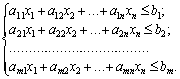 (3.37)
(3.37)
![]() (3.38)
(3.38)
для якої знайдено оптимальний план. Остання симплексна таблиця має вигляд (табл. 3.2). Не обмежуючи загальності, можна вважати, що базис утворюють перші m векторів.
Розглянемо
вплив на
оптимальний
план задачі
зміни таких параметрів,
як
компоненти
вектора обмежень
![]() ; коефіцієнти
цільової
функції
; коефіцієнти
цільової
функції ![]() ;
коефіцієнти
матриці
системи обмежень
(3.37) —
;
коефіцієнти
матриці
системи обмежень
(3.37) — ![]() .
.
|
сm |
cm |
cn |
||||||||
|
x |
x |
xm |
xm |
xn |
||||||
|
x |
|
|
|
|||||||
|
x |
|
|
|
|||||||
|
m |
xm |
сm |
|
|
|
|||||
|
m |
|
F |
|
|
||||||
Допустимо,
що деяке k-те
обмеження (![]() ) має в
правій частині
початкове
значення —
) має в
правій частині
початкове
значення — ![]() . Нехай
початкова
величина
змінилась на
величину
. Нехай
початкова
величина
змінилась на
величину ![]() . Отже, k-те
обмеження в
системі (3.37)
буде мати
вигляд:
. Отже, k-те
обмеження в
системі (3.37)
буде мати
вигляд:
![]() . (3.39)
. (3.39)
Для зведення (3.39) до канонічного виду необхідно ввести додаткову змінну xn+k (якщо обмеження має вигляд рівняння, то як таку змінну можна розглядати невід’ємну штучну змінну).
![]() (3.40)
(3.40)
де D
— матриця, що
складена з
компонент
векторів ![]() останнього
базису;
останнього
базису; ![]() —
оптимальний
план задачі
(3.36)—(3.38); В —
вектор, що
складається
з вільних членів
системи
обмежень в
останній
симплексній
таблиці.
—
оптимальний
план задачі
(3.36)—(3.38); В —
вектор, що
складається
з вільних членів
системи
обмежень в
останній
симплексній
таблиці.
Отже,
якщо
змінюються
компоненти
вектора В, то
змінюються
також
значення ![]() . Однак
існує
діапазон, у межах
якого всі
компоненти
. Однак
існує
діапазон, у межах
якого всі
компоненти ![]() залишаються
невід’ємними,
тобто
структура
оптимального
плану не змінюється.
Визначимо ці
межі.
залишаються
невід’ємними,
тобто
структура
оптимального
плану не змінюється.
Визначимо ці
межі.
Вектор ![]() подамо
у вигляді:
подамо
у вигляді:
![]() , (3.41)
, (3.41)
де ek — одиничний вектор-стовпчик, а в ньому одиниця — k-та компонента. Тоді, використовуючи (3.40), маємо:
![]() , (3.42)
, (3.42)
де dk — (добуток матриці D–1 на одиничний вектор ek) k-ий стовпчик матриці D–1.
Позначимо
елементи k-го
стовпчика
матриці ![]() через
через ![]() , тоді:
, тоді:
![]() або
або ![]()
|
сm |
cm |
cn + k |
cn + m |
|||||||||
|
x |
x |
xm |
xm |
xn + k |
xn + m |
|||||||
|
x |
|
a1, m + 1 |
a1, n + k |
a1, n + m |
||||||||
|
x |
|
a2, m + 1 |
a2, n + k |
a2, n + m |
||||||||
|
m |
xm |
сm |
|
am, m + 1 |
аm, n + k |
amn + m |
||||||
|
m |
|
F¢ |
Δm + 1 |
Δn + k |
Δn + m |
|||||||
Оскільки
необхідно,
щоб план ![]() також
був
оптимальним,
ма тора,
отже,
також
був
оптимальним,
ма тора,
отже,
![]() (3.43)
(3.43)
![]() . (3.44)
. (3.44)
Тоді нижньою та верхньою границями зміни значення bk відповідно будуть:
![]() ;
;
![]()
Якщо
не існує
жодного ![]() для
для ![]() , то
, то ![]() , а якщо не
існує ні
одного
, а якщо не
існує ні
одного ![]() для
для ![]() , то
, то ![]() .
.
Для
задачі
знаходження
мінімального
значення цільової
функції та
обмежень
системи типу
«≥» значення Δbk
змінює знак,
оскільки
замі 838h73i сть
нерівності ![]() можна
розглянути
рівносильну
нерівність
можна
розглянути
рівносильну
нерівність ![]() .
.
Отже,
для ![]() за будь-якого
значення
за будь-якого
значення ![]() , що відповідає
додатковій
небазисній
змінній
, що відповідає
додатковій
небазисній
змінній ![]() ,
структура
оптимального
плану задачі
(3.36)—(3.38)
залишиться
постійною.
,
структура
оптимального
плану задачі
(3.36)—(3.38)
залишиться
постійною.
Якщо додаткова змінна xn+k базисна, то це означає, що у виразі (3.42) dk –одиничний вектор з k-ою компонентою, рівною одиниці, отже, система нерівностей (3.43) перетвориться в таку:
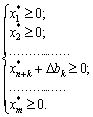
Очевидно, що значення додаткової базисної змінної визначає діапазон змін, в якому відповідна компонента bk може зменшуватись (збільшуватись для обмежень типу «≥»).
Оптимальний
план
залишається
незмінним у
діапазоні bk + Δbk для тих ![]() , яким
відповідають
додаткові
базисні змінні
, яким
відповідають
додаткові
базисні змінні
xn
+ k
![]() (3.45)
(3.45)
 де,
де, ![]() . (3.46)
. (3.46)
. Якщо
компоненти
вектора
вільних
членів системи
обмежень
задачі
лінійного
програмування
змінюються
водночас для
кількох чи
всіх значень ![]() , то
визначення
границь
можливих
змін величин
, то
визначення
границь
можливих
змін величин ![]() стає
надто
складною
проблемою.
Однак у
такому разі
завжди можна
перевірити,
чи задовольняють
конкретні
зміни
величин
стає
надто
складною
проблемою.
Однак у
такому разі
завжди можна
перевірити,
чи задовольняють
конкретні
зміни
величин ![]() систему
виду:
систему
виду:
![]() ,
,
де Е
— одинична
матриця. Якщо
позначити
елементи
матриці ![]() через
через ![]() , тоді:
, тоді:
![]() або
або ![]() .
.
Оскільки
необхідно,
щоб план ![]() також
був
оптимальним,
має виконуватися
умова
невід’ємності
всіх
компонент вектора,
отже:
також
був
оптимальним,
має виконуватися
умова
невід’ємності
всіх
компонент вектора,
отже:
![]() ,
,
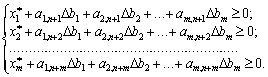 (3.47)
(3.47)
Якщо
значення ![]() задовольняють
всі
нерівності
системи (3.47), то
структура
оптимального
плану задачі
(3.36)—(3.38)
залишається
постійною.
задовольняють
всі
нерівності
системи (3.47), то
структура
оптимального
плану задачі
(3.36)—(3.38)
залишається
постійною.
Для
визначення
верхньої та
нижньої
границь змін ![]() , в межах
яких
структура
оптимального
плану залишається
постійною,
необхідно
розв’язати систему
нерівностей
(3.47). Однак у
більшості випадків
для
знаходження
оптимального
плану нової
задачі
лінійного
програмування
, в межах
яких
структура
оптимального
плану залишається
постійною,
необхідно
розв’язати систему
нерівностей
(3.47). Однак у
більшості випадків
для
знаходження
оптимального
плану нової
задачі
лінійного
програмування
![]() простіше
розв’язати
задачу
симплексним
методом,
змінюючи
вільні члени
системи (3.37) на
простіше
розв’язати
задачу
симплексним
методом,
змінюючи
вільні члени
системи (3.37) на ![]() .
.
D. Для двох
значень ![]() , що
задовольняють
систему (3.47),
причому за
оптимальним
планом
обмеження, що
відповідають
, що
задовольняють
систему (3.47),
причому за
оптимальним
планом
обмеження, що
відповідають
![]() , у системі
(3.37)
виконуються
як рівняння,
можна визначити
норму
замі 838h73i щення, що
показує,
наскільки
необхідно збільшити
(зменшити)
величину
, у системі
(3.37)
виконуються
як рівняння,
можна визначити
норму
замі 838h73i щення, що
показує,
наскільки
необхідно збільшити
(зменшити)
величину ![]() за
зменшення
(збільшення)
за
зменшення
(збільшення) ![]() , щоб значення
цільової
функції
залишилось
незмінним.
, щоб значення
цільової
функції
залишилось
незмінним.
З
третьої теореми
двоїстості
відомо, що за
малих
значень ![]() , тобто за
таких
значень
приросту, які
не змінюють
значення
двоїстих
оцінок, а
отже, задовольняють
систему (3.47),
виконується
рівняння:
, тобто за
таких
значень
приросту, які
не змінюють
значення
двоїстих
оцінок, а
отже, задовольняють
систему (3.47),
виконується
рівняння: ![]() , або
, або
![]() .
.
Нехай
величина br
змінилась на
Δbr.
Визначимо, як
необхідно
змінити bs, щоб
значення
цільової
функції
залишилось
тим самим.
Зміна br
означає, що ![]() ,
аналогічно
за зміни
,
аналогічно
за зміни
![]() на
на ![]() маємо:
маємо: ![]() . Аби
значення функціонала
залишалось
незмінним,
необхідно,
щоб
. Аби
значення функціонала
залишалось
незмінним,
необхідно,
щоб
![]() .
.
Звідси
виразимо
шуканий
вплив ![]() на
на ![]() :
:
![]() . (3.48)
. (3.48)
При відповідній замі 838h73i ні величин br та bs значення цільової фун
Рівняння (3.48) визначає, якою кількістю одного ресурсу можна замі 838h73i нити інший ресурс, щоб цільова функція не змінилась, причому розглядаються лише ті ресурси, які використані повністю при виробництві продукції за оптимальним планом.
Розглянемо
задачу
лінійного
програмування
(3.36)—(3.38). Допустимо,
що
коефіцієнт
цільової
функції при
деякій k-ій
змінній ![]() з
початковим
значенням
з
початковим
значенням ![]() змінився
на величину
змінився
на величину ![]() . Отже,
цільова
функція (3.36)
набуде
вигляду:
. Отже,
цільова
функція (3.36)
набуде
вигляду:
![]() , (3.49)
, (3.49)
де С, Х — відповідно вектор компонент цільової функції та вектор змінних, ek — одиничний вектор-рядок, де одиниця відповідає k-ій компоненті.
. Перший
випадок —
коефіцієнт ck
відповідає
базисній змінній
оптимального
плану. За
припущенням
базисними
змінними
оптимального
плану є перші
m
векторів
останньої
симплексної
таблиці, отже,
![]() .
.
Зміни
коефіцієнтів
цільової
функції в
процесі
реалізації
симплексного
методу
впливатимуть
лише на значення
оцінкового ряду
(![]() ).
).
![]() .
.
![]()
![]() ,
,
де аkj — елементи вектора-рядка, який є результатом множення ek на Х.
|
сk + Δck |
сm |
cm + 1 |
cn |
|||||||||
|
x |
x |
xk |
xm |
xm + 1 |
xn |
|||||||
|
x |
|
a1, m |
|
a1, n |
||||||||
|
x |
|
a2, m + 1 |
a2n |
|||||||||
|
k |
xk |
ck + Δck |
|
ak, m + 1 |
akn |
|||||||
|
m |
xm |
сm |
|
am, m + 1 |
amn |
|||||||
|
m |
Fj – cj |
F¢ |
Δm + 1 |
Δn |
||||||||
![]() (3.50)
(3.50)
![]() . (3.51)
. (3.51)
Тоді нижньою та верхньою границями змін значення сk відповідно будуть:
![]() ;
;
![]() .
.
Якщо
не існує
жодного ![]() для
для ![]() , то
, то ![]() , а якщо не
існує ні
одного
, а якщо не
існує ні
одного ![]() для
для ![]() , то
, то ![]() .
.
Отже,
за змін сk,
що
відповідає
базисній
змінній, в
інтервалі ![]() , якщо
, якщо ![]() , структура
оптимального
плану задачі
(3.36)—(3.38) залишиться
тією самою.
, структура
оптимального
плану задачі
(3.36)—(3.38) залишиться
тією самою.
Зміна
коефіцієнта
цільової
функції небазисної
змінної
впливає на
оцінку лише
цієї змінної.
Допустимо, що
це
коефіцієнт ![]() і за
припущенням
у даній
задачі
і за
припущенням
у даній
задачі ![]() . Нехай цей
коефіцієнт
зміниться на
величину
. Нехай цей
коефіцієнт
зміниться на
величину ![]() . Тоді для
задачі з
цільовою
функцією (3.49) в
останній
симплексній
таблиці
зміниться
лише одна оцінка,
що
відповідає
небазисній
змінній
. Тоді для
задачі з
цільовою
функцією (3.49) в
останній
симплексній
таблиці
зміниться
лише одна оцінка,
що
відповідає
небазисній
змінній ![]() :
:
![]() ,
,
де ![]() —
оцінка
вектора при
змінній
—
оцінка
вектора при
змінній ![]() задачі
(3.36)—(3.38). Дана
оцінка має
бути
невід’ємною,
отже:
задачі
(3.36)—(3.38). Дана
оцінка має
бути
невід’ємною,
отже:
![]() .
.
![]() . (3.52)
. (3.52)
Тобто
для
коефіцієнтів
цільової
функції при
небазисних
змінних
існує лише
верхня межа
зміни
діапазону ![]() .
.
. Якщо
коефіцієнти
при змінних цільової
функції (3.36) задачі
лінійного
програмування
водночас змінюються
для кількох
чи всіх
значень ![]() , то
визначення
границь
можливих
змін величин
, то
визначення
границь
можливих
змін величин ![]() здійснюється
аналогічно
випадку (А).
здійснюється
аналогічно
випадку (А).
Для
того, щоб
план задачі з
цільовою
функцією, в
якій одночасно
змінюються
кілька чи всі
значення ![]() , та
системою
обмежень (3.37), (3.38)
також був
оптимальним,
має
виконуватися
умова,
аналогічна (3.50):
, та
системою
обмежень (3.37), (3.38)
також був
оптимальним,
має
виконуватися
умова,
аналогічна (3.50):
![]() (3.53)
(3.53)
З системи
(3.53) знаходять
діапазон
змін ![]() , для якого
структура
оптимального
плану початкової
задачі буде
незмінною.
, для якого
структура
оптимального
плану початкової
задачі буде
незмінною.
сті, прибутку) одиниць кожного виду продукції, в межах яких визначена оптимальним планом структура виробництва продукції залишається незмінною.
Як
правило,
коефіцієнти ![]() матриці
системи
обмежень
задачі (3.36)—(3.38) є
достовірнішими,
ніж компоненти
вектора
цільової
функції чи
вектора обмежень,
оскільки
вони
здебільшого
є технологічними
коефіцієнтами
(нормами
витрат матеріальних
ресурсів на
виробництво
одиниці
кожного виду
продукції) і
не залежать
від впливу
випадкових
чинників у
такій мірі,
як рівень цін
чи обсяги
ресурсів.
матриці
системи
обмежень
задачі (3.36)—(3.38) є
достовірнішими,
ніж компоненти
вектора
цільової
функції чи
вектора обмежень,
оскільки
вони
здебільшого
є технологічними
коефіцієнтами
(нормами
витрат матеріальних
ресурсів на
виробництво
одиниці
кожного виду
продукції) і
не залежать
від впливу
випадкових
чинників у
такій мірі,
як рівень цін
чи обсяги
ресурсів.
Розглянемо випадок змін лише тих коефіцієнтів, що відповідають небазисним змінним, оскільки зміна значень коефіцієнтів матриці обмежень, що відповідають базисним змінним, приводить до зміни базисної матриці D, і здійснити такий аналіз досить складно.
Розглянемо
k-ту
небазисну
змінну (![]() ) і
відповідний
їй стовпчик з
компонентами
) і
відповідний
їй стовпчик з
компонентами
![]() . Якщо
деяка l-та
компонента
. Якщо
деяка l-та
компонента
(![]() ) (чи кілька компонент)
даного
вектора
зміниться на
величину
) (чи кілька компонент)
даного
вектора
зміниться на
величину ![]() , то за
алгоритмом
симплексного
методу це приведе
до зміни
значення
оцінки
відповідного
вектора —
, то за
алгоритмом
симплексного
методу це приведе
до зміни
значення
оцінки
відповідного
вектора — ![]() .
.
![]() , (3.54)
, (3.54)
або якщо ![]() , маємо:
, маємо: ![]() .
.
Позначимо
через 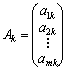 k-й
вектор-стовпчик
матриці сис-
k-й
вектор-стовпчик
матриці сис-
теми обмежень, що відповідає k-ій небазисній змінній. Нехай для деякого k виконується рівність:
![]() . (3.55)
. (3.55)
Розрахуємо
значення
оцінки
вектора![]() ,
підставляючи
в (3.54) нові
значення
,
підставляючи
в (3.54) нові
значення ![]() :
:
![]() . (3.56)
. (3.56)
![]() . (3.57)
. (3.57)
Отже,
розв’язок
залишається
оптимальним
у такому
діапазоні
змін ![]() :
:
![]() , якщо
, якщо ![]() ; (3.58)
; (3.58)
![]() , якщо
, якщо ![]() . (3.59)
. (3.59)
нерівностей
(3.58), (3.59) полягає в
тому, що вони
дають змогу
визначати
межі
можливих
змін норм витрат
ресурсів на
виробництво
одиниці продукції,
в яких
оптимальна
структура
виробництва
продукції
залишається
незмінною. Розглянутий
випадок
стосується
зміни коефіцієнтів
аij ![]() для
тих видів
продукції,
виробництво
яких за
оптимальним
планом є
недоцільним.
З першого
погляду
здається, що
таке дослідження
є
беззмістовним.
Однак
виконані
розрахунки
містять додаткову
інформацію,
яку можна
використати
для
прийняття
управлінських
рішень у виробництві,
приміром
визначити, у
який спосіб
необхідно
змінити
норми
використання
ресурсів на
виготовлення
одиниці
нерентабельної
продукції
для зміни
асортименту
виробництва.
для
тих видів
продукції,
виробництво
яких за
оптимальним
планом є
недоцільним.
З першого
погляду
здається, що
таке дослідження
є
беззмістовним.
Однак
виконані
розрахунки
містять додаткову
інформацію,
яку можна
використати
для
прийняття
управлінських
рішень у виробництві,
приміром
визначити, у
який спосіб
необхідно
змінити
норми
використання
ресурсів на
виготовлення
одиниці
нерентабельної
продукції
для зміни
асортименту
виробництва.
Перехід
до двоїстої
задачі не
обов’язковий.
Легко
помітити, що
звичайна
симплексна
таблиця в
стовпчиках
містить
початкову
задачу, а в
рядках —
двоїсту. Оцінками
плану прямої
задачі є рядок
![]() (
(![]() ), а
оцінками
плану
двоїстої —
стовпчик
«План» з
компонентами
вектора
вільних
членів системи
обмежень В. Отже,
розв’язуючи
пряму задачу,
симплексний
метод дає
змогу
одночасно
знаходити і
розв’язок
двоїстої
задачі. Однак
двоїсту задачу
можна також
розв’язати за
таблицею, в
якій записана
пряма, а
відшукавши
оптимальний
план двоїстої
задачі, разом
з тим
отримати
розв’язок
початкової
задачі. Такий
спосіб
розв’язання
задачі лінійного
програмування
має назву двоїстого
симплексного
методу.
Прямий та
двоїстий
симплексні
методи пов’язані
між собою.
), а
оцінками
плану
двоїстої —
стовпчик
«План» з
компонентами
вектора
вільних
членів системи
обмежень В. Отже,
розв’язуючи
пряму задачу,
симплексний
метод дає
змогу
одночасно
знаходити і
розв’язок
двоїстої
задачі. Однак
двоїсту задачу
можна також
розв’язати за
таблицею, в
якій записана
пряма, а
відшукавши
оптимальний
план двоїстої
задачі, разом
з тим
отримати
розв’язок
початкової
задачі. Такий
спосіб
розв’язання
задачі лінійного
програмування
має назву двоїстого
симплексного
методу.
Прямий та
двоїстий
симплексні
методи пов’язані
між собою.
![]() , (3.60)
, (3.60)
![]() , (3.61)
, (3.61)
![]() . (3.62)
. (3.62)
![]() (3.63)
(3.63)
![]() . (3.64)
. (3.64)
Допустимо,
що
початковий
базис
складається
з m
векторів ![]() , причому
хоча б одна з
компонент
вектора
, причому
хоча б одна з
компонент
вектора ![]() від’ємна.
Нехай
від’ємна.
Нехай ![]() , однак
справджується
критерій
оптимальності
плану, тобто
всі оцінки
векторів
, однак
справджується
критерій
оптимальності
плану, тобто
всі оцінки
векторів ![]() (
(![]() ). На
підставі
першої
теореми
двоїстості
план
двоїстої
задачі
відшукуємо у
вигляді:
). На
підставі
першої
теореми
двоїстості
план
двоїстої
задачі
відшукуємо у
вигляді: ![]() . Цей план
не є
оптимальним
для прямої
задачі,
оскільки він
не задовольняє
умову
невід’ємності
змінних (3.62) і не
є оптимальним
для двоїстої
задачі, бо
всі оцінки векторів
оптимального
плану двоїстої
задачі мають
бути
невід’ємними.
. Цей план
не є
оптимальним
для прямої
задачі,
оскільки він
не задовольняє
умову
невід’ємності
змінних (3.62) і не
є оптимальним
для двоїстої
задачі, бо
всі оцінки векторів
оптимального
плану двоїстої
задачі мають
бути
невід’ємними.
Отже,
вектор, що
відповідає
компоненті ![]() , потрібно
виключити з
базису
початкової
задачі, а
вектор
двоїстої
задачі, що
відповідає
від’ємній
оцінці,
включити до
базису
двоїстої.
, потрібно
виключити з
базису
початкової
задачі, а
вектор
двоїстої
задачі, що
відповідає
від’ємній
оцінці,
включити до
базису
двоїстої.
£», ввести додаткові
невід’ємні
змінні,
визначити
початковий
базис та перший
опорний план ![]() .
.
2. Якщо
всі оцінки
векторів ![]() і
компоненти
вектора-стовпчика
«План»
і
компоненти
вектора-стовпчика
«План» ![]() для
всіх
для
всіх ![]() , то задача
розв’язана.
Інакше
необхідно
вибрати найбільшу
за модулем
компоненту
, то задача
розв’язана.
Інакше
необхідно
вибрати найбільшу
за модулем
компоненту ![]() і
відповідну
змінну
і
відповідну
змінну ![]() виключити
з базису.
виключити
з базису.
3. Якщо
в l-му
рядку, що
відповідає
змінній ![]() , не
міститься
жодного
, не
міститься
жодного ![]() , то
цільова
функція
двоїстої
задачі необмежена
на
багатограннику
розв’язків, а
початкова
задача
розв’язку не
має. Інакше
існують
деякі
, то
цільова
функція
двоїстої
задачі необмежена
на
багатограннику
розв’язків, а
початкова
задача
розв’язку не
має. Інакше
існують
деякі ![]() і
тоді для
відповідних
стовпчиків визначають
аналогічно
прямому
симплекс-методу
оцінки
і
тоді для
відповідних
стовпчиків визначають
аналогічно
прямому
симплекс-методу
оцінки ![]() :
:
![]() (
(![]() ),
),
Зазначимо,
що для задачі
знаходження
максимального
значення
цільової
функції за
наведеним
алгоритмом
необхідно
перейти до
цільової
функції ![]() , або дещо
змінити сам
алгоритм.
, або дещо
змінити сам
алгоритм.

![]()
![]()
![]() .
.
![]()
![]() .
.
Початковий
базис —
вектори А4
та А5.
Псевдоплан ![]() .
.
|
x |
x |
x |
x |
x |
|||
|
| |||||||
|
Fj – cj £ | |||||||
Оскільки ![]() , то з
базису
необхідно
вивести
вектор А5
і відповідну
змінну
, то з
базису
необхідно
вивести
вектор А5
і відповідну
змінну ![]() .
.
Для
визначення
вектора, що
вводиться в
базис,
розрахуємо
значення ![]() . В другому
рядку
містяться
два від’ємних
коефіцієнти
. В другому
рядку
містяться
два від’ємних
коефіцієнти ![]()
![]() , які
відповідають
векторам А1 та А3. Визначимо,
який з цих
векторів
необхідно
вводити в базис.
, які
відповідають
векторам А1 та А3. Визначимо,
який з цих
векторів
необхідно
вводити в базис.
![]() .
.
Отже,
![]() , значить, у
базис слід
ввести
вектор А1.
Розв’язувальним
елементом
буде а21
(–1).
, значить, у
базис слід
ввести
вектор А1.
Розв’язувальним
елементом
буде а21
(–1).
|
| |||||||
|
Fj – cj £ | |||||||
|
x x | |||||||
|
Fj – cj £ | |||||||
![]() ,
, ![]()
![]() ,
, ![]() .
.
Для
розрахунку
оптимального
плану двоїстої
задачі
необхідно
було
значення
оцінок ![]() домножити
на (– 1), оскільки
ці спряжені задачі
є
симетричними.
домножити
на (– 1), оскільки
ці спряжені задачі
є
симетричними.
Розглянемо задачу лінійного програмування у разі лінійної залежності компонентів вектора обмежень від параметра t. Нехай:
![]() ,
, ![]() ,
, ![]() . (3.65)
. (3.65)
![]() (3.66)
(3.66)
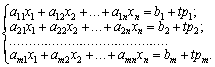 (3.67)
(3.67)
![]()
![]() . (3.68)
. (3.68)
Очевидно,
що для кожного
фіксованого
значення ![]() задача
(3.66)—(3.68) є
звичайною
задачею
лінійного
програмування
і може бути
розв’язана
симплексним
методом.
задача
(3.66)—(3.68) є
звичайною
задачею
лінійного
програмування
і може бути
розв’язана
симплексним
методом.
У разі
визначення
розв’язку
задачі,
придатного
для
довільного
можливого
значення параметра
![]() , потрібні
розв’язки
іноді
вдається
знаходити за
допомогою
дещо
видозміненого
алгоритму
симплексного
методу.
, потрібні
розв’язки
іноді
вдається
знаходити за
допомогою
дещо
видозміненого
алгоритму
симплексного
методу.
Нехай
![]() . Тоді
згідно з
першою
теоремою
двоїстості оптимальний
план прямої
задачі (як і
кожен поточний
опорний план)
можна подати
у вигляді:
. Тоді
згідно з
першою
теоремою
двоїстості оптимальний
план прямої
задачі (як і
кожен поточний
опорний план)
можна подати
у вигляді:
![]() , (3.69)
, (3.69)
де D
— матриця, що
складена з
компонент
векторів
останнього
базису; ![]() —
оптимальний
план задачі
(3.66)—(3.68); В —
вектор, що
складається
з вільних
членів системи
обмежень в
останній симплексній
таблиці.
—
оптимальний
план задачі
(3.66)—(3.68); В —
вектор, що
складається
з вільних
членів системи
обмежень в
останній симплексній
таблиці.
Отже,
якщо
змінюються
компоненти
вектора В, то
змінюються
також
значення
вектора ![]() . У
векторній
формі (3.65) має
вигляд:
. У
векторній
формі (3.65) має
вигляд:
![]() , (3.70)
, (3.70)
де В — вектор з компонентами bi, а вектор Р складається з компонент рі виразу (3.65). Використовуючи (3.69), маємо:
![]() . (3.71)
. (3.71)
Добутком
![]() буде
вектор, який
позначимо
через
буде
вектор, який
позначимо
через ![]() , а результатом
множення
, а результатом
множення ![]() на
на ![]() —
вектор
—
вектор ![]() , тоді:
, тоді:
![]() . (3.72)
. (3.72)
|
|
|
cm+1 |
cn |
|||||||
|
x1 |
xm+1 |
xn |
||||||||
|
x1 |
|
|
|
a11 |
|
|
||||
|
x2 |
|
|
|
a21 |
|
|
||||
|
m |
xm |
сm |
|
|
|
am1 |
|
|
||
|
m + 1 |
Fj – cj ³ |
|
|
|
|
|
|
|||
Таблиця
містить два
додаткових
стовпчики, що
дає змогу стежити
за
перетвореннями
величин ![]() після
здійснених
ітерацій.
після
здійснених
ітерацій.
Оскільки
таблиця 3.5
містить за
допущенням
оптимальний
план задачі
(3.66)—(3.68) ![]() , то має
виконуватися
умова невід’ємності
всіх
компонент
вектора (3.72),
отже,
, то має
виконуватися
умова невід’ємності
всіх
компонент
вектора (3.72),
отже,
![]() (3.73)
(3.73)
Допустимо тепер, що у формулі (3.73) параметр t0 не фіксований, а може набувати довільних значень на заданому інтервалі [а; b]. Якщо для всіх цих значень параметра нерівності (3.73) задовольняються, тобто
![]() , (3.74)
, (3.74)
то це
означає, що
знайдений
план ![]() оптимальний
для всіх значень
оптимальний
для всіх значень
![]() і є
розв’язком
параметричної
задачі (3.66)—(3.68).
Проте в
загальному
випадку
нехай за певних
значень
і є
розв’язком
параметричної
задачі (3.66)—(3.68).
Проте в
загальному
випадку
нехай за певних
значень ![]() нерівності
(3.73) не
задовольняються
і план
нерівності
(3.73) не
задовольняються
і план ![]() уже
не буде оптимальним.
Тому
необхідно
виявити множину
всіх значень
уже
не буде оптимальним.
Тому
необхідно
виявити множину
всіх значень ![]() (де
проміжок [а0; b0]
менший, ніж [а; b]), для яких
знайдений
план є
оптимальним,
і, виключивши
її з
подальшого
розгляду,
знаходити
оптимальний
план для
другої
множини точок
з інтервалу
(де
проміжок [а0; b0]
менший, ніж [а; b]), для яких
знайдений
план є
оптимальним,
і, виключивши
її з
подальшого
розгляду,
знаходити
оптимальний
план для
другої
множини точок
з інтервалу ![]() і т.
д. Отже,
процес
розв’язання
параметричної
задачі
передбачає
послідовний
поділ заданого
проміжку
і т.
д. Отже,
процес
розв’язання
параметричної
задачі
передбачає
послідовний
поділ заданого
проміжку ![]() зміни
параметра t на ряд
таких
підпроміжків,
щоб для всіх
значень
зміни
параметра t на ряд
таких
підпроміжків,
щоб для всіх
значень ![]() того
самого
підпроміжку
оптимум цільової
функції
досягався в
одній точці
(вершині)
багатогранника
планів задачі,
але щоб
кожному
підпроміжку
зміни параметра
відповідав
окремий оптимальний
план.
того
самого
підпроміжку
оптимум цільової
функції
досягався в
одній точці
(вершині)
багатогранника
планів задачі,
але щоб
кожному
підпроміжку
зміни параметра
відповідав
окремий оптимальний
план.
Отже,
розв’язування
параметричної
задачі (3.66)—(3.68) починають
з деякого
значення ![]() і
записують задачу
(3.66)—(3.68) у вигляді
початкової
симплексної
таблиці, що
має вигляд,
аналогічний
таблиці 3.5.
Знаходять
симплексним
методом оптимальний
план задачі
(якщо він
існує) для даного
значення
параметра
(таблиця 3.5).
Зазначимо, що
значення
компонент
оптимального
плану
подається у
вигляді двох доданків,
що містяться
в двох
додаткових
стовпчиках
і
записують задачу
(3.66)—(3.68) у вигляді
початкової
симплексної
таблиці, що
має вигляд,
аналогічний
таблиці 3.5.
Знаходять
симплексним
методом оптимальний
план задачі
(якщо він
існує) для даного
значення
параметра
(таблиця 3.5).
Зазначимо, що
значення
компонент
оптимального
плану
подається у
вигляді двох доданків,
що містяться
в двох
додаткових
стовпчиках ![]() та
та ![]() . Загальні
значення
цільової
функції
оптимального
плану
розраховують
додаванням
до суми
стовпця
. Загальні
значення
цільової
функції
оптимального
плану
розраховують
додаванням
до суми
стовпця ![]() суми
стовпця
суми
стовпця ![]() ,
помноженої
на
,
помноженої
на ![]() (згідно
з 3.72). Отже,
величина
(згідно
з 3.72). Отже,
величина ![]() є
лінійною
функцією
параметра t.
є
лінійною
функцією
параметра t.
Визначимо
границі
значень
параметра t,
для яких
вектор ![]() буде
оптимальним
планом. Для
цього з
остаточної
таблиці 3.5, де
буде
оптимальним
планом. Для
цього з
остаточної
таблиці 3.5, де ![]() ,
складаємо і
розв’язуємо
систему
нерівностей
(3.74). У разі
існування
оптимального
плану задачі
при
,
складаємо і
розв’язуємо
систему
нерівностей
(3.74). У разі
існування
оптимального
плану задачі
при ![]() система
нерівностей
(3.74), очевидно,
сумісна,
оскільки
існує хоча б
один її розв’язок.
Зрозуміло
також, що
обов’язково
деякі з
система
нерівностей
(3.74), очевидно,
сумісна,
оскільки
існує хоча б
один її розв’язок.
Зрозуміло
також, що
обов’язково
деякі з ![]() , бо інакше
параметричної
задачі не
було б. Слід
розрізняти
два випадки
при
розв’язанні
системи
нерівностей
(3.74):
, бо інакше
параметричної
задачі не
було б. Слід
розрізняти
два випадки
при
розв’язанні
системи
нерівностей
(3.74):
а) Якщо
існують такі
значення і, для
яких ![]() , тоді
розв’язками
відповідних
нерівностей
будуть:
, тоді
розв’язками
відповідних
нерівностей
будуть:
![]() , (3.75)
, (3.75)
Якщо
немає ![]() , тобто всі
, тобто всі ![]() , то
значення t, для яких
знайдений
план
, то
значення t, для яких
знайдений
план ![]() буде
оптимальним,
знизу не
обмежені,
тобто
буде
оптимальним,
знизу не
обмежені,
тобто ![]() .
.
б) Якщо
існують такі
значення і, для
яких ![]() , то розв’язками
відповідних
нерівностей
будуть:
, то розв’язками
відповідних
нерівностей
будуть:
![]() . (3.76)
. (3.76)
В такому
разі
розв’язок
системи
нерівностей
дає верхню границю
шуканого
інтервалу,
яка може
дорівнювати
або бути більшою
за а (![]() ). Якщо
немає
). Якщо
немає ![]() , тобто всі
, тобто всі ![]() , то сукупність
значень t, для яких
знайдений план
, то сукупність
значень t, для яких
знайдений план
![]() буде
оптимальним,
зверху
необмежена (
буде
оптимальним,
зверху
необмежена (![]() ), і в цьому
останньому
разі задача
розв’язана повністю,
оскільки
), і в цьому
останньому
разі задача
розв’язана повністю,
оскільки
![]() .
.
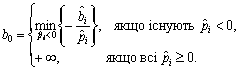 (3.77)
(3.77)
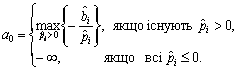 (3.78)
(3.78)
За
найменшого
виходу
величини t за межі
визначеного
інтервалу [a0; b0]
значення
нового
оптимального
плану ![]() буде
від’ємним
(порушуватимуться
умови системи
нерівностей
(3.74)).
буде
від’ємним
(порушуватимуться
умови системи
нерівностей
(3.74)).
Тобто
(3.74) визначає
вектор, який
необхідно вивести
з базису.
Припустимо,
що за деякого
![]() , де
, де ![]() ,
мінімальне
значення в (3.77),
яке визначає
верхню
границю інтервалу
,
мінімальне
значення в (3.77),
яке визначає
верхню
границю інтервалу
![]() , досягається
для
, досягається
для ![]() . Отже,
порушується k-та
нерівність
із (3.74), і з
базису
необхідно
виводити
вектор, що
відповідає
змінній
. Отже,
порушується k-та
нерівність
із (3.74), і з
базису
необхідно
виводити
вектор, що
відповідає
змінній ![]() . Тому при
. Тому при ![]() необхідно
здійснити
зміну базису,
для чого виконують
один крок двоїстого
симплекс-методу,
розглянутого
в § 3.6., і
визначають
нове
значення
необхідно
здійснити
зміну базису,
для чого виконують
один крок двоїстого
симплекс-методу,
розглянутого
в § 3.6., і
визначають
нове
значення ![]() .
.
Далі
розглядають
знову
систему
нерівностей
(3.74). Для ![]() за
формулою (3.77)
визначають
верхню границю
за
формулою (3.77)
визначають
верхню границю
![]() тих
значень t, для яких
відшуканий
план
тих
значень t, для яких
відшуканий
план ![]() буде
оптимальним.
Таку
процедуру
повторюють
доти, поки не
отримають
значення
верхньої
границі
чергового
інтервалу, що
дорівнює або
перевищує
верхню
границю
заданого
інтервалу
буде
оптимальним.
Таку
процедуру
повторюють
доти, поки не
отримають
значення
верхньої
границі
чергового
інтервалу, що
дорівнює або
перевищує
верхню
границю
заданого
інтервалу ![]() можливих
значень t, тобто
можливих
значень t, тобто
![]() . (3.79)
. (3.79)
Отже, заданий проміжок [a; b] поділяють на ряд інтервалів [a; b0], [b1; b2], … [bs–1; b], для кожного з яких максимум цільової функції досягається за відповідного йому одного оптимального плану.
![]() (3.80)
(3.80)
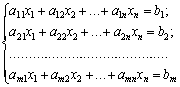 (3.81)
(3.81)
![]() (3.82)
(3.82)
![]() . (3.83)
. (3.83)
![]() (3.84)
(3.84)
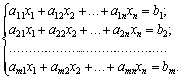 (3.85)
(3.85)
![]()
![]() . (3.86)
. (3.86)
За
деякого
фіксованого
значення ![]() задача
(3.84)—(3.86)
перетворюється
в звичайну
задачу
лінійного
програмування.
Зміни
коефіцієнтів
цільової
функції в
процесі
реалізації
симплексного
методу
впливатимуть
на значення
оцінкового
ряду (
задача
(3.84)—(3.86)
перетворюється
в звичайну
задачу
лінійного
програмування.
Зміни
коефіцієнтів
цільової
функції в
процесі
реалізації
симплексного
методу
впливатимуть
на значення
оцінкового
ряду (![]() ).
).
![]() .
.
![]()
![]()
Позначимо
перетворені
методом
повних виключень
Жордана—Гаусса
в процесі
перерахунку
початкової
симплексної
таблиці ![]() через
через ![]() ,
аналогічно
,
аналогічно ![]() — як
— як ![]() . Остання
симплексна
таблиця
набуде такого
вигляду:
. Остання
симплексна
таблиця
набуде такого
вигляду:
|
+ t0 p1 |
cm + t0 pm |
cn + t0 pn |
||||||
|
x |
xm |
xn |
||||||
|
x |
+ t0 p1 |
|
a |
|
|
|||
|
x |
+ t0 p2 |
|
a |
|
|
|||
|
m |
xm |
cm + t0 pm |
|
am |
|
|
||
|
m |
|
|
|
|
|
|||
|
m |
|
|
|
|
|
|||
|
m |
Fj – cj ³ |
|
|
|
|
|||
Таблиця
(аналогічно
випадку
параметричної
зміни
вектора
обмежень
—табл. 3.5)
містить два
додаткових
рядки, що дає
змогу
стежити за
перетвореннями
величин ![]() після
кожної
ітерації.
після
кожної
ітерації.
1. Слід
зафіксувати
деяке
значення ![]() і
розв’язати задачу
(3.84)—(3.86) як
звичайну
задачу
лінійного
програмування
симплексним
методом.
і
розв’язати задачу
(3.84)—(3.86) як
звичайну
задачу
лінійного
програмування
симплексним
методом.
2.
Оптимальний
план з
останньої
симплексної
таблиці 3.6 є сумою
двох
доданків,
значення
яких
знаходяться
в рядках ![]() та
та ![]() , причому
має
виконуватися
умова
невід’ємності
всіх
компонент век
, причому
має
виконуватися
умова
невід’ємності
всіх
компонент век
![]() .
.
3.
Встановлюємо
границі
значень
параметра t, для
яких вектор ![]() залишатиметься
оптимальним
планом. Для
цього з
останньої
симплексної
таблиці
складаємо
систему
нерівностей
залишатиметься
оптимальним
планом. Для
цього з
останньої
симплексної
таблиці
складаємо
систему
нерівностей
![]() . (3.87)
. (3.87)
а) Якщо
існують такі
значення j, для яких ![]() , тоді
розв’язками
відповідних
нерівностей
будуть:
, тоді
розв’язками
відповідних
нерівностей
будуть:
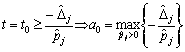 . (3.88)
. (3.88)
У
такий спосіб
визначають
нижню
границю шуканого
інтервалу,
яка може
дорівнювати а або
бути меншою
за неї: ![]() .
.
Якщо
немає ![]() , тобто всі
, тобто всі ![]() , то
значення t,
для яких знайдений
, то
значення t,
для яких знайдений
![]() буде
оптимальним,
знизу не
обмежені,
тобто
буде
оптимальним,
знизу не
обмежені,
тобто ![]() .
.
б) Якщо
існують такі
значення і, для яких ![]() , то
розв’язками
відповідних
нерівностей
будуть:
, то
розв’язками
відповідних
нерівностей
будуть:
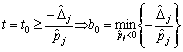 . (3.89)
. (3.89)
З
цих
розв’язків
визначають
верхню
границю
шуканого
інтервалу,
яка може
дорівнювати
або бути
більшою за а (![]() ). Якщо немає
). Якщо немає
![]() , тобто всі
, тобто всі ![]() , то
сукупність
значень t, для яких
знайдений
план
, то
сукупність
значень t, для яких
знайдений
план ![]() буде
оптимальним,
зверху
необмежена (
буде
оптимальним,
зверху
необмежена (![]() ) і в цьому
останньому
випадку
задача розв’язана
повністю,
оскільки
) і в цьому
останньому
випадку
задача розв’язана
повністю,
оскільки
![]() .
.
4.
Система (3.74)
визначає
вектор, який
необхідно вивести
з базису. Припустимо,
що за деякого
![]() , де
, де ![]() , мінімальне
значення в (3.89),
яке визначає
верхню границю
інтервалу
, мінімальне
значення в (3.89),
яке визначає
верхню границю
інтервалу ![]() ,
досягається
для
,
досягається
для ![]() . Отже,
порушується k-та
нерівність
із (3.87), і з
базису
необхідно виводити
вектор, що
відповідає
змінній
. Отже,
порушується k-та
нерівність
із (3.87), і з
базису
необхідно виводити
вектор, що
відповідає
змінній ![]() . Тому при
. Тому при ![]() необхідно
провести
замі 838h73i ну
базису, для
чого
виконують
один крок
двоїстого
симплекс-методу,
розглянутого
в 3.6, і
визначають
нове значення
необхідно
провести
замі 838h73i ну
базису, для
чого
виконують
один крок
двоїстого
симплекс-методу,
розглянутого
в 3.6, і
визначають
нове значення
![]() .
.
5.
Розглядаємо
знову
систему
нерівностей
(3.87). Для ![]() за
формулою (3.77)
визначаємо
верхню границю
за
формулою (3.77)
визначаємо
верхню границю
![]() тих
значень t, для яких
відшуканий
план
тих
значень t, для яких
відшуканий
план ![]() буде
оптимальним.
буде
оптимальним.
6.
Процедуру
повторюємо
доти, поки не
отримаємо
значення верхньої
границі
чергового
інтервалу, що
дорівнює або
перевищує
верхню
границю заданого
інтервалу ![]() можливих
значень t, тобто
можливих
значень t, тобто
![]() . (3.90)
. (3.90)
Отже,
заданий
проміжок ![]() поділяють
на ряд
інтервалів
поділяють
на ряд
інтервалів ![]() , для
кожного з
яких
максимум
цільової функції
досягається
за
відповідного
йому одного
оптимального
плану.
, для
кожного з
яких
максимум
цільової функції
досягається
за
відповідного
йому одного
оптимального
плану.

![]()
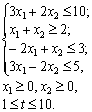
Нехай
![]() .
Розв’яжемо
задачу
модифікованим
симплексним методом,
використовуючи
таблицю з
двома додатковими
рядками.
.
Розв’яжемо
задачу
модифікованим
симплексним методом,
використовуючи
таблицю з
двома додатковими
рядками.
|
x |
x |
x |
x |
x |
x | ||||
|
x | |||||||||
|
x | |||||||||
|
| |||||||||
|
x | |||||||||
|
D j | |||||||||
|
pj | |||||||||
|
Fj – cj ³ | |||||||||
|
| |||||||||
|
x | |||||||||
|
x | |||||||||
|
x | |||||||||
|
D j | |||||||||
|
pj | |||||||||
|
Fj – cj ³ | |||||||||
|
x | |||||||||
|
x | |||||||||
|
x | |||||||||
|
x | |||||||||
|
D j | |||||||||
|
pj | |||||||||
|
Fj – cj ³ | |||||||||
Остання
симплексна
таблиця
містить перший
оптимальний
план задачі ![]()
Верхня
границя
першого
проміжку
згідно з (3.89)
дорівнює ![]() . Отже, на
інтервалі
. Отже, на
інтервалі ![]() план
план ![]() буде оптимальним,
причому
оптимальне
значення
цільової
функції буде
такою лінійною
функцією
параметра t:
буде оптимальним,
причому
оптимальне
значення
цільової
функції буде
такою лінійною
функцією
параметра t:
![]()
і при ![]()
![]() .
.
Оскільки
при ![]() елемент
m + 2
рядка та
п’ятої
колонки буде
нульовим,
беремо п’яту
колонку за
розв’язувальну
і, відкинувши
m + 2
рядок,
здійснюємо
одну
ітерацію.
Отримаємо
таку таблицю:
елемент
m + 2
рядка та
п’ятої
колонки буде
нульовим,
беремо п’яту
колонку за
розв’язувальну
і, відкинувши
m + 2
рядок,
здійснюємо
одну
ітерацію.
Отримаємо
таку таблицю:
|
Δj | ||||||||
|
pj | ||||||||
В m + 3
рядку цієї
таблиці
немає
від’ємних
елементів, а
тому згідно з
формулою (3.89)
знайдений план
![]() буде
оптимальним
для всіх
значень t, що лежать
на інтервалі
буде
оптимальним
для всіх
значень t, що лежать
на інтервалі ![]() .
Оптимальне
значення
цільової
функції є такою
лінійною
функцією параметра
t:
.
Оптимальне
значення
цільової
функції є такою
лінійною
функцією параметра
t:
![]() .
.
При
![]()
![]() .
.
![]()
![]()
![]()
mах z = –30x1 + 10x2;
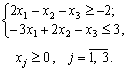
min z = 4x1 + 3x2 + x3;
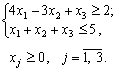
max z = 3x1 + 2x2 + 5x3;
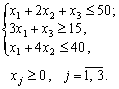
|