ALTE DOCUMENTE
|
|||||||||
INDICI TOPOLOGICI SI TOPOGRAFICI
3.1. Generalitati
Matricile prezentate in Capitolul 2 reprezinta invarianti topologici care reprezinta sursa de obtinere a unor numere sau seturi de numere care codeaza informatia structurala ce caracterizeaza un graf chimic.
Aceste numere reprezinta tocmai indicii topologici care exprima numeric informatia topologica continuta in graful molecular sau constitutional. De-a lungul timpului o preocupare majora in literatura de specialitate a fost studierea reducerii grafurilor sau a matricilor prezentate in Capitolul 2 la indici topologici/topografici [14, 23, 48, 124].
O prima metoda consta in estimarea valorilor proprii ale determinantilor asociati matricilor respective, T, conform relatiei de mai jos in care E reprezinta matricea unitate, X este variabila iar n este numarul de varfuri din graful initial.
![]()
Ecuatia 62 conduce la polinomul caracteristic P(X) [125]. Cercetarile ulterioare au aratat ca spectrul de valori proprii nu este insa unic si ca fiecare graf arborescent isi are perechea sa izospectrala [126] si din aceasta cauza s-au dezvoltat alte metode care se bazeaza pe descompunerea grafului [127], la indici topologici centrici (Balaban) [128] precum si la aplicarea teoriei informationale pentru caracterizarea cantitativa a structurii.
Indicii topologici (TI) reprezinta asadar o unealta importanta pentru studiile QSAR /QSPR. In functie de dezvoltarea lor istorica acestia pot fi clasificati in trei generatii iar in functie de natura descriptorului local sau global in numere intregi sau reale [129].
3.2. Prima generatie de indici topologici
Acest tip de indici topologici (TI) sunt numere intregi precum si invariantii locali ai varfurilor grafurilor (LOVI) din care se pot construi astfel de indici topologici.
3.2.1. Indicele Wiener
Primul descriptor a fost introdus in topologia moleculara in anul 1947 de catre H. Wiener [130]. Pentru a corela punctele de fierbere sau alte proprietati ale alcanilor cu structura lor Wiener propune urmatoarea ecuatie liniara:
tB = a·w + b·p + c (63)
unde a, b si c sunt constante pentru un set de izomeri iar p si w sunt variabile structurale care vor fi definite in cele ce urmeaza.
p reprezinta polaritatea si este definita ca numarul perechilor atomilor de carbon care sunt separate prin trei legaturi C-C. In Figura 40 sunt prezentate formula moleculara (a) si graful corespunzator (b) pentru 2, 3-dimetil-pentan.
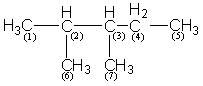
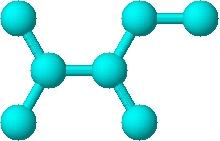
40a 40b
Figura 40. Formula moleculara (40a) si graful corespunzator (40b) pentru 2,3-dimetil-pentan.
Din Figura 1a, 1b se observa 6 perechi de atomi de carbon separate prin trei legaturi C-C : C1C4 ; C1C7 ; C2C5 ; C4C6 ; C5C7 ; C6C7 asadar polaritatea p = 6.
Pentru a defini parametrul w [50, 111, 128-131] care mai tarziu in literature de specialitate va fi numit indicele Wiener se considera un graf G indirect conectat care are varfurile 1, 2,.n. Pentru graful G varfurile i0, i1, ..,ik sunt k+1 varfuri distincte si pentru j = 1, 2, ..,k, ij-1 si ij sunt adiacente. Varfurile i0, i1, ..,ik formeaza o cale in graful G de lungime k. Lungimea celei mai scurte cai dintre varfurile conectate x si y se noteaza Dxy. Distanta este astfel aleasa incat sunt valabile imediat relatiile : Dxy=0 daca si numai daca x=y ; Dxy= Dyx si Dxy+ Dyx Dxz. Suma distantelor dintre toate perechile de varfuri reprezinta indicele Wiener We.
![]()
In Figura 41 sunt prezentate formula moleculara (41a) si graful corespunzator (41b) pentru 1, 3-dimetil-ciclooctan.
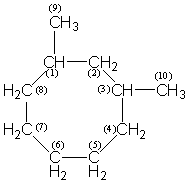
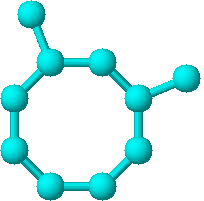
a b
Figura 41 Formula moleculara (41a) si graful corespunzator (41b) pentru 1, 3-dimetil-ciclooctan.
Pentru graful G10 prezentat in Figura 41 (41b) distantele Dxy sunt :
D12 = 1 D13 = 2 D14 = 3 D15 = 4 D16 = 3 D17 = 2 D18 = 1 D19 = 1 D110 = 4
D23 = 1 D24 = 2 D25 = 3 D26 = 4 D27 = 3 D28 = 2 D29 = 2 D210 = 3
D34 = 1 D35 = 2 D36 = 3 D37 = 4 D38 = 3 D39 = 3 D310 = 1
D45 = 1 D46 = 2 D47 = 3 D48 = 4 D49 = 4 D410 = 2
D56 = 1 D57 = 2 D58 = 3 D59 = 5 D510 = 3
D67 = 1 D68 = 2 D69 = 4 D610 = 4
D78 = 1 D79 = 3 D710 = 5
D89 = 2 D810 = 4
D910 = 4
Numerele Dxy, x=1,2,..,N, y=1,2,..,N definesc patratul unei matrici simetrice de ordinul N uzual notata cu De. Indicele Wiener este egal cu suma distantelor intre toate perechile de varfuri ale grafului respectiv : We=We(G)= x<yDxy.
We(G10) =(1+2+3+4+3+2+1+1+4)+(1+2+3+4+3+2+2+3)+(1+2+3+4+3+3+1)+(1+2+3+4
Un numar de indici topologici noi a fost construit ca extensie la indicele Wiener [132-134]. Preocupari majore privind extensii la indicele Wiener apartin lui Gutman [135] sau Klein si Randic care introduc conceptul de distanta-rezistenta [112] concept care a fost detaliat in Subcapitolul 2.9.
3.2.1.1. Indicele Wiener general, model de caracterizare moleculara topologica a hidrocarburilor saturate sau nesaturate
Indicele Wiener general reprezinta o unealta importanta pentru caracterizarea avansata a structurilor compusilor chimici. Pentru definirea sa se considera K(G) subgrafuri apartinand unui graf G ce formeaza serii de clase de ordinul e cu e = 1, 2, ..,E. e reprezinta numarul de muchii pentru orice subgraf din fiecare clasa fiind un numar constant iar E reprezinta numarul de muchii(numar constant) din intregul graf G.
Definitia 1: Numarul Wiener general OW(G) pentru orice graf G este definit [134] ca suma a numerelor Wiener (indicilor) Wi(Gi) pentru toate subgrafurile K ale grafului G.
![]()
Definitia 2: Numarul Wiener general de ordinul ,,e'' eOW(G) pentru orice graf G este definit [134] ca suma a numerelor Wiener Wj( eGj ) pentru toate subgrafurile eK, eG G, care au e muchii:
![]()
Definitia 3: Numarul Wiener general de ordinul ,,e'' eOW(G) poate fi definit [134] ca suma a termenilor eOWk(G) reprezentand suma numerelor Wiener in tipurile de subgrafuri specificate. Distantele in cazul grafurilor aciclice sunt k=p, pentru clustere k=c iar pentru ,,clustere carare'' k=pc, fiind definite de Kier si Hall [48]:

Definitia 4: Vectorul numar Wiener general OW'(G) pentru orice graf G este reprezentat de secventa tuturor eOW(G) in ordine crescatoare a numarului de muchii e [134]:
OW'(G) = OW (68)
iar pentru grafurile aciclice:
OW'(G) = OW (69)
Din Definitia 2 rezulta urmatoarele corolare:
Corolarul 1: Numarul Wiener general de ordinul E (EOW(G)) este chiar indicele Wiener insusi :
EOW(G) = W (70)
Corolarul 2: Numarul Wiener general de ordinul 0 (0OW(G)) este egal cu 0:
OW(G) = 0 (71)
Corolarul 3: Numarul Wiener general de ordinul 1 (1OW(G)) este egal cu numarul de muchii E din graf:
OW(G) = E (72)
3.2.1.2. Formulele numarului Wiener general pentru mai multe clase de grafuri
Pentru un graf G se noteaza cu n numarul de varfuri, cu E numarul de muchii iar pentru un subgraf se noteaza cu e numarul de muchii in timp ce numarul de sugrafuri avand e muchii se noteaza cu eK.
Notatiile prezentate mai sus au fost utilizate in urmatoarele formulele de calcul ale numarului Wiener general pentru mai multe clase de grafuri:
Grafuri liniare, Pn:
eOW(Pn) = e(e+1)(e+2)(n-e) / 6
OW = (n+3)(n+2)(n+1)n(n-1) / 120 (73)
Grafuri monociclice, Cn:
eOW(Cn) = e(e+1)(e+2)n / 6 (pentru e = 1,2,...,n-1)
EOW(Cn) = W(Cn)
OW(Cn) = (n5 + 2n4 + 2n3 - 2n2 -an) / 24 (74)
a = 0 pentru n = par si a = 3 pentru n = impar
Grafurile Star, Sn
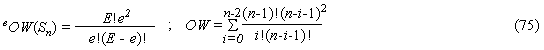
Indicele Wiener general este o masura a doua dintre trasaturile esentiale ale topologiei moleculare: i) ramificarea scheletului molecular; ii) prezenta ciclurilor in aceste schelete moleculare. Valoarea acestui descriptor molecular scade cu cresterea numarului de ramificari, lungimea ramificarii, centralitatea (mai multe pozitii centrale) sau clusterizarea. In cazul grafurilor ciclice, acest descriptor scade cu cresterea numarului de inele din scheletul molecular. Acest tip de indice a fost utilizat in studii QSPR pentru modelarea unor proprietati fizico-chimice ale alcanilor C3-C8 cum ar fi: punctul de fierbere TB [136], temperatura critica TC [136], presiunea critica pc [136], volumul critic Vc [48], volumul molar Vm [48], refractia molara Rm [48], suprafata de tensiune ST [136], caldura de formare in stare gazoasa DHf(g) [137], caldura de vaporizare DHv [137], caldura de atomizare DHa
3.2.1.3. Indicele Wiener general in cazul hidrocarburilor nesaturate
Distanta dintre doua varfuri adiacente in cazul hidrocarburilor nesaturate este diferita de distanta dintre doua varfuri adiacente in cazul hidrocarburilor saturate. In acest caz indicele Wiener general nu mai poate fi aplicat. Pentru ca acest descriptor sa fie aplicat si in cazul hidrocarburilor nesaturate, in anul 2002 Li si Lin definesc un nou concept numit distanta relativa [138] iar noul indice pentru care raman valabile definitiile si corolariile prezentate in Subcapitolul 3.2.1.1. se numeste indicele de valenta Wiener general. Distanta relativa pentru o legatura simpla C-C (de tip sp3-sp3) este egala cu 1 [138] iar pentru alte tipuri de legaturi chimice este definita ca raport al lungimilor legaturilor acestora. Daca lungime legaturii simple C-C(de tip sp3-sp3) este 1.544 atunci distanta relativa pentru o legatura C-C (de tip sp3-sp2) este 1.501/1.544 = 0.972.
In Tabelul 5 sunt prezentate lungimile legaturilor si distantele relative pentru mai multe tipuri de legaturi chimice [138].
|
Legaturi simple C-C |
Tipul |
Lungimea legaturii |
Distanta relativa |
|
|
sp3-sp3 | ||
|
|
sp3-sp2 | ||
|
|
sp3-sp | ||
|
|
sp2-sp2 | ||
|
|
sp2-sp | ||
|
|
sp-sp | ||
|
Legaturi multiple C-C |
Tipul |
Lungimea legaturii |
Distanta relativa |
|
Plumbago |
sp2-sp2+p | ||
|
Benzen |
sp2-sp2+p | ||
|
|
sp2-sp2+p | ||
|
|
sp2-sp+p | ||
|
|
sp-sp+p | ||
|
|
sp-sp+ p |
Tabelul 5. Lungimile legaturilor si distantele relative pentru mai multe tipuri de legaturi chimice [138]
Noul descriptor molecular a fost utilizat in modelari QSPR ale unor proprietati fizice ca punctul de topire in 0C, volumul molecular Vcal in cm3 / mol, coeficientul de partitie logP, refractia molara MR in cm3 / mol, temperatura critica TC in 0C si presiunea critica in atm in cazul unor alchene [136, 138, 139].
3.2.1.4. Indicele Wiener modificat si aplicatiile sale
Asa cum s-a aratat in Subcapitolul 2.2 elementele unei matrici de distante sunt reprezentate de distantele cele mai scurte dintre un atom si alt atom dintr-un graf molecular. In Figura 42 este prezentata forma generala a unei matrici de distante.

Figura 42. Forma generala a unei matrici de distante
Acest tip de matrice reprezinta sursa de constructie a mai multor descriptori topologici printre care si indicele Wiener. In constructia acestui indice [130] se iau in considerare lungimile muchiilor dintre varfurile unui graf (ecuatia 64) dar nu interactiile si proprietatile acestor varfuri.
Dupa cum este bine cunoscut electronegativitatea reprezinta capacitatea atomilor de a ceda sau accepta electroni sau cu alte cuvinte energia de ionizare sau afinitatea electonica a atomilor. Avand in vedere acest fapt, electronegativitatea si distanta dintre atomi a fost utilizata pentru a defini proprietatile si interactiile varfurilor unui graf molecular [140]. In Figura 43 este prezentata noua matrice de distante.

Figura 43. Noua matrice de distante in care intervine electronegativitatea si distanta dintre atomi
in care Ii si Ij sunt valorile electronegativitatii Pauling, Rij reprezinta distanta legaturii dintre varfurile vi si vj .
Daca varfurile vi si vj sunt adiacente atunci Rij se poate obtine in trei moduri: i) valoarea relativa a lungimii legaturii; ii)valoarea relativa a sumei legaturilor covalente; iii)Rij = ni + nj in care ni si nj reprezinta numerele cuantice principale maxime pentru atomii i si j.
Daca varfurile vi si vj nu sunt adiacente atunci Rij reprezinta suma tuturor lungimilor legaturilor atomilor adiacenti de la varful vi la varful vj. a = (Zi / Zj)0.5 unde Zi este numarul atomic pentru atomul pozitiv i iar Zj este numarul atomic pentru atomul negativ j. Pe de alta parte a reprezinta media aritmetica a tuturor valorilor a pentru toate legaturile de la varful vi la varful vj. Acest parametru a masoara diferentele de interactie ale electronilor de la varful vi la varful vj.
In Tabelul 6 sunt prezentati parametrii a, Rij si Dij* pentru mai multe tipuri de legaturi chimice [140].
|
Par. |
C C |
C C |
C C |
C C |
C O |
C O |
C F |
C Cl |
C Br |
C I |
|
a | ||||||||||
|
Rij | ||||||||||
|
Dij* |
Tabelul 6. Parametrii a, Rij si Dij* pentru mai multe tipuri de legaturi chimice [140]
Indicele Wiener modificat a fost utilizat in studii QSPR pentru modelari ale entalpiei de formare DfHmF(kJ mol-1) [141] a metil halogenurilor sau a compusilor anorganici continand metale tranzitionale [140].
3.2.1.5. Alte versiuni ale indicelui Wiener
In decursul ultimilor ani, in literatura de specialitate au fost propusi mai multi invarianti pentru un graf G care reprezinta veriuni ale indicelui Wiener W(G). Un astfel de invariant a fost propus de Lukovits [142] si este prezentat cu ajutorul ecuatiei 76:
![]()
in care pij reprezinta calea dintre varfurile i si j iar |pij| reprezinta lungimea acestei cai.
In cazul grafurilor ciclice a fost propusa matricea W [142] (diferita de matricea distantelor-rezistente) pentru care elementele Wij reprezinta suma lungimilor tuturor cailor dintre varfurile i si j. Luand in considerare elementele acestei matrici, indicele propus de Lukovits se poate prezenta cu ajutorul ecuatiei 77:
![]()
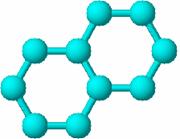
In Figura 44 este prezentat graful molecular (44a), triunghiul superior din matricea W (44b) si valoarea indicelui propus de Lukovits (44c) in cazul naftalinei.

44a 44b
P(naftalina) = 751
44c
Figura 44. Graful molecular (44a), triunghiul superior din matricea W (44b) si valoarea indicelui propus de Lukovits (44c) in cazul naftalinei
Noul indice propus de Lukovits a fost utilizat in studii QSPR pentru modelarea punctelor de fierbere in cazul unor izomeri ciclici si aciclici ai octanului [142].
3.2.1.6. Indicele Wiener in cazul grafurilor benzenoide cata-condensate
Grafurile benzenoide sunt compuse din inele hexagonale. Fiecare din astfel de inele hexagonale sunt adiacente cu alte doua sau trei inele hexagonale cu exceptia inelului hexagonal terminal care este adiacent cu un singur inel hexagonal. Pentru astfel de grafuri a fost propus un indice Wiener mediu [143-145] prezentat in ecuatia 78:
![]()
in care ch reprezinta catene hexagonale cu h hexagoane iar |ch| reprezinta numarul de elemente ch. Indicelui Wiener are valoarea maxima pentru poliacena liniara care reprezinta un sistem de inele hexagonale anelate liniar iar valoarea minima pentru helicena - sistem de inele hexagonale anelate angular [143].
Indicele Wiener mediu pentru o catena hexagonala Rh cu h hexagoane construita cu ajutorul algoritmului propus de Gutman et all. (GKQ) [146] depinde numai de probabilitatile p1, p2 (probabilitatea de adaugare pas cu pas a hexagoanelor terminale) si numarul de hexagoane h din catena hexagonala. Pentru catena hexagonala Rh valoarea asteptata pentru indicele Wiener Wh se poate calcula cu ajutorul ecuatiei 79:
Wh = 4h3 + 16h2 + 6h + 1 + 4/3q(h3 - 3h2 + 2h) - 4/3(p1 - p2)2F(h, q) (79)
q = 1 - p1 - p2
iar pentru h
![]()
unde k reprezinta numarul de pasi urmati pentru a descompune un astfel de graf benzenoid in grafuri mai simple [145].
A. A. Dobrynin demonstreaza [144] ca valoarea pentru Wh este diferita de valoarea medie a indicelui Wiener pentru o catena hexagonala cu h hexagoane Wavg (Jh
Probabilitatea de asamblare a inelelor hexagonale in catena Rh determina mai multe situatii care vor fi analizate in cele ce urmeaza [144]:
Cazul 1: p1 = 1/3, p2 = 1/3 si q = 1/3
In aceasta situatie valoarea |Jh| afost calculata de Balaban si Harary [34] cu ajutorul ecuatiei 81:

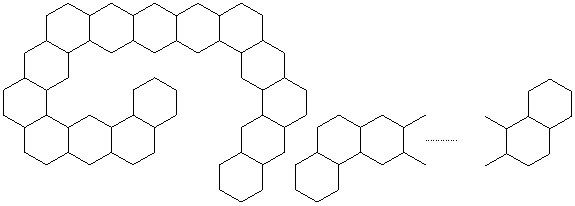
Cazul 2: Pentru graful prezentat in Figura 45 care nu contine subgrafuri Zk (5≤k≤h) caruia ii sunt caracteristici parametrii: p1 = 1/2, p2 = 0 si q = 1/2, valoarea |Jh| se poate calcula cu ajutorul ecuatiei 82 [144].
G Subgrafuri Zk interzise
Figura 45. Graful G caruia ii sunt caracteristici parametrii p1 = 1/2, p2 = 0 si q = 1/2 si subgrafurile Zk interzise
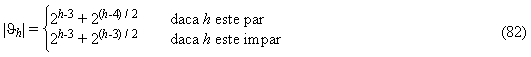
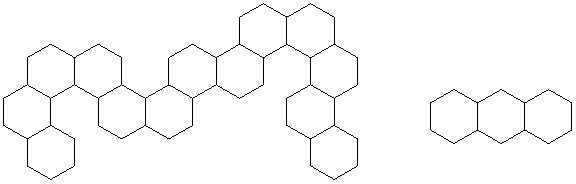
Cazul 3 este caracteristic grafului G care nu contine poliacena liniara L3 caruia ii sunt caracteristici parametrii: p1 = 1/2, p2 = 1/2 si q = 0. In Figura 46 este prezentat graful G la care se face referire impreuna cu subgraful L3 interzis (poliacena liniara).
G L3
Figura 46. Graful G caruia ii sunt caracteristici parametrii p1 = 1/2, p2 = 1/2 si q = 0 si subgraful interzis L3
Valoarea |Jh| se poate calcula cu ajutorul ecuatiei 83 [144]:
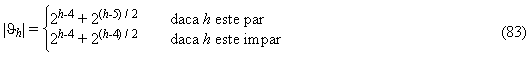
Exista grafuri cum ar fi cele prezentate in Figura 47 pentru care valoarea Wh coincide cu valoarea indicelui Wiener W(G) pentru orice valoare impara a lui h mai mica sau egala cu 15 (3≤h≤15).

G1 G2 G3
Figura 47. Tipuri de grafuri pentru care Wh = W(G)
Valoarea indicelui Wiener W(G) in aceasta situatie se poate calcula cu ajutorul ecuatiei 84:
W(G) = 4h3 + 16h2 + 6h + 1 (84)
3.2.1.7. Indicele Hyper-Wiener
Indicele Hyper-Wiener R a fost introdus in literature de specialitate pentru prima data in cazul structurilor aciclice de catre Randic [147]. Pentru un arbore T, indicele R, R =R(T) se poate defini cu ajutorul ecuatiei 85 [147, 148]:
![]()
in care prs reprezinta calea ce conecteaza varfurile r si s ale lui T iar rXprs si sXprs reprezinta numarul de varfuri de o parte si de alta a caii prs incluzand varfurile r si s.
In cazul unui graf conectat G cu N varfuri indicele R se poate defini cu ajutorul ecuatiei 86 [133, 148]:
![]()
Randic et all. pe de o parte [149] si Lukovits si Linert pe de alta parte [150] extind definitia originala a indicelui R (ecuatia 85) la structurile ciclice. Noua forma a indicelui R este prezentata cu ajutorul ecuatiei 87:
![]()
In aceasta ecuatie dij reprezinta distanta dintre varfurile i si j. Al doilea termen din ecuatia 87 reprezinta chiar indicele Wiener W(G) in timp ce primul termen este notat [133] cu D2 astfel incat aceasta ecuatie se poate scrie ca:
R = (D2 + W)/2 (88)
O alta forma a ecuatiei 88 este prezentata de Balaban in referinta [63]:

Dupa cum este cunoscut pentru structurile ciclice :W = N3/8 daca N este par si W = (N3 - N)/8 daca N este impar.
Cu aceste formule si luand in considerare si ecuatiile 87 si 88 se pot defini indicii Wiener in cazul structurilor ciclice cu ajutorul ecuatiilor 90 si 91:
Rciclu = (N4 + 3N3 - N2 - 3N) / 48 pentru N impar (90)
Rciclu = (N4 + 3N3+2N2) / 48 pentru N par (91)
3.2.1.8. Indici Wiener de ordin superior
Indicele Wiener clasic prezinta o degenerare intamplatoare (in cazul alcanilor superiori C7) iar indicii Wiener de ordin superior propusi de Randic [149] nu prezinta o abilitate buna de discriminare in cazul izomerilor. Avand in vedere aceste considerente Diudea et all. propun un nou algoritm de calcul [111, 119] al indicilor Wiener de ordin superior eWM.
eWM = (1/2)Σi eWM,I = (1/2)ΣiΣj[Me]ij (92)
Aceste tipuri de indici conduc la o buna corelare cu cifrele octanice ale mai multor alcani izomeri [119].
Aplicatii chimice ale indicelui Wiener clasic
Indicele Wiener clasic W(G) a fost utilizat in studiul coeficientului de partitie n-octanol/apa (indicator al caracteristicilor de transport si interactiune intre receptor si molecula bioactiva) [151]. In acest sens Alina Pyka utilizeaza un set de indici topologici pentru modelarea activitatii biologice si a valorilor RM in cazul unor fenoli [152] si clorofenoli izomeri [153], derivati de acid benzoic [154] sau alcooli [155] obtinand coeficienti de corelare mari atunci cand se utilizeaza indicele Wiener.
Se cunosc studii in care indicele Wiener este utilizat cu succes pentru prezicerea volumelor molare in cazul unor serii omologe de acizi cand se obtin coeficienti de corelare mai mari de 0.980 [156], pentru prezicerea presiunii de vapori in cazul a 476 substante chimice cand se obtin coeficienti de corelare mai mari de 0.900 sau a cifrei octanice conducand la coeficienti de corelare ce variaza intre 0.740-0.998 [158].
Un alt domeniu in care acest indice isi are o larga aplicabilitate este in modelari QSPR ale punctelor de fierbere [159], volumelor molare [156, 159], indicelui de refractie [159], caldurilor de izomerizare si vaporizare pentru diferite clase de compusi [62].
S.Basak si colaboratorii [160] utilizeaza indicele Wiener alaturi de alti indici topologici si geometrici in corelatii cu punctele de fierbere si coeficientul de partitie n-octanol/apa pentru 219 compusi chimici obtinand un coeficient de corelare r = 0.963 pentru modelul QSPR de determinare a punctului de fierbere si r = 0.912 in cazul modelarii coeficientul de partitie n-octanol/apa.
In literatura de specialitate mai recenta W(G) este utilizat la realizarea unui model QSAR eficient pentru prezicerea mutagenicitatii unor amine aromatice si heteroaromatice [161], a activitatii inhibitorii a unor benzamidine [162] sau in modelarea activitatii antituberculoase a unor derivati chinolonici[163].
Un alt domeniu unde W(G) se utilizeaza cu succes este gaz-cromatografia [164]. In acest sens timpii de retentie cromatografici (CRT) pentru monoalchil si O-dialchil benzeni sunt modelati cu W(G) [165] asa cum reiese din ecuatia 93 :
CRT=a Web g (93)
unde a b g sunt parametri determinati empiric.
Studii similare s-au efectuat pentru cumarine [166].
Un caz special de utilizare a indicelui Wiener clasic este in modelarea QSPR a energiei vibrationale [167].
Aplicabilitatea indicelui Wiener clasic pentru descrierea proprietatilor farmacologice ale compusilor este trecuta in revista in mai multe lucrari din literatura de specialitate (activitate fungicida pentru derivatii acidului salicilhidroxamic [168], activitate antivirala pentru analogi nucleosidici de 5-vinil-pirimidina [169], complecsi ai aminoacizilor cu Cu(II) [171, 172]).
Indici Wiener contrarii
Diametrul d al unui graf este distanta topologica cea mai mare intre doua varfuri, valoarea dij fiind cea mai mare intre toate distantele din matricea topologica. Prin scaderea din d a fiecarei valori dij se obtine o noua matrice simetrica care are valoarea 0 pe diagonala si perechea din afara diagonalei matricei cu valoarea 0 corespunde diametrului din matricea de distante.

unde [D]ij este elementul ij din matricea de distante D care este egal cu distanta din graf intre varfurile vi si vj. Sumele peste toate randurile i, sau coloanele i ale acestei matrici au fost notate cu i Insumarea tuturor i reprezinta chiar indicele Wiener invers [172] care se poate prezenta cu ajutorul ecuatiei 95
![]()
In Figurile 48-53 sunt prezentate matricile Wiener si matricile Wiener inverse iar in Tabelul 7 sunt prezentati indicii Wiener si Wiener inversi pentru : n-pentan (1), 2-metil-butan (2) si 2,2-dimetil-propan (3).


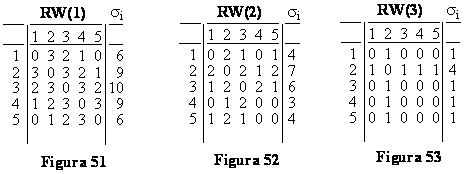
|
Compusul |
W(G) | |
|
n-pentan(1) | ||
|
2-metil-butan(2) | ||
|
2,2-dimetil-propan(3) |
Tabelul 7. Indicii Wiener si Wiener inversi pentru n-pentan (1), 2-metil-butan (2) si 2,2-dimetil-propan (3) [172]
O formula generala care leaga indicele Wiener si Wiener invers este prezentata in ecuatiile 96, 97:
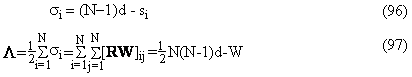
Indicele Wiener invers a fost utilizat cu succes in prezicerea punctului de fierbere, energia Gibbs standard de formare, entalpia de vaporizare, indicele de refractie si densitatea pentru 134 de alcani intre C6 si C10 cand se obtin coeficienti de corelare mai mari de 0.950 [172].
3.2.1.11. Indicii Quasi-Wiener si Kirchhoff
Matricea Laplace (Subcapitolul 2.6) reprezinta metrica de pornire in constructia indicelui Quasi-Wiener care este definit [104, 173] cu ajutorul ecuatiei 98:
![]()
unde λi (i = 1, 2, .., N) reprezinta valorile
proprii din matricea
Matricea distantelor-rezistenta (Subcapitolul 2.9) definita pentru prima data in literatura de specialitate de catre Klein si Randic [112] este utilizata pentru definirea unui descriptor topologic numit indicele Kirchhoff [174, 175]:
Kf = NTr(L*) (99)
unde Tr(L*) reprezinta inversa Moore-Penrose a matricei Laplace[176].
Cele doua tipuri de indici au fost utilizate cu bune rezultate in corelatii cu punctele de fierbere ale unor alcani [104].
3.2.2. Indicele Hosoya
Pentru un graf G, H. Hosoya propune [177] un alt descriptor molecular numit indicele Z a carui definitie este data prin ecuatia 100:
![]()
unde p(G,k) reprezinta numarul de moduri in care k muchii din graf pot sa fie alese astfel incat doua dintre acestea sa nu fie adiacente.
Pentru arbori exista o relatie simpla intre Z si valoarea absoluta a coeficientilor in polinomul caracteristic al grafului obtinut prin introducerea variabilei x pe diagonala principala a matricei de adiacenta A si egalarea determinantului obtinut cu 0. Suma acestor valori absolute ale coeficientilor polinomului caracteristic grafului G reprezinta tocmai valoarea indicelui Z [129, 177].
![]()
unde s este cel mai mare numar de muchii neconectate una cu alta iar E reprezinta matricea unitate.
Acest tip de indice a fost utilizat in corelatii cu punctele de topire, entropia sau ordinele de legatura calculate pentru mai multe clase de compusi chimici [177, 178].
3.2.3. Indicii Platt si Gordon-Scantlebury
Simultan cu indicele Wiener in literatura de specialitate apare un descriptor molecular definit de Platt [179] ca indicele F. Acesta reprezinta suma numarului de legaturi adiacente cu fiecare legatura din molecula. In teoria grafurilor aceasta definitie este echivalenta cu suma gradelor tuturor muchiilor [128, 129, 179].
Gordon si Scantlebury propun in anul 1964 un indice N2 [180] care reprezinta numarul de moduri distincte in care un fragment C-C-C se poate suprapune peste un schelet de atomi de carbon (graf fara hidrogen). S-a demonstrat faptul ca F = 2N2 [180] unde F este indicele Platt. In referinta [180] sunt discutate si alte formule caracteristice indicelui N2 care sunt prezentate in ecuatiile 102, 103:

3.2.4. Indicii Zagreb
Indicii Zagreb si variantele acestora au fost introdusi literatura de specialitate pentru studiul complexitatii moleculare [181, 182] si a chiralitatii [183]. Versiunea originala a acestor indici este definita cu ajutorul ecuatiilor 104 si 105 avand ca punct de plecare matricea de adiacenta A(G) [50, 184]:

unde d(i) reprezinta gradul varfului i iar d(i)d(j) este ponderea muchiei i-j.
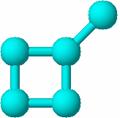
In Figura 54 este prezentat graful molecular 2-metilbutan (54a), matricea de adiacenta caracteristica (54b) si valorile indicilor Zagreb corespunzatoare (54c) [182].

![]()
54a 54b 54c
Figura 54. Graful molecular 2-metilbutan, matricea de adiacenta caracteristica si valorile indicilor Zagreb
3.2.4.1. Alte versiuni ale indicilor Zagreb
In ultimii ani in literatura de specialitate au aparut mai multe lucrari care trateaza alte versiuni ale indicilor Zagreb originali. S. Nikolic et all. utilizeaza in ecuatiile 104 si 105 valorile inverse pentru gradurile varfurilor obtinand o prima versiune a indicilor M1 si M2 numiti indicii Zagreb modificati m M1 respectiv m M2 a caror valoare analitica este prezentata cu ajutorul ecuatiilor 106 respectiv 107 [50, 186] :
mM1 = Σvarfuri1/[d(i)d(i)] = Σvarfuri[d(i)d(i)]-1 (106)
mM2 = Σmuchii1/[d(i)d(j)] = Σmuchii[d(i)d(j)]-1 (107)
In Figura 55 se prezinta contributia ponderilor la valorile indicilor m M1 si m M2 calculati pentru 2,4-dimetilpentan.

55a 55b 55c
Figura 55. Formula structurala (55a) si ponderea varfurilor (55b) respectiv a muchiilor (55c) la calculul valorile indicilor m M1 si m M2 in cazul 2,4-dimetilpentanului
Ecuatiile 104-107 pot fi scrise la modul general cu ajutorul ecuatiilor 108 respectiv 109:

Pentru =1, ecuatia 108 se reduce la ecuatia 104 iar ecuatia 109 la ecuatia 105 in timp ce pentru = -1 ecuatia 108 se reduce la ecuatia 106 iar ecuatia 109 la ecuatia 107.
Valorile acestor versiuni ale indicilor Zagreb au fost utilizate in corelari cu punctele de fierbere ale alcanilor C3-C8 cand se obtin coeficienti de corelare mai mari ca 0.950 [185, 186].
3.2.4.2. Calculul indicilor Zagreb pentru hidrocarburi benzenoide
Conceptul din chimia hidrocarburilor benzenoide conform caruia atomii de carbon adiacenti cu alti doi atomi de carbon au caracteristici diferite de acei atomi care sunt adiacenti cu alti trei atomi de carbon [187] poate fi explicat cu ajutorul teoriei grafurilor prin utilizarea notiunii de grad al varfului. Se poate scrie asadar pentru un atom de carbon adiacent cu alti doi atomi ecuatia 110:
d = 2 + x (110)
iar pentru un atom de carbon adiacent cu alti trei atomi de carbon, ecuatia 111:
d = 3 + y (111)
Tinand cont de ecuatia 106, 110 si respectiv 111 se poate scrie forma generala pentru indicele Zagreb vM2i in cazul unei hidrocarburi benzenoide i [188]:
vM2i = c1i(2+x)2 + c2i(2+x)(3+y) + c3i(3+y)2 (112)
Indicele Zagreb vM2i a fost utilizat cu succes in corelari cu punctele de fierbere la presiune normala ale hidrocarburilor benzenoide prezentate in Figura 56 [188].



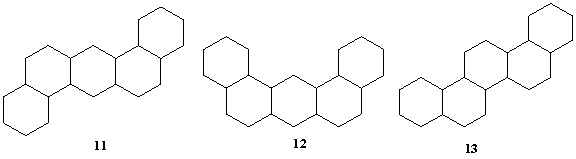


Figura 56. Grafurile moleculare pentru hidrocarburile benzenoide luate in studiu
In Tabelul 8 sunt
prezentate punctele de fierbere si parametrii c1i, c2i si c3i utilizati in calculul valorilor
indicele
|
Hidrocarbura benzenoida |
bpi |
c1i |
c2i |
c3i |
Tabelul 8. Punctele de fierbere si parametrii c1i, c2i si c3i utilizati in calculul valorilor
indicele
I. Gutman si N. Trinajstic descopera [184] o relatie intre primul
indice
F = 2N2=M1-e (113)
Un alt domeniu important in care indicii Zagreb clasici sau versiunile acestora isi gasesc aplicabilitate este acela de modelare QSAR a activitatii anti-inflamatorii pentru 112 acizi N-arilantranilici [189].
3.2.5. Indici centrici
Alte tipuri de indici care nu depinde de invariantii locali ai grafurilor calculati din matricile de adiacenta A sau de distante D dar care exprima modul in care varfurile grafului sunt grupate in jurul centrului grafului sau centroidului grafului au fost propusi de Balaban in anul 1979 [190].
Pentru a gasi centrul sau bicentrul unui arbore, varfurile si muchiile incidente sunt sterse unul cate unul, operatia repetandu-se pana la obtinerea centrului(bicentrului). Operatia se numeste scurtarea grafului [128, 129, 190] iar numarul de puncte sterse in primul, al doilea,.., ultimul stadiu de scurtare se noteaza cu r. Numarul r se numeste raza arborelui [191] sau excentricitatea minima.
In Figura 57 este prezentat modul de obtinere a centrului (57a) respectiv a bicentrului (57b) in cazul a doi izomeri ai C7H16 ambii izomeri avand 7 varfuri si r =3 [128, 190]. Cu "o" sau notat varfurile conectate prin muchii (linii punctate) care in pasul urmator vor fi sterse iar cu "●" sa notat centrul respectiv bicentrul celor doi izomeri ai heptanului.

57a 57b
Figura 57. Modul de obtinere a centrului (57a) respectiv a bicentrului (57b) in cazul a doi izomeri ai C7H16 ambii izomeri avand 7 varfuri si r =3.
Secventa numerelor r se noteaza cu S si reprezinta punctul de pornire in definirea [128, 190] indicelui centric B :
![]()
Pentru graful prezentat in Figura 57a valoarea indicelui B = 21 iar pentru cel prezentat in Figura 57b B = 17.
3.2.5.1. Indicii centrici normalizati si binormalizati (C, C') si indicii quadratici
(Q, Q')
S-a demonstrat faptul ca numarul de moduri in care un fragment C-C*-C se poate suprapune peste un arbore ce contine atomi de carbon astfel incat gradul varfului reprezentat de atomul central C* sa coincida cu gradul varfului vi este (vi 2) - lipseste operatorul (exemplu 6 pentru vi = 4 si 3 pentru vi = 3). Avand in vedere aceste considerente primul indice Zagreb M1 si indicele Gordon-Scantlebury N2 se pot defini cu ajutorul ecuatiilor 115 respectiv 116:
M1 = 16V4 + 9V3 + 4V2 + V1 (115)
N2 = 6V4 + 3V3 + V2 (116)
unde Vv reprezinta numarul de varfuri de gradul v.
Cele doua tipuri de indici M1
respectiv N2 apartin
aceleasi clase de indici topologici a caror expresie generala este ![]() Vv f(v) in care f(v) este polinomul quadaratic in v. Aceasta clasa de indici topologici formeaza clasa indicilor quadratici. Pentru M1, f(v) = v2 iar
pentru N2 f(v) = (v2-v)/2.
Vv f(v) in care f(v) este polinomul quadaratic in v. Aceasta clasa de indici topologici formeaza clasa indicilor quadratici. Pentru M1, f(v) = v2 iar
pentru N2 f(v) = (v2-v)/2.
Pentru a reflecta forma topologica a grafurilor aciclice exprimate ca doua extreme se defineste [190] un indice quadratic normalizat Q cu ajutorul ecuatiei 117:
Q i(i2-2i)Vi +2] / 2 (117)
unde Vi este numarul de varfuri cu gradul i din graf.
Pentru arbori continand atomi de carbon prin comparatie cu ecuatiile 115 si 116, indicele quadratic normalizat se poate reprezenta cu ajutorul ecuatiei 118:
Q = (8V4 + 3V3 - V1 + 2) / 2 (118)
Pentru un arbore cu n varfuri ce contine atomi de carbon sunt valabile urmatoarele relatii:
V1 = 2 + V3 + 2V4 si V2 = n - 2 - 2V3 - 3V4 (119)
Cu ajutorul ecuatiilor 119, indicele Q se poate defini astfel:
Q = 4V4 + 3/2V3 + 1 - 1/2V1 = 3V4 + V3 (120)
Intre indicii Q, M1 si N2 exista de asemenea relatiile:
Q = N2 - n + 2 = 3 - 2n + M1/2 (121)
M1 = 2(N2 + n - 1) (122)
In aceasi mod ca indicele Q se poate defini si un indice centric normalizat C cu ajutorul ecuatiei 123 [190]:
C = [ j(j2 - 2j)zj + U] / 2 = (B - 2n + U) / 2 (123)
unde U = [1-(-1)n]/2 iar B este indicele centric definit in ecuatia 114.
Pentru un graf-stea (graf bipartit complet format dintr-un varf central adiacent cu alte n varfuri neadiacente intre ele) se pot defini alte doua grupe de indici: indicele quadratic binormalizat (ecuatia 124) si indicele centric binormalizat (ecuatia 125):


Indicele centric binormalizat C' este limitat doar la arbori in timp ce indicele quadratic binormalizat poate fi calculat pentru orice graf.
Pentru un graf ciclic(inel cu n varfuri) este valabila relatia :Q' = 8n/ (n-2)(n-3) in timp ce pentru un graf cubic in care toate varfurile au gradul 3 ( exemplu izomerii de valenta ai anulenelor [192]) Q' se poate calcula cu relatia : Q' = 18n/ (n-2)(n-3).
O partitie grafica P a gradelor varfurilor poate fi prezentata sub forma: P = v1, v2,.,vn.
In Tabelul 9 sunt prezentati comparativ indicii B, M1, C si Q pentru grafurile-stea si arborii cel mai putin ramificati (grafuri-lant) cu n varfuri. U se calculeaza cu relatia U = [1-(-1)n]/2.
|
Partitia si indicele |
Grafurile-stea |
Grafuri-lant |
|
Partitia grafica P |
n-1, 1n-1 |
2n-2, 12 |
|
Indicele M1 |
n2-n |
4n-6 |
|
Indicele Q |
(n-2)(n-3) / 2 | |
|
Partitia S |
1, n-1 |
U, 2(n-U) / 2 |
|
Indicele B |
(n-1)2 + 1 |
2n-U |
|
Indicele C |
[(n-2)2 - 2 +U] / 2 |
Tabelul 9. Prezentarea comparativa a indicilor B, M1, C si Q pentru grafurile-stea si arborii cel mai putin ramificati (grafuri-lant) cu n varfuri
Indicii prezentati in Subcapitorul 3.2.5. au fost utilizati in corelatii liniare cu cifrele octanice pentru heptanii izomeri [193].
3.2.6. Indicele Harary
Pentru determinarea indicelui Harary se porneste de la reciproca unei matrici M care se defineste [RM]ij=1/[M]ij daca [M]ij este diferita de zero si [RM]ij=0 daca [M]ij=0. Indicele Harary este definit conform ecuatiei 126 [79, 80, 108,194-198].
HM i j [RM]ij (126)
Indicele Harary original, HDe, se construieste din matricea reciproca de distante, RDe [79, 80]. Pentru indicele Wiener nu se observa nici o degenerare in timp ce pentru indicele Harary degenerarea depinde de gradul de ramificare al moleculei. Acest indice a fost testat [108, 195] in corelatii cu punctele de firbere si razele van der Waals ale octanilor. Prin analogie cu HDe, Diudea [108] propune indicele HWe care deriva din matricea Wiener reciproca. Acest indice se coreleaza cu cifra octanica atat in regresie liniara (r = 0.971) cat si parabolica (r = 0.991).
In Tabelul 10 se prezinta indicele Wiener, We si indicii de tip Harary, HDe, HWe pentru octani.
|
Compusul |
We |
HDe |
HWe |
|
n-octan | |||
|
3-etil-hexan | |||
|
3-etil-3-metil-pentan | |||
|
2,2,3,3-tetrametil- butan |
Tabelul 10. Indicele Wiener, We si indicii de tip Harary, HDe, HWe pentru octani
3.2.7. Indici de tip Schultz
Trinajstic si colaboratorii [199] si de asemenea Gutman [200] descriu indicele MTI'care deriva din matricea D si vectorul valentelor (v) pentru un graf cu N varfuri. Schultz si colaboratorii inlocuiesc MTI'prin S care poate fi definit cu ajutorul ecuatiei 127 [201] :
![]()
Geometria perechii de varfuri responsabile pentru izomeria geometrica generata de dubla legatura atat in cazul sistemelor ciclice cat si aciclice poate fi indicata prin factorul geometric GF care este +1 si +1 pentru izomerul Z (cis) respectiv -1 si -1 pentru izomerul E (trans). Toate celelalte varfuri au valoarea 0 pentru GF. Acest factor geometric GF a fost inclus in indicele descris de ec. (127) pentru a cuantifica si izomerii geometrici ai diversilor compusi [50, 129, 201].
In lucrarile ulterioare Schultz propune si alti indici care deriva din cel calculat prin ec. (127) cum ar fi : permanentii si produsul sumelor pe randuri [202] precum si a hafnianului [203]. Din factorul geometric GF se obtine conform strategiei de mai jos factorul de izomerism modificat GM.
![]()
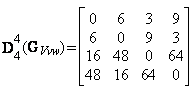
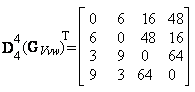
Figura 58 Matricile Vv, transpusa (Vv) si graful molecular pentru 1,2-difluoroetan

Suma matricilor D si DT este intotdeauna o matrice simetrica [204].


Figura 59 Matricile diagonale corespunzatoare celor doi stereocentri pentru Z (cis) si E (trans)

Valoarea GM rezultata din sumarea tuturor randurilor matricii de mai sus este pentru (Z)-1,2-difluoroetan este +176 iar pentru (E)-1,2-difluoroetan este -176. Luand in considerare aceste valori pentru GM se obtine pentru indicele S valoarea 1308 in cazul (Z)-1,2-difluoroetanului si 956 in cazul (E)-1,2-difluoroetanului.
Acesti indici au fost utilizati in corelari cu refractia molara RM pentru diastereoizomerii Z si E obtinandu-se rezultate foarte bune.
|
Compusul |
Izomerul |
RMa,b |
indicele DNN(GVvw) |
||||
|
S |
PRS |
det |
per |
1haf |
|||
|
2-pentena |
(Z)- | ||||||
|
(E)- | |||||||
|
2-hexena |
(Z)- | ||||||
|
(E)- | |||||||
|
3-hexena |
(Z)- | ||||||
|
(E)- | |||||||
|
2-heptena |
(Z)- | ||||||
|
(E)- | |||||||
aRM = refractia molara = (n2-1/n2+2)(M/d) [205]; Calculat din nD20 si d420
Tabelul 11. Descriptorii derivati din matricea de distante pentru izomerii geometrici ai unor alchene
Tehnica generala de obtinere a indicilor topologici pentru izomerii geometrici a fost extinsa si la izomerii optici. Configuratiei R a stereocentrului grafului i s-a atribuit factorul chiral (CF) +1 iar configuratiei S valoarea -1.
3.2.7.1. Teoria grafurilor si indicii topologici moleculari Schultz pentru cicloalcani
Scultz si colaboratorii [206] au extins modelel lor si la cicloalcani. In Tabelul 12 este prezentata influenta valentei, adiacentei si distantei pentru seturi de varfuri in cazul alcanilor si cicloalcanilor aratandu-se diferentele de complexitate pentru toate varfurile secundare in cazul perechilor : propan-ciclopropan, butan-ciclobutan.
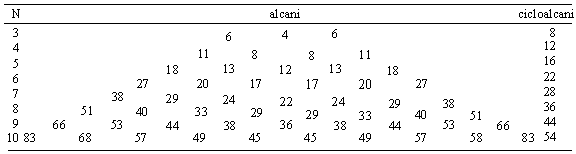
Tabelul 12 [206]. Complexitatea varfurilor pentru alcani si cicloalcani C3-C10
Au fost calculati indicii conform teoriei lui Schultz [206] pentru alcani si cicloalcani C3-C10 iar valorile acestora au fost corelate cu punctele de fierbere. In cazul alcanilor se obtin coeficienti de corelare cuprinsi intre 0.956-0.998 iar in cazul cicloalcanilor coeficientii r sunt mai mari de 0.990.
In Tabelul 13 sunt prezentate valorile indicilor calculati pentru cicloalcani C3-C10.
|
Compus |
Punct de fierbere,˚C (cis/trans) |
v·D |
V(A+D) |
det|D| |
Per (D) |
PRS (D) |
Shaf (D) |
1haf (D) |
|
ciclopropan | ||||||||
|
ciclobutan | ||||||||
|
Etilciclo propan | ||||||||
|
1-etil-3-metilciclobutan | ||||||||
|
1-ciclopropilbutan | ||||||||
|
ciclohexan | ||||||||
|
cicloheptan | ||||||||
|
ciclooctan | ||||||||
|
ciclononan | ||||||||
|
ciclodecan |
Tabelul 13. Valorile indicilor Schultz pentru cicloalcani C3-C10 [206]
I. Gutman arata in referinta [207] ca indicele Schultz se poate rescrie cu ajutorul ecuatiei 128 :
![]()
unde A este matricea de adiacenta iar D este matricea de distante.
Klein et all. obtin pentru grafurile aciclice o relatie remarcabila intre MTI si W(indicele Wiener) [208]:
MTI = 4W + 2P2 - (N-1)(N-2) (129)
unde P2 este numarul de cai de lungime 2:
![]()
si deoarece graful aciclic are N varfuri si N-1 muchii prin combinarea ecuatiilor 127, 128 si 129 se obtine [207]:
S = 4W -N(N-1) (131)
3.2.8. Indicele Pogliani
Pornind de la indicele Randic, Pogliani construieste un nou indice geometric [209].
![]()
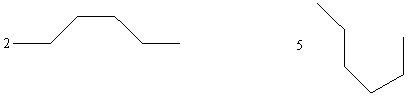

Figura 60 Cei sase comformeri ai hexatrienei
Daca se suprapun izomerii conformationali ai hexatrenei (Figura 60) peste o suprafata de grafit ideala dupa care se scade valenta δ cu o unitate pentru doua puncte cis urmata de conectarea acestor puncte print-o muchie, grafurile chimice 2-6 pot forma inele de patru membrii, un inel cu cinci membrii (grafurile 2 si 3), doua inele cu cinci membrii (grafurile 4 si 5) si trei inele cu cinci membrii (graful 6). Pogliani defineste in acest fel un indice de conectivitate cis (ecuatia 132) :
nXc = S d rd dnr)-6/n (132)
unde c este abrevierea de la cis iar 6 si n de la exponent reprezinta numarul muchiilor inelelor virtuale formate.
Deoarece indicele prezentat cu ajutorul ecuatiei 132 nu se aplica si structurilor trans a fost definit un indice global de conectivitate moleculara (ecuatia 133):
Xct = 1X- nXc (133)
X este MCI de ordinul unu iar nXc are valori diferite de 0 doar pentru inele virtuale in conformatie cis.
In cazul structurilor trans nXc = 0 astfel incat indicele global de conectivitate moleculara devine:
Xct = 1X = S didj)-1/2 (134)
unde i si j reprezinta atomii adiacenti iar limitele sumarii sunt toate perechile de atomi adiacenti.
Pogliani propune totodata pentru hidrocarburile nesaturate si un indice care sa tina cont si pozitia dublei legaturi.
Xct(p) = Xct-(1/p)n (135)
|
Olefina |
X |
Xct |
bp |
nD20 |
d420 |
MRD |
|
trans-3-hexena | ||||||
|
cis-3-hexena | ||||||
|
trans-3-octena | ||||||
|
cis-3-octena | ||||||
|
trans-4-octena | ||||||
|
cis-4-octena |
Tabelul 14. 1X, Xct si constantele fizice pentru olefine cis/trans [210]
Indicele Pogliani se utilizeaza cu succes in corelari cu punctul de fierbere , bp [209], indicele de refractie, nD20 [209], densitatea, d420 si refractia molara, MRD [209].
3.2.9. Indicele Estrada
In contextul teoriei grafurilor chimice, molecula este considerata un graf simplu
G = , unde V =este setul de varfuri reprezentand atomii si E = este setul de muchii reprezentand legaturile moleculei. Avand in vedere aceste considerente, Estrada propune un indice nou pentru corelari cu densitatea electronica de sarcina [211]. Densitatea electronica de sarcina a atomului i (qi) se poate calcula prin metode cuantice utilizand expresia :
qi =Zi -Sm(PS)mm (136)
in care Zi este sarcina nucleara, P este matricea densitatii, S este matricea de intrepatrundere iar Sm(PS)mm este populatia Mulliken [212].
Densitatea de sarcina de conectivitate d(qi)se poate calcula cu ajutorul formulei de mai jos in care qi se calculeaza utilizand ec.
di(q) = qi - hi (137)
Pe baza ec.(136), (137) Estrada propune indicele [211]:
W(q) = Sk di(q) dj(q)]k-1/2 (138)
Pentru a se tine cont si de densitatea electronica a hidrogenului se poate calcula densitatea electronica corectata a fiecarui atom conform ec. (139) :
dC(qi) = qi- j qhj (139)
qhj este densitatea electronica de sarcina a celor hj atomi de hidrogen pentru atomul i.
Calcularea indicilor W se face utilizand densitatea electronica de sarcina calculata prin metoda semiempirica AM1 [213].
a)

b) Calculul densitatii de sarcina de conectivitate pentru fiecare atom din propena
d (q) = 4.1699-2 = 2.1699 d C(q) = 4.1699-1.8398 = 2.3301
d (q) = 4.1360-1 = 3.1360 d C(q) = 4.1360-0.9063 = 3.2297
d (q) = 4.0781-3 = 1.0781 d C(q) = 4.0781-2.8697 = 1.2084
c) Calculul indicilor W
W(q) = 0.9272
WC(q) = 0.8708
Figura 61 Calculul indicilor W pentru propena : (a) valoarea densitatii electronice pentru fiecare atom al moleculei (I) si graful molecular pentru propena(II) ; (b) calcularea densitatii de sarcina de conectivitate pentru fiecare atom din molecula de propena ; (c) calculul indicilor W
Indicele molar de conectvitate si descriptorii tridimensionali W(q) si WC(q) sunt utilizati in QSPR pentru prezicerea punctelor de fierbere a 53 de alchene C4-C8.
|
Alchena |
pf(0C)(exp.) |
pf(0C)(calc.) |
W(q) |
WC(q) |
|
cis-2-butena | ||||
|
2-Me-2-butena | ||||
|
1-hexena | ||||
|
4,4-diMe-1-pentena | ||||
|
trans-2-octena |
Tabelul 15. Valorile punctelor de fierbere experimentale si calculate(in 0C) utilizand indicii topologici W(q) WC(q) pentru o serie de alchene.
3.2.10. Indicii Alina Pyka
Pentru investigarea indicilor topologici si relatiilor dintre acestia si valoarea RM a izomerilor separati prin TLC (Thyn Layer Chromatography), Alina Pyka propune un indice topologic [66] care s-a utilizat cu bune rezultate in corelarile cu RF si RM.
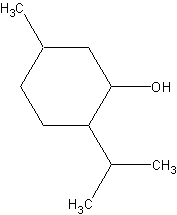
Figura 62. Formula generala si graful molecular fara hidrogeni pentru mentol

Figura 63. Matricea de distante pentru mentol, neomentol, izomentol si neoizomentol
Daca gruparea hidroxil este in pozitie ecuatoriala atunci valoarea varfului reprezentat de atomul de oxigen este negativa (de exemplu -5) iar daca este in pozitie axiala atunci valoarea varfului reprezentat de atomul de oxigen este pozitiva (de exemplu +5). Daca gruparea metil si gruparea hidroxil au configuratie cis atunci valoarea varfului reprezentat de atomul de carbon este pozitiva (de exemplu +1) iar daca au configuratie trans valoarea este negativa (de exemplu -1).
Din matricea de distante (D) se construiesc vectorii coloana v(vmentol, vneomentol, vizomentol, vneoizomentol).
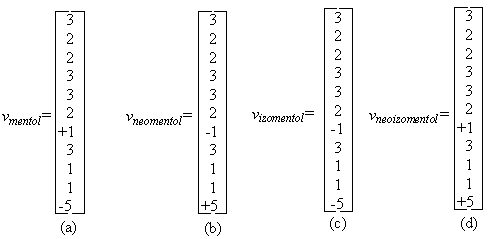
Figura 64. Vectorii coloana v pentru : (a)-mentol ; (b)-neomentol ; (c)-izomentol;
(d)-neoizomentol
Urmatorul pas in construirea indicelui ISTI este realizarea produsului dintre matricea de distante [D] si vectorul coloana v obtinandu-se vectorul coloana SSTI(i).
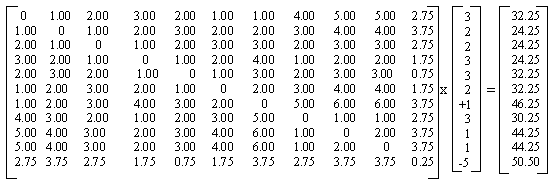
[D] vmentol Smentol
Indicele topologic stereoizomeric (ISTI) se calculeaza conform ec.(34)
![]()
ISTI
In mod analog se calculeaza indicii ISTI si pentru izomentol, neomentol si izoneomentol.
Alina Pyka propune o tehnica analoga si pentru construirea unui indice in cazul izomerilor optici [54].
ISTI a fost aplicat in corelatii cu RM pentru prezicerea activitatii biologice in cazul unor fenoli si clorofenoli izomeri [153] sau in cazul unor alcooli izomeri [214] obtinandu-se coeficienti de corelare buni.
Rezultate bune cu ISTI se obtin si in cazul unor separari cromatografice ale unor izomerilor ai alcooli [155, 214] sau in cazul unor acizi [215].
3.2.11. Indicele Detour
Indicele Detour ω se defineste in aceasi mod ca si indicele Wiener W(G) fiind egal cu semisuma elementelor matricei Detour D
![]()
In cazul structurilor aciclice indicele ω (in alte lucrari se utilizeaza notatia w(G)) este echivalent cu indicele Wiener W(G) in timp ce pentru structurile ciclice w(G) este diferit de W(G) [216].
Pentru un graf complet KN cu N varfuri si M muchii este valabila relatia 142 [87] :
= M(N-1) = Md (142)
unde d = N-1.
P. E. John arata [217] ca intre indicele Detour si indicele Wiener W(G) exista o relatie de forma :
= (N-1)W (143)
In cazul structurilor ciclice, acest tip de indice se poate calcula cu ajutorul ecuatiei 144 :
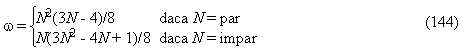
sau utilizand indicele Wiener ecuatia 144 se poate scrie sub forma [87, 217, 218]:

Studiile privind matricea si indicele Detour au aratat [86, 219] ca exista grafuri care au aceeasi valoare a indicelui Detour dar matrici Detour diferite (Figura 65) dar si grafuri care au aceasi valoare a indicelui Detour deoarece matricile Detour sunt identice (Figura 66).
In Figura 65 sunt prezentate doua exemple de grafuri (65a-1metilciclobutan, 65c-spiropentan) care au aceasi valoare a indicelui Detour dar matricile Detour (65b si 65d) sunt diferite [89].
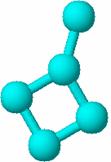

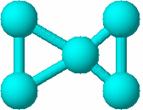
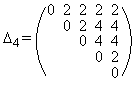
65a 65b 65c 65d
Figura 65. Grafuri (65a-1-metilciclobutan, 65c-spiropentan) care au aceasi valoare a indicelui Detour dar matricile Detour (65b si 65d) diferite [89]
1-metilciclobutan : (G) = 13 + 12 + 3 = 28
spiropentan : (G) = 12 + 16 = 28
In Figura 66 sunt prezentate doua exemple de grafuri care au acelasi indice si matrice Detour [89].
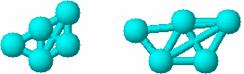
Figura 66. Tipuri de grafuri care au acelasi indice si matrice Detour [89]
Lukovits utilizeaza cu succes indicele Detour [219] pentru explicarea variatiei punctelor de fierbere in cazul a 77 de alcani si cicloalcani (r = 0.977). Continuand cercetarile lui Lukovits, Trinajstic si colaboratorii [87] utilizeaza matricea Detour si implicit indicele corespunzator pentru modelarea punctelor de fierbere a 76 de alcani si cicloalcani obtinand un coeficient de corelare superior (r = 0.995). Un coeficient de corelare superior se obtine si atunci cand indicele (G) este utilizat in modelarea punctelor de fierbere in cazul a 32 de octani izomeri [88].
3.2.12. Indicii Szeged
Un analog al indicelui Wiener este indicele Szeged, SZ, care a fost propus recent de Gutman si colaboratorii [220, 221]. SZ se defineste prin analogie cu cu ec. (64) dar seturile Ni si Nj sunt definite atat pentru grafuri ciclice cat si aciclice.
We=We(G)= eNi,eNj,e (146)
Ni (147)
Nj (148)
Ni si Nj reprezinta cardinalii (numarul total de varfuri conectate prin muchii de varfurile i respectiv j) setului de varfuri care se termina in i respectiv j. Varfurile echidistante (la aceeasi distanta) i respectiv j fata de un varf luat drept reper nu sunt calculate. Luandu-se in considerare produsul NiNj se pot defini doua matrici simetrice Szeged SZe si SZp. In SZe intrarile (ij) sunt egale cu NiNj daca i si j sunt adiacente si 0 in celalalte cazuri. In SZp toate elementele matricii sunt egale cu NiNj. Se poate concluziona ca SZe reprezinta produsul dintre SZp si matricea de adiacenta A. In acelasi mod cu matrici simetrice Szeged SZe si SZp se poate defini si o matrice Szeged nesimetrica [115, 223] SZu. In SZu intrarile (ij) sunt egale cu Ni.
In Figura 67 sunt prezentate Matricile De, SZu si indicii corespunzatori pentru 2-metil-ciclohexan.
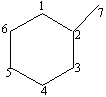
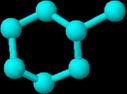
2-metil-ciclohexan


We = (1/2) i j[De]ij = 42 SZe = e[SZu]ij[SZu]ji = 78
SZp = p[SZu]ij[SZu]ji =182
Figura 67 Matricile De, SZu si indicii corespunzatori pentru 2-metil-ciclohexan
Indicii Szeged au fost testati cu bune rezultate [221], datorita abilitatii lor de discriminare a izomerilor. In acest sens indicii Szeged au fost utilizati impreuna cu alte categorii de indici in modelari ale punctelor de fierbere pentru o serie de cicloalcani [222] cand se obtin coeficienti de corelare mai mari de 0.950. Entalpia de formare a cicloalcanilor nesubstituiti de asemenea a fost descrisa cu ajutorul indicilor Szeged in corelari cu o singura variabila (SZe, r = 0.9813 ; SZp, r = 0.9623) sau cu doua variabile (SZe& We, r = 0.9912 ; SZp& We , r = 0.9910) [221].
3.2.13. Indicii Cluj
Matricile Cluj definite in Subcapitolul 2 [50,108-111] reprezinta sursa principala in calcularea indicilor Cluj CJe si CJp. Intre indicii Cluj, Szeged si indicele Wiener exista urmatoarele relatii: CJe(T) = SZe(T) = We(T) = De(T), CJe(T) = SZe(T) = We(T) ≠ De(T), CJp(T) = Wp(T) = De(T) ≠SZp(T), CJe(T) ≠ SZe(T) ≠ De(T) [109].
Indicii Cluj sunt utilizati cu succes in corelatii cu punctele de fierbere a 45 de cicloalcani(r = 0.920) [109]. Indicele de corelare creste daca pentru acest descriptor topologic se utilizeaza scara logaritmica (r = 0.991).
In Tabelul 16 sunt prezentate comparativ valorile pentru indicii Wiener, We, Szeged, SZe, SZp si Cluj, CJe, CJp pentru cicloalcani simpli.
|
Compusul |
We |
SZe |
SZp |
CJe |
CJp |
|
Ciclopropan | |||||
|
Ciclohexan | |||||
|
Ciclooctan |
| ||||
|
Ciclononan | |||||
|
Ciclodecan |
Tabelul 16. Indicii Wiener, We,
Prin analogie cu indicele hiper-Wiener se poate defini un indice hiper-Cluj CJp cu ajutorul ecuatiei 149 [109]:
CJp = CJe + CJΔ (149)
in care CJΔ = Σ(i,j)[CJu]ij[CJu]ji; |(i,j)|>1.
Pentru grafurile ciclice cu N varfuri CJe = SZe si sunt valabile urmatoarele relatii:
CJe = N(N-1)2 / 4 daca N = impar (150)
CJe = N 3 / 4 daca N = par (151)

Daca N = 2k + z si (N-z)/2mod2 = r atunci ecuatia 152 se poate scrie sub forma:
CJ = 7/6k4 +(7/3z + 1/2r - 11/4)k3 + (z2 - 2z + 1/4zr -2/3)k2 + (1/2zr - 5/6z + 1/2r - 3/4)k + 1/4zr - 1/2z (153)
In Figura 68 este prezentat graful ciclic (68a) impreuna cu matricea Cluj caracteristica (68b) si valorile indicelui hiper-Cluj (68c) [109].
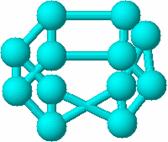

![]()
68a 68b 68c
Figura 68. Graful ciclic (68a) impreuna cu matricea Cluj caracteristica (68b) si valorile indicelui hiper-Cluj (68c) [109]
3.3. A doua generatie de indici topologici
Indicii topologici (TI) din a doua generatie sunt numere reale in timp ce invariantii locali ai varfurilor (LOVI) grafurilor, din care se pot construi astfel de indici topologici, sunt numere intregi.
3.3.1. Indicele topologic de tip Randic
In anul 1975 in literatura topologica, Randic introduce [224] un indice de conectivitate χR, prin similaritate cu M2, pentru a caracteriza gradul de ramificare moleculara
χR = (vivj)-1/2 (154)
iar daca se considera gradul de substitutie al tuturor nodurilor de-a lungul unui drum de lungime h, din graful molecular G si se extinde relatia din ec.(154) peste toate drumurile posibile de lungime h se obtine indicele de conectivitate generalizat [225, 226, 227].
hχR = (vivj....vh+1)-1/2 (155)
Deoarece indicele Randic in forma sa initiala nu face diferentierea intre atomii de carbon si heteroatomi, pentru a exista aceasta diferentiere dar si pentru includerea legaturilor multiple s-a propus o scara generalizata de indici hχRv in care valentele vi din ec.(155) sunt inlocuite prin conectivitatea atomica Div definita ca diferenta dintre numarul de electroni de valenta Ziv si numarul de atomi de hidrogen Hi legati de atomul i.
hχv = toate muchiile(ΔivΔjv....Δh+1v)-1/2 (156)
Div = (Ziv-Hi) / (Zi- Ziv-1) (157)
in care Ziv reprezinta numarul electronilor de valenta din atomul i care are numarul atomic Zi iar Hi reprezinta numarul atomilor de hidrogen legati de atomul i.
Modelarile punctelor de fierbere pentru o serie de alcani sau eteri utilizandu-se hχR conduc la coeficienti de corelare ceva mai mari fata de situatia cand heteroatomii sunt asimilati cu atomi de carbon [226]. Pentru diferentierea heteroatomilor si pentru a obtine valori diferite ale indicelui topologic pentru molecule descrise prin acelasi graf G, dar care se deosebesc prin natura chimica a atomilor componenti sau prin multiplicitatea legaturilor, se pot utiliza conectivitati van der Waals VAiw = Aivi (Ai = ri = Si = Vi, unde ri, Si, Vi reprezinta raza van der Waals, suprafata sau volumul vdW al atomului i in cadrul ec. (155).
In Tabelul 17 sunt prezentati comparativ indicele Randic, indicii de conectivitate van der Waals.
|
Alcani |
XR |
Xrw |
Xsw |
Xvw |
|
Propan | ||||
|
2-Me-Butan | ||||
|
2,2-diMe-Butan | ||||
|
2-Me-Pentan | ||||
|
Hexan |
Tabelul 17. Indicii de conectivitate van der Waals, comparativ cu indicele Randic
Razele utilizate in aceste calcule au fost determinate de Bondi [228], valoarea pentru carbon fiind 1.7 Å.
Indicii Xrw, Xsw, Xvw au fost utilizati cu rezultate bune pentru corelarea caracteristicilor gaz-cromatografice (timpi de retentie exprimati ca indici Kovats) ale alcanilor, alcoolilor, aldehidelor si esterilor [229, 230].
3.3.1.1. Indicele de conectivitate variabil
Indicele de conectivitate variabil f a fost introdus [231] si utilizat [232-235] ca o alternativa la indicii de conectivitate de valenta introdusi de Kier si Hall [225, 226, 227] pentru caracterizarea heteroatomilor in studii QSPR.
Acest tip de indice se poate construi din matricea de adiacenta modificata [231] iar elementele cu valoarea 0 de pe diagonala se inlocuiesc cu variabilele x, y, z,.... Fiecare dintre aceste variabile caracterizand diferite grupuri de atomi din molecula si modifica contributia legaturilor individuale. Modul de calcul pentru f este asemenator cu cel pentru indicele
f toate muchiile [(vi + x)(vj + x)]-1/2 (158)
In Tabelul 18 este prezentata matricea de adiacenta, matricea de adiacenta modificata, suma coloanelor, indicele de conectivitate 1 si indicele de conectivitate variabil 1 f pentru graful molecular caracteristic 3-metil-2-butanolului (Figura 69) [233].
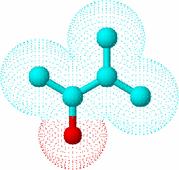
Figura 69. Graful molecular caracteristic 3-metil-2-butanolului
|
Suma coloanelor |
|||||||
|
= 4/√3 + 1/3 = 2.642734 |
|||||||
|
f = 3/√(1+x)(3+x) + 1/(3+x) + 1/√(3+x)(1+y) = f(x, y) |
|||||||
|
x |
1 + x |
||||||
|
x |
3 + x |
||||||
|
x |
3 + x |
||||||
|
x |
1 + x |
||||||
|
x |
1 + x |
||||||
|
y |
1 + y |
||||||
Tabelul 18. Matricea de adiacenta, matricea de adiacenta modificata, suma coloanelor, indicele de conectivitate 1 si indicele de conectivitate variabil 1 f pentru graful molecular caracteristic 3-metil-2-butanolului (Figura 69) [233]
Kier si colaboratorii, in urma studiilor intreprinse privind indicele de conectivitate [48, 225], arata ca trebuie facuta o diferentiere intre legaturile din structurile aciclice si cele din structurile ciclice. Pentru aceasta se propune o asa numita ,,corectie de inel'' adica din valoarea calculata a indicelui de conectivitate in cazul moleculelor ciclice se scade valoarea 1/2 pentru fiecare inel prezent in respectiva molecula.
Randic arata [234] ca trebuie facuta o diferentiere si in rolul jucat de atomii de carbon din structurile ce cuprind o parte aciclica si una ciclica. In acest fel se propune [234] un parametru a pentru atomii din partea aciclica si un parametru c pentru atomii din partea ciclica. Se pot scrie astfel trei tipuri de legaturi utilizand cei doi parametrii: Cc-Cc, Cc-Ca si Ca-Ca care corespund urmatoarelor ponderi: [(vi + c)( vj + c)]-1/2, [(vi +c)(vj +a)]-1/2
[(vi + a)( vj + a)]-1/2.
Pentru o mai usoara intelegere a modului de constructie a 1 f in cazul structurilor ce contin atat o parte ciclica cat si una aciclica, in Figura 70 este prezentat modul de constructie al 1 f si matricea de adiacenta modificata in cazul 1-metil-2-propil-ciclopentanului [234].

Figura 70. Modul de constructie al 1 f si matricea de adiacenta modificata in cazul 1-metil-2-propil-ciclopentanului [234]
Valori optime pentru parametrii a si c sunt prezentate succint in referinta [233].
Indicele de conectivitate variabil 1 f a fost utilizat cu succes in modelari QSPR ale toxicitatii unor eteri alifatici [213] cand se obtine un coeficient de corelare r = 0.9548 sau in modelari QSPR ale punctelor de fierbere a 100 de alcooli [233] cand se obtine un coeficient de corelare r = 0.991.
3.3.2. Indicii de forma Kappa
Forma moleculara nu este usor de definit iar in situatia cand molecula este modelata printr-un graf notiunea de forma devine si mai difuza astfel incat era necesara introducerea unor descriptori care sa codifice forma moleculei. Acesti descriptori au fost construiti de catre Kier [236-239] prin examinarea formelor extreme ale grafului in doua situatii: i)graf-lant; ii)graf-stea Acesti indici de forma numiti si indicii kappa (k) reprezinta o masura a pozitiei relative a grafului fata de cele doua forme extreme. Aceste tipuri de indici se pot defini cu ajutorul ecuatiilor 159-161.
k = 21Pmax1Pmin / (1Pi)2 (159)
k = 22Pmax2Pmin / (2Pi)2 (160)
k = 43Pmax3Pmin / (3Pi)2 (161)
unde 1Pi, 2Pi, 3P3 reprezinta numarul de legaturi simple, duble respectiv triple; 1Pmin si 1Pmax reprezinta numarul de legaturi simple dintr-un graf liniar si complet; 2Pmin si 2Pmax reprezinta numarul de legaturi duble dintr-un graf liniar si graf stea; 3Pmin si 3Pmax reprezinta numarul de legaturi triple dintr-un graf liniar si graf stea-pereche.
Acesti descriptori de forma au fost testati in corelatii cu factorul acentric Pitzer cand se obtine un coeficient de corelare r = 0.995. Acest factor acentric definit [240] in termenii presiunii de vapori reduse masoara deviatia moleculei de la o forma sferica ideala.
Deoarece indicii kappa nu prezinta un grad de degenerare ridicat ulteriror au fost construiti noi tipuri de descriptori moleculari ai formei care prezinta astfel de degenerare [241].
3.3.3. Indicele Balaban J
In lucrarile sale [5, 23, 63, 242, 243] Balaban aplica formula de tip Randic (ec.154) sumelor de distante in locul valentelor varfurilor propunand noul indice topologic J denumit indicele de conectivitate al sumei distantelor medii:
J = (q/m S(sisj)-1/2 (162)
In ec.(162) m = q-N+1 reprezinta numarul ciclomatic al grafului cu q muchii si N noduri. Capacitatea de discriminarea acestui indice este mai mare ca a altor indici topologici [244]. Pentru alcanii cu catena foarte lunga valoarea indicelui J tinde catre = 3.14159 [245].
Sumarea din ecuatia 162 se face pe toate muchiile i-j intr-un graf fara hidrogen. In cazul legaturilor duble si triple sumarea se face luand in considerare ordinele de lagatura sau considerand legatura dubla ca doua legaturi simple iar legatura tripla ca trei legaturi simple.
Prezenta in molecula a heteroatomilor determina utilizarea unor parametrii speciali. In cazul matricea de distante D elementele diagonalei de definesc cu ajutorul ecuatiei 163 propuse de Trinajstic si colaboratorii [73]:
dii = 1 -6 / Zi (163)
unde Zi este numarul tuturor electronilor din atomul i. In Tabelul 19 sunt prezentate valorile dii pentru cele mai uzuale elemente.
|
Elemente |
C |
N |
O |
S |
F |
Cl |
P |
|
dii |
Tabelul 19. Valorile dii pentru cele mai uzuale elemente
In cazul elementelor nediagonale se utilizeaza ecuatia 164 :
dij = Σqkq = Σq36 / bqZiZj (164)
in care sumarea se face peste toate varfurile adiacente.
Ordinul de legatura definit initial de Balaban [63, 243] este 1 pentru legaturile simple, 2 pentru cele duble si 3 pentru cele triple.
In Tabelul 20 sunt prezentate valorile parametrului kq pentru cele mai uzuale legaturi intalnite in compusii chimici.
|
Legatura |
C=C |
C-C aromatic |
C=N |
C-N aromatic |
C-O |
C=O |
|
kq |
Tabelul 20. Valorile parametrului kq pentru cele mai uzuale legaturi intalnite in compusii chimici
O a doua metoda este propusa de Basak si colaboratorii [246] care utilizeaza teoria informationala si gruparea varfurilor in clase in functie de natura lor chimica dar fara sa se ia in considerare periodicitatea chimica.
Avand in vedere considerentele prezentate precum si valorile unei electronegativitati relative Xj, Balaban defineste [247] un nou indice topologic J pentru heteroatomi (JhetX) prin multiplicarea sumei distantei dj cu Xj si aplicarea formulei 162 pentru J.
Cum heteroatomii de diferentiaza si prin razele covalente se defineste si un al doilea indice topologic J pentru heteroatomi (JhetY) in aceeasi maniera ca JhetX utilizandu-se valorile razelor covalente relative [247].
Balaban arata [247] ca JhetY depinde de interactiile sterice astfel incat in cazul unor amine are valoarea cea mai scazuta in cazul aminelor primare, valoare medie in cazul celor secundare si valoare maxima in cazul aminelor tertiare deoarece atomul de N are raza covalenta mai mica ca cea a atomului de C. In cazul JhetX situatia este inversa adica valoarea cea mai mica este in cazul aminelor tertioare si cea mai mare in cazul aminelor primare. Pe de alta parte valorile JhetX si JhetY cresc cu cresterea ramificarii moleculelor.
Pentru calculul lui Jhet a fost scris un program software care tine cont de toti parametrii structurali ai molecului [248].
Domeniile de utilizare ale indicelui J sunt dintre cele mai variate. In studii recente indicele Balaban a fost utilizat cu succes in studii QSAR privind benzensulfonamidele ca inhibitori ai anhidrazei carbonice [249], sau pentru prezicerea cifrei octanice pentru o serie de alcani [158].
Pentru prezicere punctelor de fierbere si a coeficientului de partitie octanol-apa a fost realizat un model QSPR in care indicele J aduce o contributie sporita pentru marirea coeficientului de corelare r [160]. Indicele Balaban face parte din setul de descriptori utilizati pentru dezvoltarea unor relatii cantitative structura-activitate (QSAR) pentru prezicerea activitatii anticonvulsive in cazul unor analogi ai hidantoinei [250] sau in modelarea actiunii anticancer a unor derivati retinoidici [251].
El a fost aplicat cu bune rezultate in QSAR [252], pentru modelarea cantitativa a efectelor sterice in studiul potentialului carcinogenic al unor hidrocarburi aromatice polinucleare sau a mutagenicitatii pentru o serie de amine aromatice si heteroaromatice [161]. In studii de biodegradabilitate sau de toxicitate indicele J este utiliat cu succes pentru prezicerea toxicitatii policlorodibenzofurani [253]. In studii foarte recente indicele J isi gaseste aplicabilitatea si in prezicerea capacitatii de legare de diferiti receptori a unor policlorobifenili, policlorodibenzo-p-dioxine si policlorodibenzofurani utilizand date de 13C RMN [254].
Indicele J este utilizat mai recent si in modele QSAR pentru prezicerea activitatii biologice a diversilor compusi biologic activi sau potentialului de inhibare a unor compusi chimici precum ar fi modelul propus de S. C. Basak si colaboratorii [162] pentru prezicerea potentialului de inhibare a 107 benzamidine.
Indicele Balaban a fost utilizat si in studii QSPR pentru prezicerea unor proprietati ale compusilor chimici cum ar fi : presiunea de vapori [157] , punctele de fierbere in cazul eterilor aciclici, peroxizilor, acetalilor si analogi cu sulf [255], sau a unui set de 139 de hidrocarburi format din 73 de alcani C3-C9, 29 de alchilbenzeni si 37 de hidrocarburi aromatice policiclice [256] precum si entalpia de formare din elemente a unui set de 60 de hidrocarburi aromatice si nearomatice [62].
3.4. A treia generatie de indici topologici
Cea mai recenta generatie de indici topologici (a treia generatie) sunt numere reale si se bazeaza pe invarianti locali ai varfurilor care de asemenea sunt numere reale. Cele mai importante categori de astfel de indici sunt prezentate in cele ce urmeaza.
3.4.1. Indici teoretici informationali
Teoria informationala reprezinta un mod eficient de caracterizare a diferitelor structuri [257, 258]. Pentru un sistem I avand N elemente, continutul informational poate fi redat cu ajutorul ecuatiei 165 :
![]()
unde n este numarul de seturi diferite de elemente, Ni este numarul de elemente din setul i iar sumarea se face pe toate seturile de elemente.
O alta teorie utilizeaza continutul informational mediu pentru un element al unui sistem, Ī, care poate fi definit ca medie a continutului informational total sau cu ajutorul formulei Shannon:
![]()
in care pi = Ni /N.
Teoria informatiei a fost aplicata la grafuri pentru prima data in 1955 de catre Rashevsky [259] pentru definirea continutului informational topologic. Aceasta definitie se refera de fapt la impartirea varfurilor unui graf dat in clase de varfuri echivalente avand aceasi valenta.
Continutului informational topologic nu poate explica faptul ca ramificarea in cazul grafurilor lant creste in acelasi mod ca in cazul grafurilor stea sau arbore.
Pentru a inlatura aceste inconveniente Bonchev si Trinajstic aplica formula Shannon (ec. 166) pentru definirea [58] unor noi indici informationali derivati din matricea de distante D care sa cuprinda si cea ce nu poate explica teoria Rashevsky:
![]()
In care N(N-1) / 2 reprezinta numarul de elemente nediagonale din partea superioara a matricei de distante iar ki reprezinta numarul de elemente avand aceeasi valoare i.
Aplicand ecuatia 166 se poate defini [58] si un indice informational mediu:
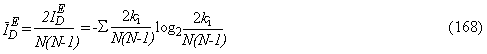
In referinta [58] sunt prezentate expresiile analitice ale indicilor informationali pentru toate categoriile de grafuri.
Acesti indici informationali reprezinta asadar o modalitate eficienta de a exprima ramificarea structurilor chimice (grafurilor moleculare caracteristice).
Indicii informationali dezvoltati de Basak si colaboratorii
Deoarece atomii de hidrogen dintr-o molecula isi au rolul lor, Basak si colaboratorii definesc [260-262] continutul informational al moleculei cu ajutorul unui indice IC :
![]()
Indicele de ordin 0 se refera la atomi izolati grupati in clase echivalente iar cel de ordin 1 se refera la perechi de atomi legati covalent grupati in seturi cu aceeasi echivalenta. Setul de n varfuri este partitionat pana la vecini de ordinul k.
A doua categorie de indici informationali se numesc indici informationali structurali si se pot defini cu ajutorul ecuatiei 170:
SICk = ICk / log2n (170)
A treia categorie de indici informationali definiti de Basak si colaboratorii poarta numele de indici informationali complementari si se pot prezenta cu ajutorul ecuatiei 171:
CICk = log2n - ICk (171)
3.4.3. Indicele informational orbital
In baza teoriei informationale si utilizand un invariant m(oricare ar fi acesta) al grafului, Bertz defineste [263] un indice C(m) utilizand formula Shannon modificata de Rashevsky si Mowshowitz. Acest indice este aplicat si la grafuri ce contin heteroatomi si legaturi multiple:
C(m) = 2mlog2m - imilog2mi (172)
3.4.4. Indici topologici bazati pe informatia data de distante
In cazul alcanilor, odata cu cresterea numarului atomilor de carbon creste si numarul izomerilor iar o metoda bruta de insumare a distantelor din graful respectiv conduce la pierderea informatiei continuta in secventa de distante de la un varf dat la altul din graful dat.
Pentru a inlatura aceste inconveniente, Balaban utilizand formula Shannon propune [264] noi invarianti ai varfurilor care se bazeaza pe secventa de distante topologice. Aceasta secventa de numere (distante topologice) a fost utilizata de Bonchev si Trinajstic pentru constructia altor indici topologici [265, 266].
Balaban aplica formula Shannon la continutul informational in vectori distante, pentru fiecare varf i obtinand informatia locala medie exprimata ca lungimea distantelor, ui:
ui i(jgj) / (si)log2j/si (173)
unde :
si = jdij jjgj (174)
iar j reprezinta toate distantele avand exponentul gj.
De asemenea se poate obtine si informatia locala exprimata ca lungimea distantelor, vi:
vi = silog2si - ui (175)
Pentru a se obtine o secventa de numere mai convenabila au fost de asemenea propusi alti invarianti locali ai varfurilor care prin analogie cu cei definiti in ecuatiile 173 si 175 au fost denumiti ca informatie locala extinsa exprimata ca lungimea distantelor, xi, respectiv informatia locala extinsa medie exprimata ca lungimea distantelor, yi:
xi = silog2si - yi (176)
yi jgjjlog2j (177)
Cu ajutorul invariantilor locali ai varfurilor definiti cu ajutorul ecuatiilor 173, 175, 176 si respectiv 177 se pot defini [264] indicii topologici corespunzatori:
U = (q / (uiuj)-1/2 (178)
V = (q / (vivj)-1/2 (179)
X = (q / (xixj)-1/2 (180)
Y = (q / (yiyj)-1/2 (181)
Sumarea se face peste toate muchiile ij, q respectiv reprezentand numarul de muchii respectiv cicluri din graf. se mai numeste si numar ciclomatic : = q + 1 - n.
Aceste tipuri de indici au fost propuse pentru a se reduce degenerarea indicilor topologici la nivel global si foarte putin la nivel local. Degenerarea acestor indici e mult mai mica ca a indicelui J fiind utilizati pentru caracterizarea familiilor de izomeri ai alcanilor.
3.4.5. Indicii TRIPLET
Indicii triplet convertesc o matrice intr-un sistem de ecuatii liniare a caror solutii sunt invariantii locali ai varfurilor prin includerea unui vector coloana pe diagonala principala si a altui vector coloana ca termen liber.
Acest vector coloana poate exprima informatia chimica (de exemplu numarul atomic Z al unui atom simbolizat prin varful corespunzator), informatia teoretica codata de un graf (de exemplu gradul unui varf V sau suma distantei S pentru un varf corespunzator) sau simple constante numerice (de exemplu numarul 1, numarul de varfuri N sau N2) [ 129, 262].
Invariantii locali ai varfurilor xi sunt convertiti in descriptori moleculari prin unul din urmatorii cinci operatori:
Insumarea: ∑i xi
Insumarea patratelor : ∑i xi2
Insumarea radacinilor patrate: ∑i xi-½
Insumarea radacinilor patrate: ∑ij (xixj)-½
Produsul mediu: N( i xi)1/N
Cu ajutorul operatiilor 1-5 se pot obtine indicii topologici triplet [267].
|