Efectul fotoelectric.

Efectul fotoelectric.

Planck a postulat ca oscilatorii din peretii unei cavitati au energiile cunatificate, dar a tratat radiatia electromagnetica ca o distributie cuntinua de energie, ca īn teoria clasica a electromagnetismului.

Pentru a explica efectul fotoelectric, Einstein a presupus ca si radiatia electromagnetica consta din "pachete" de energie (sau, cuante de energie) si a considerat o unda electromagnetica ca fiind formata din cuante de energie , (unde este frecventa undei) numite fotoni. Cu acest nou concept, lumina poate fi considerata un "fascicol de fotoni".

Efectul fotoelectric a fost descoperit de Hertz, care a 949h710j observat ca daca lumina ultravioleta cade pe o suprafata metalica, se produc scāntei. Experiente ulterioare au aratat ca la impactul luminii pe o suprafata metalica, se expluzeaza electroni.

Schema dispozitivului experimental pentru studierea efectului fotoelectric este urmatoarea (Fig. 3.16): un tub vidat cu catodulul K si anodulul A polarizati cu tensiunea V. Lumina de la o lampa lumineaza catodul, electronii extrasi din metal pot ajunge la anod, ducānd la aparitia unui fotocurent I īn circuitul exterior.

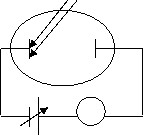
Figura 3.16

S-a observat ca īn cazul polarizarii directe (V>0), la cresterea tensiunii V, fotocurentul I creste pāna la o valoare de saturatie, cānd toti electronii emisi de catod ajung la anod (Fig. 3.16). Inversānd polaritatea (catodul - pozitiv, anodul - negativ), fotocurentul I scade si la o anumita valoare a tensiunii de polarizare, -V₀, fotocurentul se anuleaza.

Figura 3.17

De asemenea, fotocurentul creste cu intensitatea radiatiei, īn concordanta cu teoria clasica conform careia numarul de electroni emisi īn unitatea de timp este proportional cu intensitatea radiatiei incidente.

Valoarea tensiunii -V₀ pentru care fotocurentul se anuleaza corespunde unei energii potentiale a cāmpului dintre catod si anod care anuleaza energia cinetica maxima a electronilor:

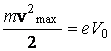(3.48)

Potentialul V₀ pentru care se realizeaza conditia de mai sus se numeste potential de frānare (stopare).

Din datele experimentale se pot trage urmatoerele conluzii, care constituie legile efectului fotoelectric:

Exista o frecventa limita , numita frecventa de prag,

caracteristica fiecarui material, sub care nu are loc efectul fotoelectric. Conform teoriei clasice, emisia electronilor ar trebui sa aiba loc la orice frecventa, daca intensitatea luminii este suficient de mare si expunerea are loc suficient de mult timp.

Potentialul de stopare V₀ (si deci, energia cinetica maxima

electronilor) depinde liniar de frecventa radiatiei incidente si nu depinde de intensitatea radiatiei. Conform teoriei clasice, a electronilor emisi ar trebui sa creasca cu densitatea de energie (adica, cu intensitatea radiatiei).

Efectul fotoelectric este instantaneu. In teoria clasica, energia luminoasa

este distribuita uniform pe frontul de unda si ar trebui sa se concentreze pe o suprafata de ordinul dimensiunii atomului, ceea ce ar necesita un oarecare timp.

In 1905 Einstein, generalizānd postulatul lui Planck asupra luminii, a explicat legile efectului fotoelectric, introducānd notiunea de foton. Fotonii sunt bine localizati īn spatiu, astfel īncāt toata cuanta de energie este absorbita de atom la un moment dat, pentru a expulza electronul. O parte din aceasta energie, W, este necesara electronului pentru a parasi metalul si se numeste lucru de extractie al electronilor din metal. Restul, se regaseste sub forma de energie cinetica a electronului. Adica,

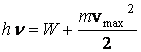(3.49)

Lumina cu intensitate mai mare scoate mai multI electroni din metal, dar nu cedeaza fiecarui electron mai multa energie.

Ecuatia de mai sus este cunoscuta ca ecuatia Einstein.

Frecventa de prag este acea frecventa pentru care

(3.50)

Din relatiile (3.48) si (3.49) rezulta ca potentialul de frānare creste liniar cu frecventa (Fig. 3.18):

(3.51)

Figura 3.18

Numarul de fotoelectroni emisi este proportional cu numarul de fotoni care cad īn unitatea de timp pe o anumita suprafata, fiecare foton avānd energia . Cum intensitatea radiatiei este proportionala cu numarul de fotoni, fotocurentul este proportional cu intensitatea radiatiei.

Efectul fotoelectric are astazi multe aplicatii practice la detecta luminii cu dispozitive electronice foarte sensibile. Un exemplu este fotomultiplicatorul (un tub cu mai multi electrozi, electrozii secundari fiind numiti dinode) (Fig. 3.19).

Fig. 3.19

Un foton incident scoate din catod un electron, care este accelerat spre un electrod secundar. La impactul cu acesta scoate cātiva electroni, care sunt accelerati spre alt electrod secundar de unde fiecare scoate cātiva electroni si asa mai departe, se genereaza o avalansa de electroni. Intr-un fotomultiplicator de tensiune ridicata se pot genera pāna la electroni, adica un curent detectabil. Un astfel de fotomultiplicator poate detecta prezenta unui foton, pe acest principiu construindu-se camere TV foarte sensibile.

Spectrele atomice si modelul Bohr pentru atomul de hidrogen.

Newton a fost primul care a descompus lumina alba īn culorile componente folosind prisma optica. Īn 1792, T. Melvill a aratat ca lumina unui gaz incandescent este formata dintr-un numar mare de frecvente discrete, numite linii de emisie (pe o placa fotografica apar ca niste linii).

S-a descoperit, de asemenea, ca daca se iradiaza atomi cu un fascicul luminos cu spectru continuu, analiza fascicolului dupa iradiere arata prezenta liniilor de absorbtie (īntunecate), corespunzatoare frecventelor de emisie ale atomilor respectivi.

Kirchhoff (1859) a aratat ca pentru fiecare element, spectrul de emisie coincide cu cel de absorbtie, altfel spus, fiecare element are un spectru de linii caracteristic.

Balmer (1885) a observat o anumita regularitate īn spectrul de linii īn vizibil si UV. Aceste linii, notate formeaza seria Balmer si au lungimea de unda astfel īncāt

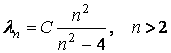(3.52)

unde valoarea constantei este A

Rydberg (1889) a scris liniile seriei Balmer cu ajutorul numarului de unda , sub forma:

(3.53)

Constanta se numeste constanta Rydberg.

Relatia de mai sus se poate generaliza si īn cazul altor serii spectrale:

(3.54)

Diferitele serii spectrale se obtin fixānd n_a   si dānd valori n_b>n_a:

Pentru se obtine seria Lyman (UV)

Pentru se obtine seria Balmer (vizibil)

Pentru se obtine seria Pascher IR

Pentru se obtine seria Bracket IR

pentru se obtine seria Pfundt IR

In general, numarul de unda al unei linii spectrale se scrie sub forma

unde sunt termeni spectrali:

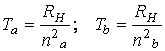
Pentru alti atomi, termenii spectrali au o forma mai complicata.

Rezulta ca un spectru atomic este caracterizat de un set de termeni spectrali. Daca numerele de unda pentru trei linii spectrale sunt:

rezulta ca

(3.55)

Aceasta relatie este constituie principiul de combinare Ritz.

Existenta acestor linii spectrale nu poate fi explicata folosind modelele fizicii clasice.

N. Bohr (1913), combinānd modelul Rutherford pentru atom (Rutherford a efectuat o experienta de īmprastiere de particule pe folii de Al, īn urma careia a concluzionat ca toata sarcina pozitiva si aproape toata masa atomului sunt concentrate īn nucleu), conceptul de cuanta introdus de Planck si de foton introdus de Einstein, a obtinut un model atomic care putea explica linii spectrale.

Bohr a presupus ca electronul atomului de hidrogen se misca pe o orbita circulara īn jurul nucleului. Pentru obtinerea energilor si razelor permise ale electronului a postulat:

1) Orbitele si energiile electronului īn atom sunt cuantificate, adica sunt permise doar anumite valori discrete. Un electron pe o astfel de orbita este īntr-o stare stationara.

Electronul poate efectua tranzitii īntre doua stari stationare, tranzitii īn urma carora emite sau absoarbe energie.

2) Miscarea electronului pe aceste orbite stationare este descrisa de legile mecanicii clasice, dar care nu poate explica tranzitiile.

3) La o tranzitie īnte doua stari stationare, electronul emite un foton de energie si frecventa ,

,

daca . Daca , electronul absoarbe energie.

4) Orbitele permise sunt caracterizate de valori discrete ale momentului

cinetic orbital

(3.56)

"n" se numeste numar cuantic principal si ia valorile īntregi,

Modelul se poate aplica atomilor hidrogenoizi (ioni cu un singur electron: ) si permite calcularea energiilor si razelor permise ale electronului.

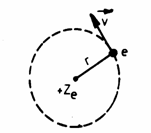
Fig. 3.20

Presupunem ca (Fig. 3.20):

orbitele sunt circulare

nucleul este infinit greu fata de electron.

miscarea electronului pe orbita este nerelativista.

Electronul se afla īn cāmpul coulombian al nucleului si din egalitatea fortelor care actioneaza asupra lui si postulatul (4) rezulta:

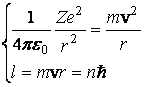(3.57)

unde m este masa electronului.

Din (3.57) se obtin valorile permise ale vitezelor electronului pe o orbita stationara , viteze care sunt cuantificate:

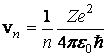(3.58)

Razele permise ale orbitelor sunt:

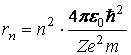(3.59)

Cea mai mica raza pentru atomul de hidrogen se numeste raza Bohr, si are valoarea

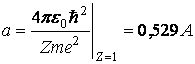(3.60)

Energia electronului aflat pe orbita de raza este

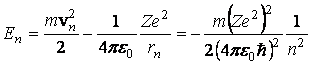(3.61)

Deoarece , starile legate ale atomului unielectronic sunt discrete, spectrul energetic este format dintr-un numar infinit de nivele de energie discrete.

Starea cu cea mai joasa energie se numeste stare fundamentala, ; celelalte stari, n>1, se numesc stari excitate.

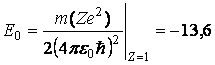eV (3.62)

Diagrama energetica a nivelelor permise ale atomului de hidrogen este (Fig. 3.21):

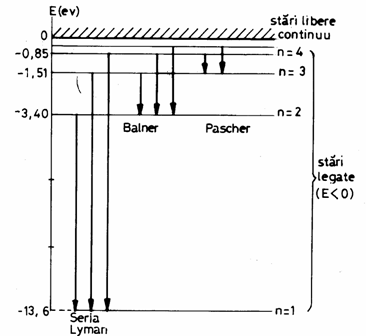
Fig. 3.21

Din relatia

rezulta

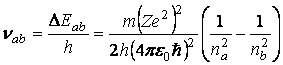
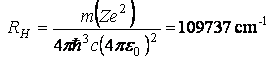
ceea ce conduce la urmatoarea valoare pentru constanta Rydberg

valoare foarte apropiata de cea data de Rydberg.

Energia starii n se poate scrie sub forma

(3.63)

cu

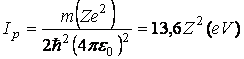
I_p se numeste potential de ionizare si reprezinta energia necesara scoaterii unui electron din starea fundamentala (n=1) si a deveni liber (nelegat de atom).

Daca electronul este īntr-o stare legata (E_n <0) si primeste o cantitate de energie mai mare decāt energia de legatura, va fi expulzat din atom si va deveni liber, avānd o energie pozitiva.

Rezulta ca starile de energie pozitiva corespund starilor īn care electronul este liber (nu mai este legat de nucleu), starile nelegate putānd avea orice valoare pozitiva. Spectrul starilor nelegate este continuu, pe cānd al celor legate este discret. Tranzitiile pot avea loc atāt īntre starile legate din spectrul discret, cāt si īntre o stare legata si una libera, sau īntre doua stari din spectrul continuu (tranzitii liber-liber).

3.6. Demonstratia lui Einstein pentru densitatea spectrala de energie.

Planck a obtinut o formula corecta pentru densitatea spectrala de energie folosind cuantificarea energiei emise de atomii din peretii cavitatii īn care se afla radiatia, dar a folosit numarul de moduri de oscilatie din electromagnetism . Demonstratia lui Planck foloseste cuantificarea energiei , dar porneste de la formula

unde este energia medie a unui oscilator.

Einstein a propus o demonstratie alternativa pentru densitatea spectrala de energie, bazata pe modelul Bohr.

Se considera un sistem cu N atomi, fiecare atom cu doua nivele energetice si , populate cu respectiv , (Fig.3.22)

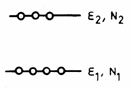
Fig. 3.22

La echilibru termic, sistemul este descris de statistica Maxwell-Boltzmann:

(3.64)

Vom analiza interactia dintre acest sistem si radiatia electromagnetica de frecventa n si densitate de energie electromagnetica , interactie care se poate manifesta prin:

1) Absorbtia radiatiei

2) Emisia spontana

3) Emisia stimulata

1) Absorbtia este procesul prin care un atom aflat īn starea fundamentala, absoarbe un foton de frecventa si trece pe nivelul superior (Fig.3.23). Rata de absorbtie (numarul de tranzitii īn unitatea de timp de pe ) este:

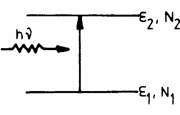
Fig. 3.23

(3.65)

unde:  este densitatea spectrala a energiei radiatiei

se numeste coeficientul Einstein de absorbtie

este probabilitatea de absorbtie

2) Emisie spontana este realizata īn absenta radiatiei externe si consta īn tranzitia de pe nivelul excitat pe nivelul fundamental (Fig. 3.24). Radiatia emisa este de frecventa si poate fi radiativa necoerenta (procesele de emisie spontana nu sunt corelate īntre ele), sau poate fi neradiativa (se cedeaza atomilor din jur). Frecventa radiatiei emise este

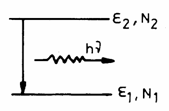
Fig. 3.24

Rata de emisie spontana este

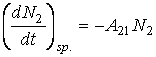(3.66)

unde :  se numeste coeficientul Einstein de emisie spontana;

este probabilitatea de emisie spontana

Prin integrarea relatiei (3.66) se obtine ca prin emisie epontana, numarul atomilor scade exponential:

(3.67)

Marimea 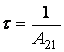se numeste timp mediu de viata pe nivelul 2.

3) Emisia stimulata.

Daca atomul se afla pe nivelul excitat si o unda electromagnetica de frecventa

cade pe material, exista o probabilitate finita ca radiasia sa forteze atomul sa efectueze tranzitia . Radiatia emisa va fi īn faza cu unda incidenta.

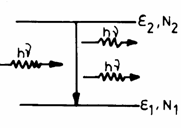
Fig. 3.25

Rata de emisie stimulata va fi

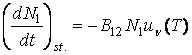(3.68)

unde   este coeficientul Einstein de emisie stimulata

reprezinta probabilitate de emisie stimulata

Echilibrul radiatiei este realizat cānd numarul proceselor absorbite este egal cu numarul proceselor de emisiei:

(3.69)

Tinānd cont de relatia (3.64), rezulta ca densitatea spectrala de energie este

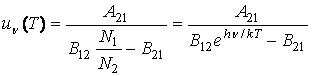(3.70)

Deoarece experimental se constata ca

De asemenea,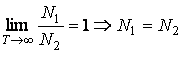

ceea ce conduce la egalitatea coeficientilor de emisie stimulata si de absorbtie:  (3.71)

Rezulta ca densitatea spectrala de energie are expresia

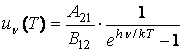(3.72)

Comparānd cu relatia Rayleigh-Jeans valabila la lungimi de unda mari (deci mici), ,

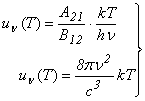
rezulta

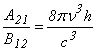
si, īn final se obtine pentru densitatea spectrala de energie expresia

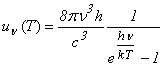(3.73)

adica aceeasi cu cea obtinuta de Planck.

3.7. Aplicatie: Laseri.

Vom considera un sistem atomic cu doua nivele de energie nedegenerate , , populatiile nivelelor fiind la , respectiv , care este luminat cu o radiatie de densitate si frecventa .

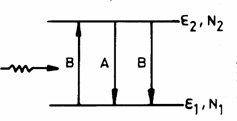
Fig. 3.26

Tinānd cont de relatia (3.72)

variatia populatiilor celor doua nivele va fi:

adica

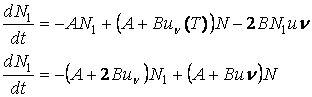(3.74)

Ecuatia omogena:

are solutia

iar solutia ecuatiei neomogene va fi:

(3.75)

La fel pentru a doua ecuatie (3.74):

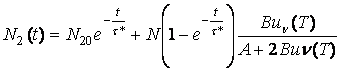(3.76)

Īn limita , populatiile celor doua nivele devin:

(3.77)

Daca pompajul este foarte intens, procesele de emisie spontana se neglijeaza, si atunci

(3.78)

adica, populatiile celor doua nivele se egalizeaza, spunem ca tranzitia se satureaza.

3.7.1.Inversia de populatie. Absorbtia radiatiei.

Daca o unda monocromatica de frecventa si intensitate cade pe un strat omogen de substanta, este absorbita o parte din radiatie (Fig. 3.27)

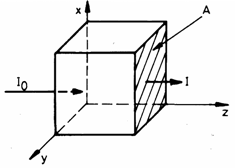
Fig. 3.27

la iesirea din stratul de material de grosime z intensitatea undei fiind

(3.79)

unde este coeficientul de absorbtie īn material.

Daca:

In al doilea caz, radiatie este amplificata.

Neglijānd emisia spontana (īn cazul pompajului intens), variatia energiei absorbita de la radiatie īn unitatea de timp si unitatea de volum este

; (3.80)

unde este intensitatea spectrala a radiatiei cu frecventa

Dar, neglijānd emisia spontana, energia absorbita de la cāmp īn unitatea de timp, pe unitatea de volum, este

_{Rezulta ca}

(3.81)

unde

Din (3.80) si (3.81) rezulta

adica intensitatea spectrala a radiatiei scade exponential cu z:

_(3.82)

unde coeficientul de absorbtie este

(3.83)

Daca ,coeficientul de absorbtie este negativ si se obtine amplificarea radiatiei.

Trebuie, deci, sa se realizeze conditia , adica inversie de populatie, care se poate obtine prin pompaj (optic, electronic, injectie de purtatori, radiatii ionizate) īntr-un sistem cu 3 nivele energetice.

3.7.2. Laserul cu rubin

Rubinul roz () impurificat cu , are urmatoarea diagrama energetica:

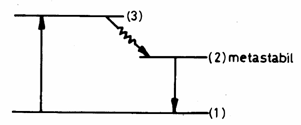
Fig. 3.28

O radiatie cu (verde) excita ionii de pe nivelul (1)pe nivelul (3). Daca se neglijeaza tranzitiile spontane (3) (1), ramān tranzitiile (3)

Daca timpul de viata al starii (2) este foarte lung, pe acest nivel de energie se acumuleaza ioni, astfel ca īn timp se realizeaza inversia de populatie īntre nivelele (1) si (2).

Cānd este īndeplinita conditia de prag

;

unde este un coeficient care descrie pierderile īn mediu

este timpul de viata pe nivelul (2)

are loc emisia radiatiei cu lungimea de unda

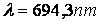(3.84)

(rosu) si se obtine un semnal laser. Nivelul metastabil (2) se goleste si trebuie repopulat. Se obtine īn acest fel un semnal laser sub forma de impulsuri scurte (cu durata de ).