CARACTERIZAREA SISTEMELOR LINIARE SI INVARIANTE IN DOMENIUL COMPLEX TEORIA SISTEMELOR

CARACTERIZAREA SISTEMELOR LINIARE  SI INVARIANTE ĪN DOMENIUL COMPLEX.

8.1. INTRODUCERE

Acest mod de caracterizare a relatilor intrare-iesire a unui sistem utilizeaza imaginile operationale ale marimilor de intrare si iesire:

U₁(S),U₂(S),.,U_r(S) si Y₁(S),Y₂(S),.,Y_m(S)  unde S este variabila complexa: S=t jw

Relatiile intrare-iesire dintre diferitele per 939c28j echi de marimi de intrare-iesire se exprima prin functii rationale de variabila complexa S numite functii de transfer:

Sau matricial:

8.2. TRANSFORMATA LAPLACE A FUNCŢILOR DE VARIABILĂ REALĂ

Transformata (imaginea) operationala Laplace F(S) a unei functii de variabila reala f(t), daca exista este data de integrala:

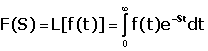
Conditile pentru care o functie f(t) numita si "original" sa aiba imagine sunt urmatoarele:

f(t):R R este nula pentru t<0

f(t) este derivabila pe portiuni: [0,t₁],[t₁,t₂],.[t_n,

functia f(t) are un ordin de crestere marginit daca daca exista numarul M asfel īncāt f(t)<Me^Ct. cu C "indice de crestere" al functiei f(t).Se poate demonstra ca daca functia f(t) respecta conditile 1-3, functia imagine (transformata Laplace) a ei este definita in planul R_es>C (vezi fig. 8.1).

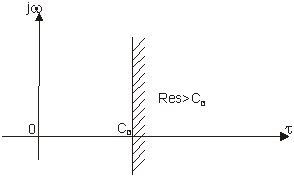
fig. 8.1

Exemplul 1:

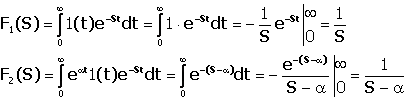
Sa se gaseasca functia imagine pentru urmatoarele functii: functia treapta unitara f₁(t)=1(t) si f₂(t)=e^at1(t)

8.3. CALCULUL FUNCTILOR ORIGINAL

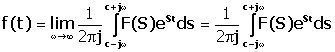
Daca F(S)=L(f(t)), iar C este indicele de crestere al functiei f(t), atunci īn punctele unde f(t) este continua ea este data de relatia:

Pentru ca o functie sa aiba "original" este necesar ca:

functia F(S) sa fie olomorfa īn semiplanul (S Res cu S>C)

functia F(S) sa tinda uniform catre 0 īn raport cu argumentul S cānd S

Integrala din definitie este absolut convergenta

Se poate demonstra īn baza teoremei lui Cauchy si a rezidurilor ca relatia de definitie poate fi exprimata si cu:

Unde S_K sunt variabilele care anuleaza numitorul (polii) functiei F(S)e^St.

Calculul reziduriilor R_es se face īn felul urmator:

a)     pentru poli simpli

b)    

pentru poli multipli S_m de un ordin oarecare p

Exemplul 2: Sa se determine originalul f(t) al functiei imagine F₁(S)

Exemplul 3: Sa se determine originalul f(t) al functiei imagine F₂(S)

Se calculeaza polii (radacinile) numitorului functiei S²+S+1=0, 

Vom avea:

8.4. PROPRIETATILE TRANSFORMATEI LAPLACE

8.4.1. TRANSFORMATA (IMAGINEA LAPLACE) A FUNCŢIILOR CU DISCONTINUITĂŢI.

Cunoscānd expresila functiei īn intervalele de continuitate:

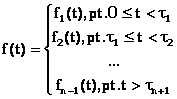
functia imagine poate fi gasita cu relatia: L[f(t)]=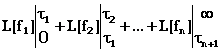

Exemplul 4: Sa se determine imaginea functiei definite grafic īn fig. 8.2.

Expresia analitica a functiei considerate este:

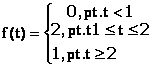
din formula de calcul vom avea:

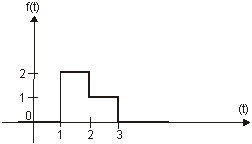
fig. 8.2

L[f(t)]=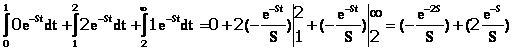

8.4.2. TRANSFORMATA (IMAGINEA LAPLACE) DERIVATEI UNEI FUNCTII.

Pentru calcul se utilizeaza relatia: L[f⁽ⁿ⁾(t)]=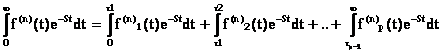 sau

L[f⁽ⁿ⁾(t)]= SⁿF(S)-S^n-1f(0)-S^n-2f'(0)-S^n-3f''(0)-.-f^(n-1)(0) - teorema derivatei-

Exemplul 5: Sa se determine imaginea derivatei de ordin 1 a functiei:

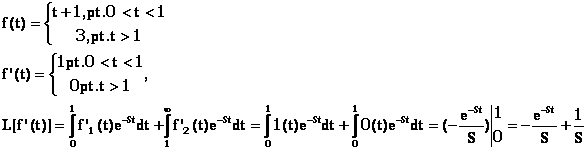
8.4.3. TRANSFORMATA (IMAGINEA LAPLACE) INTEGRALEI  UNEI FUNCTII.

Pentru calcul se utilizeaza relatia: L[f^(-n)]= cu F(S)=L[f(t)] si