GRAFURI - Manualul profesorului

Clasa a XI-a

GRAFURI

NOTIUNI INTRODUCTIVE

Manualul profesorului

Cuprins

Terminologie

Informatii generale despre tema prezentata

Obiective

Structura generala

Continut

Recomandari de structurare si predare

Structura detaliata a continuturilor

Introducere - Drumul lui Napoleon

Constructie - Istoricul grafurilor

Incidenta

Graf partial

Subgraf

Graf bipartit

Graf complet

Graf conex

Teste de evaluare

Teme pentru acasa

Bibliografie
Terminologie - Prezentarea elementelor de software

Obiect de continut

Un fisier independent, care prezinta informatii grupate din punct de vedere tematic, ce nu pot fi prezentate separat. Poate fi format din mai multe pagini de continut .

In cadrul acestui ghid vom folosi si notiunea de componenta atunci cand vom face referire la un obiect de continut.

Butoane Start animatie / Trecem la pasul urmator

Sunt amplasate in cadrul animatiilor si al aplicatiilor care contin mai multi pasi. Prin apasarea acestui buton se trece la pasul urmator al animatiei.

Butonul Reluare animatie

Este amplasat in cadrul animatiilor si prin accesarea acestuia se poate relua animatia.

Butonul de obiective

Este amplasat in partea de jos a ecranului si ofera utilizatorului, intr-o fereastra de detalii, obiectivele parcurgerii materialului din modulul respectiv.

Buton Trecem la pasul anterior

Este amplasat in cadrul teoriei si prin accesarea acestui buton se revine la jocul interactiv care a utilizat teoria respectiva.

Butonul Teorie

Prin accesarea acestui buton se ofera elevului posibilitate 525t198f a de a revedera notiunile teoretice necesare rezolvarii interactive a preoblemei amintite.

Butonul Help

Se afla amplasat in partea dreapta sus a ecranului. Prin accesarea acestui buton se deschide fereastra Help care ofera indicatii despre modul de utilizare a mouse-ului in desfasurarea jocului interactiv propus.

Buton de Demonstratie

Prin accesarea acestuia se ofera elevului demonstrarea unei anumite teoreme din teoria grafurilor, teorema care este enuntata si urmata apoi de butonul de demonstratie.

Buton de Constructie

Este plasat in partea din dreapta jos a ecranului .

Prin accesarea acestui buton se poate trece la momentul construirii unui graf. Se ofera elevului posibilitate 525t198f a de verificare interactiva a nivelului de intelegere a notiunii de graf.

Buton de Verificare / Resetare

Ofera posibilitatea de verificare a modului de rezolvare a unei cerinte de catre elev si respectiv reluarea rezolvarii problemei daca elevul acceseaza butonul Resetare.

Ferestre de meniuri

Sunt utilizate in cadrul construirii de grafuri neorientate. Aceste ferestre ofera elevului posibilitate 525t198f a de a construi nodurile si muchiile pentru un graf neorientat, precum si posibilitatea de a determina anumite marimi specifice cum ar fi : gradul unui varf

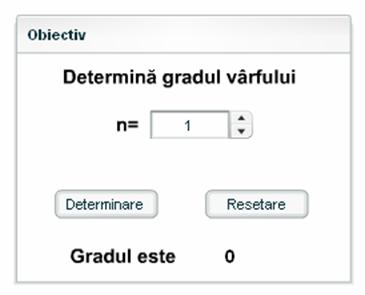
Ferestre mesaj

Se deschid in urma realizarii unei anumite sarcini de catre elev sau in urma comiterii unei greseli de catre elev. In aceasta fereastra se indica subiectului aprecierea rezultatului sau/si se dau eventual informatii suplimentare.

Buton de pauza

Prin accesarea acestui buton se opreste animatia pentru a observa mai multe detalii.

Fereastra de detalii

Aceasta fereastra ofera informatii suplimentare sau detalii despre un anumit element, termen, concept, imagine, personalitati, etc.)

2. Informatii generale pentru tema prezentata

Produsul informatic realizat ofera posibiliatea includerii in didactica de predare a teoriei grafurilor, a unor mijloace de invatare si comunicare performante, prin utilizarea calculatorului.

In acest mod procesul de predare - invatare este "personalizat", pentru fiecare elev in parte, avand in vedere particularitatile psiho-individuale si psiho-sociale ale acestuia.

In cadrul temei tratate - grafuri - notiuni introductive - au fost puse in evidenta urmatoarele aspecte :

Definirea notiunii de graf , cu accent pe problemele practice care se pot reprezenta prin grafuri ;

Prezentarea terminologiei legate de teoria grafurilor si antrenarea elevului in intelegera acesteia odata cu formarea unui vocabular de specialitate. ;

Folosirea unor metode activ - participative de tip "joc " pentru implicarea afectiva a elevului in procesul de invatare ;

Adaptarea lectiei la ritmul de invatare, atentiei si oboselii fiecarui subiect

Cuvintele cheie la aceasta tema sunt : graf, incidenta , grad, graf complet, graf bipartit, graf conex, lant.

Materialul are o structura modulatizata, care permite folosirea in mai multe variante a instrumentelor puse la dispozitie.

Momentele de evaluare faciliteaza munca profesorului in realizarea unui feedback continuu, permanent, corectiv.

3. Obiective

4. Structura generala

4.1 Continut

Se prezinta lista obiectelor de continut (notate cu M ) si carateristicile lor generale .

4.2. Recomandari de structurare si predare

Imbinarea modulelor realizate pentru aceasta lectie este la latitudinea fiecarui profesor, in functie de particularitatile psiho-individuae ale clasei.

Lectia 1 (Notiuni introductive in teoria grafurilor)

Lectia 2 (Tipuri de grafui)

5. Stuctura detaliata a contnutului

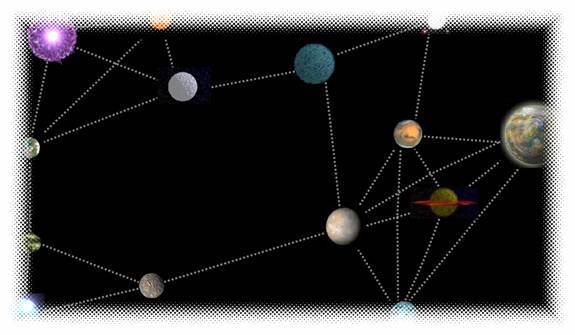
5.1. Introducere - Drumul lui Napoleon

Este un obiect interactiv care se prezinta sub forma de joc . Elevul trebuie sa gaseasca drumul pe care trebuie sa-l parcurga Napoleon din orasul Nancy pana la Viena. Se stie cati soldati poate pierde Napoleon daca parcurge un traseu sau altul.

Se cere elevului sa determine drumul dintre Nancy si Viena astfel incat sa se piarda un numar minim de soldati. Este un exemplu practic de utilizare a grafurilor.

Folosind butonul (resetare) jocul poate fi reluat.

Prin parcurgerea acestui modul se pune in evidenta o succesiune de operatii mintale care conduc elevul la descoperirea notiunii de graf.

5.2. Constructie -Istoricul grafurilor

Acest obiect familiarizeaza elevul cu notiunea de graf. Obiectul este interactiv si se prezinta pentru inceput sub forma unui joc "problema celor sapte poduri din orasul Kaliningrad".

Aceasta problema celebra a fost enuntata de matematicianul Euler, care impreuna cu Hamilton au fost cei care au pus bazele teoriei grafurilor. Punand mouse-ul pe cuvintele Euler si respectiv Hamilton se deschide o fereasta in care elevul afla mai multe detalii despre cei doi matematicieni.

In partea de jos a ecranului , prin apasarea pe cuvintele Legile lui Kirchoff si respectiv reprezentarea unor harti se face link la doua pagini distincte care dau explicatii asupra unor aplicatii practice a teoriei grafurilor.

In partea de jos a ecranului, dreapta, se afla doua butoane importante:

Definitie - prin accesarea acestui buton se trece la prezentarea definitiei notiunii de graf. Animatia folosita conduce si mai bine la intelegerea acestei definitii. In acest moment in patea de jos a ecranului exista doua butoane care au semnificatia () inainte, respectiv () inapoi.

Constructie - prin accesarea acestui buton se trece la constructia interactiva a unui graf cu noduri si muchii prestabilite Elevul are la dispozitie trei ferestre de meniuri cu care construieste nodurile, muchiile si verfica , respectiv reseteaza, rezolvarea cerintei, daca aceasta s-a facut gresit , sau daca elevul doreste sa reia problema.

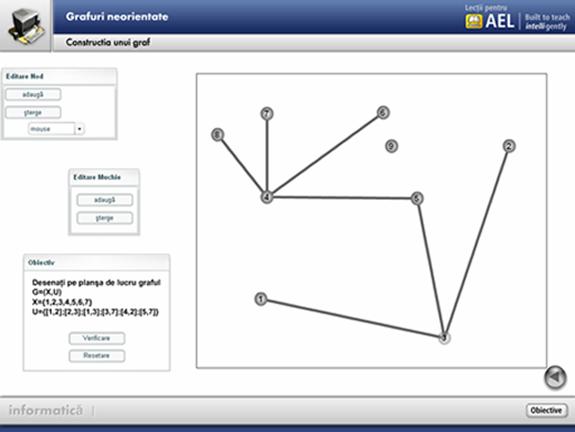
5.3. Incidenta

Acest modul este interactiv. In definirea notiunilor elementare legate de graf , se pleaca de la un joc, pe care elevul il are descris in partea stanga-sus a ecranului.

Prin participarea efectiva a elevului la rezolvarea jocului acesta se familiarizeaza cu notiunile teoriei grafurilor: incidenta, grad, adiacenta.

In partea de jos-dreapta a ecranului se afla doua butoane:

-La accesarea acestui buton se dau explicatii legate de gradul unui graf. In acelasi context este enuntata o teorema a carei demonstratie este data prin accesarea butonului .

- La accesarea acestui buton se dau explicatii legate de notiunile de adiaenta, incidenta.

5.4. Graf partial

Acest obiect este interactiv si are ca scop familiarizarea elevului cu notiunea de graf partial.

Pentru antrenarea optima a elevului la insusirea cunostintelor, modulul incepe cu un "joc - problema " care cere determinarea unui graf partial obtinut prin eliminarea unui numar optim de muchii astfel incat un turist sa poata vizita oricare cabana.

Folosind aceasta metoda activ-participativa , elevul nu asimileaza "mecanic" notiunea, ci beneficiaza direct de intelegerea logica a ei.

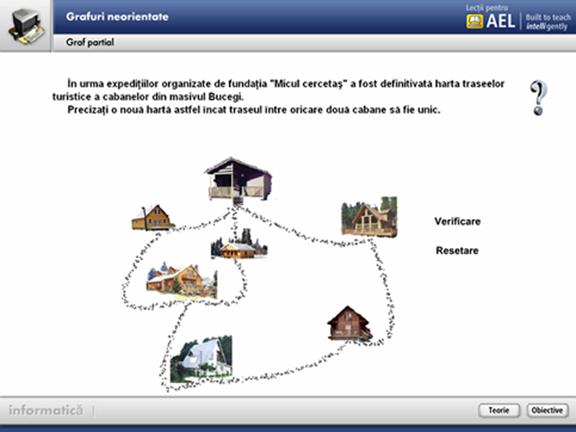
In continuare se prezinta partea teoretica a notiunii de graf partial. Elevul poate interactiona cu aplicatia folosind butoanele prezente in partea de sus a ecranului, stabilindu-se un ritm propriu de intelegre.

5.5 Subgraf

Este un obiect interactiv de tip "joc", care-l determina pe elev sa caute, sa investigheze si sa descopere un subgraf.

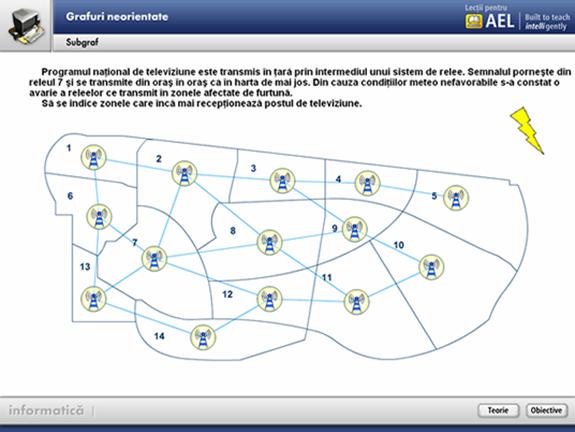
Acesta este o prezentare animata care , obsevata cu atentie , in ritmul de intelegere al elevului, pune bazele teoretice si practice ale notiunii de subgraf.

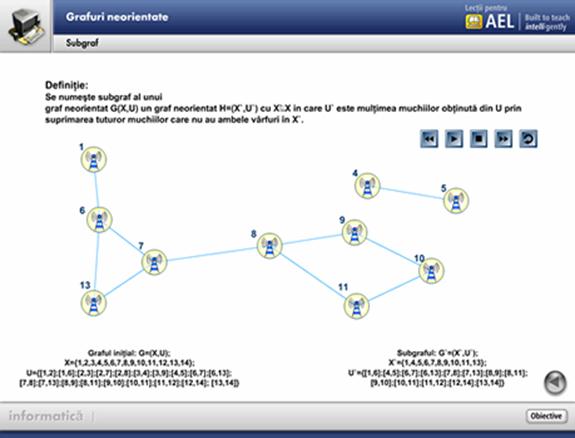
5.6 Graf Bipartit

Este un moment de tip exercitiu interactiv care pune elevul in situatia de a construi un graf bipartit.

Dupa rezolvarea exercitiului, se trece la partea teoretica a acestuia, definindu-se riguros notiunea de graf bipartit.

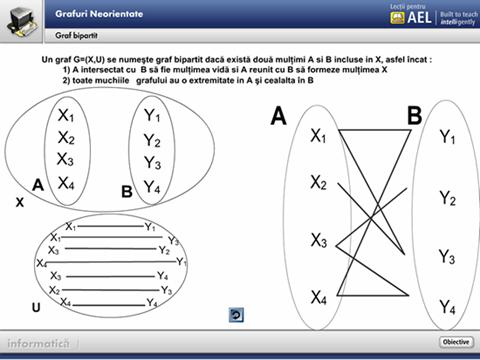
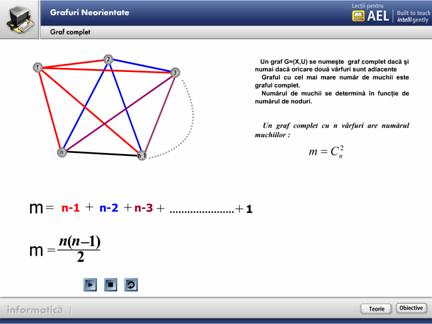
5.7 Graf complet

Prin parcurgerea acestui modul, elevul se familiarizeaza cu notiunea de graf complet.

Obiectul acesta de continut este interactiv si contine un joc. Elevul are posibilitatea sa verifice daca rezolvarea cerintei este corecta sau nu prin intermediul a doua butoane : si

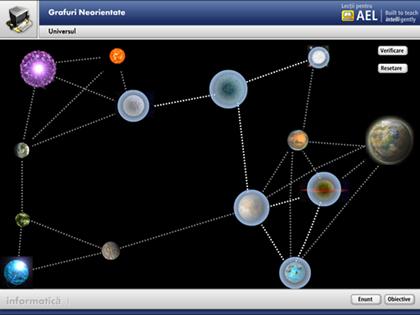
Dupa incheierea jocului se trece la o noua pagina de continut unde se explica elevului notiunea de graf complet si proprietatile acestuia.

5.8 Graf conex

Acest obiect de continut are rolul de a defini notiunea de graf conex. Este un modul interactiv care demareaza cu un joc interactiv si captivant. Jocul poate fi reluat folosind butonul sau elevul poate sa-si verifice modul de rezolvare a cerintei folosind butonul .

In final, dupa incheierea jocului, se deschide o fereastra care aminteste elevului notiunea de graf conex.

5. Tema pentru acasa

tema1

1. Reprezentati grafic toate grafurile neorientate cu 3 noduri;

2. Sa se calculeze numarul grafurilor neorientate cu n vârfuri date;

3. Sa se demonstreze ca orice graf neorientat are un numar par de vârfuri cu grad impar;

4. Determinati un graf G=(X,U) cu 5 noduri astfel încat oricare doua vârfuri a,bX, a <>b sa fie adiacente

tema2

1. Determinati numarul nodurilor corespunzatoare unui graf neorientat complet cu 36 de muchii;

2. Sa se demonstreze ca un poligon convex cu n vârfuri are 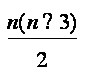diagonale;

3. Fiind dat un graf G neorientat cu n vârfuri si m muchii cu m>  , sa se demonstreze ca G nu are vârfuri izolate;

4. Graful G=(X,U) se numeste bipartit complet daca între orice vârf Xi din A si orice vârf Xk din B exista muchia [Xi,Xk]. Pentru un graf bipartit complet, pentru care multimea A are p elemente si multimea B are q elemente, sa se determine numarul total de muchii.
6. Teste de evaluare

Test1

1. Apreciati prin adevarat sau fals urmatoarea afirmatie:

Într-un graf neorientat, o muchie u este o pereche ordonata de noduri din X

Adevarat

Fals

raspuns corect : fals

2. Fiind data urmatoarea reprezentare grafica pentru un graf neorientat, atunci pentru graful G=(X,U), multimile X si U sunt:

a) X=

U=

b X=

U=

c X=

U=

d X=

U=

raspuns corect b)

Precizati care din urmatoarele notiuni se refera la grafuri neorientate:

a) muchie

b) arc

c) legatura

d) punct final

4. Apreciati cu adevarat sau fals urmatoarea afirmatie:

Doua muchii sunt incidente daca au o extremitate comuna.

Adevarat

Fals

raspuns corect : Adevarat

5. Apreciati cu adevarat sau fals urmatoarea afirmatie:

Un nod izolat are gradul 1.

Adevarat

Fals

raspuns: fals

6. Apreciati cu adevarat sau fals urmatoarea afirmatie:

Un nod terminal are gradul 1.

Adevarat

Fals

raspuns: Fals

7. Un nod este nod terminal daca:

a) nu exista muchii incidente cu el

b) este incident cu o singura muchie

c) este izolat în graful neorientat

raspuns : b

8. Un nod este nod izolat intr-un graf neorientat daca:

a) este nod terminal in graf

b) nu exista muchii incidente cu el

c) exista cel putin o muchie incidenta cu el

raspuns : b)

9. Determinati raspunsurile corecte pentru graful din figura alaturata:

a) nodul 1 are gradul 2

b) nodul 2 are gradul 4

c) nodul 3 are gradul 3

d) nodul 5 este nod terminal

e) nodul 6 este nod izolat

raspuns :a,c,d

Care este suma gradelor vârfurilor unui graf neorientat cu n vârfuri si m muchii?

a) 2*m

b) 2*(m-1)

c) 2*n

d) m

raspuns a)

Test2

1. Într-un graf neorientat G=(X,U):

Într-un graf neorientat, o muchie u este o pereche ordonata de noduri din X

a) Un graf partial al sau se obtine prin suprimarea unor vârfuri

b) Un subgraf se obtine prin suprimarea unor muchii

c) Un graf partial al sau este se obtine prin suprimarea unor muchii

d) Orice graf partial este subgraf al grafului G

raspuns corect c)

Se considera graful definit prin multimile X= si U=. Eliminând muchiile [1,2] si [3,4] se obtine:

a) Un subgraf definit prin X

b Un graf partial definit prin X si U

c) Un graf partial definit prin X si U=

d) Un subgraf definit prin X si restul muchiilor

e) Un graf partial definit prin X si restul muchiilor

raspuns corect e)

Un graf neorientat G complet cu n noduri are proprietatea

a) Contine noduri izolate

b) Are n*m muchii

c) Oricare doua noduri distincte sunt adiacente

d) Contine noduri terminale

raspuns c)

Care este numarul total al muchiilor unui graf neorientat complet cu n vârfuri?:

a) n

b) n*(n-1)/2

c) n*(n-1)

d) 2*n

raspuns b)

5. Un graf complet are 15 muchii. Câte noduri are?:

a)

b)

c)

d)

raspuns b)

6. Fie graful neorientat G=(X,U) cu X= si U=. Daca se elimina muchiile [1,2], [3,4] si [4,5] se obtine:

a) Un graf partial al grafului initial

b) Un  subgraf al grafului initial

c) Un graf complet

d) Un graf bipartit

raspuns : a,d

7. Fie graful neorientat G=(X,U) cu X= si U=. Care este numarul maxim de muchii ce se pot elimina astfel încât graful sa ramâna conex?

a) 8

b) 4

c) 5

d) 6

raspuns : c

8. Fie graful neorientat G=(X,U), X=, U=. Care este numarul minim de muchii care trebuiesc adaugate grafului pentru a deveni conex?

a) Nici una, graful este conex;

b) 3

c) 2

raspuns : c)

Fie G=(X,U) unde X este multimea nodurilor iar U este multimea muchiilor. Graful din dreapta este:

a) Un graf complet

b) Un subgraf al grafului dat

c) Un graf partial al grafului dat

d) Un graf bipartit complet

raspuns :a,b

10. Care Un graf neorientat G=(X,U) este conex daca:

a) Între oricare doua vârfuri a,b din X, a<>b, exista o muchie;

b) Între oricare doua vârfuri a,b din X, a<>b, exista lant;

c) Nu contine vârfuri izolate.

raspuns b) BIBLIOGRAFIE

N. Nedita , St Niculescu, C. Zidaroiu Matematici aplicate la tehnici de calcul.Editura didactica si pedagogica , Bucuresti 1979

C. Achinca, A. Breaz , A. Demco , M. Gradinescu, D. Grigoriu , L. Toca, C. Balanescu, R. Motruna , Bacalaureat Informatica teste grila , Editura Nedion , Bucuresti, 2003

M. Gheorghe , C . Golli , Roxana Carmen Marin , I. Oprea , Informatica , Editura Corint , Bucuresti 2003

I . Tomescu , A. Leu , Matemtica aplicata in tehnica de calcul, Editura Didactica si Pedagogica Bucuresti 1982

G. D. Mateescu , P. F. Moraru , Informatica pentru clasa a XI a , Editura Niculescu 2003

C. Ivasc , M. Pruna Bazele informaticii , Editura Petrion , Bucuresti

I. Tomescu , Grafuri si programare liniara , Editura Didactica si Pedagogica Bucuresti , 1975

T. Sorin , Tehnici de programare ., Editura Teora , Bucuresti 1994

L Toca , A. Demco , C. Opincaru , A. Sindile, Informatica - manual pentru clasa a X-a , Editura Niculescu , Bucuresti 2000