Analiza matematica

Analiza matematica

siruri de numere reale

Monotonia sirurilor

·   &nbs 555b12f p;    un sir este stationar, daca exista astfel īncāt pentru orice , , . Daca , atunci sirul se numeste sir constant.

·   &nbs 555b12f p;    un sir este strict crescator, daca exista astfel īncāt pentru orice , , .

·   &nbs 555b12f p;    un sir este strict descrescator, daca exista astfel īncāt pentru orice , , .

·   &nbs 555b12f p;    un sir este crescator, daca exista astfel īncāt pentru orice , , .

·   &nbs 555b12f p;    un sir este descrescator, daca exista astfel īncāt pentru orice , , .

·   &nbs 555b12f p;    un sir este strict monoton daca este strict crescator sau strict descrescator.

·   &nbs 555b12f p;    un sir este monoton daca este crescator sau descrescator.

Marginirea sirurilor

• un sir este marginit superior daca exista (majorant) astfel īncāt pentru orice , si īn acest caz se numeste marginea superioara a sirului .
• un sir este marginit inferior daca exista (minorant) astfel īncāt pentru orice , si īn acest caz se numeste marginea inferioara a sirului .
• un sir este marginit daca este margnit superior si este marginit inferior, adica exista astfel īncāt pentru orice , .

Observatie Un sir este marginit daca si numai daca exista astfel īncāt pentru orice sa avem .

Teorema. (Weierstrass) Orice sir monoton are limita, adica:

• daca sir crescator si nemarginit superior ;
• daca sir descrescator si nemarginit inferior ;
• daca sir monoton si marginit, atunci astfel īncāt .

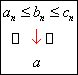
Teorema. (Criteriul clestelui) Fie , si trei siruri care satisfac conditiile:

§   &nbs 555b12f p;   &nbs 555b12f p; , (sau , unde fixat)

§   &nbs 555b12f p;   &nbs 555b12f p; .

Atunci sirul este convergent si .

Teorema. (Criteriul raportului) Fie un sir de numere reale strict pozitive si , . Daca , atunci .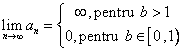

Teorema. (Stolz - Cesaro, cazul ) Fie si doua siruri cu urmatoarele proprietati:

1). , , strict crescator si nemarginit superior ().

2). sirul 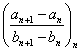are limita , .

Atunci sirul are limita si īn plus .

Consecinte

1). Fie un sir de numere reale care are limita. Atunci:

.

2). Fie un sir de numere reale pozitive care are limita. Atunci: .

3). (Criteriul lui Cauchy - d'Alembert) Fie un sir de numere reale strict pozitive. Daca sirul 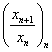are limita, atunci: .

Observatie a). Daca si , atunci ;

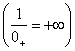
b). Daca si , atunci ; .

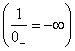Limitele sirurilor tip. siruri remarcabile.

. .

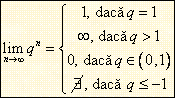. Daca , atunci .

. Fie functia polinomiala de grad cu coeficienti reali, , . Atunci: .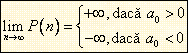

. Fie doua functii polinomiale reale, , , , , , . Atunci:

.

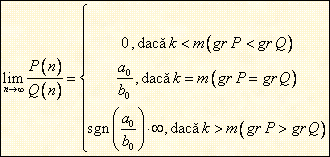. Daca este un sir convergent la 0 , , atunci:

.

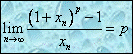
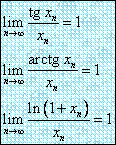. sirul cu termenul general este strict crescator si marginit: . Se

noteaza , . Exista inegalitatea . Īn plus avem:

a). Daca , atunci ;

b). Daca , , atunci ;

c). Daca , , atunci ;

d). .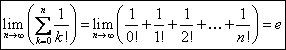

Limite de functii

1. Limita functiei polinomiale , , unde si .

·   &nbs 555b12f p;    ,

·   &nbs 555b12f p;   

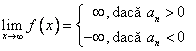
·   &nbs 555b12f p;   

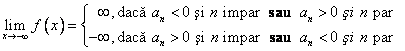
2. Limita functiei rationale , , unde , .

·   &nbs 555b12f p;    Daca , atunci .

·   &nbs 555b12f p;    Daca , atunci:

daca si obtin cazul de nedetermninare .

daca , atunci:

-   &nbs 555b12f p;   &nbs 555b12f p; daca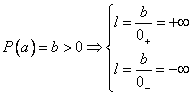

-   &nbs 555b12f p;   &nbs 555b12f p; daca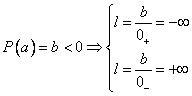

·   &nbs 555b12f p;   

3. Limita functiei radical (de ordin par) , , .

·   &nbs 555b12f p;    ,

·   &nbs 555b12f p;    .

(de ordin impar) , .

·   &nbs 555b12f p;    ,

·   &nbs 555b12f p;   

·   &nbs 555b12f p;   

4. Limita functiei exponentiale , , unde .

5. Limita functiei logaritmice , , unde .

6. Limitele functiilor trigonomtrice directe

7. Limitele functiilor trigonometrice inverse

8. Limite de functii compuse  Fie si , , punct de acumulare pentru , . Daca:

1. 
2. 
3. 

atunci .

9. Limite de puteri  Fie , , punct de acumulare pentru . Presupunem , atunci este definita.

Teorema. Daca , si daca are sens, atunci functia are limita īn si .

Cazuri exceptate (nedeterminari):

.

10. Limite remarcabile

11. Cazuri de nedeterminare , , , , , , .

Observatie. 1. Īn aceste cazuri se recomanda utilizarea limitelor remarcabile sau a regulii lui L'Hospital.

2. (Nu este caz de nedeterminare)

12. Trecerea la limita īn inegalitati

Teorema. Fie , , punct de acumulare pentru , vecinatate a lui .

Daca , , si daca au limita īn , atunci .

Corolar. Īn ipoteza de mai sus:

§   &nbs 555b12f p;   &nbs 555b12f p; Daca , , , atunci .

§   &nbs 555b12f p;   &nbs 555b12f p; Daca , , , atunci .

§   &nbs 555b12f p;   &nbs 555b12f p; Daca , , , atunci .

Teorema. (a clestelui) Daca , , punct de acumulare pentru , vecinatate a lui . Daca:

1.   &nbs 555b12f p;  , , .

2.   &nbs 555b12f p;  .

Atunci are limita īn si . Schematic avem: .

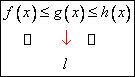Asimptote

Fie o functie. Atunci:

Observatie. O functie nu poate avea simultan asimptota orizontala si asimptota oblica la acelasi infinit.

Daca functia este rationala (adica , unde , pentru a determina asimptotele verticale cautam valorile īn care se anuleaza numitorul)

Functii continue

Fie cu . Spunem ca este continua īn daca este īndeplinita una din urmatoarele afirmatii:

1.   &nbs 555b12f p;  ;

2.   &nbs 555b12f p;  Oricare ar fi un sir din cu ;

3.   &nbs 555b12f p;  , astfel īncāt cu .

Observatie. 1. Spunem ca este continua pe daca este continua īn fiecare punct din .

2. Functiile elementare (polinomiale, rationale, radical, putere, exponentiala, logaritmicp, trigonometrice directe si inverse) sunt continue pe īntreg domeniul de definitie.

3. Daca o functie nu este continua īntr-un punct spunem ca este discontinua īn acel punct.

4. Punctul se numeste punct de discontinuitate de prima speta daca exista dar nu avem egalitatile si spunem ca este punct de discontinuitate de speta a doua daca nu este de prima speta.

Teorema. (Weierstrass) Fie o functie continua. Atunci este marginita si īsi atinge marginile.

Teorema. Daca este continua si au semne contrare, atunci astfel īncāt .

Spunem ca o functie are proprietatea lui Darboux pe intervalul , daca cu si īntre si cu , exista astfel īncāt .

Teorema. Orice functie continua pe un interval are proprietatea lui Darboux pe acel interval.

Functii derivabile

Fie , unde este un interval sau o reuniune de intervale din . Se spune ca functia are derivata īn daca exista limita (īn ). Īn acest caz aceasta limita se noteaza cu si se numeste derivata functiei īn punctul . Spunem ca functia este derivabila īn daca limita exista īn (adica exista si este finita). Īn acest caz, aceasta limita se noteaza, de asemenea, cu , adica .

Reguli de derivare

§   &nbs 555b12f p; (derivata sumei este egala cu suma derivatelor).

§   &nbs 555b12f p; (constanta iese īn afara derivarii).

§   &nbs 555b12f p; (derivata diferentei este egala cu diferenta derivatelor).

§   &nbs 555b12f p; (derivata produsului este egala cu prima functie derivata īnmultita cu a doua nederivata, plus prima functie nederivata īnmultita cu a doua derivata).

§   &nbs 555b12f p; 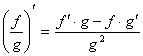(derivata cātului este egala cu derivata numaratorului īnmultita cu numitorul nederivat minus numaratorul nederivat īnmultit cu derivata numitorului, totul supra numitorul la patrat).

§   &nbs 555b12f p; (derivata unei functii compuse se obtine īnmultind derivatele functiilor care se compun īn ordinea compunerii lor).

§   &nbs 555b12f p; , unde .

Formula lui Leibniz (pentru derivatele de ordin superior) .

Proprietati ale functiilor derivabile

§   &nbs 555b12f p; Orice functie derivabila īntr-un punct este continua īn acel punct.

§   &nbs 555b12f p; Daca este o functie derivabila īn , atunci tangenta la graficul functiei īn punctul de abscisa are ecuatia: .

§   &nbs 555b12f p; Aplicatii ale derivatelor īn studiul functiilor: Fie o functie derivabila de ordinul 2 pe , unde interval. Avem:

Teorema. (Fermat) Fie o functie, unde interval real. Daca este un punct de extrem local pentru si derivabila īn , atunci .

Teorema. (Rolle) Fie si continua pe , derivabila pe si cu . Atunci astfel īncāt .

Teorema. (Lagrange) Fie si continua pe si derivabila pe . Atunci astfel īncāt .

Consecinte ale teoremei lui Lagrange

   &nbs 555b12f p;   &nbs 555b12f p;   &nbs 555b12f p;   &nbs 555b12f p;   &nbs 555b12f p;   &nbs 555b12f p;   &nbs 555b12f p;    I.   &nbs 555b12f p;  Daca , unde interval real, este derivabila si , , atunci este constanta pe .

   &nbs 555b12f p;   &nbs 555b12f p;   &nbs 555b12f p;   &nbs 555b12f p;   &nbs 555b12f p;   &nbs 555b12f p;   &nbs 555b12f p; II.   &nbs 555b12f p;  Daca sunt derivabile pe si , , atunci este constanta pe .

Teorema. (Darboux) Daca este o functie derivabila pe , atunci are proprietatea lui Darboux pe .

Teorema. (Cauchy) Fie si continue pe si derivabile pe cu , . Atunci astfel īncāt .

Teorema. (l'Hospital, cazul ) Fie doua functii cu proprietatile:

1.   &nbs 555b12f p;  derivabile pe ;

2.   &nbs 555b12f p;  ;

3.   &nbs 555b12f p;  , ;

4.   &nbs 555b12f p;  exista . Atunci exista si īn plus .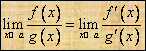

Teorema. (l'Hospital, cazul ) Fie doua functii cu proprietatile:

1.   &nbs 555b12f p;  derivabile pe ;

2.   &nbs 555b12f p;  ;

3.   &nbs 555b12f p;  , , ;

4.   &nbs 555b12f p;  exista . Atunci exista si īn plus .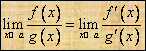

Observatie. 1. Teoremele ramān valabile si daca avem sau sau .

2. Daca este necesar si ipotezele teoremei sunt verificate putema aplica de mai multe ori regula lui l'Hospital pentru a elimina cazurile de nedeterminare.

Fie un interval real si . Spunem ca admite primitiva pe daca exista o functie astfel īncāt :

1.   este derivabila pe J;
2. ; .

Fie (J interval din ) o functie care admite primitive. Multimea tuturor primitivelor lui se numeste integrala nedefinita a functiei si se noteaza prin simbolul . Operatia de calculare a primitivelor unei functii (care admite primitive) se numeste integrare.

Reguli de integrare

1.   (integrala sumei este suma integralelor).
2.   (constanta iese īn afara integrarii).
3.   (integrala diferentei este diferenta integralelor).

Tabel cu primitivele uzuale

Observatie. , , , .

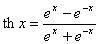Formula de integrare prin parti : .

Formula Leibniz-Newton: Fie o functie continua, iar o primitiva a lui pe . Atunci: .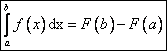

Observatie. Daca integrabila pe , atunci .

Teorema. Daca este o functie continua, atunci functia , ,

are proprietatile:

1.   este continua pe , ;
2.   este derivabila pe , , .

Aria subgraficului unei functii continue pozitive este: .