Calcul vectorial probleme

PROBLEME

Problema

Ce conditie trebuie sa indeplineasca vectorii , , , pentru a forma un triunghi?

Problema

Sa se demonstreze ca se poate construi un triunghi ale carui laturi sunt egale si paralele cu medianele unui trunghi dat ABC.

Solutie:

Notam mijloacele laturilor BC, CA, AB cu A', B', C'. Se exprima vectorii care reprezinta medianele AA', BB 424e46e ', CC' in functie de vectorii , ,

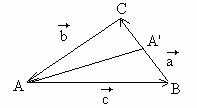
Fig.1.

Permutam circular → →→ si obtinem:

Deci, se poate construi un triunghi.

Pozitia unui punct P din spatiu poate fi determinata de vectorul , a carui origine este un punct dat O si a carui extrremitate este punctul P. Vectorul se numeste raza vectoare a punctului P in raport cu punctul O si o vom nota cu . Vom scrie, pe scurt, P().

Problema

Se cere sa se gaseasca raza vectoare a mijlocului C al segmentului AB, cunoscand punctele A(₁) si B(₂)

Solutie:

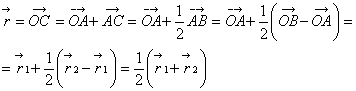
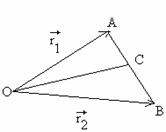
Fig.2.

Produsul vectorial

Se cunosc relatiile:

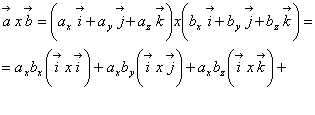
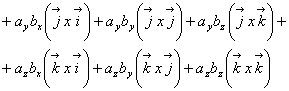
Rezulta:

2. Vectori paraleli

Problema

Sa se demonstreze ca:

Solutie:

Se aduna cele doua relatii de mai sus si demonstratia este incheiata.

Problema

Sa se gaseasca vectorul situat în planul Oyz, de lungime egala cu 10 si perpendicular pe vectorul

Solutie:

Vectorul cerut fiind în planul Oyz are b_x = 0.

Putem scrie relatiile:

Modulul

Deoarece cei doi vectori sunt perpendiculari înseamna ca produsul lor scalar este nul

Avem de rezolvat urmatorul sistem de ecuatii

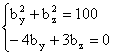
Rezulta:

Produsul mixt

Daca , atunci cei trei vectori sunt coplanari

Dublul produs vectorial

Proiectia pe axa Ox este:

Adunam si scadem în relatia de mai sus termenul a_xb_xc_x si obtinem:

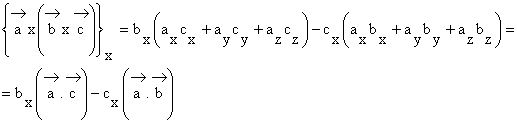
Scriem proiectiile si pe celelalte doua axe, le însumam si obtinem:

Divergenta vectorului este egala cu fluxul vectorului prin suprafata unui volum elementar care înconjoara punctul considerat raportat la unitatea de volum.

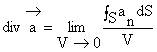
Fluxul unui vector printr-o suprafata închisa este egal cu integrala de volum din divergenta vectorului

Consideram câmpul vitezelor unui fluid real incompresibil. În acest caz volumul fluidului care trece printr-o anumita suprafata va fi întotdeauna egal cu volumul fluidului care intra, fluxul total fiind nul, de aceea

Ecuatia de mai sus se numeste în hidrodinamica ecuatia de continuitate a unui fluid incompresibil. Aceste câmpuri se numesc câmpuri fara izvoare, solenoidale sau tubulare.

Problema

Se da vectorul

si se cere sa se determine divergenta sa

Solutie:

Problema

Sa se demonstreze ca div grad φ = Δφ

Solutie:

Ecuatia lui Laplace

Δφ = 0

Problema

Se cere sa se demonstreze ca

Solutie:

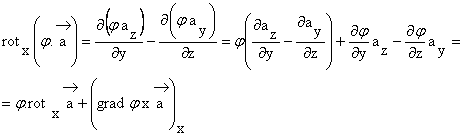
Scriem si relatiile pentru proiectiile pe celelalte doua axe si le însumam.

Probleme

Se cere sa se calculeze gradientul urmatoarelor functii:

1)

2)

Solutie:

Derivata unui vector în raport cu alt vector

Formam produsul scalar dintre vectorul

si vectorul simbolic . Obtinem:

Rezulta:

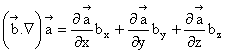
Vectori variabili

Vectorul este o functie continua de t

Pentru mai multe valori ale variabilei t extremitatea vectorului descrie o curba care se numeste hodograful vectorului .

Hodograful unui vector este locul geometric al extremitatilor vectorului care pastreaza originea.

Derivata unui vector

Viteza unui punct mobil este derivata razei sale vectoare în raport cu timpul

Directia derivatei unui vector coincide cu directia tangentei la hodograful vectorului.

Vectorul acceleratie:

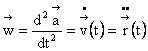
Proiectia unui vector pe o directie data. Componentele unui vector. Sistem de coordonate

direct si invers.

Alegem o directie oarecare caracterizata prin vectorul unitar . Se considera un vector .

Definitie:

Se numeste proiectia a_u a vectorului pe directia , lungimea segmentului A'B' determinat pe o dreapta oarecare paralela cu . Proiectia se ia cu semnul plus sau minus, dupa cum A'B' are acelasi sens sau sens opus cu (fig.3).

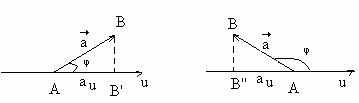
a) b)

Fig.3

a_u = a.cos(φ)

sau

a_u = a.cos(π-φ)

Proiectia vectorului pe directia poate fi considerata ca un vector _u

_u= a_u. =a.cos(φ).

Teorema:

Proiectia sumei geometrice a mai multor vectori pe o directie oarecare este egala cu suma algebrica a proiectiilor vectorilor componenti pe aceasta directie

Consideram trei vectori unitari perpendiculari între ei, orientati dupa cele trei axe ale unui sistem Oxyz de coordonate rectangulare. Acesti vectori unitari se numesc vectori fundamentali sau versori si se noteaza cu , , .

Un vector oarecare se descompune dupa vectorii , , astfel

Proiectiile a_x, a_y, a_z se numesc coordonatele rectangulare sau componentele vectorului . Aceste coordonate sunt date de expresiile:

Lungimea vectorului se determina ca diagonala unui paralelipiped rectangular, dupa teorema lui Pitagora

Directia vectorului se obtine cu ajutorul expresiilor

Avem adevarata relatia:

Exemplu din statica

Rezultanta mai multor forte care actioneaza asupra unui punct material se exprima prin suma algebrica

Proiectia rezultantei pe o directie oarecare este egala cu suma proiectiilor tuturor fortelor pe aceeasi directie

Daca vom nota proiectiile fortelor pe axele x, y, z cu X_i, Y_i, Z_i, atunci proiectiile rezultantei vor fi:

R_x = X₁+ X₂+ .+X_n; R_y = Y₁+ Y₂+ .+Y_n; R_z = Z₁+ Z₂+ .+Z_n

Marimea fortei si directia sunt date de formulele:

Daca punctul asupra caruia actioneaza un sistem de forte se afla în repaus, atunci si reciproc.

Egalitatea este echivalenta cu urmatoarele egalitati:

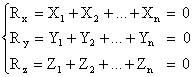
Problema

Asupra unui punct actioneaza trei forte ale caror proiectii pe axele de coordonate rectangulare sunt:

X₁ = 1, Y₁ = 2, Z₁ = 3; X₂ = -2, Y₂ = 3, Z₂ = -4; X₃ = 3, Y₃ = -4, Z₃ = 5

Se cere sa se determine marimea si directia rezultantei.

Solutie:

Produs vectorial

Problema

Se cere sa se demonstreze expresia

Solutie:

Adunam cele doua expresii de mai sus si obtinem rezultatul cerut.

Identitatea Euler - Lagrange

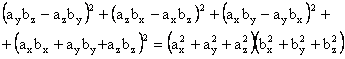
Problema

Se cere sa se calculeze expresia

Solutie:

Problema

Se cere sa se gaseasca aria paralelogramului ale carui laturi sunt vectorii:

Solutie:

Se înmultesc vectorial cei doi vectori si se tine seama de relatiile:

si de relatiile:

Rezulta:

si aria este egala cu

Problema

Se cere sa se gaseasca vectorul situat în planul yz, de lungime egala cu 10 si perpendicular cu vectorul

Solutie:

Sa notam vectorul necunoscut cu v

Avem relatiile:

Dezvoltam relatia de mai sus si obtinem:

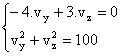
Se rezolva sistemul de mai sus si se obtine solutia

Problema

Sa se demonstreze ca ecuatia cu diferentiale totale

2zxdx+2zydy-)x²+y²)dz = 0

este complet integrabila si sa se determine solutia generala

Solutie:

Consideram câmpul vectorial

si calculam :

Liniile vectoriale ale campului sunt date de urmatorul sistem de ecuatii diferentiale

dz = 0; z = c₁

4xdx = -4ydy; xdx = -y dy

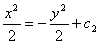
Rezulta:

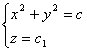
Problema:

Se cere sa se determine liniile vectoriale si suprafetele de câmp care contin curbele specificate

Curba C: xy =1; z =1

Solutie:

Formam combinatii liniare în sistemul de mai sus în vederea rezolvarii simple

(x+y)d(x+y) = (z+1)dz

(x-y)d(x-y)=(z-1)dz

Ecuatiile liniilor de câmp sunt:

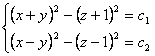
Pentru a determina suprafetele de câmp la sistemul de ecuatii de mai sus adaugam ecuatiile

xy = 1

z = 1

Înlocuim z = 1 în sistemul de mai sus si obtinem:

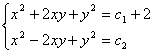
Scadem între ele ecuatiile de mai sus si obtinem:

4xy = c₁-c₂+2

Dar xy = 1 si avem

c₁-c₂+2 = 4; c₁-c₂ = 2

Suprafata de câmp este data de expresiile:

Problema:

Sa se demonstreze ca urmatorul câmp vectorial este irotational

Solutie:

Problema:

Se cere sa se demonstreze ca urmatoarele doua câmpuri vectoriale sunt solenoidale

1.

2.

Demonstratia se face calculând divergenta care trebuie sa fie egala zero.

Problema:

Se da vectorul

Sa se arate ca

Problema:

Se cere sa se gaseasca gradientul lui r, r fiind distanta punctului M fata de un punct A considerat ca origine(fig.6).

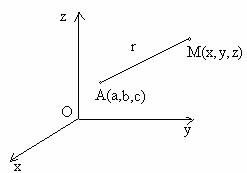
Fig.6.

Alegem ca sistem de referinta al functiei r un sistem de coordonate carteziene rectangulare cu originea într-un punct arbitrar O, diferit de punctul A.

Functia r are expresia:

Derivam functia r în raport cu x si obtinem:

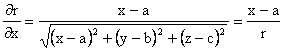
Analog obtinem:

Înmultim relatiile de mai sus cu , le adunam si obtinem:

Problema

Consideram un câmp electrostatic produs de n sarcini electrice punctiforme q₁, q₂, .,q_n. Se cere sa se determine gradientul functiei

unde r_k sunt distantele dintre punctul considerat M si punctele A_k în care sunt situate sarcinile punctiforme.

Solutie:

Folosim formulele de mai sus si obtinem:

Problema

Se cere sa se calculeze gradientul urmatorului camp scalar

si sa se determine punctele in care acesta este perpendicular pe axa Ox.

Solutie:

Sfera:

Problema

Se cere sa se determine gradientul razei vectoare

Solutie:

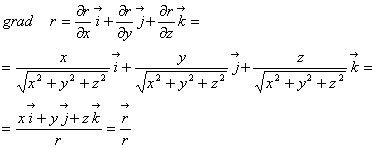
Problema

Se cere sa se determine

Solutie:

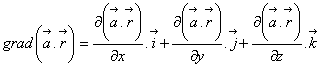
Dar, expresia produsului scalar al celor doi vectori este:

Determinam componentele vectorului gradient

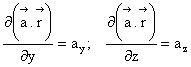
Înmultim relatiile de mai sus cu , le adunam si obtinem:

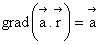
Problema

Se cere sa se determine grad r².

Solutie:

Dar,

Linii de câmp

Se cere sa se determine liniile de câmp ale câmpului vectorial definit de vectorii:

1.

Solutie:

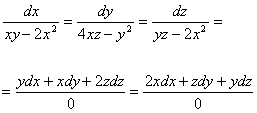
Rezulta:

2.

Solutie:

3.

Solutie: