SERII DE PUTERI REMARCABILE (UZUALE)

Seminar 3 - A.M.

SERII DE PUTERI REMARCABILE (UZUALE

TABEL 1

TABEL 2

OBSERVATII

notatii folosite

- f(x) = functia reala considerate;

- D_f = domeniul maxim de definitie, corespunzator functiei reale date f(x) ;

- S_P dezvoltarea in serie de puteri ale lui x), pentru functia reala data f(x);

- R_C = raza de convergenta pentru seria de puteri S_P;

- M_C = multimea de converganta a seriei de puteri S_P;

- M_D = multimea de divergenta aseriei de puteri S_P ;

raza de convergenta

- R_C se determina cu una din formulele F₁ sau F₂

(F₁) R_C =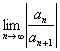

sau

(F₂) R_C =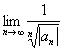

Tabel 1, Tabel 2

- seriile de puteri din aceste tabele sunt dezvoltari in serie Taylor ale

functiilor date in jurul punctului x₀ = 0 (adica in jurul originii);

4) Seria Taylor : forma generala

(S.T.) f(x) = =

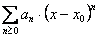
si care se numeste dezvoltarea in serie Taylor pentru functia reala data f(x) in

jurul punctului D_f , unde

- se numesc coeficientii seriei Taylor determinate in

punctul

5) Seria McLaurin :

este seria Taylor dar pentru D_f (seria Taylor in origine) si are

forma generala:

(S.T₀.) f(x) = = ,

unde

- se numesc coeficientii seriei Taylor determinate in

punctul (adica in origine)

6) Multimile de convergenta si divergenta ale seriei determinate :

- etape:

Pas1 : se determina a_n si punctul x₀ in jurul caruia se face dezvoltarea in S_P

Pas2 : se determina R_C , folosind F₁ sau F₂

Pas3 : se impun urmatoarele conditii pentru convergenta (C.C.) si

divergenta (C.D.) astfel

1) daca atunci:

(C.C.): < R_C

si

(C.D.): < R_C

sau

2) daca atunci:

(C.C.): < R_C

si

(C.D.): < R_C

Pas4 : se studiaza C / D in

1) = R_C R_C (daca )

sau

2) R_C (daca )

Pas5 : se determina M_C si M_D astfel

M_C =

si

M_D =

cu urmatoarele observatii (pentru verificare)

M_C = D_f / M_D

si M_C M_D = D_f

M_D = D_f / M_C

alte observatii

1) daca R_C = 0 , atunci M_C = si M_D = D_f /

2) daca R_C = , atunci M_C = D_f si M_D =