SERII NUMERICE IN R

SERII NUMERICE IN R

Fie sirul , un sir de numere reale. Atunci definim expresia:

(F₁) S = = =

sau

(F₂) S =

sau

(F₃) S = , unde ,

iar S se numeste serie sau suma infinita .

Pentru seria S de forma (F₁) - (F₃), termenul se numeste termenul general al seriei S si avem ca:

( termenul general al seriei S )

Pentru seria S de forma (F₁) - (F₃), definim sirul care se numeste sirul sumelor partiale al seriei S, unde:

(1) pentru S = si

(2) pentru S = si

(3) pentru S = si , unde .

Termenul reprezinta termenul general al sirului sumelor partiale si este o

suma finita de termeni, unde:

( termenul general al sirului sumelor partiale )

Natura sau tipul unei serii numerice S 2 cazuri:

(C₁) seria S este convergenta S

(C₂) seria S este divergenta S

Astfel, se impun 2 tipuri de aplicatii ( probleme ):

Tip I : Sa se studieze natura seriei numerice S date si in caz de convergenta , sa se determine

suma seriei S date;

Tip II : Sa se studieze natura seriei numerice S date, folosind criteriile de convergenta uzuale

( indicate in enunt sau nu ).

Pentru a rezolva Tip I si Tip II vom utiliza:

a)      stabilirea C / D cu definitia ( pentru Tip I );

b)      S.R. = seriile numerice remarcabile ( pentru Tip II );

c)      CRT. = criteriile de convergenta uzuale ( pentru Tip II ).

Tip I (de probleme - etape de rezolvare ).

Ip: fie data seria numerica S

C: a) sa se determine natura seriei numerice date S ( adica C / D );

b) sa se determine suma seriei numerice date S ( doar in cazul in care seria S este C ) .

D: Rezolvare ( etape ):

Pas 1 : determinam t.g.S determinam

Pas 2 : aplicam CRT.1

Pas 3 : ( daca CRT.1 )

▪ formam sirul sumelor partiale ;

▪ determinam t.g.s. determinam ;

▪ calculam

Pas 4 : ( raspuns cerinte problema Tip I )

calculam urmatoarele 2 cazuri:

▪ daca ( limita finita ) 1) S = C ( adica seria numerica data S este convergenta )

2) suma S =

▪ daca = sau nu S = D (adica seria data S este divergenta )

Tip II ( de probleme - etape de rezolvare ).

Ip: fie data seria numerica S

C: sa se determine natura seriei numerice date S ( adica C / D );

D: Rezolvare ( etape ):

Pas 1 : determinam t.g.S determinam

Pas 2 : aplicam CRT.1

Pas 3 : ( daca CRT.1 )

Aplicam S.R. ( seriile numerice remarcabile ) sau CRT.2-8 ( criteriile de convergenta uzuale )

pentru a determina natura seriei numerice date S .

Pas 4 : ( raspuns cerinta problema Tip II )

Conform rezultatului de la Pas3 stabilim in final daca seria numerica data S este C / D.

SERII REMARCABILE S.R.

A. SERIA GEOMETRICA S_g

B. SERIA ARMONICA GENERALIZATA ( RIEMANN ) S_a

Criteriile de convergenta se aplica astfel:

1. pentru serii numerice cu termeni oarecare CRT.1
2. pentru serii numerice cu termeni pozitivi ( strict pozitivi ) CRT.2 CRT.8
3. pentru serii numerice alternate CRT.9

CRITERII DE CONVERGENTA

CRT.1 ( Criteriul necesar dar nu suficient de convergenta )

▪ fie seria numerica:

S =

▪ calculam limita:

▪ atunci:

1) daca ? - studiem natura seriei numerice date S ( C / D ) cu

alte CRT. de convergenta

daca () , sau nu seria numerica data S este D

CRT.2 ( Criteriul comparatiei : I , II , III )

I.

▪ fie seriile numerice:

A =

B = astfel incat ,

, >0 ,

▪ atunci:

1) daca seria numerica B este C seria A este C

2) daca seria numerica A este D seria B este D

II. ( criteriul rapoartelor inegale al lui Kummer )

▪ fie seriile numerice:

A =

B = astfel incat ,

, >0 ,

▪ atunci:

1) daca seria numerica B este C seria A este C

2) daca seria numerica A este D seria B este D

III. ( criteriul raportului la limita )

▪ fie seriile numerice:

A =

B = calculam ,

, >0 ,

▪ atunci:

1) daca seriile numerice A si B au aceeasi natura ( ambele C sau ambele D )

2) daca si seria numerica B este C seria numerica A este C

3) daca si seria numerica B este D seria numerica A este D

Observatii:

O1. frecvent utilizat in calcule ( aplicatii serii numerice ) este CRT.2 ( III )

O2. in rezolvari se vor utiliza seriile remarcabile astfel:

▪ pentru C seriile remarcabile convergente :

S_g cu ratia

sau

S_a cu

▪ pentru D seriile remarcabile divergente :

S_g cu ratia

sau

S_a cu

CRT.3 ( Criteriul condensarii al lui Cauchy )

▪ fie seria numerica:

A =

formam seria numerica condensata A ( ):

>0 , ,

A ( ) =

( in seria numerica data A , facem : )

▪ atunci:

1) daca seria numerica condensata A ( ) este C seria numerica A este C

2) daca seria numerica condensata A ( ) este D seria numerica A este D

CRT.4 ( Criteriul radacinii al lui Cauchy )

▪ fie seria numerica:

A =

calculam limita :

>0 ,

▪ atunci:

1) daca seria numerica A este C

daca seria numerica A este D

daca ? ( aplicam un alt criteriu pentru a stabili natura seriei numerice A )

CRT.5 ( Criteriul raportului al lui D'Alembert )

▪ fie seria numerica:

A =

calculam limita :

>0 ,

▪ atunci:

1) daca seria numerica A este C

daca seria numerica A este D

daca ? ( aplicam un alt criteriu pentru a stabili natura seriei numerice A )

CRT.5 ( Criteriul lui Raabe - Duhamel )

▪ fie seria numerica:

A =

calculam limita :

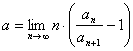>0 , sau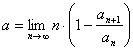

▪ atunci:

1) daca seria numerica A este D

daca seria numerica A este C

daca ? ( aplicam un alt criteriu pentru a stabili natura seriei numerice A )

CRT.7 ( Criteriul logaritmic )

▪ fie seria numerica:

A =

calculam limita :

>0 ,

▪ atunci:

1) daca seria numerica A este D

daca seria numerica A este C

daca ? ( aplicam un alt criteriu pentru a stabili natura seriei numerice A )

Observatie:

▪ pentru criteriile CRT. 4 , 5 , 6 , 7 avem urmatoarea corespondenta :

CRT.4 ( radical ) CRT.5 ( raport )

CRT.6 ( R - D ) CRT.7 ( logaritm )

CRT.8 ( Criteriul integral )

▪ fie seria numerica:

A =

determinam functia astfel:

>0 , , unde

▪ calculam :

‌‌‌|

▪ atunci:

1) daca ( limita finita ) seria numerica A este C

2) daca sau nu seria numerica A este D

SERII NUMERICE ALTERNATE

▪ forma generala:

(F₁) S = , ,

sau

(F₂) S = , >0 ,

CRT.9 ( Criteriul de convergenta pentru serii alternate - criteriul lui Leibnitz )

▪ fie seria numerica:

S = , >0 ,

▪ atunci daca sirul:

este si seria numerica S este C

Exemplu Seria armonica alternata

S = , unde S este C si are suma S =