ACTIONARI ELECTRICE

Pt. MS cu poli aparenti

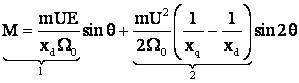
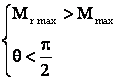
"3" mai rigida decât "1"

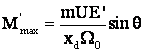
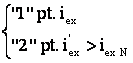
Regimuri de functionare ale MS

Din: 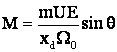   c.m. artificiale, prin:

modif. tens. de alimentare;

modif. t.e.m. E, din a i_ex (respectiv y_ex

modif. frecventei tens. alimentare.

Modific. lui E modificarea regimului de functionare.

Regimul de funct. a MS, la i_ex variabil si M art.

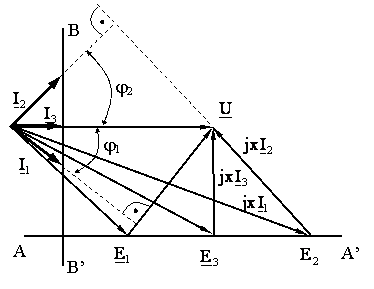Se aproximeaza .

pt.

pt.

din

din

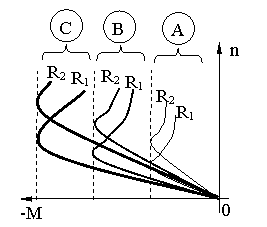
"2" I = f (i_ex curba în "v"

"1" cosj =f (i_ex

Regimuri de frânare a MS

La fel: - fr. prin c.i.

- prin alimentarea statorului cu c.c.

prin frânare dimanica.

^o - fr. prin c.i. cala MAS

putin folosita socuri de curent si M_f 0, deci nu se poate realiza o frânare;

masina trece cu funct. în asincron.

^o - fr. prin alimentarea statorului cu c.c.

ca la MAS se realizeaza;

M_f de asemenea de valoare redusa.

^o - fr. dinamica

se decupleaza statorul (rot) de la retea si cuplarea pe o rezistenta de frânare, exc. ramânând cuplata;

sau M_f cu n (pt. excit. proprie nu separata

l_f

M_f cu cresterea i_ex

M_f cu lui R_f c.m. este mai moale

rigiditate c.m. cu lui i_ex

CINEMATICA S.A.E.

Notiuni introductive.

problemele care se pun la act. el. a oricarei ML sunt multiple, si ele se refera la:

Rezolvarea acestei probleme implica cunoasterea regimurilor de funct. atât ale ML cât si a MEA.

D.p.d.v. al SAE. orice ML trebuie sa fie definita prin c.m. si prin regimul sau static de funct.

- c.m. a ML

- prin regim de funct. al ML .

Cunoasterea c.m. si a Reg. de functionare grafic de sarcina.

Pt. verificarea puterii motorului trebuie cunoscuta si variatia lui M_rt în proc. tranzitorii (pornire, oprire, reversare de sens) a SAE, sau ori de câte ori se trece de la un regim stabilizat la altul.

În proc. tranzitorii cunoasterea evolutiei lui M_rt a, v, grafice pe un ciclu complet

Din a(t), v(t) alegerea puterii mot. el. act. pt. un ciclu complet de funct.

Cinematica A.E. se ocupa cu studiul graficelor de v si a ale SAE.

Dinamica AE se ocupa de interdependenta functionala din M_motor si M_rs si M_rd ale SAE.

DETERMINAREA ELEMENTELOR GRAFICELOR DE VARIAŢIE A VITEZEI, ACCELERAŢIEI, FORŢELOR REZISTENTE sI PUTERII PT. UN CICLU DE FUNCŢIONARE

Det. corecta a puterii MEA cunoasterea graficului de sarcina si a reg. de functionare.

dar si a fortelor rezistente dinamice ce apar în reg. tranzitorii:

, iar - ac. liniara imprimata "m"

"m" - masa totala a organelor mobile

Perioada de pornire

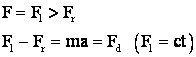
prin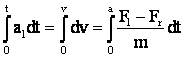

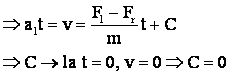
deci:    .

Pt.

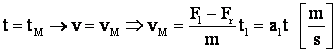
v liniar, daca F = ct., de la 0 la v_M

Dar: P = F v    sau

deci:    j de la 0 pt. t = 0 la P pt. t = t

adica   

sau daca

sau .

Perioada de regim permanent

Daca .

Asadar F = F, deci F = F_r = ct., iar P = F v_M si se mentine const.

Perioada de oprire

F < F_r cu F = ct., iar

dar F - F_r < 0, la fel a < 0 .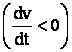

Prin integrare

Se considera conventional ca origine a timpului, sfârsitul perioadei de oprire "T ", deci v de la v_M la 0 când t variaza de la t = - t la 0 la t = 0, v = 0 C = 0.

Deci    .

Viteza variaza liniar de la v_M (la începutul lui t

sau

.

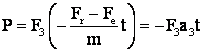Pt. t =0 si P = 0, iar pt. t = -t puterea are valoarea maxima

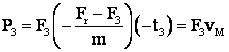
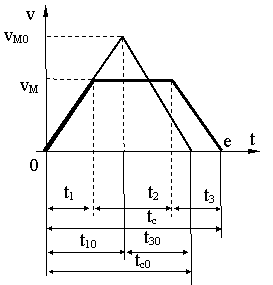
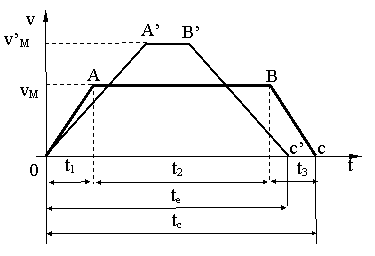
Vom considera un caz concret.

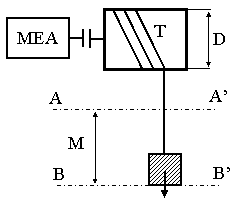
pt. un asemenea sistem graficul de variatie al vitezei este ca cel de mai sus

Se cunosc: H, t_c, G, v_M, a . Se pune problema de a determina restul elementelor necesare definitivarii graficului de viteza si acceleratie. Adica: t , t , h , h , h , t si a

Din s = vt , de asemenea

, dar

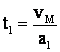, deci 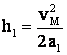. Apoi din relatia lui

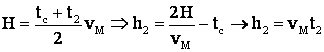(adica suprafata abcd)

Din sau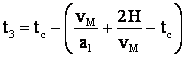

adica 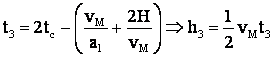   (D cd)

Apoi din 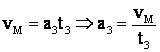q.e.d.

GENERALIZAREA METODEI DE TRASARE A GRAFICELOR DE VITEZĂ

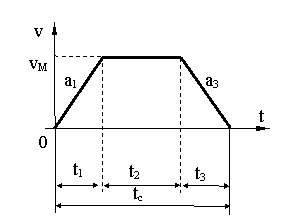t = t , IAR

t_c = t + 2t,

a = a si

v_M = a t

t necunoscut si t at_c

v_M = a at_c

Dar , dar

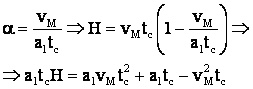
Deci   

din 3 elem. ale graficului de viteza, rezulta toate celelalte elem. nec. pt. trasarea graficului de viteza.

Deci:

a.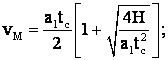

b.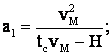

c.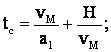

d.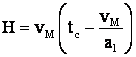

si de asemenea

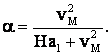
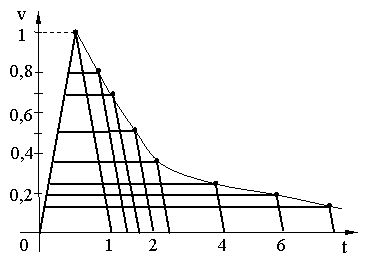
Vom considera graficul de viteza generala (oarecare)

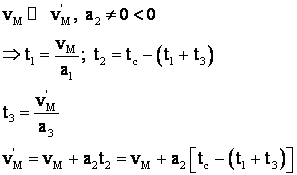
Deci

.

Înlocuind în ac. relatie valorile t si v'_M

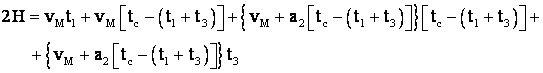
Ţinând seama de t , t functie de viteze si acceleratii

din care pt. ec. de mai sus

celelalte grafice: a, F, P.....

FORME PARTICULARE ALE GRAFICELOR DE VITEZĂ

Pt. deducerea elementelor graficelor de viteza pe lânga a 3 elem. (la trapez isoscel) se impun conditii suplimentare.

Grafice de viteza cu ciclu de functionare redus în vederea cresterii productivitatii ML

Din graficul trapezului isoscel se stie:

.

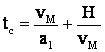H se mentine si la fel a t_c = f(v_M

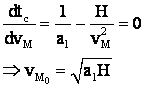
deci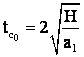   

t = 0, iar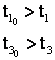

cu mentiunea .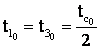

Din

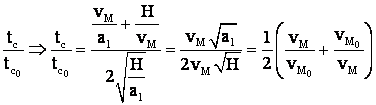
sau , luând drept. referinta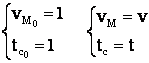

tinând seama ca:

si

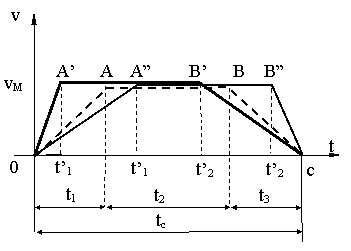
GRAFICE DE VITEZĂ OPTIME d.p.d.v. AL ÎNCĂLZIRII M.E.A.

H acelasi aceiasi v_M, dar cu t_p, t , adica cu a a , dar t_c = ct. sa se impuna si a , a

P adoptat f(q^o) mEA

grafic de viteza q minim pt "t_c P_min

a , a pt. MEA

pt. un t_c

q^o pt. MEA este ~ cu F_e (M_e

si

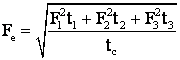
unde: , iar .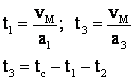

Notez:

adica: 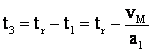si .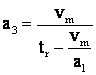

F_e devine:

din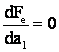 F_e încalzire minima

pt. încalzire minima

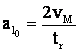
cu .

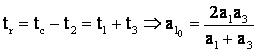În mod analog: considerând variabila

,

.

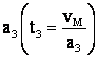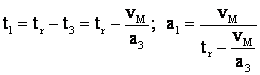Deci F_e devine:

din

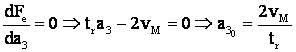
încalzire minima grafic de viteza trapez isoscel

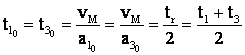
Dar: H = ct.

dar la si deci t_c

H = suprafata OA'B'C = .....

Din conditia trapez isoscel

Dar

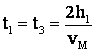
si 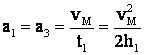din F_e

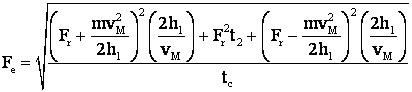
Din 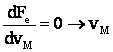pt. extrem

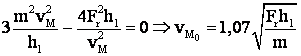
sau (pt. triunghi isoscel) .

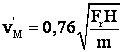GRAFICE DE VITEZĂ SPECIALE ÎN VEDEREA ATENUĂRII EFECTELOR DATORATE SMUNCITURILOR

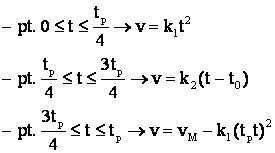
k , k constante din conditii impuse grafic. de viteza

t - abscisa lui cu axa timpului

v' si v" respectiv acceleratii, iar punctele de racordare sa fie egale, adica:

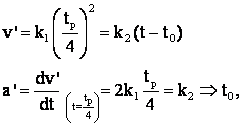adica

.

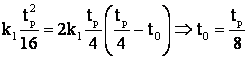Ţinând seama de coordonatele punctului A

.

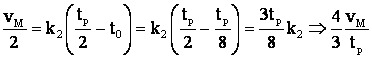Din expr. lui .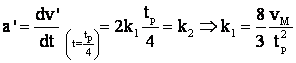

stiind k , k v' si v", anume:

.

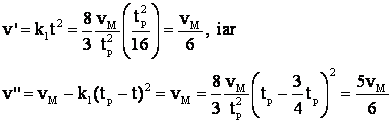Deci graficul de viteza este perfect determinat.

Pt. alte

pe intervalul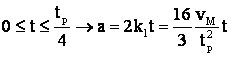

pe intervalul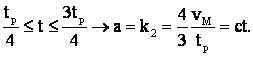

pe intervalul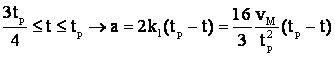

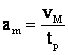- este acc. media pentru un grafic de viteza cu variatie liniara a lui v la pornire (trapez)

la si "a" discontinuitati, efectul smunciturii mult atenuat dar totusi

Din acest caz se impune: .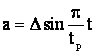

Din conditia ca acceleratia medie = ct.

.

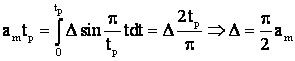Deci: 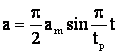   pt. viteza (în acelasi interval de timp)

.

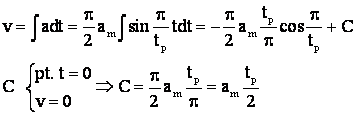Deci:    .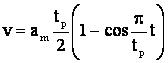

efectul smunciturii este complet înlaturat.

DINAMICA ACŢIONĂRILOR ELECTRICE

Interdependenta functionarii între MEA si ML (în regim dinamic) ecuatia echilibrului mecanic.

ecuatia fundamentala a miscarii

ECUAŢIA FUNDAMENTALĂ A MIsCĂRII

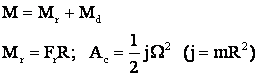
din

(ML cuplat direct cu MEA)

sau:    .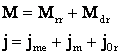

DIFERITE FORME ALE EC. FUNDAM. A MIsC.

(R - raza fictiva de rotatie, raza de giratie)

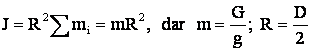
adica: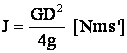   

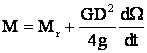
cu: 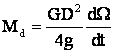   , sau în loc de W [rot/s] convine n în [rot/min].

Dar:    , adica:

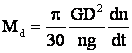
adica: 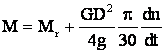   sau 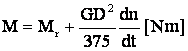fata de .

în depl. liniara v = wR

, ec. .

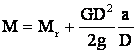ECUAŢIA FUNDAMENTALĂ A MIsCĂRII ÎN MĂRIMI RELATIVE

Din:

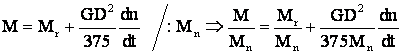
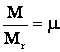- cuplul relativ dezvoltat de motor pe arborele sau

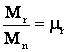- cuplul relativ static rezistent

Din: 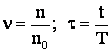   din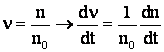

din

deci: 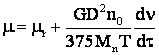   cu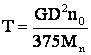

.

Gr.l act. el. cu MAS

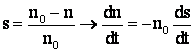si din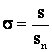

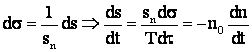
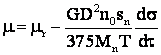, dar

.

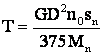
RAPORTAREA CUPLURILOR REZISTENTE STATICE sI A MOMENTELOR DE INERŢIE LE VITEZA ARBORELUI M.E.A.

E.F.M.

sau 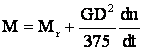, numai la cupl. directa

cuplare indirecta raportare M_r , M_d

Raportarea cuplurilor rezistente statice la viteza arborelui motor

M_r W_r ML

M_rr - cuplu raportat la W a MEA

M_rr - cuplu fictiv

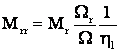, dar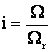

.

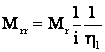Când energ. se transmite de la ML MEA si nu de la MEA ML

de regula .

Asadar: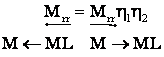   

Raportarea momentelor de inertie (volant) la viteza arborelui motor

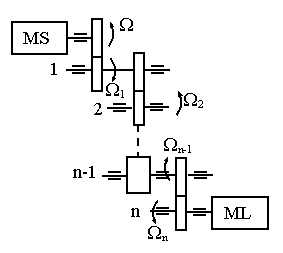
"n-1" arbori

Pt. un arbore "q" W_q, J_q

În "dt" "q" primite de la MEA lucrul mecanic "dA'_q

De asemenea:

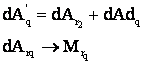
, se noteaza randanebtul transmisiei de la MEA la orborele "q" sau în intervalul dt

.

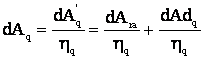Pt. toti arborii S.A.E furnizat de motor, în acelasi dt

.

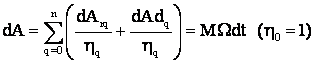La fel:

si

.

Asadar:

.

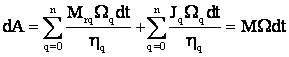Notam:

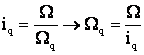si .

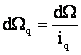Asadar:

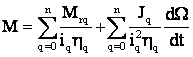, deci:

.

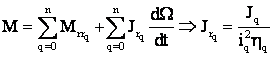Deci momentul de inertie:

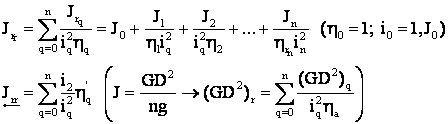
Reducerea miscarii de translatie la miscarea de rotatie si invers

cuplu dinamic pt. a imprima acceleratii maselor în miscare de translatie mase fictive în misc. de rotatie cu efect identic

în translatie

în rotatie, masele fictive .

Considerându-se ca transmisia de energie se face fara pierderi

, iar pt. o translatie reala

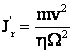h - randamentul transmisiei.

Sau din: .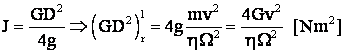

Pt. ML atât cu mase în miscare de rotatie si translatie, momentul de inertie total raportat la arborele MEA

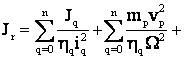sau

.

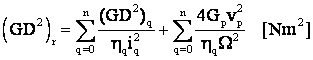Când raportarea momentelor de inertie se face la un mecanism al ML cu misc. de translatie, momentul J_i, cu W_i se pot reduce la o miscare de translatie cu viteza liniara v, având (o miscare) o masa fictiva m'

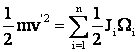sau .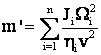

- Reducerea se face la axul oscilatorului cu misc. liniara.