BAZELE MATEMATICE ALE FIABILITATII

BAZELE MATEMATICE ALE FIABILITATII

2.1. NOTIUNI DE TEORIA PROBABILITATILOR

2.1.1.NOTIUNI FUNDAMENTALE. DEFINITII.

Fie data multimea sau populatia de elemente Γ, cu elementul generic Z

Orice fenomen sau proprietate luata in considerare fata de elementele populatiei Γ, constituie un criteriu de cercetare.

Realizarea complexului de conditii corespunzatoare criteriului de cercetare, este numita experienta sau experiment.

Orice rezultat al unui experiment poarta numele de eveniment.

Se considera un câmp de evenimente [Ω,K], unde: Ω - este evenimentul sigur si K - este multimea atasata. Daca pentru doua evenimente A si B [Ω,K], producerea unuia din ele nu depinde de producerea celuilalt, spunem ca evenimentel 919b17j e sunt independente, in caz contrar, spunem ca evenimentel 919b17j e sunt dependente.

Pentru doua evenimente A si B [Ω,K] poate avea loc o relatie de ordine, definita prin implicatiile: A B, A=B sau A B, ceea ce pune in evidenta faptul ca evenimentele prezinta grade diferite de realizare, care se cer masurate.

Masura producerii oricarui eveniment X [Ω,K], este data de functia reala P(X) pe care o numim probabilitatea evenimentului X si care satisface urmatoarele conditii, numite axiomele probabilitatii:

Consecintele acestor axiome, considerând evenimentele contrarii X si X pentru care avem si sunt:

Prin definitie, probabilitatea realizarii unui eveniment, este data de raportul dintre numarul cazurilor favorabile si numarul cazurilor posibile.

2.1.2.TEOREME FUNDAMENTALE IN TEORIA PROBABILITATILOR

2.1.2.1.Teorema probabilitatilor totale

a) Cazul evenimentelor incompatibile

Probabilitatea reuniunii unui numar finit de evenimente incompatibile este data de suma probabilitatilor acestor evenimente:

sau:

Daca evenimentele A₁,A₂,...,A_n formeaza un sistem complet de evenimente incompatibile, suma probabilitatilor lor este egala cu unitatea:

Deasemeni, suma probabilitatilor evenimentelor contrare este egala cu unitatea:

b) Cazul evenimentelor compatibile (formula lui POINCARÉ)

sau:

2.1.2.2.Teorema probabilitatilor compuse

a) Cazul evenimentelor dependente

sau:

Generalizând, prin inductie matematica se formuleaza:

sau:

b) Cazul evenimentelor independente

Probabilitatea produsului de evenimente independente este egala cu produsul probabilitatilor acestor evenimente:

sau:

2.1.2.3.Formula probabilitatilor totale

Probabilitatea unui eveniment A, care poate avea loc simultan cu unul din evenimentele (ipotezele) H₁,H₂,...,H_n, formând un sistem complet de evenimente incompatibile, este:

2.1.2.4.Teorema ipotezelor (Formula lui BAYES)

2.1.3.VARIABILE ALEATOARE

Variabila aleatoare este variabila ce poate lua o valoare oarecare dintr-un ansamblu determinat de valori si cu care este asociata o repartitie de probabilitati.

Se deosebesc doua tipuri principale de variabile: discrete si continue.

Variabila aleatoare discreta, este acea variabila aleatoare ce ia numai valori individuale, notându-se:

Marimea notata p_i=f(x_i), poarta numele de functie de probabilitate, definind distributia variabilei aleatoare.

Variabila aleatoare continua, este acea variabila aleatoare ce poate lua toate valorile unui interval finit sau infinit, notându-se:

Marimea notata (x), reprezinta densitatea de probabilitate a variabilei aleatoare continue x si are proprietatile functiei de probabilitate, adica:

sau:

Reprezentarile grafice ale distributiei variabilelor aleatoare discrete, sunt date in fig.2.1 si fig.2.2., iar ale distributiei variabilelor aleatoare continue in fig.2.3.

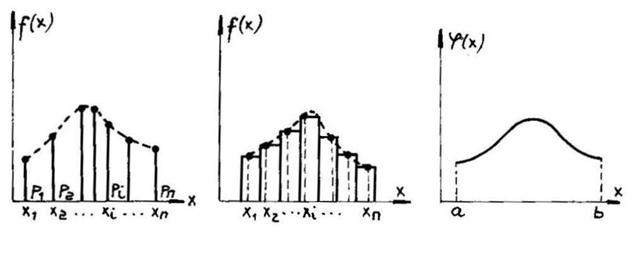
Fig.2.1. Fig.2.2. Fig.2.3.

2.1.4.FUNCTIA DE REPARTITIE A UNEI VARIABILE ALEATOARE

Functia de repartitie a unei variabile aleatoare, reprezinta functia care, pentru orice valoare x, da probabilitatea ca variabila aleatoare X sa fie inferioara sau egala cu aceasta valoare:

Aceasta functie are urmatoarele proprietati:

Pentru cazul variabilelor aleatoare continui se mai adauga si relatia:

2.2.MODELUL MATEMATIC AL FIABILITATII

Pentru construirea modelului matematic al fiabilitatii, se porneste de la indicatorii de fiabilitate (definiti la pct.1.3), pentru momentul T=t:

-z(t), rata de defectare;

-h(t)=z(t)dt, probabilitatea de aparitie a unei defectiuni in intervalul de timp (t,t+dt);

-F(t)=P(T t),probabilitatea de aparitie a unei defectiuni intre 0 si t (probabilitatea de defectare);

-R(t), probabilitatea ca defectul sa nu se produca intre 0 si t (probabilitatea de buna functionare).

Din tabelul 1.1 se scrie relatia dintre z(t) si F(t):

sau:

Integrând relatia (2.32), se obtine:

sau:

Tinând seama de conditia initiala F(0)=0, rezulta:

care este functia de repartitie a momentului defectarii.

In baza relatiilor dintre indicatorii de fiabilitate se deduc in continuare:

si:

unde, f(t) reprezinta proportia elementelor care fiind in stare de functionare la momentul 0, se defecteaza intre momentele t si t+dt.

Pe de alta parte:

sau:

In concluzie, legea de defectare, poate fi definita prin una din functiile f(t), F(t) sau z(t) legate prin relatiile:

iar functia de fiabilitate se va calcula ca R(t)=1-F(t).

Media timpului de buna functionare (mean time before failure), va fi:

Desigur, modelul matematic in functie de timp, capabil sa descrie convenabil o populatie si un fenomen evolutiv de defectare, relativ la aceasta populatie, nu poate fi caracterizat doar printr-un singur indicator de fiabilitate. Modelul matematic clasic, pentru descrierea functionarii in timp a sistemelor, il constituie procesele MARKOV, iar in particular procesele POISSON omogene, care vor fi prezentate in capitolele urmatoare.

2.3.SCHEME LOGICE DE FIABILITATE ALE SISTEMELOR COMPLEXE

In cele expuse pâna aici, in legatura cu fiabilitatea produselor, s-au avut in vedere acele produse simple, a caror defectare este ireversibila, iar momentul respectiv având semnificatia consumarii duratei de viata. In tehnica, se lucreaza insa si cu produse mult mai complexe, alcatuite uneori dintr-un numar foarte mare de elemente simple, reunite dupa anumite criterii functionale, iar ansamblul lor constituie un sistem. Daca se cunosc caracteristicile de fiabilitate ale elementelor componente, se pot stabili si caracteristicile de fiabilitate ale sistemului complex.

2.3.1.APLICAREA TEORIEI PROBABILITATILOR IN STUDIUL FIABILITATII

Pentru calculul efectiv al fiabilitatii, se utilizeaza teoremele fundamentale din teoria probabilitatilor prezentate si la punctul 2.1.2..

Considerând doar doua evenimente A si B, cele patru reguli fundamentale din teoria probabilitatilor se pot scrie:

a)Daca A si B sunt doua evenimente independente, cu probabilitatile P(A) si P(B), probabilitatea realizarii celor doua evenimente este:

b)Daca cele doua evenimente A si B se pot produce simultan (compatibile), probabilitatea realizarii lor este:

c)Daca cele doua evenimente A si B sunt incompatibile, probabilitatea realizarii lor este:

d)Daca cele doua evenimente A si B sunt complementare, intre probabilitatile lor exista relatia:

In ceea ce priveste cele doua probabilitati, de buna functionare R(t) si respectiv de defectare (F(t)), ele reprezinta doua evenimente complete si incompatibile, ceea ce face ca pentru un timp t de misiune dat sa se scrie relatia:

Pentru un sistem compus din doua elemente simple având fiabilitatile R₁ si respectiv R₂ (care se poate extinde si la "n" elemente), se vor putea scrie urmatoarele relatii de calcul al fiabilitatii:

i)probabilitatea de a avea cele doua elemente in functiune la momentul t, este:

ii)probabilitatea ca cel putin unul din cele doua elemente sa fie defecte la momentul t, este:

iii)probabilitatea ca cel putin unul din cele doua elemente sa fie in stare de functionare la momentul t, este:

iiii)probabilitatea de a avea cele doua elemente defecte la momentul t, este:

2.3.2.SISTEME CU SCHEMA LOGICA DE FIABILITATE DE TIP SERIE

Atunci când defectarea oricarui element, duce la defectarea intregului sistem (compus din n elemente simple), spunem ca din punct de vedere fiabilistic, avem o inlantuire de elemente, sau o schema logica de fiabilitate de tip serie (fig.2.4), pentru care probabilitatea de buna functionare in baza generalizarii relatiei (2.48) se scrie:

In consecinta, pentru ca sistemul sa functioneze, trebuie ca toate elementele A₁,A₂,...,A_n sa fie in stare de functionare.

In cazul particular, când ratele de defectare sunt constante (Z_i(t)=λ_i), se obtine:

unde: , este rata de defectare echivalenta a sistemului.

2.3.3.SISTEME CU SCHEMA LOGICA DE FIABILITATE DE TIP PARALEL

Sunt cazuri in care sistemul este in stare de defectare atunci când toate elementele componente sunt defecte. In consecinta, sistemul functioneaza daca un singur element functioneaza. Aceste sisteme, spunem ca au o schema logica de fiabilitate de tip paralel.

In acest caz vom considera cazul general al unui sistem format din "n" elemente (fig.2.5).

Probabilitatea ca sistemul sa fie defect este data de probabilitatea ca toate elementele sa fie defecte, ceea ce matematic

se obtine prin generalizarea relatiei (2.51):

Functia de fiabilitate va fi:

Pentru cazul particular al ratelor de defectare constante, fiabilitatea sistemului devine:

2.3.4. REDONDANTA

In cazul reproducerii schemei logice de fiabilitate a unui sistem, poate apare urmatoarea situatie: la un element (sau chiar mai multe), se constata o multiplicare, astfel incât, pentru portiunea respectiva din schema logica apare o structura de tip paralel. Spunem ca elementul respectiv prezinta o rezervare sau, schema acestuia este redondanta.

Dupa numarul elementelor redondante si functionarea acestora, deosebim urmatoarele tipuri de redondanta: redondanta simpla (cu o rezervare simpla a unui element din schema logica a sistemului), redondanta multipla (cu mai multe rezervari), redondanta secventiala

si redondanta majoritara.

In aceea ce priveste primele doua tipuri de redondanta, acestea pot fi descrise cu ajutorul notiunilor prezentate la pct. 2.3.3., fiind vorba despre scheme de tip derivatie.

Ultimele doua tipuri de redondanta le vom prezenta in continuare.

2.3.4.1.Redondanta secventiala

In acest caz elementele componente nu functioneaza simultan ca in cazul fiabilitatii de tip paralel. Elementul principal, functioneaza singur in mod normal, iar unul sau mai multe elemente sunt disponibile (in asteptare) pentru a-l inlocui când se defecteaza.

Schema logica de fiabilitate este data in fig.2.6, pentru care vom analiza functionarea in etape:

-daca elementul principal A₁, functioneaza, fiabilitatea sistemului este:

unde: R₀(t)=e^-λt, daca defectiunile urmeaza o lege de tip POISSON;

-daca A₀ se defecteaza, se pune in functiune elementul aflat in asteptare A₁, iar fiabilitatea sistemului va fi:

unde:

-daca se defecteaza si elementul A₁ aflat in asteptare, prin K₂ se pune in functiune cel de-al doilea element aflat in asteptare A₂, fiabilitatea sistemului fiind:

unde:

-daca sistemul are "n" elemente aflate in asteptare si elementul principal A₀ nu reintra in functiune, pâna la intrarea in functiune a elementului A_n de asteptare, atunci fiabilitatea unui asemenea sistem este:

Se observa ca in acest caz, chiar daca elementele de rezervare sunt identice si au rata de defectare constanta, legea (2.62) nu este exponentiala si rata de defectare a unui sistem, cu o astfel de schema logica de fiabilitate, depinde de timp.

2.3.4.2.Redondanta majoritara

Este un tip de rezervare cu cel putin trei elemente in paralel - redondanta multipla (fig.2.7). La iesirea elementelor redondante (A₁,A₂,A₃) se afla un bloc de decizie (voterul V) care permite alegerea semnalului (informatiei) eliberat de majoritatea elementelor componente (respectiv in situatia din fig.2.7, daca cel putin doua din cele trei elemente furnizeaza acelasi semnal, acest semnal va indica starea in care se afla sistemul).

Pentru a calcula fiabilitatea sistemului in acest caz, se foloseste legea binomiala. Fiabilitatea unui astfel de sistem este egala cu probabilitatea de buna functionare a doua sau trei elemente, indiferent de ordinea lor:

In cazul general, pentru "n" elemente redondante:

unde: m < n, iar R - este fiabilitatea oricaruia dintre elementele componente ale sistemului.

2.3.5.SISTEME CU SCHEMA LOGICA DE FIABILITATE DE TIP MIXT

La sistemele cu acest tip de schema, rezolvarea se realizeaza prin sectionarea schemei in subscheme cu mod de rezolvare cunoscut. Pentru exemplul din fig.2.8., fiabilitatea sistemului se va scrie:

unde:

2.3.6.SISTEME CU SCHEMA LOGICA DE FIABILITATE DE TIP OARECARE

In unele scheme logice pentru calculul fiabilitatii sistemelor, se intâlnesc legaturi intre elementele componente, care nu se pot reduce la conexiunile fundamentale serie si/sau derivatie.

Calculul fiabilitatii unui asemenea sistem se poate face apelând la formula probabilitatii totale (pct. 2.1.2.3).

Se alege un anumit element al schemei logice pentru care exista doua posibilitati (ipoteze):

- H₁elementul respectiv functioneaza fara defectiuni in intervalul de timp prescris;

- H₂elementul respectiv s-a defectat in decursul intervaluluide timp dat

Probabilitatile celor doua ipoteze, sunt complementare:

Probabilitatea functionarii fara defectiuni a sistemului, va fi:

unde: P(A_i/H₁) si P(A_i/H₂) reprezinta probabilitatile conditionate de functionare fara defectiuni ale sistemului, la functionarea fara defectiuni, respectiv la defectarea elementului A_i.

Pentru exemplul din fig.2.9, s-a aplicat setul de ipoteze (H₁,H₂) mai intâi elementului A₃ (fig.2.10 si fig.2.11), pentru care:

Daca vom nota probabilitatile de mai sus prin:

trecând relatiile (2.71) si (2.72) in domeniul timpului si inlocuindu-le in relatia (2.70), se obtine functia de fiabilitate a sistemului:

Acelasi rezultat se poate obtine si daca in loc de elementul A₃, se aplica ipotezele de mai sus celorlalte elemente (A₁,A₂,A₄,A₅).

OBSERVATIE

In cazul in care dupa aplicarea ipotezei H₁ sau H₂ elementului A_i, se obtine deasemeni o schema nereductibila (conexiuni in punte, stea sau triunghi), se mai aplica odata cele doua ipoteze unuia din elementele schemei nereductibile, calculându-se ca mai sus probabilitatea totala a acestei scheme din urma, iar cu probabilitatea determinata se utilizeaza formula (2.70) pentru determinarea probabilitatii de buna functionare a sistemului.

Astfel, se poate calcula si fiabilitatea unui sistem având schema logica de fiabilitate, cu o structura nereductibila la conexiuni serie si/sau derivatie, dintre elementele componente ale acestuia.