Circuite liniare in curent alternativ sinu 323g62d soidal

In acest subcapitol se studiaza comportarea circuitelor liniare, filiforme si cu parametri localizati, in regim electrocinetic periodic sinusoidal, numit curent alternativ sinu 323g62d soidal.

8.5.1. Marimi sinusoidale

Se stie ca o tensiune electromotoare sinusoidala, variabila in timp, poate fi produsa -in principiu- prin rotirea unei spire sau a unei bobine intr-un camp magnetic fix (fig. 8.56).

Potrivit legii inductiei electromagnetice:

sau:

(8.115)

Daca se alimenteaza cu aceasta tensiune electromotoare un circuit electric, prin circuit se stabileste un curent care trece periodic, in raport cu timpul, prin valori pozitive si valori negative. Acelasi lucru se intampla si cu celelalte marimi electrice sau magnetice: potentiale, diferente de potential, camp, flux etc.

Marimile de acest gen se exprima printr-o functie de timp . Daca marimea variabila in timp (sau in spatiu) se reproduce identic la intervale de timp egale (fig. 8.57) , ea este o marime periodica. Marimea periodica a carei variatie in timp este sinusoidala se numeste numai sinusoidala.

Intervalul de timp minim, dupa trecerea caruia valoarea instantanee a marimii periodice se repeta, in aceeasi succesiune, de un numar infinit de ori, se numeste perioada si se noteaza cu .

Rezulta, prin definitie, proprietatea:

.

Perioada se masoara in secunde.

Raportul dintre un numar intreg de perioade si timpul necesar producerii acestora se numeste frecventa :

Unitatea de masura a frecventei se numeste hertz , cu simbolul Hz.

Valoarea pe care o ia functia la un moment dat se numeste valoare instantanee si se noteaza de obicei cu litera mica. Valoarea maxima, pozitiva sau negativa, pe care o poate lua valoarea instantanee pentru o anumita valoare a variabilei, se numeste amplitudine.

Valoarea medie a unei marimi periodice, definita in intervalul de timp ,este data de relatia:

^,

iar valoarea medie patratica sau eficace, in acelasi interval de timp, se calculeaza cu relatia:

Daca valoarea medie pe o perioada a marimii periodice este nula, , marimea periodica este si alternativa (fig. 8.58).

Marimile sinusoidale variabile in timp sunt marimi periodice alternative. Ele au forma sau in care intervine ca un factor constant numit pulsatie, iar este un unghi care depinde de alegerea axelor de coordonate si se numeste faza initiala.

Unghiul , caracterizand starea functiei la momentul , se numeste faza la timpul .

Reprezentarea marimilor sinusoidale se face luand pe abscisa fie unghiul (fig. 8.59a), fie timpul (fig. 8.59b).

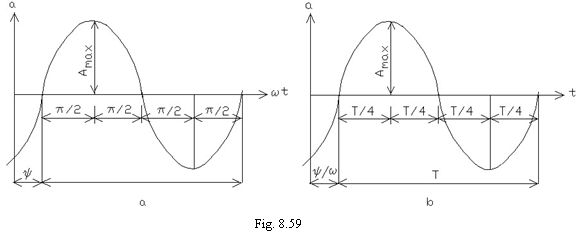
In prima reprezentare, faza la timpul este evident si deci, pentru o marime sinusoidala, perioada este:

^, (8.120)

iar frecventa:

^, (8.121)

de unde rezulta:

. (8.122)

Marimea sinusoidala se anuleaza pentru unghiul in prima reprezentare si respectiv, pentru timpul in cea de a doua reprezentare.

In retelele de curent alternativ, curentul, tensiunea si celelalte marimi electrice variaza dupa curbe asemanatoare aceleia din figura 8.58. In fapt, retelele de curent alternativ sunt retele de curent periodic. In marea majoritate a cazurilor insa, variatia acestor marimi poate fi presupusa sinusoidala, ipoteza in care se studiaza in acest subcapitol curentul alternativ.

Frecventa retelelor industriale este standardizata la 50Hz in Europa si 60Hz in S.U.A. Pentru utilizari speciale se mai intalnesc: frecvente de 25Hz si 16^2/3Hz in tractiunea electrica, 200Hz in industria lemnului si in industria miniera, 400Hz pe avioane si submarine etc. In tehnica radioului si televiziunii se utilizeaza frecvente de milioane sau miliarde de Hz. Frecventei de 50 Hz ii corespund perioada T=0,02s si pulsatia .

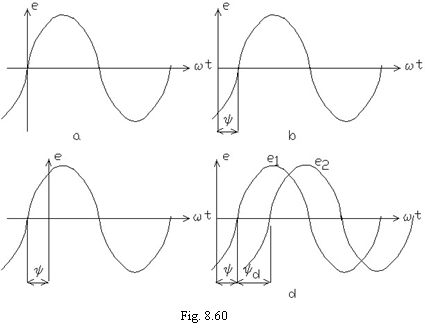
Defazajul marimilor periodice alternative sinusoidale

Tensiunea electromotoare sinusoidala avand expresia (8.115) se anuleaza, evoluand in sens crescator, in momentele date de relatia unde (fig. 8.60a). Trecand prin zero in sens crescator in momentul , corespunzator originii scarii unghiului (sau a timpului in reprezentarea in functie de timp) se spune ca marimea este in faza cu originea.

Tensiunea electromotoare , trecand prin zero in sens crescator la timpul dat de relatia (fig. 8.60b), adica la , este defazata in urma originii .

Unghiul poarta numele de faza sau defazaj fata de origine al marimii respective. Daca reprezentarea se face in functie de timp, atunci timpul este numit defazaj fata de origine.

Defazajul fata de origine poate fi si negativ. In acest caz se spune ca marimea este defazata inaintea originii (fig. 8.60c).

Marimile:

si

sunt defazate una fata de cealalta cu un unghi daca tensiunea electromotoare este defazata in urma tensiunii electromotoare , respectiv daca este defazata inaintea tensiunii electromotoare . Defazajul exprimat in timp este .

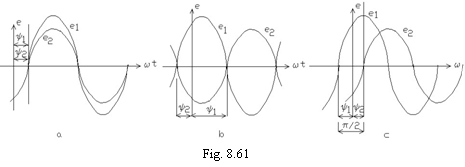
Daca cele doua tensiuni electromotoare trec simultan prin zero si prin maxim () se spune ca ele sunt in faza (fig. 8.61a). Daca in timp ce o una din ele este maxima iar cea de a doua este minima, ambele anulandu-se simultan dar in sensuri diferite, (), marimile sunt in opozitie (fig. 8.61b). In fine, daca in timp ce o marime se anuleaza, cealalta trece prin maxim sau minim, (), cele doua marimi sunt in cuadratura (fig. 8.61c).

In general, in electrotehnica nu intereseaza faza fata de o origine oarecare, deoarece aceasta depinde de alegerea originii scarii timpului. De aceea, marimile alternative sinusoidale se definesc prin amplitudinile lor si prin defazajul dintre ele, considerandu-se -in mod arbitrar- ca una din marimi, denumita origine de faza are faza fata de origine egala cu zero. Astfel, considerand in exemplul de mai sus tensiunea electromotoare ca origine de faza, cele doua tensiuni electromotoare se vor scrie: si .

Decalajul marimilor periodice alternative sinusoidale

In electrotehnica se intalnesc marimi a caror variatie sinusoidala nu se produce in timp ci in spatiu, variabila de care depinde marimea sinusoidala fiind spatiul. Unghiul in raport cu originea scarii spatiului, al functiei, se numeste decalaj fata de origine.

Decalajul intre doua functii periodice alternative sinusoidale spatiale corespunde unghiului , egal cu diferenta decalajelor fata de origine, ale celor doua functii. Toate definitiile cu privire la defazaje se aplica si decalajelor.

Marimile care difera intre ele atat in timp cat si in spatiu, se numesc defazate in timp si decalate in spatiu.

8.5.2. Efectele curentului alternativ sinusoidal

Efectul chimic. Valoarea medie a curentului si tensiunii electrice.

Conform legii electrolizei efectele chimice produse de curentul electric, depind proportional de cantitatea de sarcina electrica transportata. Pentru un curent variabil, aceasta cantitate de electricitate intr-o perioada a curentului alternativ este data de relatia:

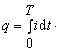
Un curent continuu, constant, care produce acelasi efect chimic, ar trebui sa aiba valoarea:

(8.123)

numita valoare medie a curentului. In mod analog se ajunge la notiunea de valoare medie a tensiunii:

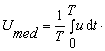(8.124)

Curentul alternativ are prin definitie valoarea medie (pe o perioada) nula si nu va produce efecte chimice. Cu atat mai mult nu va produce efecte chimice curentul alternativ sinusoidal.

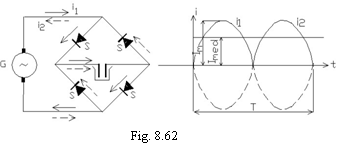
Pentru a obtine efecte chimice folosind surse de curent alternativ sinu 323g62d soidal trebuie sa procedam la redresarea acestuia. Prin baia de electroliza, datorita prezentei redresoarelor S, curentul va avea numai sensul sagetilor de pe figura 8.62. In decursul fiecarei semiperioade a curentului alternativ, baia de electroliza este strabatuta de curentii: si

Valoarea medie a curentului prin baie intr-o perioada va fi:

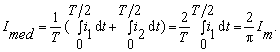(8.125)

Efectul termic. Valoarea eficace a curentului si tensiunii.

Daca un rezistor de rezistenta este alimentat la o tensiune sinusoidala , curentul in rezistor va avea intensitatea , tot sinusoidala, iar valoarea instantanee a puterii absorbita de rezistorva fi

In decursul unei perioade, circuitul absoarbe energia:

In mod practic, puterea este evaluata ca o putere medie , egala cu raportul dintre energia absorbita de circuit in intervalul de timp considerat si acel interval:

Tinandu-se seama de legea lui Ohm, se mai poate scrie:

Curentul , fiind alternativ sinusoidal, cu perioada T si avand forma:

relatia (8.126) devine:

Un curent constant, de intensitate , care sa produca in rezistorul aceeasi cantitate de caldura pe care o produce curentul sinusoidal , trebuie sa satisfaca relatia:

,

adica sa aiba valoarea:

,

numita valoare eficace (numita si efectiva) a curentului alternativ.

In mod analog se gaseste valoarea efectiva a tensiunii sinusoidale:

Punand in evidenta valorile eficace ale tensiunii si curentului, valorile instantanee ale acestora se vor scrie:

si

Valorile eficace sunt utilizate deoarece ele sunt acelea care pot fi masurate cu aparatele de masura obisnuite. Pentru a le pune in evidenta, marimile curent, tensiune, tensiune electromotoare se vor scrie in functie de valoarea eficace si nu de amplitudine, asa cum s-a procedat la scrierea expresiilor (8.130) si (8.131).

Efectul magnetic

In capitolul 5 s-a aratat ca expresia intensitatii campului magnetic H produs de solenoidul aproximat ca infinit lung are expresia (5.185'):

,

in care reprezinta numarul de spire pe unitatea de lungime a solenoidului.

Evident, daca intensitatea curentului variaza in timp dupa o lege sinusoidala, atunci intensitatea campului magnetic va avea de asemenea o variatie sinusoidala in timp:

. (8.132)

Tot dupa o lege sinusoidala vor evolua in timp inductia magnetica , fluxul fascicular etc.

Fortele electromagnetice

Un conductor de lungime , aflat in regim electrocinetic de intensitate si asezat perpendicular pe liniile unui camp magnetic uniform de inductie , este supus unei forte , perpendiculara pe conductor si pe directia campului, avand sensul dat de regula efectuarii produsului vectorial .

Un exemplu de aplicatie il constituie aparatul magnetoelectric al carui echipaj mobil este supus cuplului de forte:

Daca curentul este alternativ sinusoidal si este constant in timp, cuplul mediu la care va fi supus echipajul mobil:

este nul, deoarece . De aceea, in curent alternativ aparatul magnetoelectric nu da nici o indicatie.

Un al doilea caz, reductibil la cel de mai sus este acela al fortei electromagnetice exercitata asupra unui conductor 'parcurs' de un curent constant, de intensitate , intr-un camp de inductie magnetica periodica

Daca insa atat curentul cat si inductia sunt alternativ sinusoidale:

rezulta:

iar valoarea medie pe o perioada a fortei electromagnetice va fi:

(8.133)

Asemenea forte pot dezvolta un cuplu proportional cu valoarea lor medie asa cum se intampla la masinile asincrone.

Fortele electrodinamice

Intre doua conductoare paralele, avand curentii si se exercita forta electrodinamica (5.195):

Daca cei doi curenti sunt sinusoidali:

si

forta medie are expresia:

care conduce la:

Daca cei doi curenti sunt egali, , forta medie de atractie este proportionala cu patratul valorii eficace a curentului. Pe acest principiu se construiesc aparatele de masurat electrodinamice. Ele au doua bobine, una fixa si alta mobila alimentate in serie sau independente.

In primul caz, echipajul mobil este supus unui cuplu proportional cu valorile eficace ale curentului sau tensiunii aplicate. Aparatul masoara ca ampermetrul sau ca voltmetrul.

In cel de-al doilea caz, alimentandu-se o bobina cu o tensiune alternativa , cealalta bobina fiind 'parcursa' de curentul , produs de aceasta tensiune intr-un circuit, echipajul mobil va fi supus unui cuplu proportional cu valorile efective ale tensiunii si curentului si deci, va avea o deviatie proportionala cu puterea absorbita de circuitul considerat - aparatul va fi etalonat ca watmetru.

Forta portanta a unui electromagnet

Forta portanta a unui electromagnet de sectiune A si cu inductia B, are expresia (5.192):

In curent alternativ, ea variaza periodic cu inductia, dar ramane tot timpul pozitiva.

Inductia magnetica fiind de forma , valoarea medie a fortei portante va fi:

(8.135) .

Aparatele electromagnetice de masurat se bazeaza pe atractia unei piese de fier moale intr-un camp magnetic cu inductia , campul fiind produs de curentul din bobina fixa a aparatului. Echipajul lor mobil va avea astfel o deviatie proportionala cu patratul valorii eficace a curentului:

.

8.5.3. Calculul circuitelor in regim sinusoidal

Ca si in cazul circuitelor de curent continuu, calculul circuitelor de curent alternativ are ca obiectiv determinarea curentilor in functie de caracteristicile surselor si ale receptoarelor, curentii sinusoidali trebuind sa fie determinati prin valorile eficace si prin defazajele lor in raport cu o origine comuna a fazelor. Se utilizeaza ecuatiile (8.88) la (8.100), stabilite pentru regimul variabil oarecare, a caror aplicare prezinta insa particularitati specifice regimului sinusoidal.

Parametrii unui circuit electric de curent alternativ

Daca se aplica armaturilor unui condensator o tensiune electrica, alternativa, variabila in timp, intre aceste armaturi apare un camp electric, de asemenea variabil in timp. El va produce polarizarea dielectricului, sarcinile dipolare fiind intr-o deplasare permanenta, corespunzatoare variatiei campului respectiv. In dielectric apare un curent electric alternativ, care este un curent de deplasare (v. 4.2.1).

In consecinta, in circuitele electrice de curent alternativ pot fi inserate condensatoare ale caror armaturi sunt separate prin dielectrici.

Curentul de deplasare apare insa chiar in mediul care inconjoara elementele de circuit, intrucat intre doua elemente exista intotdeauna o diferenta de potential alternativa care produce un camp electric variabil. Prin analogie cu ceea ce se petrece intr-un condensator, este evident ca toate elementele de circuit au capacitate electrica.

Este de asemenea evident, ca orice element de circuit are inductivitate proprie sau mutuala deoarece orice portiune de circuit este inlantuita de un flux magnetic atunci cand circuitul este in regim electrocinetic. In curent alternativ, acest flux magnetic este variabil in timp si deci fiecare portiune de circuit este sediul unor tensiuni electromotoare de inductie proprie si mutuala.

In ceea ce priveste rezistenta electrica, repartizarea ei pe intregul circuit este dovedita prin degajarea de caldura care se produce chiar si in dielectricul condensatoarelor.

In practica nu se considera insa aceste fenomene fizice in toata complexitatea lor. In circuitele obisnuite se poate admite, dupa cum s-a mai aratat, ca parametrii circuitelor sunt concentrati in anumite puncte.

Astfel, in cazul unui rezistor care are o capacitate proprie precum si o inductivitate oarecare, se poate considera, atunci cand curentii de deplasare sau tensiunea electromotoare de inductie sunt nesemnificative in raport cu curentul de conductie, ca este o rezistenta pura.

La frecvente joase, inductivitatea proprie a condensatorului si curentul de conductie prin condensator sunt de neglijat fata de curentii de deplasare.

In fine, in cazul unei inductante, realizata in general sub forma unei bobine, curentii de deplasare ce apar intre spire sunt cu totul nesemnificativi fata de cei de inductie. De asemenea se poate neglija caderea de tensiune data de curentul de conductie, in raport cu tensiunea electromotoare de inductie ce apare in bobina.

Aceste aproximatii pot fi facute in toate circuitele electrice de frecventa joasa (industriala) cu exceptia liniilor lungi de transmitere a energiei electrice sau a celor de telecomunicatii. Ele au o mare importanta practica deoarece dau posibilitatea simplificarii calculelor ca urmare a neglijarii fenomenelor datorate campurilor electromagnetice variabile, luandu-se in considerare numai variatia campului electric din condensatoare si a campului electric din bobine.