ELEMENTE DE TEORIA VALURILOR

ELEMENTE DE TEORIA VALURILOR

1. ECUAŢII DE BAZĂ

Miscari cu suprafata libera produse de:

vânt;

atractia Lunii;

miscarile seismice;

deplasarea unor corpuri la suprafata apei sau în imediata ei apropiere;

miscarea frontierelor, atunci când lichidele sunt continute în spatii închise.

Ipoteze: miscare potentiala, nepermanenta a unui lichid ideal.

Integrând ecuatia lui Euler de-a lungul unei linii de curent vom avea:

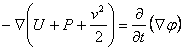(1)

Ecuatia lui Lagrange. (2)

    (3)

Suprafata apei se afla la presiune atmosferica, .

În cazul frontierelor fixe ale acvatoriului, avem:

sau

, în cazul frontierelor mobile.

2. VALURI PLANE CĂLĂTOARE, DE MICĂ AMPLITUDINE

Ipoteza suplimentara:

Amplitudinea valului mult mai mica decât lungimea sa de unda.

În aceasta situatie ecuatia lui Laplace are o solutie de forma:

, în care . . (4)

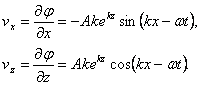    (5)

Modulul vitezei totale va fi:

În acelasi timp:

    (6)

La timpul t particula se va afla în punctul M(x,z), iar la timpul în punctul

    (7)

    (8)

Din relatiile de mai sus rezulta ca traiectoriile particulelor de lichid sunt cercuri cu centrul în punctul de coordonate si având ca raza , descrescatoare cu adâncimea.

Amplitudinea valului la suprafata este data de relatia:

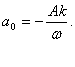    (9)

Înaltimea valului se defineste ca distanta dintre o creasta de val si un gol de val:

    (10)

În ecuatia (3) neglijam termenul în . Viteza o consideram destul de mica. Conditia la limita

ne permite introducerea termenului în .

Rezulta:

.    (11)

Viteza verticala a valului are expresia:

. (12)

Am presupus ca amplitudinea valului este mult mai mica ca lungimea de unda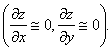

Rezulta:

(13)

si

.    (14)

Relatia (11) ne permite sa stabilim ecuatia suprafetei valului:

(15)

lungimea de unda a valului fiind:

    (16)

În Fig. 1 sunt reprezentate caracteristicile valurilor plane mica amplitudine:

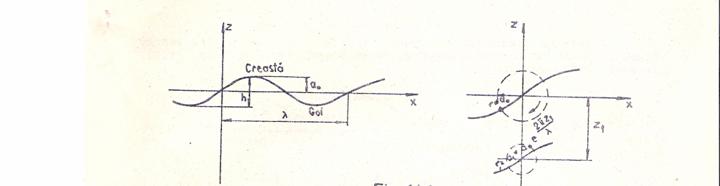
Fig. 1

reprezinta viteza unghiulara a particulei de fluid în traiectoria ei circulara.

este perioada miscarii. (17)

Din ecuatia suprafetei valului se observa ca aceasta este invariabila în timp. De-a lungul axei Ox viteza de deplasare sau de propagare a undei de val este:

    (18)

c se mai numeste si viteza aparenta. De aici provine denumirea de val calator.

Fiind vorba de o miscare potentiala, putem studia problema valurilor calatoare cautând un potential complex pentru care este o linie de curent.

Potentialul complex cautat este de forma:

(19)

Într-un sistem de axe mobil care se deplaseaza cu viteza c, fata de sistemul fix 0xz, de-a lungul axei Ox, miscarea devine permanenta (Fig. 2).

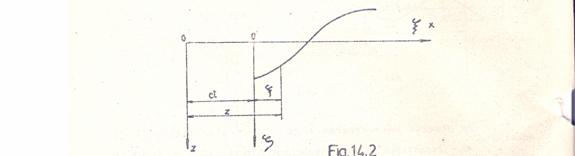
Fig. 2

Relatiile de legatura între cele doua sisteme de coordonate vor fi:

    (20)

3. GRUPURI DE VALURI

Sa consideram doua valuri calatoare, de amplitudini egale si perioade apropiate:

    (21)

Prin suprapunerea efectelor, rezulta urmatoarea suprafata de val:

(22)

Din suprapunerea celor doua valuri a rezultat un val calator cu amplitudine variabila:

    (23)

Amplitudinea variabila poate fi considerata o unda calatoare cu viteza aparenta :

sau, la limita: . (24)

Sa consideram acum cazul general în care mai multe valuri, de amplitudini diferite, lungimi de unda diferite (dar apropiate ca valoare) si defazate ( - diferitele defazari), se suprapun. Rezulta o suprafata de val de forma:

(25)

4. VALUL STAŢIONAR

Valul stationar este un caz particular de compunere a valurilor. Este vorba de compunerea a doua valuri având aceleasi caracteristici, dar mergând în sensuri contrare. Practic un astfel de val se obtine atunci când un val plan calator loveste un perete vertical, unda reflectata suprapunându-se peste unda initiala.

(26)

Valul stationar rezultat va avea suprafata de ecuatie:

(27)

5. VALURI ÎN LICHID DE ADÂNCIME FINITĂ

Conditii la limita pentru un val plan calator în situatia unei adîncimi finite:

h = adâncimea lichidului. (28)

Ecuatia lui Laplace este satisfacuta de o solutie de forma (4) în care:

(29)

Punând conditia la limita (13) - la suprafata - si (28) - la fund - obtinem sistemul:

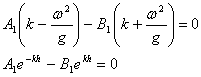    (30)

Sistemul (30) este un sistem omogen care admite solutii nenule daca :

    (31)

Deci:

    (32)

Relatiile (18) si (32) ne conduc la expresia:

    (33)

Solutia (29) va lua forma:

, (34)

iar suprafata libera va avea o expresie similara cu cea a valului plan calator de mica amplitudine:

    (35)

în care:

(36)

este amplitudinea valului si

    (37)

Procedând la fel ca în capitolul 2, obtinem traiectoriile particulelor de lichid, care de aceasta data sunt elipse.