Ventilatoare, suflante, turbocompresoare
1. CONSIDERATII ASUPRA TURBOMASINILOR 1.1. Generalitati
Turbomasinile sunt masini rotative la care comprimarea gazului sau vaporilor se obtine prin actiunea unui rotor asupra curentului permanent de gaz, modificānd presiunile si vitezele gazului.
Dupa directia de curgere a gazului sau vaporilor turbomasinile se īmpart īn doua mari grupe:
turbomasini axiale si
turbomasini centrifugale sau radiale
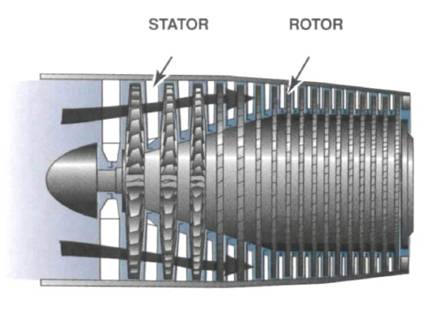
Fig. 1.1 Turbomasina de tip axial
Uneori īn clasificare se considera si o a treia grupa, denumita turbomasini "diagonele". Avānd īn vedere īnsa ca functional si constructiv aceasta grupa īmprumuta elemente atāt de la turbomasinile axiale cāt si radiale poate fi considereta o combinatie a acestora.
La turbomasinile axiale particulele de gaz sunt transportate de la intrare spre iesire pe traictorii paralele cu axa masinii, cu viteze de antrenare practic constante, iar la cele diagonale acest transport se face pe traictorii elicoidale.
La turbomasinile centrifugale, transportul particulelor de gaz se face dupa directii variabile, fiind la intrare perelele cu axa rotorului, iar la iesire radiale, deci īn rotor are loc o schimbare a directiilor cu 90°.
In figurile 1.1, 1.2 si 1.3 sunt prezentate cele trei tipuri de turbomasini.
Presiunea statica la aceste compresoare se obtine pe seama variatiei vitezei
Ventilatoare, suflante, turbocompresoare
relative si a vitezei periferice a curentului de gas ce trece prin rotor, iar presiunea dinamica prin cresterea vitezei absolute īn rotor. La iesirea din rotor se ataseaza difuzoare sau aparate directoare, care micsoreaza viteza gazului si prin aceasta transforma presiunea dinamica īn presiune statica.
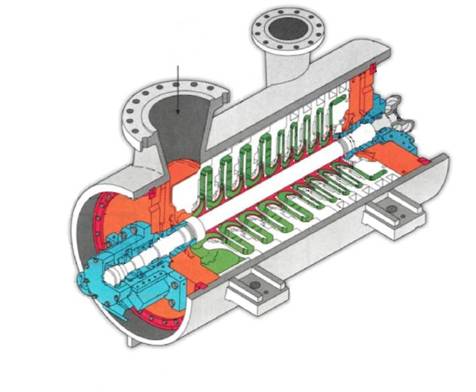
Fig. 1.2 Turbomasina de tip axial
Realizarea cresterii presiuni la turbocompresoare se face deci prin procedeul dinamic, cānd energia cinetica se transforma īn energie potentiala, spre deosebire de compresoarele volumice, la care cresterea presiunii se face prin procedeul static.
|
|
|
Fig. 1.3 Schema unei turbomasini de tip diagonal |
Din motive gazodinamice si mecanice, īntr-o singura treapta (un singur rotor) nu se poate obtine decāt o presiune limitata. Pentru obtinerea unor presiuni mai ridicate se recurge la constructia turbomasinilor īn mai multe trepte. De asemenea cu un singur turbocompresor nu se poate depasi o anumita valoare a debitului si de aceea pentru debite mai mari se cupleaza mai multe turbocompresoare īn paralel
Se mentioneaza ca turbocompresoarele nu sunt economice decāt pentru debite mai mari de 100 m3. Pentru turbomasinile frigorifice se da limita inferioara aproximativa a puterii
Ventilatoare, suflante, turbocompresoare
frigorifice pentru diversi agenti de la care utilizarea turbomasinilor devine economica.
1.2 Alegerea turbomasinilor
Pentru alegerea unui turbocompresor se cer o serie de date asupra gazului utilizat, a raportului de comprimare, a temperaturii si presiunii de aspiratie. Acesta este cazul cānd turbocompresorul functioneaza īntr-un circuit īnchis cum ar fi instalatiile frigorifice sau alte instalatii pentru vehicularea gazelor, cānd temperatura si presiunea de aspiratie ramān constante pentru un anumit regim. Pe lānga instalatiile īn circuit īnchis turbomasinile functioneaza si īn instalatii īn circuit deschis, ca de exemplu īn cazul evacuarii unor gaze din diferite spatii (la avioane, rachete, vehicule rutiere si navale) cānd presiunea si temperatura de aspiratie variaza foarte mult din cauza vitezelor si a schimbarii rapide a pozitiilor acestora. In aceste cazuri vor trebui luate masuri pentru dirijarea cāt mai judicioasa a curentului de gaz.
In cazul general pentru calculul unuei turbomasini se considera ca debitul este constant. Turatia influenteaza īn mare masura asupra dimensiunilor si constructiei masinii, deci asupra pretului. Dar turatia masinii trebuie cercetata din punct de vedere gazodinamic, al rezistentei si al conditiilor de echilibrare. Curgerea fluidelor prin masina comporta cunoasterea numarului critic Mach ca limita superioara si a numarului Reynolds ca limita inferioara.
Corelatia īntre debitul turbocompesorului , turatie si raportul de comprimare se face īn asa fel ca masina sa functioneze la un randament optim.
Ca o ilustrare a influentei turatiei asupra dimensiunilor si constructiei compresorului īn fig. 1.5 se dau marimea si numarul de rotoare pentru aceleasi coditii de functionare.
1.3. Puterea turbomasinilor
Pentru a arata functionarea unuei turbomasini, īn practica s-au stabilit anumite legaturi īntre debitul aspirat, presiunea de refulare, turatie si randament. Aceste dependente se arata grafic prin asa numitele curbe caracteristice.
Pe abscisa se trece debitul aspirat, iar īn ordonata diferenta totala de presiune Aptot, raportul de comprimare p2 tot/p1 tot sau lucrul mecanic adiabatic Had (aici s-a
considerat comprimare adiabata).
Lucrul mecanic de comprimare adiabat se determina cu expresia:
Ventilatoare, suflante, turbocompresoare
k-1
H
k-1
RT
p2
vp1y
, [J/kg]
unde:
|
=const. |
T1 - temperatura de aspiratie, [K]
k - exponentul adiabatic
R - constanta specifica a gazului, [J/kgK]
p1 - presiunea de aspiratie, [N/m2]
p2 - presiunea de refulare, [N/m2]
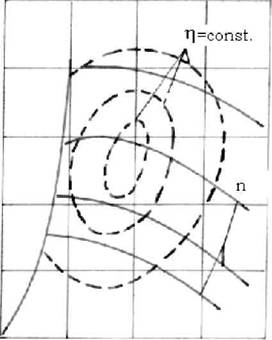 H
H
ad
[m]
piJp
Ap tot
[N/m2]
V [rn/s]
Fig. 1.4 Dependenta īntre debitul aspirat V īnaltimea de refulare Had , turatia n si
randamentul K al unei turbomasini
Pentru rapoarte mici de comprimare, pāna la 1,1, relatia (1) se poate reduce la
forma:
|
ad |
H^p2 p1 , [J/kg]
Um
unde:
U U [kg/m3] este densitatea medie a gazului
īntre intrarea si iesirea 2
din turbocompresor.
Lucrul mecanic adiabatic se defineste si īn functie de lucrul mecanic teoretic cu
ajutorul randamentului adiabatic:
Ventilatoare, suflante, turbocompresoare
Kad=HL
Ht
Presiunile px si p2 sunt considerate ca presiuni totale, deci ca sursa a presiunilor statica si dinamica:
ptot=ps+pd
Presiunea dinamica pd arata o crestere a presiunii totale datorita transformarii
energiei cinetice īn energie potentiala. Pentru viteze ale gazului mai mici decāt viteza sunetului, presiunea dinamica se determina, destul de exact, cu expresia:
pd =U-, [N/m2]
In aceste conditii puterea unui compressor este:
P = , [W]
K ad
sau:
ĪYlTJ
P = ad [kW]
unde: m este debitul masic, [kg/s].
Pentru diferente mici de presiune expresia puterii devine:
V p2-pi
, [W]
K
ad
sau:
P = p2pli [kW]
unde: V este debitul volumic la aspiratie, [m3/s]
1.4. Presiunea realizata īn turbomasini
Presiunea totala realizata īn turbomasini se compune din presiunea statica, din caderea de presiune datorita frecarilor īn canale si conducte si din energia cinetica pe care o mai poseda gazul la iesirea din compresor (difuzor).
U2
Aptot =Aps+Y, ^pfr + vd
unde:
vd este viteza de iesire din difuzor.
Ventilatoare, suflante, turbocompresoare
In foarte multe cazuri turbomasinile sunt folosite numai la transportul gazelor īntr-un sistem de conducte, ceea ce revine la a realiza o presiune Aptot numai
īnvingānd frecarile si realizānd o energie cinetica corespunzatoare unei viteze v.
cond
Deci:
Aptot = X Apfr + - vc2ond
unde:
vcond este viteza de iesire a gazului din sistemul de conducte.
Presiunea realizata īn turbomasini poate fi considerata ca fiind compusa din presiunea utila si pierderile de presiune cauzate de curgerea gazului.
Pentru a lamuri aceasta, se considera un racitor de gaz, intercalat īntr-un sistem de conducte, la care "presiunea utila" este considerata caderea de presiune īn racitor, iar pierderile datorita curgerii sunt o suma de pierderi de curgere īnainte si dupa racitor, plus energia gazului la iesirea din racitor.
Aceste pierderi de curgere pot fi exprimate printr-un randament gazodinamic, a carui expresie este:
Kh=
p tot ~ p tot
unde: p2 tot p1 tot este diferenta totala de presiune īn turbocompresor.
Produsul dintre randamentul gazodinamic K h si randamentul procesului de comprimare Kad da randamentul sistemului sau al instalatiei:
K h K
K inst ad
De multe ori turbocompresorul aspira dintr-un sistem de conducte, īn care caz, caderea de presiune datorita curgerii gazului prin sistemul de conducte este considerataca "presiune utila". Deci pierderea de presiune care este luata dupa turbocompresor, este considerata ca pierdere a instalatiei. Pierderile instalatiei includ si pierderile īn difuzor plus pierderile de energie cinetica la iesirea gazului din instalatie. Deoarece gazul iese īn atmosfera, diferenta de presiune a instalatiei, īn aceste cazuri, este diferenta īntre presiunea atmosferica pat si presiunea totala la
intrarea īn turbocompresor p1 tot .
In acest caz pentru randamentul instalatiei se obtine:
Kinst= p«t~p°'
pi tot ~ p tot
K ad
Ventilatoare, suflante, turbocompresoare
La o instalatie cu difuzor pentru randamentul hidraulic Kh se pot lua valori de 0.88y0.92.
Notānd cu Apc = p2 tot -pat, pierderile dupa turbomasina se obtine:
K h c
pi tot p at
Pierderea de presiune dupa turbomasina Apc este o suma de pierderi asa cum s-a aratat:
Apc-U vd2+U 1-K d(vr2-vd2) + U vu2
unde:
vr [m/s] este viteza meridiana la iesirea din turbocompresor;
va [m/s] este componenta periferica a vitezei
vd [m/s] este viteza de iesire din difuzor;
Kd [-] este randamentul difuzorului
v2 La ventilatoarele axiale si radiale, cu aparat de ghidare termenul U u este
foarte mic si poate fi neglijat, dar la cele axiale, fara aparat de ghidare, acest termen trebuie luat īn considerare, mai ales la īncarcari mari gazodinamice.
1.5. Utilizarea turbomasinilor
Multiplele domenii de utilizare a turbomasinilor impun o scurta prezentare a acestui subcapitol.
1.5.1 Conditionari si instalatii firgorifice
Pentru desfasurarea unor procese tehnologice sau pentru realizarea confortului īn spatiile unde oamenii īsi desfasoara activitatea este nevoie ca parametrii aerului (temperatura si umiditatea) sa fie pastrata īn limitele prescrise. In acest scop se folosesc instalatii de conditionare care pentru antrenarea aerului utilizeaza turbocompresoare, grupate īntr-o centrala.
Caldura care trebuie evacuata sau introdusa īn spatiul de conditionat este data de relatia:
Q> = V-cp-U-M, [W]
unde:
Ventilatoare, suflante, turbocompresoare
cp [J/kgk] - caldura specifica a aerului;
U [kg/m3] - densitatea aerului;
AT [grd] - diferenta de temperatura īntre intrarea si iesirea aerului din spatiul de conditionat;
V [m3/s] - debitul aspirat de turbocompresoare
De asemenea, īn industria chimica, pentru sinteza diferitelor substante, īn industria petrochimica, la conditionarea aerului, la prelucrarea si pastrarea produselor perisabile, este nevoie de folosirea frigului.
Multe procese tehnologice se intensifica sub influenta frigului, iar altele au loc numai daca se petrec la temperaturi scazute. Capacitatile frigorifice mari, cerute īn aceste sectoare impun folosirea instalatiilor frigorifice cu compresoare radiale.
Capacitatea frigorifica a compresorului radial este:
qv-V, [W]
unde:
q q0 [J/m3] - puterea frigorifica specifica volumica;
v1
q0 Aiv [J/kg] - puterea frigorifica specifica masica;
Aiv [J/kg] - variatia entalpiei agentului frigorific īn vaporizator;
v1 [m3/kg] - volumul specific la aspiratie, īn turbocompresor.
Ca agenti frigorifici se folosesc deferite fluide, care necesita adaptarea unei diversitati de tipuri constructive de compresoare radiale.
Pentru comprimarea freonului si propan-propilenei se folosesc turbocompresoare cu difuzor nepaletat si unghi de iesire a paletelor rotorului de 20.450. Cifra Mach īn functie de viteza periferica a rotorului este de 1,2. 1,4. La aceste compresoare radiale vitezele periferice curent utilizate sunt de 190 m/s pentru freoni si 275 m/s pentru propan. Tot pentru freoni se folosesc si compresoare radiale cu difuzor paletat, atingāndu-se viteze periferice de 195 m/s. Compresoarele radiale pentru freoni se construiesc īntr-o gama foarte larga cu puteri frigorifice de (0,64 ÷ 7)∙103 kW, īn functie de temperaturile de vaporizare cerute de consumator si de puterile frigorifice necesare.
Pentru comprimarea amoniacului, compresoarele radiale se construiesc īn mai multe trepte cu numere Mach de 0,7 ÷ 0,9 raportate la viteza periferica a rotorului, cu unghi de iesire a paletelor rotorului de 20 ÷ 90ŗ, cu viteze periferice pāna la 275m/s pentru rotoare din otel si de 350 m/s pentru cele din titan si difuzoare, īn general, paletate.
Ventilatoare, suflante, turbocompresoare
Constructiile actuale de compresoare radiale utilizeaza turatii de 6000 ÷ 15000 rot/min, diametrele rotoarelor variind īntre 250 si 480 mm, iar camera spirala este īn general de constructie asimetrica.
Ventilarea tunelelor
Traseele trenurilor subterane, a metrourilor, autostrazilor subterane trebuiesc ventilate, pentru a mentine īn limite acceptabile continutul de monoxid de carbon, care nu trebuie sa depaseasca 0,25% participatie volumica. In medie, se poate aprecia continutul de CO provenit de la motoarele cu explozie cca 150 cm3 de fiecare vehicul si metru de tunel. Pentru masinile grele aceasta cantitate poate ajunge pāna la 200 cm3 pe vehicul si 220 cm3 īn cazul motoarelor Diesel. Viteza de īnaintare a vehiculelor īn tunel se apreciaza la 24 km/h.
Problema ventilarii tunelelor revine īn a determina debitul de aer proaspat, dupa relatia:
V tYq c , [m 3 /s-m]
īn care:
V [m3/s∙m] - debitul de aer proaspat pentru un metru lungime de tunel;
N [-] - numarul de vehicule pe ora ce trec prin tunel;
b [%] - concentratia volumica admisibila de CO;
c [-] - coeficient ce depinde de natura motorului autovehiculului si are valoare 1,0 pentru motoare cu benzina si 1,1 pentru motoare Diesel.
Aceasta cantitate de aer proaspat este introdusa īn tunel cu ajutorul turbocompresoarelor de debit foarte mare.
Ventilarea minelor
Conditiile de lucru īn subteran cer instalatii speciale de ventilare a galeriilor si abatajelor. Vor trebui luate masuri pentru īndepartarea gazelor toxice si explosive ca si a prafului rezultat din sfarāmarea rocilor.
Pentru reīmprospatarea aerului se utilizeaza turbocompresoare de mare debit, de regula axiale, cu o presiune pāna la 600 mmH20, asigurānd un necesar de aer proaspat de 2 ÷ 5 m3/min pentru fiecare miner.
De regula aerul este aspirat din mina īn anumite puncte ale sistemului de galerii, iar īn alte puncte este introdus cu o usoara suprapresiune. Aceste instalatii de
Ventilatoare, suflante, turbocompresoare
ventilare au un regim special de exploatare si se cer conditii extrem de severe pentru siguranta.
1.5.4. Racirea motoarelor cu ardere interna
Pentru racirea motoarelor cu ardere interna se utilizeaza un curent de aer produs de un ventilator axial, de regula montat pe axul motorului. Fluxul de caldura preluat de aer este:
Oaer=D-O =D-B-Pef-Qi, [kw]
unde:
[kJ/h]- fluxul de caldura produs prin arderea combustibilului; D 0.3 [-] - coeficient ce arata cāta caldura este preluata de aer; B [kg/kWs] - consumul specific de combustibil; Pef [kW] - puterea efectiva a motorului;
Qi [kJ/kg] - puterea calorica inferioara a combustibilului.
Considerand un sistem de racire al unui motor, racit cu un racitor cu ventilator axial, caderea de presiune totala īn sistem poate fi pusa sub forma:
Aptot - 4pR U U ucul, [mmH 2 0]
2g 2g
īn care:
ApR U v 2 R-cR- pierderea de presiune in racitor; 2g
vR [m/s]- viteza aerului īn racitor;
cR [-] coeficient de curgere pentru racitor, a carui valoare este de 2 ÷ 5, iar īn cazuri speciale 10.
ApR =50 ÷ 100 mmH20, īn cazuri speciale 200 mm H2O.
Api - i n ivi2ci - pierderea de presiune datorita drumului parcurs de aerul de
i=0 2g
racire,
vi [m/s] - viteza aerului īn diferite sectiuni,
ci [-] - coeficient de curgere pentru diferite sectiuni. U v 2 - energia cinetica de iesire a aerului din racitor,
aer
2g
vvehic l1-[ - presiunea cauzata de vānt sau de īnaintarea vehiculului, 2g
Ventilatoare, suflante, turbocompresoare
[-] - coeficient ce tine seama de orificiile de racire a aerului, care este
pozitiv, doar uneori negativ.
Instalatia de racire cu ventilator axial, la vehicule de transport, consuma cca 2 ÷ 4 % din puterea efectiva a motorului, iar la autovehiculele grele acest procent se ridica la 12 %.
La motoarele de avion racirea se face prin aerul circulat de elice, care este un ventilator axial. In timpul zborului racirea este realizata si de curentul de aer produs de īnaintarea avionului. Instalatia de racire a motorului, trebuie sa fie dimensionata, pentru conditiile termice cele mai defavorabile, adica la decolare si dupa aceea īn timpul ridicarii, cānd īnaltimea este mica si viteza de zbor destul de redusa, deci actiunea de racire este scazuta.
La īnaltimi mari, ca urmare a rarefierii aerului, transferul de caldura este diminuat, deci si eficacitatea racirii este micsorata.
Din cauza ca o suprafata de racire adecvata nu poate fi utilizata din lipsa spatiului de amplasare, racirea numai prin actiunea elicei si a curentului de aer nu este suficienta si atunci s-au prevazut alte mijloace de racire prin instalatii speciale cu agenti de racire (apa, glicol, etc.).
1.5.5. Tunele aerodinamice
Pentru īncercarea profilelor aerodinamice se folosesc tunele aerodinamice cu un debit foarte mare, īn care curentul de aer este creat de suflante axiale.
Aceste tunele pot fi subsonice sau supersonice. La tunelele subsonice viteza de trecere a aerului prin sectiunea de masurare este de cca 60 m/s, diametrul duzei de cca 3 m, iar turatia suflantei de 600 rot/min, cu o putere de 600 kW, pentru motoare de curent continuu.
Viteza de trecere poate fi marita pāna la 100 m/s, īn cazul sectiunilor de masurare īnchise, cu duze avānd diametrul de 2 m si o turatie a suflantei de 600 rot/min.
In cazul tunelelor supersonice īnchise, se utilizeaza un turbocompresor axial īn mai multe trepte, care trebuie sa creeze o presiune care sa īnvinga rezistentele de frecare īn canal.
Pentru o apreciere aproximativa a acestor tunele e bine a se recurge la utilizarea relatiei īntre numarul Mach si raportul presiunilor compresorului, care de cele mai multe ori se da sub forma de diagrama.
Ventilatoare, suflante, turbocompresoare
1.5.6. Alimentarea furnalelor si otelariilor
Cantitatea mare de aer necesara pentru insuflarea īn furnale sau in cuptoarele otelariilor este livrata de suflante axiale sau radiale. Cantitatea de aer necesara pentru aceste scopuri se ridica pāna la 190000 m3/h si mai mult, cu puteri de antrenare de peste 10000 kW.
Suflanta radiala tip R 140 construita de U.C.M.Resita, pentru furnale, are un debit de 150000 m3/h la 3,5 bari si o putere de 10000 kW, la o turatie de 3000 rot/min.
Suflantele pentru furnale se calculeaza īn functie de productivitatea zilnica de fonta. In figura 1.8 se indica debitul de aer pe care trebuie sa-l asigure suflantele īn functie de productia zilnica de fonta.
Pentru otelarii debitul de aer este 2000 ÷ 2800 m3/h pentru o tona de otel. Raportul de comprimare p2/p1 la aceste suflante variaza de la 2,8 pāna la 4,0.
1.5.7. Alte utilizari 1.5.7.1. Transportul pneumatic
La transportul pneumatic, turbocompresoarele comprima aerul care este purtatorul materialelor de transport. In general se utilizeaza transportul direct si sarcina unui astfel de turbocompresor, īn acest caz, se īncadreaza īntre 250 ÷ 500 mmH2O.
Pe lānga transportul pneumatic, sub presiune, se utilizeaza si transportul pneumatic sub depresiune. La instalatiile cu depresiune sarcina este 3000 ÷ 5000 mmH2O.
Pentru calculul turbocompresorului trebuie cunoscute debitul de aer Vaer si volumul materialului de transportatVm . Facānd raportul lor rezulta:
Vm P
V
aer
unde: P 1/250 y1/1500 sau chiar mai putin, poarta numele de coeficient de amestec sau transport.
Pentru materiale foare fine valoarea lui P 1/800y1/1500 .
Ventilatoare, suflante, turbocompresoare
1.5.7.2. Supraalimentarea motoarelor cu ardere interna
Puterea unui motor cu ardere interna depinde īn primul rānd de arderea combustibulului cu o cantitate adecvata de aer. Aceasta putere creste cu presiunea aerului introdus, necesar arderii. Ca urmare, aerul este introdus cu ajutorul unor turbocompresoare. Debitul de aer necesar pentru alimentarea motorului, īn kg/s, este:
V V- - -O-U, pentru motoare īn patru timpi
aer
V V- - -O-U, pentru motoare īn doi timpi aer
unde:
V [m3] - volumul generat de cursele pistoanelor motorului;
n [rot/min] - turatia motorului;
O [-] - coeficientul volumic de alimentare;
U [kg/ m3] - densitatea aerului introdus.
Coeficientul volumic de alimentare O are valoarea 0,8÷ 0,92 pentru motoarele īn patru timpi si 1,5 ÷ 2,5 la motoarele īn doi timpi.
1.5.7.3. Turbinele cu gaz
Pentru utilizarea turbocompresoarelor este important de amintit domeniul turinelor cu gaz, care īn ultimul timp au luat o dezvoltare foarte mare datorita indicilor tehnico-economici ridicati. Din puterea totala produsa de turbine o parte este consumata de turbocompresor.
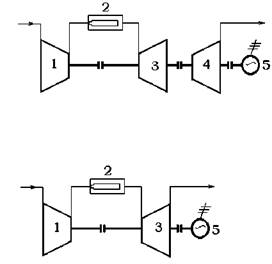 Fig.1.9 Cuplarea turbocompresoarelor cu
Fig.1.9 Cuplarea turbocompresoarelor cu
turbine cu gaz
1 - turbocompresor; 2 - camera de ardere
3 - turbina; 4 - turbina de lucru; 5 - generator
Aranjamentul turbocompresoarelor cu turbinele se practica īn special la turboreactoare, unde gazele de ardere expandeaza dintr-o turbine cuplata cu un compresor centrifugal sau axial, care trimite aerul īn camera de ardere.
Ventilatoare, suflante, turbocompresoare
2. MARIMILE CARATERISTICE ALE TURBOMASINILOR PEBAZA LEGII
SIMILITUDINII LUI NEWTON 2.1. Scopul marimilor caracteristice
O metoda de investigare folosita pentru cercetarea īn vederea īmbunatatirii performantelor actuale cu scopul de a satisface cerintele crescānde impuse de noile tehnologiii se bazeaza pe teoria similitudinii. Dupa cum se stie, teoria similitudinii permite sa se obtina o serie de masini derivate, cu acelasi randament ca al masinii model, dar cu parametri diferiti de ai modelului. Se poate afima ca randamentele a doua turbomasini vor fi egale daca sunt īndeplinite urmatoarele conditii:
similitudinea geometrica, extinsa la conditiile limita, a celor doua compresoare;
similitudinea triunghiurilor vitezelor īn sectiunile de curgere omoloage;
aceleasi valori numerice pentru criteriile de similitudine pe model si prototip īn sectiunile omoloageale acestora;
egalitatea exponentilor adiabatici ai gazelor care se comprima.
2.2. Criteriile de similitudine 2.2.1. Definitia similitudinii mecanice
Pentru ca fenomenul reprodus de model sa fie absolut identic cu fenomenul pe prototip, pe lānga similitudinea geometrica dintre model si prototip-extinsa la conditii limita si caracterizata printr-un raport de similitudine geometrica - mai trebuie sa se realizeze similitudinea tuturor marimilor fizice care intra īn structura fenomenului studiat. Aceasta īnseamna ca īn fiecare pereche de puncte omologe, la timpi omologi, fiecare marime fizica trebuie sa determine, prin valorile ei de pe prototip si de pe model, un raport constant, independent de alegerea punctelor omologe. Toate aceste rapoarte se numesc rapoarte de similitudine, sau scarile marimilor fizice. Ca si marimile fizice, scarile pot fi fundamentale si derivate. Scarile marimilor fundamentale se numesc scari fundamentale, iar scarile marimilor derivate se numesc scari derivate. In sistemul S.I. sunt deci sase scari fundamentale: - O - pentru lungimi;
P - pentru mase;
W - pentru timpi;
D - pentru intensitatile curentilor electrici;
T - pentru temperatura si
Ventilatoare, suflante, turbocompresoare
G pentru intensitatile luminoase.
Avānd aceeasi structura ca si relatiile de definitie ale marimilor derivate, scarile derivate - notate prin litera k īnsotita de indicele, care precizeaza marimea derivata respectiva - se pot stabili usor īn functie de scarile fundamentale.
De exemplu scarile pentru viteza, forte si debite se obtin imediat scriind:
k v = vn = tn = lm = O
tm tm
k a = antn2 = lm O
kF= Fn = mn an P O
Fm mm-am W
ln3 ln3
|
Vn t lm3 O Vm lm3 tn W |
kV V = n = m = -
lm
tm tm
2.2.1. Analiza criteriilor de similitudine
2.2.2.1. Criteriul lui Newton
In teoria similitudinii, alaturi de scari, se folosesc, de asemenea, si marimile complexe, adimensionale, care se pot forma din marimi fizice care intervin īn structura fenomenului. Aceste marimi complexe se numesc criterii de similitudine sau invarianti de similitudine si poarta numele savantilor care au lucrat īn domeniul respectiv al stiintei. O proprietate fundamentala īn teoria similitudinii este ca īn fenomene asemenea criteriile de similitudine au aceleasi valori numerice pe model si pe prototip. Analizānd, de exemplu, criteriul de similitudine al lui Newton, care se refera la similitudinea fortelor de inertie vom pleca de la legea a-II-a a mecanicii clasice:
F m-a Scara fortelor de inertie este deci:
|
kF=kmka=P |
O
W
Ventilatoare, suflante, turbocompresoare
Daca īn acesta relatie se īnlocuiesc scarile prin valorile lor:
se obtine:
mn P
mm
ln O
lm
tn W
tm
Fn Fm
|
mm |
ln mn lm
tn
V m J
sau:
Cum m U-V U-l, U retranscrisa si sub forma:
|
Fm-t2 |
|
|
Fn tn2 =
mn-ln mm-lm fiind densitatea si V volumul, ecuatia precedenta poate fi
|
|
Fn-t2n
|
|
Un-lm
U m m
|
Fn |
Fm
Unln2-vn2 Um-lm vm2
Ne
Relatiile (34), (35), (36) reprezinta sub diferite forme, criteriul de similitudine al lui Newton; ele ne arata ca īn fenomene asemenea, īn ce priveste fortele de inertie, criteriul lui Newton are aceeasi valoare numerica pe model si pe prototip.
2.2.2.2 Criteriul Reynolds
Pentru deducerea expresiei matematice a acestui criteriu, putem pleca de la scara vāscozitatilor cinematice Q , care se masoara īn m2/s.
|
kQ n |
Qn O Q m W
avem:
Inlocuind scarile fundamentale prin marimile omoloage de pe model si prototip,
Ventilatoare, suflante, turbocompresoare
|
ln2 |
ln Xn lm2 ln2 tm
|
t |
Xm tn tn lm
m
ln lm
Cum vn= n si vm= m , se
poate scrie:
tn tm
Xm vm-lm
de unde rezulta criteriul lui Reynolds:
X m X m
care pentru Xm Xm obtinem:
vn'lm=vm 'lm sau O2 W
nm mm
Se observa usor ca valoarea criteriului Re este direct proportional cu raportul dintre forta de inertie si forta de vāscozitate. Intradevar, īn baza formulei (36), forta de inertie are expresia:
Fi kU l v2
In ceea ce priveste forta de vāscozitate, aceasta se obtine din formula lui Newton:
dv v
FQ KA KA
dy l
K Inlocuind A=l2 si X se obtine:
U
Fi kU l2v2 vl
=k= k Re
Fv UXlv X
ce ne permite sa apreciem care din aceste doua categorii de forte au un rol proponderent īn evolutia fenomenului.
Cu cāt numarul Re este mai mic cu atāt influenta vāscozitatii asupra miscarii fluidului este mai mare. Pentru un Re foarte mare, rolul preponderent īl au fortele de inertie. In fenomene asemenea, īn ceea ce priveste fortele de vāscozitate avānd Ren=Rem, pe baza ecuatiei (39) putem scrie egalitatea:
Ventilatoare, suflante, turbocompresoare
FF
in im
= FF
vn vm
sau:
FF
in = vn
FF
im vm
care conducānd la criteriul de similitudine Newton, exprimat prin ecuatia (36), ne arata ca similitudinea fortelor de vāscozitate este realizata simultan cu similitudinea fortelor de inertie, ele avānd aceeasi scara.
2.2.2.3 Criteriul de similitudine al lui Mach
Daca raportul de comprimare realizat de turbocompresor depaseste o anumita valoare (p2/p1>1,05) atunci densitatea fluidului īn diferite puncte ale compresorului nu mai este constanta. De aceea, pentru ca doua turbocompresoare diferite sa aiba o similitudine perfecta a curgerii, trebuie ca raportul densitatilor fluidului īn punctele omologe ale celor doua sisteme sa fie aceeasi. Numai īn acest caz cele doua rapoarte de comprimare sunt egale, adica:
pp
2n 2m
= pp
1m 1n
Cum īntr-un mediu elastic viteza sunetului, notata cu a, este legata de densitatea U a mediului prin formula lui Newton,
a=
U \
dp =4kRT
dU
unde: K - modulul de elasticitate;
k - exponentul adiabatic; R - constanta gazelor; T - temperatura absoluta. Pentru cele doua medii elastice se poate scrie raportul:
kn Un an2
km Umam2 care conduce la criteriul de similitudine Mach:
|
vn vm am |
vn vm
M
an am
Ventilatoare, suflante, turbocompresoare
unde vnsi vm reprezinta vitezele curentului de fluid pe prototip, respective pe model.
2.2.3. Coeficientul de debit M
Exploatarea unei turbomasini poate fi privita din doua puncte de vedere si anume:
pastrānd sectiunea de aspiratie constanta si variind turatia si
pastrānd turatia constanta si variind sectiunea de aspiratie prin laminare.
In primul caz avem coeficient de debit M si īn al doilea caz coeficientul de sarcina
Coeficientul de debit este definit, īn general, ca fiind raportul dintre o viteza de curgere, caracteristica fluidului de lucru, notata cu u' si o alta viteza de rotatie caracteristica unui organ de masina (rotor), notata cu u.
Deci:
M
u
Viteza de curgere u' este obtinuta din raportul dintre debitul aspirat pe secunda V si o suprafata de curgere a fluidului, caracteristica compresorului, notata cu A.
Deci:
uc V
A
sau:
M VV^2
unde u2 este viteza periferica a rotorului cu raza r2, iar A este suprafata la iesirea din rotor. Pastrānd aceeasi deschidere a vanei de aspiratie, dar micsorānd turatia, fara a lua īn considerare frecarile si compresibilitatea gazului, starile noi create sunt asemenea īntre ele, adica au acelasi M deoarece debitul V se micsoreaza (variaza) īn acelasi raport cu viteza periferica u2.
2.2.4.Coeficientul de sarcina
Ventilatoare, suflante, turbocompresoare
In timp ce coeficientul de debit M caracterizeaza o stare cinematica a unei
turbomasini, coeficientul de sarcina caracterizeaza o stare dinamica. Expresia sa se
deduce din criteriul de similitudine al lui Newton. Fie o forta F sau o componenta a fortei dupa o directie anumita, care actioneaza asupra unui sistem solid sau fluid. Atunci pe baza relatiei (36) coeficientul de sarcina va fi:
F kp= 2 Uv A
care are aceeasi valoare pentru toate sistemele dinamice asemenea.
Se obtine o foarte importanta marime caracteristica pentru turbomasini, daca se īnlocuieste raportul F/A prin diferenta presiunilor totale ptot, dupa si īnaite de turbomasina, si viteza v cu o viteza caracteristica - u a organelor īn miscare, numit coeficient de presiune:
p
tot
U u 2
Pentru diferentele mici de presiune Ap se scrie:
Ap = gUHad si devine:
gHad
u 2
La rapoarte de comprimare, la care compresibilitatea nu mai poate fi neglijata, relatiile (45) si (46) dau rezultate diferite. Dupa cum au aratat cercetarile facute asupra turbocompresoarelor axiale si centrifugale ultima expresie este mult mai utilizata, īn timp ce prima expresie īsi gaseste aplicarea numai īn unele cazuri speciale, unde diferenta de presiune este foarte mica. Trebuie remarcat faptul ca Had are īn relatia de mai sus dimensiunea unei lungimi, care corespunde lucrului mecanic consumat. Daca cu Had se noteaza lucrul mecanic consumat, īn J/kg , atunci
devine:
2Had
u 2
Coeficientul de sarcina este functie de starea de laminare a turbomasinii, caracterizata prin coeficientul de debit M si de aceea se pote reprezenta īntr-o diagrama M
Ventilatoare, suflante, turbocompresoare
Aceasta diagrama este valabila nu numai pentru cercetarea turbomasinilor sau turatiilor, ci si ca o metoda de aproximare pentru toate turbomasinile geometric asemenea, la turatiile dorite, atāta timp cāt mediul este considerat practic incompresibil sau considerānd ca au acelasi numar Mach la un Re foarte mare.
2.2.5. Coeficientii adimensionali M si \ īn cazul turbomasinilor 2.2.5.1. Compresoare axiale
La compresoarele axiale īn general coeficientul de debit M se defineste ca raportul dintre viteza axiala, la intrarea in rotor v, si viteza periferica a rotorului u2.
Deci:
v?L = V
u2 A-u2
unde: - Vas [m3/s] este debitul la intrarea īn turbomasina, dedus din starea statica la intrarea īn rotor;
A = (d - d12) - d22 1 - X [m 2 ] - sectiunea inelara la intrarea īn rotor;
Q raportul diametrelor;
d2
d1 [m] - diametrul butucului rotorului;
vm = Vs. [m/s] - componenta medie axiala a vitezei de curgere la intrarea īn rotor;
u S d2n [m/s] - viteza periferica a rotorului, dedusa cu diametrul exterior
60
d2.
In unele cazuri coeficientul de debit este definit īn functie de debitul volumic la
intrarea īn rotor, dedus din starea totala, Vatot si se noteaza cu M*
= V^.1
d 2 u 2
4 2
|
U tot |
Us
Ventilatoare, suflante, turbocompresoare
unde Ua Utot este raportul densitatilor. Cu aceasta:
|
Ua |
|
1-X2) |
M =M
|
tot |
U
corespunzator pentru coeficientul de presiune , conform relatiei (47) se obtine:
2Had u22
2.2.5.2 Compresoare centrifugale
La compresoarele centrifugale si diagonale se poate arata ca:
4 2
si M* V.1
|
|
S d u
|
ad |
2H
u22
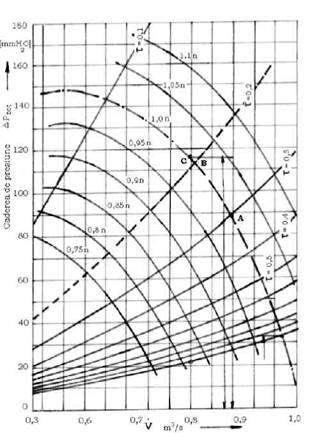
Fig. 2.1 Relatia dintre caderea totala de presiune si debit la diferite tura tii
Ventilatoare, suflante, turbocompresoare
2.2.6. Coeficientul de strangulare W
Asa cum s-a amintit la paragraful 1.3 functionarea turbocompresorului poate fi aratata īntr-o diagrama īn care caderea de presiune este functie de variatia debitului.
Relatia īntre caderea de presiune si debit, considerānd turatia constanta este reprezentata sub forma curbei caracteristice, asa cum se indica īn fig 2.1
Daca īntr-un turbocompresor se modifica rezistentele de curgere se schimba si rapoartele de comprimare. Aceste rezistente pot fi modificate prin reglarea clapetei unei vane, care conduce la modificarea debitului, dar mentinand turatia constanta. Pentru diferitele pozitii ale clapetei se obtin diferite valori pentru M si
Unei perechi de valori (V si Aptot) īi corespunde un singur punct īn diagrama
Aptot-V. Modificānd pozitia clapetei se obtin alte perchi de valori (Aptot,V) care
reprezentate īn diagrama dau nastere la curba 1. Aceasta curba a fost denumita curba caracteristica sau de strangulare. Sub denumirea de curba caracteristica se īntelege o
curba īn coordonate (Aptot,V) care reda starile de exploatare variabile ale unue
turbomasini la o turatie constanta si la un unghi de atac al paletei constant.
Turatia n1 se considera ca parametru a curbei caracteristice. Prin mentinerea constanta a deschiderii clapetei si prin variatia turatiei la n2 se obtine o alta curba caracteristica. Aceste doua curbe sunt asemenea deoarece procesele de curgere la cele doua turatii sunt la fel asemenea. In acest caz compresorul trebuie sa creeze o presiune totala Aptot, care reprezinta suma presiunii dinamice cu viteza vmA si a pierderilor de presiune īn coturi, conform relatiei:
4ptot = U vmA+Z^U£
i=l 1
unde w este un coeficient de rezistenta si este considerat constant, deci independent de numarul Reynolds.
Cāt priveste densitatea U - si ea a fost considerata constanta. Ca urmare caderea de presiune Aptot este functie de patratul vitezei vm .
Relatia de mai sus poate fi pusa sub forma:
Ventilatoare, suflante, turbocompresoare
U
|
tot |
pt
Vva
A
Apt
tot
U
|
v |
|
V |
tot
A
2H
ad
W
Acest raport notat W este denumit coeficient de strangulare si depinde numai de pozitia clapetei vanei de reglare.
Locul geometric al tuturor punctelor cu W = const. conform ecuatiei (55) este o parabola, care se poate calcula daca se cunosc coeficientul de debit M si sectiunea A.
Pe aceasta parabola se gasesc toate acele puncte de stare ale compresorului care pot fi obtinute prin pozitia clapetei cu W = const. la turatie variabila. Daca pozitia clapetei este reglata īn trepte atunci se obtine o retea de curbe W = const., ca īn fig. 2.1. Punctele de pe curbele W , care apartin aceleasi turatii pot fi unite, obtināndu-se asa numita curba de turatie si prin variatia īn trepte se obtin curbele cu n = const.
Conform acestei constructii un punct de pe diagrama se poate caracteriza īn felul urmator: - punctul de exploatare considerat este intersectia curbei W =const., apartinatoare unei anumite pozitii a clapetei cu curba n = const., apartinatoare curbei de turatiei.
Pentru W 1, relatia (55) devine:
U ptot = vm 2
Pentru punctu c de pe curba n1=const., se poate obtine prin intersectia verticalei ce trece prin punctul c cu curba W 1, presiunea dinamica:
U pd
Ecuatia (55) se poate pune īn functie de coeficientii adimensionali M si\ īn modul urmator:
|
V 'va |
|
V va V A J |
|
M |
|
|
|
|
|
W |
|
|
|
pt |
|
tot |
|
U |
A-u2j 2 2
Cu aceste valori M si se intocmeste o noua diagrama īn care sunt trasate si curbeleW
Ventilatoare, suflante, turbocompresoare
Considerānd pe W const. si variind pe n din relatiile de definitie a lui M si
pto
si
tot
|
Au2 |
U u2
rezulta ca acesti coeficienti īn acest caz sunt independenti de turatie. Curba de strangulare W = const. se schimba nu numai cu turatia, dar īn primul rānd de orientarea paletei, deci īn diagrama M-\ parametrul curbei de strangulare nu este
turatia n, ci unghiul de reglare al paletei G
Avantajul diagrameiM-\ fata de diagrama Aptot- V consta īn faptul ca doua curbe diferite 1 si 1' din diagrame M-\ pot fi gasite īn diagrama Aptot- V , numai īntr-o singura curba. Aceasta īnseamna ca īn diagrama Aptot- V, pot fi gasite numai punctele de exploatare mai importante, pe cand celelalte puncte nu.
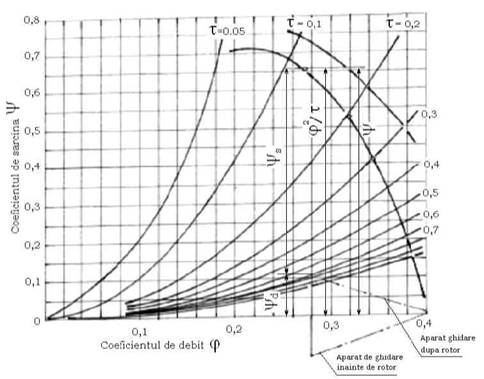
Fig. Coeficientul de sarcin a \ īn functie de coeficientul de debit M
Ca urmare coeficientul de strangulare W este un numar caracteristic si are o mare īnsemnatate īn dezvoltarea ulterioara a turbocomasinilor si īn special al compresoarelor axiale.
Acest coeficient W este calculabil daca se cunosc debitul V caderea de presiune Aptot, respective sarcina Had si aria A
Ventilatoare, suflante, turbocompresoare
2.2.7.Coeficient de rapiditate V
Stiind ca sarcina Had sau caderea de presiune Aptot, debitul V si turatia n
influenteaza constructia compresorului, este normal ca sa se caute un numar caracteristic pentru fiecare tip constructiv care sa cuprinda aceste marimi. Este de dorit ca din aceasta combinatie sa rezulte un numar adimensional numit "numar specific de turatie" notat cu K. Tinānd cont si de compresibilitatea agentului de lucru, prin densitatea U , aceasta combinatie este:
|
K= |
D
.QE .nJ =HEad.VE .nJ
Deoarece acest numar trebuie sa fie adimensional se vor determina exponentii D E si J din ecuatia de dimensiune:
V s J
E
J
Expresia de mai sus devine adimensionala daca:
2D + 3E = 0 2D + E J
Daca se alege J =1, numarul caracteristic cautat trebuie sa fie proportional cu
turatia. Acest lucru se obtine daca:
2D+E = - deci ca urmare relatia (58) se pune sub forma:
E =
si
D = -
|
|
K = Had -V2-n
Utilizānd coeficientii de debit M* si de presiuni , definiti conform relatiilor (44) si (45) relatia (60) devine:
|
S d V |
2V4
|
|
|
\-u |
|
60-u2 S d |
|
const.iM*\2 |
|
K |
S-d M -u2
V
Coeficiertul de rapiditate īn cazul general se defineste prin:
d
|
|
M*2.
Ventilatoare, suflante, turbocompresoare
Prin explicitare relatia (61) devine:
|
|
V =
|
|
|
V |
|
ad |
|
|
2H
|
u |
KAu2j v j
V2{2Had)-4.u2
d
S-n-d2
|
|
d2
V2-Ha d =
0.3251-n-V2.Ha d
In multe lucrari de specialitate īn locul de coeficientul de rapiditate V deteminat prin relatia (62) se utilizeaza asa numita turatie specifica, data de relatia:
|
|
ns =
n-V2-Ha d
(62a)
O alta marime caracteristica derivata din cea anterioara este asa numitul diametru adimensional definit prin:
U 1
A = S.(2Had)4.V2-d2
(62b)
Legatura dintre coeficientul de strangulare W si diametrul adimensional A se determina daca se utilizeaza īn relatia (62a) coeficientul de debit M* si de presiune\ .
|
|
\
|
M |
M J
Deci diametrul adimensional este o valoare caracteristica a coeficientului de strangulare W
Pentru compresorul axial īn mod obisnuit coeficientul de debit se pune M si coeficientul de rapiditate V poate fi pus sub forma:
vm u2
|
|
|
|
|
U s I |
|
V |
M 1-X2)
U
\ tot J
Mai simplu se poate defini un alt coeficient de rapiditate de forma:
|
_3 |
|
U tot Us |
|
Va=M~2-\ |
|
|
V
Ventilatoare, suflante, turbocompresoare
Aceaste marimei caracteristice sunt reprezentate īntr-o diagrama īn care se pot vedea legaturile dintre sarcina, debit si turatia īn cazul turbocompresoarelor, asa cum rezulta din fig. 2.3.
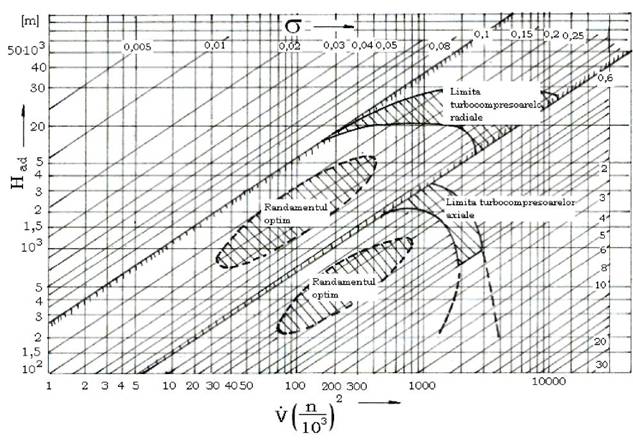
Fig. 2.3 Domeniul de lucru al turbomasinilor axiale si radiale
Din figura se mai vede domeniul randamentelor optime pentru cele doua tipuri de compresoare, precum si limitele utilizarii acestora īntr-o treapta sau duoa trepte. Zona hasurata reprezinta domeniul limita īn care pot fi utilizate compresoarele atāt īntr-o treapta cāt si īn doua trepte.
2.3. Definire numerelor caracteristice pentru turbomasinile īn mai multe trepte
Deoarece raportul de comprimare īntr-o trepta este destul de redus la turbocompresoare si cum īn practica se cer presiuni din ce īn ce mai mari, deci rapoarte de comprimare ridicate se recurge la comprimarea īn trepte.
Asa la comprimarea īntr-o trepta s-au definit coeficientii de debit M , de sarcina V la comprimarea īn trepte se pot stabili īn acelasi mod acesti coeficienti.
Ventilatoare, suflante, turbocompresoare
Daca se considera sarcina adiabatica ca fiind aceeasi pe toate treptele si numarul treptelor este z1, sarcina adiabatica totala va fi:
H zH
ad adtr
Coeficientii M si V la comprimarea īn trepte sunt deci:
V
|
S■d2 u2 |
M*=V- -
2Ha
2Had
u2
V 0.0351-n-V2.Ha d
Intre coeficienti pe treapta si coeficientii globali (pe masina ) exista relatiile:
M tl = M*
tr
z1
Vtr=z14-V
2.4. Definirea numerelor caracteristice īn cazul legarii īn paralel a mai multor
trepte
In cazul cānd debitul cerut este foarte mare se recurge la cuplarea īn paralel a mai multor trepte de acelasi fel.
In acest caz se scrie:
-debitul total:
V = z2Vtr unde z2 este numar de trepte legate īn paralel.
sectiunea totala:
A = z2Atr
coeficientul de debit total:
Ventilatoare, suflante, turbocompresoare
M =
V____ 1
'u2
d22
-coeficientul de sarcina :
2Had u22
-coeficient de rapiditate :
|
|
|
V 0.0351-n-V2-H4 |
|
ad |
Relatiile īntre
coeficientii M \ si V pe treapta si
globali sunt:
M tr M, \tr=\ ,Vtr=V 1
2.5. Dependenta īntre numarul de treptez1 si numarul de trepte legate īn paralel
z2
|
|
Fig. 2.4 Numarul de tepte īn functie de coeficientul de rapiditate
Considerand ca avem un agregat care are z1 trepte legate īn serie si z2 trepte legate īn paralel, identice, atunci se pot scrie relatiile:
V = z 2 V tr r A = z 2 A tr H ad = z 1 H adtr
|
2Had ; |
|
u |
M* =
V
|
u2 |
Au
|
M |
V z2 ■
Ventilatoare, suflante, turbocompresoare
Relatiile īntre cele doua sisteme de cuplare a treptelor īn serie si īn paralel
sunt:
|
4 adtr |
M t
M*,
t
z1
|
z22 |
H4
Pentru calculul practic al numarului de trepte z1, s-a īntocmit diagrama din figura 2.4. īn care z1 rezulta īn functie de coeficientul de rapiditate V si de tipul constructiv al turbomasinii.
Ventilatoare, suflante, turbocompresoare 3. PRINCIPIILE FUNDAMENTALE TURBOCOMPRESOARELOR
3.1.Geometria curgerii īn turbomasini 3.1.1 .Triunghiul vitezelor
La toate turbomasinile se deosebesc urmatoarele viteze:
-viteza relativa w ;
-viteza periferica u ;
-viteza absoluta v .
Viteza relativa w, este viteza fata de sistemul de coordonate mobil al sistemului.
Viteza absoluta v este considerata fata de un sistem de coordonate fix.
Pentru a īntelege mai bine acest lucru folosim figura 3.1., cānd un vehicul se deplaseaza cu viteza u. In vehicul, un om se deplaseaza relativ cu o viteza w fata de vehiculul īn miscare.
Adunānd viteza w a omului, care este relativa fata de vehiculul īn miscare, cu viteza u a vehiculului, care si ea este relativa fata de pamānt, se obtine viteza v. Se observa ca viteza absoluta v este suma vectoriala a vitezei relative w si a vitezei de īnaintare u.
Deci:
v=u+w,
sau w = v-u
(vitezele v si u se pot masura)
Revenind la cazul turbomasinilor, se considera o masa elementara de gaz cu viteza relativa w fata de rotorul cu viteza periferica u, si se obtine viteza absoluta v a masei elementare. Viteza periferica u (de īnaintare) depinde de raza rotorului.
3.1.2. Reteaua de palete
La turbomasini, curgerea fluidului se face printr-o retea de palete, care pot fi ordonate sub forma de sir de palete sau de gratar de palete. La turbomasinile radiale paletele sunt dispuse radial, gratar radial, cuprinzānd īntre ele canale, care se rotesc odata cu paletele.
Trecerea masei de gaz prin reteaua rotitoare pretinde o expunere matematica laborioasa, deoare curgerea relativa este turbionara. De altfel, o metoda de calcul aerodinamica a gratarului rotitor nu exista.
Ventilatoare, suflante, turbocompresoare
|
|
|
|
Fig. 3.3 Triunghiul vitezelor īn cazul rotorului Fig. 3.2 Triunghiul vitezelor īn cazul rotorului
axial radial
S-au studiat rotoarele radiale cu palete drepte, apoi sub forma de spirala logaritmica si īn arc de cerc.
Studiul gratarului circular s-a realizat cu ajutorul paletei drepte, pentru a idealiza curgerea īn compresorul axial.
La rotorul radial miscarea ideala se compara cu gratarul drept, care are numai o miscare de translatie.
3.2. Legile mecanice ale turbomasinilor
Calculul turbomasinilor se bazeaza pe legile mecanice si anume:
ecuatia lui Bernoulli;
legea impulsului (momentului rotitor);
ecuatia de continuitate.
3.2.1. Ecuatia generalizata a lui Bernoulli
Pentru curgerea compresibila, fara pierderi, avem relatia:
v2+\p stat dp+gh = const.
2 }p tot U
unde: ptot const.
Ventilatoare, suflante, turbocompresoare
Termenul (gh), care reprezinta influenta īnaltimii geodezice, fiind mic īn comparatie cu celelalte marimi, poate fi neglijat. Variatia densitatii U cu presiunea p
se poate arata considerānd o transformare adiabatica pvk const. si īn acest caz este valabila relatia:
|
k | = k |
|
Rttot |
|
RTst |
|
k-1 |
v2 k
r
|
pt |
p stat
|
L |
tot y
|
tot |
|
p |
pt
\pstat J
k-1
k
De aici rezulta:
p
|
tot |
stat
pt
v2 k-1
2* k 'RTtoty
|
tot |
pt
1_v2 kz1
k
a - VkRT - viteza sunetului (īn stare totala sau statica)
|
|
|
|
|
v2 k-1 |
|
p |
|
ptot p |
|
|
|
const. |
v2 k-1 1 2" k "R-Tstat,
|
stat |
|
stat |
a2 2
Diferenta dintre presiunea totala si cea statica o constituie presiunea dinamica:
p din=p tot~p stat La variatii mici de presiune, pentru care variatia densitatii este neglijabila, expresia de mai sus poate fi pusa sub forma:
|
p stat |
Uv2
|
tot |
pdin=ptot~p
3.2.2. Legea impulsului sau a momentului rotator
Pentru a se putea stabili expresia presiunii teoretice create de compresor (caderea teoretica), se pleaca de la momentul motor M, care se aplica asupra rotorului, si care este echilibrat de momentul fortelor ce iau nastere īn paletele si pe suprafetele inferioare ale rotorului, datorita fluidului care curge prin el.
Avānd o curgere ideala, se considera ca energia furnizata de motorul de antrenare se transmite uniform fiecarei particule de fluid. Considerānd ca miscarea fluidului, de la intrarea īn rotor si pāna la iesirea din el, se face dupa o paleta de forma oarecare, directia de curgere este īntotdeauna tangenta la paleta.
Pentru a stabili expresia momentului motor care se aplica rotorului, se recurge la triunghiurile vitezelor, de la intrerea si iesirea din rotor, figura 3.4.
In aceasta figura starea 1 arata intrarea fluidului īn rotor si starea 2 iesirea fluidului din rotor. Traiectoria de la 1 la 2 este profilul paletei pe care se deplaseaza fluidul, avānd directia de miscare tangenta la paleta.
Ventilatoare, suflante, turbocompresoare
|
|
Fig. 3.4 Triunghiurile vitezelor la intrarea si iesirea din rotor
La triunghiurile vitezelor se deosebesc:
-u1 si u2 - vitezele periferice la intrarea, respectiv iesirea din rotor;
-v1 si v2 - vitezele absolute la intrarea, respectiv iesirea din rotor;
-w1 si w2 - vitezele relative la intrarea, respectiv iesirea din rotor;
-v1u si v2u - componentele vitezelor absolute dupa directia vitezelor periferice (tangente la doua cercuri cu razele r1 si r2);
-v1r si v2r - componentele vitezelor absolute dupa directia radiala (meridiana);
Se vede ca directia de miscare este data de viteza ralativa w, care īn cele doua stari are valorile w1 si w2.
r1 si r2 - razele interioara respectiv exterioara ale rotorului;
D 1 si D2 - unghiurile dintre vitezele v1 si u1 respectiv v2 si u2;
-E 1 si E2 unghiurile dintre vitezele w1 si u1 respectiv w2 si u2.
In ipotezele ca exista regim permanent de curgere, fluid ideal, curgere ideala si cu notatiile de mai sus se stabileste relatia de baza, aplicand teorema impulsului sau a cantitatii de miscare:
M = m(v2ur2-v1ur1) [ J]
unde :
|
2ur2 - momentul cantitatii de miscare la iesirea din rotor, m v1ur1 - momentul cantitatii de miscare la intrarea īn rotor. |
|
m v |
m - este debitul masic de fluid [kg/s],
Ventilatoare, suflante, turbocompresoare
2.3.3. Ecuatia continuitatii
Ecuatia continuitatii corespunde legii conservarii masei, ceea ce īn cazul turbomasinilor arata debitul masic.
m = V U A ■ v ■ U =const. [kg/ s]
Daca se logaritmeaza ecuatia (85) si se diferentiaza se obtine, ecuatia continuitatii sub forma diferentiala:
dA+dV+d U=0 (85a)
A V U 3.2.4. Ecuatiile principale ale turbomasinilor
Pentru a arata variatia energiei consumate de momentul motor M, se considera ca aceasta energie se poate compara cu lucrul mecanic necesar pentru a ridica masa m de fluid la o īnaltime H, care se va numi īnaltime teoretica de refulare, sau cadere teoretica. Pentru a ilustra ca este vorba de cazul teoretic, cu un rotor cu numar infinit de palete, aceasta īnaltime teoretica devine Htf. Aceasta īnaltime Htf poate fi
exprimata īn functie de variatia presiunii produsa īn coloana de fluid, considerānd densitatea U const.
Ap = U-g-H [N/m2]
Aceasta expresie este valabila pentru cazul cānd U variaza foarte putin (cazul
ventilatoarelor).
Considerānd viteza unghiulara Z constanta se poste exprima puterea
consumata:
|
p tot |
P = MZ = m Z v2ur2-v1ur1) = mgHtf=mApt
, [W]
dar:
Zr2=u2;
Zr1=u1
Deci:
|
m- |
|
m |
m-g-Htf=m-
Z
v
2u
|
1u |
u2 u1
|
Z |
Z
■g-Ht^m-(v2uu2-v1uu1)
de unde:
Htf =-{v2uu2-v1uu1), [m]
Ventilatoare, suflante, turbocompresoare
Caderea de presiune Ap, pentru U const. devine:
bptot=gUHt^Uv2uu2-v1uu1), [N/m2]
De aici rezulta:
a. caderea Htf, este
independenta de densitate U, deci
este aceeasi pentru
lichide, sau gaze īn conditii identice.
b. caderea Htf,
la viteze tangentiale egale u2=u1=u,
īn cazul compresoarelor
axiale, depinde numai de v2u, respectiv v1u si
atunci:
|
g |
Htf
1 u{v2u-v1u) = uAvu=uAwu, [m]
|
g |
g
caci:
v2u-v1u=w2u-w1u=Awu
c. caderile de presiune sunt proportionale cu densitatea īn aceleasi conditii de viteza si la diametre egale. (daca se considera ca densitatea U este variabila)
pa Ua
|
|
'pb Ub
Expresia lui Htf care cuprinde produsele v2uu2 si v1uu1, necesita o analiza mai
amanuntita si de aceea se considera triunghiurile vitezelor la iesire si la intrare, carora li se va aplica legea cosinusului si se obtine:
w
(u2"v2J
v
2r
w
u2
2u
~2u2v2u
v
2r
dar:
v
2u
v2
cosD
v
2r
v2
sinD
deci:
|
|
w22=u22+v22cos2D2-2u2v2cosD |
|
|
w22=u22+v22-2u2v2cosD2 |
|
la fel si pentru w1: |
|
|
|
w =u2+v12_ 2u1v1cosD1 |
|
Revenind la relatiile (82) si (83) se obtine: |
|
|
|
w =u12+v12-2u1v1u |
|
|
w22 =u22+v22-2u2v2u |
|
de unde: |
|
|
|
u1v1u=1{u12+v12-w12) |
v22sin2D2
Ventilatoare, suflante, turbocompresoare
u2v2u=u22+v22-w22)
Aceste relatii īnlocuite īn (88) duc la:
Htf 1[(v2 -v12)+(u22 -u12)+(w22 - w2)],[m]
Relatiile (88) si (96) reprezinta lucrul mecanic. Daca procesul se refera la masa de 1kg de fluid, atunci expresiile (88) si (96) devin:
Ht f =g-Htf= (v2uu2 -v1uu1), [J/kg]
Ht f =g-Htf = -[(v2 -v12)+(u22 -u12)+(w22 - w2)]
AiciHtf reprezinta lucru mecanic īn J/kg, iar Htf reprezinta īnaltimea īn [m] Caderea de presiune va fi:
Aptot = U [(v2 _ v2)+ (u22 - u12)+ (w22 - w12)] [N/m]
sau:
4ptot = U(v2uu2-v1uu1,[N/m2]
Din expresiile (98) si (99) se pot face urmatoarele consideratii:
a) termenul -(v2 -v2) respectiv U(v2 -v2 )reprezinta energia cinetica pentru 1kg
de fluid la iesirea din rotor. Aceasta energie cinetica creaza o presiune (cadere) statica īn difuzor, dupa ce fluidulul a parasit rotorul si se obtine prin micsorarea vitezei, agentul fiind trecut prin sectiuni variabile corespunzatoare, conform ecuatiei (85).
Presiunea astfel obtinuta, īn difuzorul masinii formeaza presiunea dinamica si se noteaza cu Hdf.
b) al doilea termen -iu22 -u12) respectiv U u22-u12) indica o energie potentiala
care se transforma īn presiune statica īn rotor, datorita fortelor centrifugale.
Pentru a arata efectul fortelor centrifugale asupra fluidului dintre palete, se considera un canal de grosime infinit mica, plin cu fluid, avānd intrarea si iesirea īnchisa. Se mai considera ca īn acest canal rotoric, din cauza dimensiunilor lui mici nu se mai poate dezvolta o miscare relativa a fluidului īn canal si fluidul se comporta ca un corp solid, īn care se dezvolta forte centrifugale, care produc o crestere a presiunii.
Forta centrifugala ce se dezvolta īntr-un element de volum infinit mic este:
dF^dr-ds-b-U-r-Z2 , [N]
īn care b este adāncimea canalului rotoric.
Ventilatoare, suflante, turbocompresoare
|
|
Fig. 3.5 Gradientul de presiune datorat fortelor centrifuge
Aceasta forta dFc, dezvoltata īn element, exercita o presiune spre exterior si este echilibrata de o alta forta egala si de sens contrar, de forma:
dFc=ds-b-dp Scriind conditia de echilibru rezulta:
ds-b-dp = dr.ds-b-U-r.Z2 dp = Z2-U-r.dr sau:
![]() r2
r2
p = \dp = UZ2\r.dr = UZ\r 2-r 1
V
, [N/m2]
[N/m 2 ]
Considerānd aceasta cadere partiala:
|
2 t f=-u22-u12)[m] |
Ap = g-U-H'tf=U u22-u12), [N/m 2 ]
Htf= - {u22-u )[m]
sau pentru 1kg de fluid:
H' = gH'tf = -(u22 -u12) ,[J/kg]
Aceasta energie potentiala se transforma īn presiune statica īn rotor, asa cum s-a
|
sf |
aratat, datorita fortelor centrifugale si se noteaza cu H'
Ventilatoare, suflante, turbocompresoare
c) al treilea termen (w2-w2) respectiv U(w2-w2) este o energie potentiala
2V 1 2\
produsa īn rotor deoarece w1 > w2.
Daca se admite ca īntre paletele rotorului se produce o curgere permanenta, atunci pentru un kg de fluid se poate scrie pentru caderea partiala Ap:
|
Ap =U w2-w2, [N/m 2 ] 2V 1 |
U p
sau:
H = -(w12 - w22), [J/kg]
Acest termen reprezinta o energie potentiala, din rotor, care se transforma īn presiune statica din cauza micsorarii vitezei curentului de fluid, la trecerea prin canalele paletate, care, de obicei, se largesc spre exterior.
Ca rezumat al acestei analize se poate conchide ca pentru 1 kg de fluid aflat īn rotor, energia transmisa fluidului se repartizeza astfel:
o parte din energie se transforma īn
energie cinetica a fluidului, care la rāndul
ei se trasforma partial īn presiune statica, īn difuzor. Aceasta
este presiunea dinamica,
realizata īn difuzor. Forma ei este:
Hdf=-v22-v21) [J/kg]
alta parte din energiei se
gaseste sub forma potentiala si se
transforma īn
presiune statica, īn rotor, si are forma:
Hs f u22 -u )+(w -w22)], [J/kg]
sau:
Htf=Hd f+Hs f
Htf - este īnaltimea totala īntr-o treapta. La fel:
Aptot=Apd+Aps
Aptot - reprezinta presiunea totala īntr-o treapta.
Ecuatiile (88), (89), (98) si (110) reprezinta baza studiului turbomasinilor.
Cresterea presiunii īn compresoarele axiale si radiale se face pe seama micsorarii vitezei relative w, a schimbarii vitezei periferice u īn rotor si transformarea energiei cinetice īn energie potentiala īn difuzor.
Pentru a īntelege conditiile de curgere, īn aceste compresoare trebuie observata actiunea frecarii, care cauta sa frāneze curgerea pe suparfetele de contact cu fluid,
Ventilatoare, suflante, turbocompresoare
formānd asa numitul strat limita, care schimba directia de miscare dānd nastere la turbioane. Aceste turbioane pot duce compresorul īn zona de "pompaj'' cānd functioanarea este neregulata, cu un randament scazut.
La compresoarele centrifugale, pe lānga energia transmisa de palete, mai actioneaza si fortele centrifugale asupra fluidului, din canalele rotorului. Asa se explica stabilitatea functionala a compresoarelor radiale fata de cele axiale. La compresoarele axiale se evita drumul lung al agentului, cu īntoarceri bruste, de aceea randamentul la aceste compresoare este totdeauna mai ridicat decāt la cele radiale.
3.2.5. Ecuatiile lucrului mecanic
|
p tot Vp a tot |
Pentru a ridica presiunea cuAptot a debitului Va se va consuma puterea:
P = Va-Aptot, [W]
sau considerānd debitul m (kg/s)
P = m-Htf, [W]
Din cele doua ecuatii se obtine:
P = m-{u1vlu-ulvlu\ [W]
sau:
P=m[{vl-vl)+(ul-ul)+(wl+wl, [W]
In teoria aripilor portante, ecuatia lucrului mecanic este dedusa pe baza notiunii de ''circulatie '' V care este integrala vitezei fluidului pe o curba īnchisa.

Fig. 3.6 Circulatia pentru o retea de tip axial
Ventilatoare, suflante, turbocompresoare
Consideram un gratar de palete, al unui rotor axial, din care se limiteza o suprafata ABCD, asa cum arata figura 3.6.
Suprafata considerata este simetrica fata de axa gratarului. Liniile AB si CD sunt paralele iar curbele BC si DA sunt duse la distanta t, ceea ce reprezinta pasul de paletare. Circulatia pe curba īnchisa ABCD este definita ca fiind:
unde v si ds sunt vectorii vitezei absolute respectiv al spatiului parcurs.
Integrala de contur §vds se poate reprezenta ca o suma de integrale partiale:
lvds = \B vds + \C vds + \D vds + \A vds
J JA JB JC JD
Din motive de simetrie:
\C vds \A vds=0
JB JD
B JD
apoi:
\B Avd G = v2u.t2
D G ds=-v1u.t1
Tinānd cont de aceste precizari TABCD devine:
Aceasta este circulatia pentru o plaleta, iar pentru z palete va fi:
r = z-rABCD=z{v2ut2-v1ut1)
dar:
n r=2S(r2v2u-r1vj sau:
T = -fu2v2u-u1vJ,[m2/s]
Circulatia totala V putea fi dedusa din doua integrale partiale, una īn starea 1 la intrare si una īn starea 2, la iesirea din rotor:
T2=z\B Av.ds=2S-r2.v2u
T =z\v.ds = 2S-r1.v1u sau:
r = r,-r,
Ventilatoare, suflante, turbocompresoare
Conform acestei ultime relatii:
H Z.* , [m]
g 2S
Inlocuind īn expresiile (113) si (114), se obtine:
P = nm(*2 *2 )=m Z* [W]
60 gV ' g 2S
|
[W] (115a) |
P = nVaU(*1-*2) = VaU
60 a a 2S
3.3 Legi termodinamice utilizate
Pentru studiul turbomasinilor sunt necesare cunostinte din temodinamica si pentru aceasta se amintesc cāteva mai importante:
3.3.1. Starea normala
Se considera starea normala, starea cu o presiune de 760 mmHg = 1,01325 bar la o temperatura de 0˚C.
3.3.2 Ecuatiile termice de stare
Pentru gazele ideale si practic cu destula exactitate, pentru toate gazele la presiuni scazute si temperaturi mult peste temperatura de fierbere (de lichifiere), se poate utiliza ecuatia:
pv = RT pV = mRT
sau:
pv = - T
M
In cazul vaporilor si al gazelor se utlizeaza tabele sau diagrame.
3.3.3.Entalpia si caldura specifica
Entalpia i a unui kg de gaz este definita prin:
|
i = t cpdt,[J/kg] |
cp
O
si este o marime de stare care depinde, īn general, de presiune si temperatura, iar la gazele perfecte doar de temperatura.
Ventilatoare, suflante, turbocompresoare
cp - este caldura specifica la presiune constanta si la temperatura t [˚C].
Intre entalpie si energia interna u exista relatia:
i = u + pv
Intr-un anumit domeniu de temperatura, caldura specifica poate fi considerata constanta.
i = cpT + const. = cpT
Relatia dintre caldura specifica cp la presiune constanta si caldura specifica la volum constant cv este:
cp-cv=R
In pactica, de multe ori, se utilizeaza caldura specifica molara Mcp = Cp
Cp=Mcp=Mcv+MR = Cv+K = Cv+8314.19 [J/kmol.k]
Cp - caldura specifica molara la presiune constanta; Cv - caldura specifica molara la volum constant; Important este si raportul celor doua calduri specifice:
k = cp
Pentru aerul atmosferic, pāna la 200 [˚C], acest raport poate fi considerat, cu destula exactitate, k = 1.4.
Pentru gazele tehnice acest raport ca si caldurile specifice se dau īn tabele sau diagrame.
Pentru amestecurile lor sunt valabile ecuatiile:
Mcp=YjriMicpi
M-cp M M.cp-8314.19
La turbomasini este foarte importanta vāscozitatea dinamica K īn N/m2 si
|
K vāscozitatea cinematica X īn m2/ s. U |
K
U
Aici U este densitatea fluidului īn kg/m3.
3.3.4. Primul principiu al termodinamicii
La turbomasini acest princiu se utilizeaza, de obicei, sub forma:
q = i2-i1-l, [J/kg]
Ventilatoare, suflante, turbocompresoare
q - caldura introdusa;
i1, i2 - entalpia, īnainte si dupa comprimare;
l - lucru mecanic specific cheltuit.
Aceasta relatie este valabila pentru curentul de fluid, ce strabate masina, īn regim stationar (permanent).
Luānd īn considerare si energia cinetica, relatia devine:
q = i2-
i+
l
|
v2 |
|
Expresia de forma i + |
reprezinta entalpia corespunzatoare presiunii totale, īn
|
|
|
q = h 2tot-h 1tot-l |
|
1tot |
stare adiabatica, a energiei cinetice: unde:
|
|
l = v-dp 3.3.5.Transformari de stare
Calculul termodinamic al turbomasinilor poate fi facut conform transformarilor izotermice, adiabatice si politropice.
-īn cazul iozoterm: T const.; pv const.
liz =p1v1ln v1=p1v1ln p2 R.T1.ln p2 , [J/kg]
|
v2 |
|
p1 |
p1
Liz = mliz =p1V1 ln =p1V1 ln p2 = mRT1 -ln p2 [J/kg]
|
p1 |
v2 p1
-īn cazul adiabatic:
pvk=const.,Tvk1=const.,
T
k-
p k
const.
|
Had |
l ad H adk_1 pvl
k-
k
k
k-1
RT1
p2
k-
k
|
k |
|
|
RfT2-T^cfT2-T^-i1, [J/kg]
k-1 1p2 12 1 q = 0, deorece As = 0
Pentru o evaluare practica se poate utiliza relatia:
Ventilatoare, suflante, turbocompresoare
|
p |
l
ad
RT1
k
k-1
vp1y
k-1
k
- īn cazul politropic:
pvn=const.,Tvn-1=const.,
T p n
const.
l
pol
Hpol
n
n-1
|
|
p1v1
n-1
n
n-1
|
p |
RT1
p2
p1u
n-1 i
[J / kg]
q = 1.nZk.l [J/kg]
n k-1
3.3.6. Curgerea cu frecare
Considerānd o comprimare adiabatica, dar cu frecare, prin introducerea randamentului interior adiabatic Kiad , se poate considera expresia:
T1
p1J
k-1
k
c p-Kwd
|
iad |
Ki
sau:
|
k-1 |
|
k |
|
iad |
K
Se vede ca micsorarea volumului la comprimare cu frecare este mai mica decāt īn cazul comprimarii adiabatice ideale.
Raportul volumelor īn acest caz este:
v1 p2
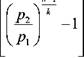 v2 p1
v2 p1
|
K iad |
Ventilatoare, suflante, turbocompresoare
3.4.Termodinamica turbomasinilor
Problema teoretica care se pune īn cazul compresoarelor este aceea a racirii. Compresoarele axiale si radiale, multietajate, īn explatoare pot fi neracite sau racite artificial.
Pāna la un raport de comprimare H 2 , nu se obisnuieste sa se faca o raciere, dar īncepānd cu raportul H 2.5 y3.5 se recomanda racirea. Racirea aduce si unele neajunsuri constructive si de montaj, prin faptul ca se complica constructia statorului prin introducerea canalelor de racire, deci greutate mai mare, apoi agentul de raciere, de regula apa, necesita pompe, eventual o recirculare printr-un turn de racire.
De aceea īnaite de a se aplica racirea se va face un studio amanuntit luānd īn considerare toti factorii care greveaza asupra acestui procedeu si numai īn cazul unei economii, se va aplica.
Sunt si cazuri cānd racirea este necesara, cum este cazul comprimarii gazelor calde, a pompelor de caldura, sau a instalatiilor de distilare prin termocomprimare.
Turbocompresoarele frigorofice se racesc si ele daca e nevoie, dar ca si la compresoarele cu piston racirea poate sa fie facuta fie cu apa sau cu vapori reci din vaporizator.
Sistemul fara racirea turbomasinilor se utilizeaza īn general la urmatoarele locuri:
instalatii cu suflante pentru conditionarea aerului;
instalatii pneumatice;
transportul gazelor, recircularea gazelor īn industria chimica;
alimentarea motoarelor cu ardere interna;
furnale īnalte si oteluri.
Sistemul cu racirea turbocompresoarelor se utilizeaza:
comprimarea aerului pentru unelte pneumatice (5-10 bar)
industria chimica;
industria nucleara;
comprimarea vaporilor īn instalatiile frigorifice;
īncalziri centrale etc.
3.4.1.Turbocompresorul neracit 3.4.1.1. Definitia randamentului īn general
In general un compresor este caracterizat prin presiunea de aspiratie p1 si temperatura de aspiratie T1 a agentului de lucru si de raportul presiunilor p2/p1. In
Ventilatoare, suflante, turbocompresoare
practica, problema care se pune este cāt de mare este puterea consumata pentru comprimarea de la p1 la p2, a agentului de lucru, sau cu alte cuvinte cu ce randament se petrece acest proces de comprimarea īn cazul sistemului fara racire.
Randamemtul unei masini este definit ca raportul dintre puterea efectiva Pe (puterea utila) si puterea consumata la arborele masinii Pc.
n = -
Pa
In cazul turbomasinilor puterea efectiva este puterea necesara procesului de comprimare.
Diferenta dintre aceste doua puteri o constituie pierderile de putere ^APp , asa ca:
Pa=Pef+Y.Pp
Suma pierderilor se poate considera ca fiind formata din trei categorii si anume:
EPp=EPh+EPv+EPm
unde:
a) Y, Ph este puterea pierduta prin asa numitele pirderi hidraulice prin:
frecari pe pereti, la curgerea fluidului prin rotor, difuzor si aparatul director de īntoarcere;
socuri si turbioane pe parcursul curgerii;
transformari incomplete ale energiei īn difuzor.
c) E APv este puterea pierduta prin pierderi volumice prin:
dispozitivul de echilibrare APech;
organele de etansare (APe ).
Suma acestor doua categorii de perechi de pierderi formeaza asa numitele pierderi interioare (APi) care influenteaza procesul de comprimare.
api=EPh+EPv
b) EPm puterea pierduta prin frecari mecanice ale
axului īn lagare (eventual pompe
de ulei actioanate de ax). Aceste pierderi nu influenteaza procesul
de comprimare.
In expresia (135) numaratorul (Pef) poate fi considerat fie ca puterea la arbore (Pa )
minus puterea pierduta prin frecarile mecanice (Pa - APm ) īn care caz raportul:
Pa Pm = Pi = ,
Pa Pa
Ventilatoare, suflante, turbocompresoare
este numit randament mecanic, fie ca numaratorul (Pef) poate sa reprezinte puterea la
arbore (Pa) minus suma tuturor pierderilor ^APp - +£APi + Y,APm si īn acest caz raportul:
P-YAP P
a ^ p = n = K i
Pi Pi
este numit randament interior.
Pu - puterea utila care serveste numai la comprimare propriu-zisa a agentului;
Pi - puterea interioara care serveste la comprimarea fluidului, incluzānd si pierderile teoretice interioare AP Considerānd raportul:
Pu Pi Pu K .Tf=tt
P a P a P a m i K o
care este numit randament total.
|
|
Fig. 3.7 Reprezentarea grafica a puterilor si randamentelor
Numaratorul expresiei (135) depinde de procesul de comprimare de referinta. La comprimarea fara aport de caldura, comprimarea se face adiabatic. Aceasta va conduce la randamentul adiabatic.
In loc de puteri se poate trece la sarcini (H) si la lucrul mecanic (L).
Pentru 1 kg de agent se poate scrie:
li=la-Km
Pi=m-li
K i=lu
li
Ventilatoare, suflante, turbocompresoare
3.4.1.2. Randamentul adiabatic
La comprimarea fara racire artificiala, procesul de comprimare este comparat cu cel adiabatic real (reversibil), la care lucrul mecanic este:
l
ad
|
T p1 |
Had cpT1
k-1
Kp1J
[J / kg]
La comprimarea adiabatica reala (ireversibila) exista pierderi de lucru mecanic, datorita frecarilor agentul de lucru, care se transforma īn caldura si actioneaza asupra fluidului, īncalzindu-l. Ca urmare si temperatura finala (de refulare) va fi mai ridicata decat la procesul de comprimare adiabatica ideala.
Considerānd cele doua comprimari adiabatice, una ideala, cu puterea Pad, si o a doua cu adaus de caldura, datorita frecarilor agentului, cu puterea Padp, rezulta raportul, denumit randament adiabatic:
|
PL H ad ad |
|
ad |
|
K |
|
|
|
|
|
|
|
ad |
P adp L adp H adp
Pentru compresorul neracit lucru mecanic adiabatic cu pierderi, Ladp, este diferenta entalpiilor la iesirea si la intrarea īn masina:
ladp=i2-i1=cp(T2-T1l [J/kg]
si cu aceasta randamentul adiabatic devine:
k-
|
|
|
K |
|
|
|
ad |
Fig. 3.8 Procesul adiabatic ideal si real
p2
yp1u
T T1
k
Aceasta expresie reda randamentul adiabatic Kad īn functie de marimile de
stare p1, T1, T2 si raportul p1/p2 ale agentului de lucru.
Se observa ca expresia
randamentului adiabatic contine si pierderile de lucru mecanic īn procesul de comprimare adiabatica.
Aceste pierderi sunt numai o parte din pierderile interioare totale (nu exista schimb de caldura cu exteriorul).
Ventilatoare, suflante, turbocompresoare
Din figura se vede ca lucrul mecanic adiabatic, cu īncalzire (real), este dat de suprafata:
ladp=aria{c-2-3-a-b-c)
iar lucru mecanic ideal:
lad=aria{b-2ad-3-a-b) Diferenta celor doua lucruri mecanice o constituie pierderilor interioare totale:
Uad=ladp-lad=aria(c-2-2ad-b-c)
|
|
|
Mad=H adp-H ad=H ad |
, [J /kg]
\Vad J
Mad =cpdT = cp(T2 -T2ad), [J/kg]
Mad=i2-i2ad, [J/kg]
Utilizarea randamentului adiabatic reclama multa experienta practica. In acest caz lucrul mecanic efectiv, Ladp, comform diferentei, este acel lucru mecanic consumat la un compressor ideal (fara pierderi) īn cazul agentul termodinamic evolueaza īntre aceleasi stari de īnceput si sfārsit, ca si īn compresorul real.
3.4.1.3. Randamentul politropic
In figurule 3.9 si 3.10 este reprezentat procesul de comprimare īn trei trepte, īn diagramele p-v si T-s, neluānd īn considerare pierderile de presiune īntre trepte.
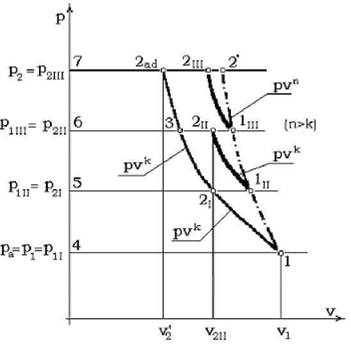
Fig. 3.9 Procesul de comprimare īn trei trepte īn diagrama p -v
Ventilatoare, suflante, turbocompresoare In diagrama p-v (fig.3.9) lucru total de comprimare adiabatica īn cazul comprimarii ideale īn trei trepte este reprezentat de suprafata (1-2'-7-4-1), iar a treptei īntāi de suprafata (1-2I-5-4-1). Lucrul mecanic adiabatic al treptei a doua este proportional cu suprafata (2I-3-6-5-2I) si al treptei a treia cu suprafata (3-2'-7-6-3), deci lucru mecanic adiabatic de comprimare totala al compresorului este proportional cu suma lucrurilor mecanice ale treptelor.
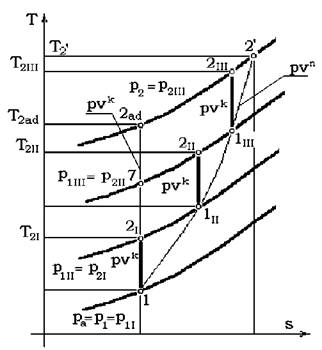
Fig. 3.10 Procesul de comprimare īn trei trepte īn diagrama T -s
In cazul real, cānd exista si pierderi, aceste suprafete nu sunt egale cu suprafetele amintite. Trepta a doua are o suprafata ceva mai mare (1II-2II-6-5-1II), la fel si a treia (1III-2"-7-6-1II). Aceasta din cauza ca volumele specifice sunt mai mari decāt īn cazul comprimarii adiabatice (fara pierderi), ca urmare a īncalzirii. Aceste suprafete diferite īntre ele (mai mari īn cazul comprimarii cu pierderi), duc la lucruri mecanice diferite pe fiecare treapta, ceea ce da ca rezultat ca lucru mecanic total pe compresor īn cazul comprimarii cu pierderi este mai mare decāt īn cazul comprimarii fara pierderi. Considerānd cazul comprimarii cu pierderi, conturul 1-2I-1II-2II-1III-2" si luānd un numar de z trepte destul de mare si unind īn diagramele p-V si T-s punctele de īnceput ale fiecarei trepte obtinem curba denumita "politropa''. In acest caz lucrul mecanic efectiv va fi suma lucrurilor mecanice adiabatice pe trepte:
lef Hef z,hadj
iar lucru mecanic interior se considera acum suma lucrurilor interioare pe trepte:
Ventilatoare, suflante, turbocompresoare
li Hi z hij
j 1
Daca had tinde spre zero, atunci z tinde spre infinit si īn acest caz lucru mecanic denumit politropic va fi proportinal cu suprafata (1-2-7-4-1) iar pierderile vor fi date de suprafata cuprinsa īntre adiabata (1-2') si politropa (1-2).
In acest caz raportul dintre lef si li va fi randamentul politropic:
|
l ef |
K
pol
lim z ha
|
|
|
lH |
adj
ef ef j 1
|
Hi |
lim z hij
j 1
cānd
z of
Pentru o treapta, din ecuatia de mai sus (152) se deduce randamentul adiabatic:
|
h ad .tr hi |
|
K |
|
|
|
ad .tr |
|
i.tr |
Aceasta randament depinde de n si de p2/p1 si este independent de ordinea treptelor. Aici s-a considerat ca transformarea adiabatica este un caz particular al transformarii generale politropice si ca Kpol este o valoare limita, catre care tinde Kad
cānd hadj tinde la zero.
Acest lucru poate fi aratat astfel:
pvn const.
sau:
n_1
T
const.
sau pentru punctele (1) si (2) ale politropiei se poate scrie:
n_1
n_1
|
T1 |
|
T2 |
p1 n p2n
sau:
n_1 p2n
de unde se poate deduce exponentul politropic n:
n_1
n
log
log
p2 p1
Aceasta expresie mai poate fi pusa si sub forma:
Ventilatoare, suflante, turbocompresoare
r
log1 +
k-
k
n-1 L
|
n |
log
Vp1;
In care exponentul politropic este functie de randamentul adiabatic si de raportul presiunilor p2/p1.
Spre exemplu, conform figurii anterioare, randamentul adiabatic al unei trepte poate fi pus sub forma:
K
ad .tr
p6 p5
T1
k-
k
T .II
In acest caz s-a ales o treapta oarecare, a doua, conform figurii 3.9 si 3.10 īn care p5 p1II p2 I si p6 pII p1III
Raportul presiunilor pe treapta este:
n
|
T 1.III |
n-1
T .
si cu aceasta randamentul pe treapta Kadtr este:
n k-
|
T 1.III |
|
h |
|
T1 |
|
yT ii j |
n-1 k
|
K |
|
ad ..tr |
|
|
|
|
|
ad .tr |
|
T1 |
|
hi |
|
i.tr |
1.III
T 1.II-1 Daca hadtr tinde la zero atunci raportul T1 III /T1 .II tinde spre 1 si expresia de mai
sus ia o forma nedeterminata 0/0. Pentru ridicarea nedeterminarii se diferentiaza atāt
numaratorul cāt si numitorul īn raport cu T1III/T1.II si se obtine:
|
n |
x±_
|
I1 III V T1-II J |
x n-
|
lim |
|
K |
|
|
|
|
|
T1 T1 |
|
ad .tr |
_x-1n x "n-1
|
1III |
1II
Se vede ca randamentul adiabatic al treptei elmentare Kadtr depinde numai de exponentul politropic n, care la rāndul lui depinde de p2II/p1II . Din aceasta cauza
Ventilatoare, suflante, turbocompresoare
politropa corespunde unei comprimari cu un randament constant pe treapta. Cu aceasta:
|
|
IX. j had. j
|
h ij |
Thij
si de aici rezulta:
|
h K lim adj K pol ad.tr h ij |
Aceasta expresie arata ca randamentul politropic Kpol este identic cu randamentul adiabatic al treptei elementare Kad .tr
Randamentul politropic mai poate fi pus si sub forma:
K
|
x |
pol
|
|
|
|
x_1 g p1x-1 n
|
T2 T1 |
|
x |
|
log |
n-1
Pe īntreg procesul de comprimare K
pol
>Kad
Dependenta īntre cele doua randamente se obtine din:
T2
x-1
pO x
de unde, conform relatiei de mai sus, se obtine randamentul politropic:
|
log |
|
|
log
|
K |
|
ad |
x-1
x
11
|
p1 |
V p1 /
Rezolvānd aceasta ecuatie īn raport cu Kad se obtine:
x-1
|
ad |
Ka
x
p1J
x-1
x K
p1J
pol
Randamentul adiabatic, īn general, se masoara si chiar se calculeaza cu el, īn cazul compresoarelor frigorifice, dar se recomanda ca sa se utilizeze randamentul politropic , fiind mai precis.
Ventilatoare, suflante, turbocompresoare
Calitatea unui turbocompresor este caracterizata de fapt prin randament treptei, deci prin randamentul politropic.
Desi randamentele treptelor sunt egale īntre ele, totusi randamentul adiabatic total pe compressor este cu atāt mai mic cu cāt raportul presiunilor este mai mare.
3.4.1.4. Pierderi prin īncalzire
In cazul turbocompresoarelor neracite, comprimarea adiabatica īn mai multe trepte aduce un surplus de lucru mecanic fata de cazul comprimarii adiabatice īntr-o trepta īntre aceleasi presiuni p1 si p2 . Diferenta va fi:
Al = z had~Had
j=1
Conform fig. 3.9, aceasta diferenta este reprezentata de suprafata (1II -2II -1III-2''-2''-2II -1II). Aceasta suprafata este marginita de curbele adiabatice al treptelor, care sunt transformari de stare reversibile. In cazul cānd numarul treptelor tinde spre infinit, atunci pierderile totale vor fi reprezentate de suprafata (1-2-2 -1) numita pierdere prin īncalzire. Aceste pierderi sunt cauzate de marimea volumului specific a gazului, ca urmare a īncalzirii prin frecare. In cazul comprimarii politropice aceasta difereta poate fi pusa sub forma generala:
Al f fJhadj-Had «suprafata 1-2 -2'-1
j=1
Pentru a usura īntelegerea fenomenului se defineste un '' factor de pierdere prin caldura'' f sub forma:
Al
|
j=1 |
f = 1 sau l + f=^
H ad H ad H ad
pentru cazul a z trepte (finit), si:
|
|
H ad
pentru cazul cānd numarul treptelor este infinit (politropic). Prin īnmultirea numaratorului si numitorului cu 1/Hi expresia 173 devine:
l + i f H = K
ad K ad
Ventilatoare, suflante, turbocompresoare
cu ajutorul ecuatiei (169) aceasta ultima relatie devine:
l + f f K por
p2 p1
1 x-1
pol
x-
x
vp1J
Considerānd ca īn diagrama T-s (fig. 3.10) triunghiul format de laturile (1-2), (2-2), (1-2) poate fi exprimat prin numarul de z trepte - si anume: o latura a unui triunghi mic, a unei trepte, poate fi exprimata prin 1/z ori din latura triunghiului 122', iar suprafata de 1z2 din acelasi triunghi 122'.
Considerānd ca exista z triunghiuri mici, suprafata care reprezinta pierderile prin īncalzire va fi de (1-z/z2)- (1-1z) ori din suprafata īn cazul celor z trepte va fi:
f = f f
z Din ecuatia (172), prin īnmultirea cu 1/Hi se obtine:
|
adj |
|
H ad Hi |
l+f=j"
sau:
|
K |
l + f =
treapta
|
ad |
K
Tinānd seama de ecuatiile (176) si (174) se poate deduce :
|
K |
|
z |
|
z |
|
pol |
|
|
|
|
|
K |
|
VK ad |
f ff
si cu ajutorul ecuatiei (178) se obtine:
|
f K zj |
|
K ad |
|
|
|
K ad |
K
teapta
pol
In general la un compressor care se īncearca pe standul de probe se pot masura conditiile initiale de aspiratie {p1,T1) si de cele de refulare (p2,T2), apoi conform ecuatiei (146) si (147) se poate calcula Kad,conform ecuatiei (166) Kpol iar conform
ecuatiei (180) Ktreapta.
Ventilatoare, suflante, turbocompresoare
Pentru usurinta calcului s-au trasat cāteva diagrame ca Kad si ff īn functie de
pil pi.
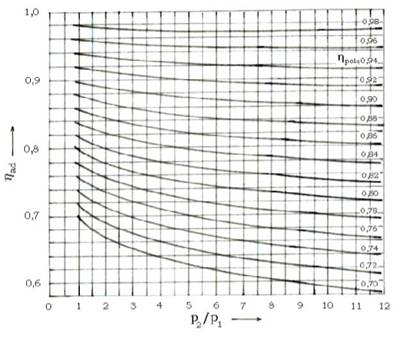
Fig. 3.11 Dependenta dintre randamentul adiabatic si politropic īn func tie de raportul de
comprimare (pentru aer k
|
|
|
Fig. Pierderile prin īncalzire ff īn functie de raportul de comprimare |
|
|
Randamentul treptei rezulta ca randamentul adiabatic pentru un randament politropic ales, īn conditii de presiune ale treptei.
Ventilatoare, suflante, turbocompresoare
3.4.2. Turbocompresorul racit 3.4.2.1. Generalitati asupra racirii turbocompresoarelor
Se cunoaste faptul ca pentru conprimarea izotermica se cheltuieste mai putin lucru mecanic decāt pentru comprimare adiabatica. Pentru realizarea comprimarii izotermice este necesar ca toata caldura produsa īn timpul comprimarii sa fie evacuate. La turbocopresoare, aceasta caldura se produce aproape īn īntregime īn rotorii compresorului si poate fi evacuata prin diferite mijloace.
Daca evacuarea caldurii de comprimare se face dupa fiecare rotor īn parte, īn statorii compresoarelor, atunci se spune ca este o racire interioara, iar daca racirea se petrece īn aparate separate, īn afara compresoarelor, se numeste racire interioara. Agentul de racire, īn general, este apa.
Racirea interioara se petrece īntre iesirea din rotor si intrarea īn rotorul urmator, prin suprafetele de schimb de caldura ale statorului. Constructia este complicata si scumpa. Spatiile de racire trebuiesc prevazute cu orificii de vizitare si de curatire, deoarece apa depune piatra pe peretii canalelor.
Racirea exterioara este mai simpla din punct de vedere al constructie compresorului, īnsa necesita schimbatoare de caldura separate. La aceasta racire trebuie avut īn vedere si pierderile de presiune suplimentare date de aceste schimbatoare de caldura denumite si racitoare intermediare sau finale.
3.4.2.2. Racirea exterioara-intermediara fara pierderi de presiune
In general, racirea se aplica numai la compresoarele radiale si īn rare cazuri la compresoare axiale. La compresoarele radiale se aplica o racire combinata interioara si exterioara. Acest sistem da maxim de eficienta cu cheltuieli minime. Intr-adevar īn acest caz, al racirii combinate, compresorul se executa cu spatii de racire cāt mai simple, iar racitoarele exterioare cāt mai mici. Racirea interioara depinde de spatiile de racire, adica suprafetele de schimb de caldura, sunt limitate constructiv si deci si de racirea gazului este limitata. Din aceste motive racirea se face oricānd de mult īn racitoarele intermediare si trebuie sa i se acorde o atentie deosebita.
Spre a usura expunerea acestei probleme se considera cazul comprimarii īn trei trepte, fara a tine seama de pierderile de presiune din racitoare.
Ventilatoare, suflante, turbocompresoare
Fig. 3.16 Procesul de comprimare īntr -o turbomasina cu trei trepte, cu r acire si fara racire īn
diagrama dinamica
In diagramele p-v si T-s (fig. 3.16 si 3.17), s-au trasat curbele pentru compresorul īn trei trepte neracite - liniile punctate si racit - linii pline.
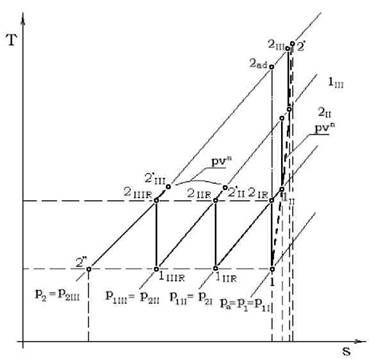
Fig. 3.17 Procesul de comprimare īntr-o turbomasina cu trei trepte, cu r acire si fara racire īn
diagrama calorica
Ventilatoare, suflante, turbocompresoare
Punctele 2ad, 2' si 2'' corespund comprimarii adiabate, izoterme si politrope īn cazul īn care s-ar utiliza comprimarea numai īntr-o singura treapta. Punctele 2'I I si
III corespund comprimarii politrope īn cazul compresorului racit.
Din diagramele de mai sus, se vede ca īn cazul comprimarii adiabate īn trei trepte racite, fata de comprimarea adiabata īn trei trepte corespunde lucru mecanic mai mare, reprezentat de suprafata 1II -2IIad -1III -2IIIad -2IIIR -1IIIR -2IIR -1IIR -1II .
|
|
Fig. 3.18 Schema turbomasinii ner acite, īn trei trepte
|
|
Fig. 3.19 Schema turbomasinii racite, īn trei trepte
Considerānd lucrul mecanic teoretic īn cazul comprimarii adiabate īn trei trepte racite fara pierdere de presiune cu lR0 si randamentele treptelor cu Kad I Kad II si Kad III se poate scrie relatia:
|
h |
|
K |
lR0
ad I
ad I
ad II
ad II
ad III
ad III
K
ad I
k
k-1
|
1II |
R-T1
|
2I |
p
|
p1 |
v p1II j
k-
k
|
p |
|
p |
K
ad II
k
k-1
|
1II |
R-T1
2 II
|
p |
V p1II J
k-
k
K
ad III
k
k-1
|
1III |
R-T1
2 III
|
p1 |
V p1III J
k-
k
[J / kg]
Ventilatoare, suflante, turbocompresoare
sau pentru un numar n de raciri dorite, expresia se poate restrānge īn forma:
|
2j |
lRW j 1 K a djk_1
|
1j |
R-T1
k
k
dar:
had j k
|
T1 |
|
1j |
k_1
|
p |
R
p
2j
v 1j 7
k_1
si ecuatia (182) devine:
l
R0
n
z
j 1
|
T 1j |
TIjJ
K
ad j
,[J/kg]
Considerānd ca temperatura T1j de intrare īn treptele compresorului este o temperatura medie T1m (racirea se face pāna la T1 aproximativ) expresia lucrului mecanic poate fi pusa sub forma:
l
R0
T1m n
j 1
Tl J
j
K
ad j
din ecuatia (183) si (184) rezulta:
|
z j 1 |
|
T1j |
|
K |
|
j |
|
1m |
T1
|
z j 1 |
(had
j
T1J
|
K |
ad j
ad j
Considerānd ca
(had
j
K
adj
este acelasi pentru toate treptele rezulta:
n T1j
|
|
T1m j 1 n
Acesta expresie este destul de exacta atāta timp cāt randamentele treptelor si temperaturile de intrare nu difera prea mult.
Se observa ca linia frānta din diagrama T-s tinde catre un proces izoterm, īn cazul cānd n of deci T1 j tinde spre T1m In acest caz sarcina treptei tinde catre zero,
iar randamentul devine Kpol Lucru mecanic fara frecare cānd nof devine
l
|
K |
Rf
|
R.T1m-in |
p2
L 1m p
iz
|
pol |
|
pol |
K
Ventilatoare, suflante, turbocompresoare
Aceasta valoare a lucrului mecanic trebuie sa fie comparata cu lucru mecanic de comprimare fara racire pentru raportul total de comprimare, adica:
Kad k-1
R-T1
k-
K ad
si facānd raportul:
|
|
|
l Rf |
|
k |
|
T1 |
|
Ka |
ln
pi) p)
p2 p1
k-
k
Fig. Variatia lui T īn functie de raportul de comprimare Introducānd expresia lui
Kad din relatia rezulta
|
k- |
|
p |
|
k |
|
kKp |
l
RfO
|
o |
l
|
1m |
T1
T1
vp1;
|
|
k±
pA
K
pol
k-1 ^p1
|
k |
|
p2 |
|
p1 |
pk
j
= T1m.kz1.
|
k |
T1
p
vp1u
|
p2 p1 |
|
T1 |
ln
k11 1=m=T
kKp
|
pol |
K
sau:
Ventilatoare, suflante, turbocompresoare
Valoarea T se da īn functie de p2/p1 , la diferite valori ale lui Kad respectiv ale lui
T
T
lT
o 1m
Kpol. Aceasta relatie este reprezentata īn diagrame de forma celor din figurile 3.20 si
Aceaste diagrame pot fi utilizate nu numai pentru evaluarea randamentului total al compresorului ci si pentru o grupa de trepte. Se vede imediat cāstigul de lucru fata de compresoarele neracite.
3.4.2.3. Pierderile de presiune prin racire
Pierderile de presiune prin racire cuprind nu numai pierderile de presiune īn racitoarele proprii (racire exterioara) ci si toate pierderile de presiune care se produc prin īnscrierea locurilor de racire īn compresor (racire interioara).
La racirea exterioara este necesar ca viteza gazului de lucru sa fie marita la iesirea din rotor si īn difuzor, pentru a putea īnvinge rezistentele la conducte pāna la si de la racitor la treapta urmatoare. La racirea interioara aceasta crestere nu este ceruta, deoarece caile de curgere a gazului sunt mult mai scurte. Pierderea de presiune īn racitor este definita ca o diferenta de presiune īntre presiunea totala de intrare īn trepta urmatoare dupa racitor si presiunea de racire din treapta anterioara a racitorului, indiferent daca exista sau nu si racirea interioara.
Considerānd aceasta cadere de presiune Ap fata de presiunea totala p , a treptei
anterioare racitorului, adica Ap/p , se vede ca aceasta pierdere influenteaza raportul
de presiune a treptei anterioare.
Daca nu ar fi racitor intermediar, presiunea de iesirea din treapta anterioara ar fi egala cu presiunea de intrare īn treapta urmatoare, lucru care nu mai poate exista īn cazul racitoarelor intermediare, deoarece raportul p2j/p1j trebuie marit cu factorul
p Astfel lucru de comprimare adiabata se mareste cu:
Ventilatoare, suflante, turbocompresoare
|
|
|
RT1 |
|
1j |
k-1
k
|
1j |
R-T1
k~1
k
p
2j
p
1j
k-
k
|
p 2j |
k-1
p2 k
|
p |
V p1j J
k-1
k
Kp1jJ
p
k-
k
Aceasta relatie reda nu numai raportul lucrurilor mecanice adiabate, dar si a lucrurilor mecanice reale, deoarece randamentul Kad este acelasi.
Aici ^« p
p2
vp1Jj
, asa ca expresia de mai sus poate fi considerata ca fiind
constituita din doua parti:
k-1
k
p
vp1J
j
p2) p1)
k-1
k
j
f
vp1jj
iar:
k-1
k
1=f
j
Considerānd pe Ap/p < 0.5, se poate scrie:
1 p
k-
k
Ap
kp
si cu aceasta se poate calcula lR/lR0 .
La calculul puterii unui compresor cu ire intermediara si cu pierderi de presiune se considera la īnceput procesul fara pierderi si dupa aceea cu pierderide presiune, obtināndu-se īn acest fel factorul Ap/p , care corecteaza primul proces. In general ca valoare medie se poate lua Ap/p « 0.03 .
Ventilatoare, suflante, turbocompresoare
4. TURBOCOMPRESORUL AXIAL 4.1. Introducere
Datorita studiilor teoretice date de aerodinamica, de teoria aripilor portante ca si a cercetarilor experimentale, compresorul axial a putut depasi stadiul de ramānere īn urma fata de compresorul radial. Actualmente compresoarele axiale au depasit mult pe cele radiale prin randamentul mai ridicat si prin cerinte de a transporta debite de gaz din ce īn ce mai mari.
|
|
Posibilitatile
de a atinge un anumit
raport de comprimare prin aranjarea mai
multor trepte, sunt mult mai mari ca la
compresoarele radiale. In plus spatial
ocupat este mult mai mic, iar turatiile
compresoarelor axiale, datorita
diametrului mic al rotorilor se pot ridica la valori mari.
De aici rezulta economie de
material si deci un pret de cost mai redus
decāt la cele radiale. Facānd unele
consideratii de ordin tehnico -e conomic
asupra celor doua tipuri de compresoare -
|
Fig. 4.1 Comparatie īntre preturile (masele) turbomasnilor radiale si axiale |
axial si radial si anume īn ceea ce priveste
compararea rapoartelor maselor si a
preturilor īn functie de debite a reiesit
fig.4.1.
Domeniile īn care lucreaza aceste compresoare sunt foarte variate, de la simple
ventilatoare industriale, la suflante axiale, pentru tunele, galerii de mina si la
compresoare axiale propriu - zise, pentru diferite scopuri.
Pentru obtinerea presiunilor ridicate (5 bari) se cupleaza īn serie pe acelasi ax mai multi rotori (mai multe trepte) iar pentru debite mari se cupleaza mai multe compresoare īn paralel.
Debitele pentru scopuri industriale īncep cu 104 m3/min iar presiunile cu 0,1 bari pāna la 5 bari.
4.2 Procesul de curgere īn compresorul axial In principiu un compresor axial se compune dintr-unul sau mai multe rotoare cu palete, de regula elicoidale, fixate pe acelasi ax. Intre aceste palete mobile ale roto-
Ventilatoare, suflante, turbocompresoare rului se intercaleaza coroane de palete directoare si palete redresoare (aparate de ghidare ) fixate pe carcasa compresorului, formānd statorul. Primul rānd de palete al rotorului este precedat de un rānd de palete directoare fixate pe carcasa statorului si au rolul de a imprima gazului o directie perpendiculara pe directia de miscare a rotorului. Paletele redresoare servesc pentru a redresa curentul de gaz rotitor, care iese din paletele rotorului. Un rānd de palete ale rotorului (o coroana a statorului) formeaza o treapta a compresorului.
Pentru simplificare se considera un compressor axial format dintr-o singura treapta (cazul ventilatorului).
La compresorul axial gazul intra axial īn compresor cu o viteza vm - viteza
meridiana, neglijānd componenta radiala ce s-ar putea creea, īn prima aproximatie curentul de gaz se deplaseaza elicoidal pe suprafata unui cilindru coaxial cu axul rotorului. Aceasta curgere corespunde unei curgeri plane printr-o retea cu un numar infinit de palete. O masa elementara de gaz patrunde spre rotor cu viteza vm si īn
contact cu acesta se deplaseaza cu viteza relativa w1 . In rotor deplasarea se face dupa o spirala pe suprafata unui cilindru imaginar si masa elementara iese cu viteza relative w2 (deplasarea este intārziata).
Compunerea vectoriala a vitezelor u si w2 da viteza absoluta v1 . Aceasta viteza v1 īn aparatul redresor urmator este micsorata pāna ce masa elementara paraseste aceasta paleta redresoare cu viteza absoluta v2 .
Viteza absoluta de intrare īntr-o treapta nu-i neaparata nevoie sa fie axiala. Gazul poate sa curga prin rotor cu o oarecare turbionare (rasucire), cazul plasarii unui aparat director īn fata.
Procesul de curgere īn rotor si īn aparatul redresor poate fi urmarit cu ajutorul triunghiurilor vitezelor. In figura s-a luat cazul unui compresor axial prevazut cu aparat director la intrare, rotor si aparat redresor.
Aici va trebui luat īn considerare, la rapoarte mai mari de comprimare, faptul ca viteza meridiana vm sufera o micsorare notata cu vm .
Cele trei triunghuiri ale vitezelor īn cele trei sectoare diferite ale compresorului axial (aparat director, rotor, aparat redresor) pot fi combinate īn asa fel īncāt sa apara o singura figura a desenelor pe treapta.
In cazul compresorului cu mai multe trepte reprezentarea vitezelor se face pe fiecare treapta si apoi triunghuirile vitezelor, diferitelor trepte, se suprapun īntr-o singura figura.
Intersectānd coroana rotorului cu un cilindru de raza r, si desfasurānd sectiunile paletelor pe un plan se obtine o retea de palete (numar infinit) (fig. 4.6).
Ventilatoare, suflante, turbocompresoare
Curgerea gazului prin masina se face prin linii de curent paralele cu axa rotorului, studiul curgerii printr-o retea este valabil pentru orice valoare a razei cilindrului cu care s-a imaginat sectiunea.
|
|
|
Fig. 4.3 Triunghiul vitezelor pentru o treapt a |
Fig. 4.2 Curgerea printr-o treapta axiala
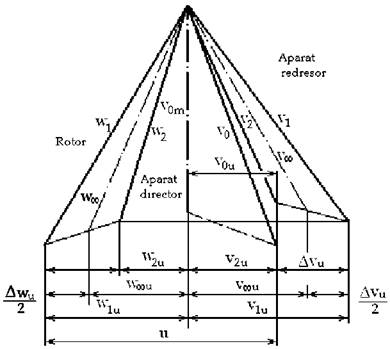
Reprezentarea vitezelor la un ventilator axial
Ventilatoare, suflante, turbocompresoare
Pentru examinarea procesului de curgere a gazului prin masina se va īncepe cu considerentul ca reteaua sa fie mobila la fel ca si gazul. In acest caz, se va considera numarul paletelor infinit (paletele foarte apropiate) si gazul ideal.
4.3. Ecuatia principala de dimensionare a compresorului axial
Considerānd ca o retea mobila de palete este plasata īntr-un curent de gaz, directia acestuia se va schimba, iar īn palete vor apare niste reactiuni ca urmare a presiunii exercitate de gaz asupra lor.
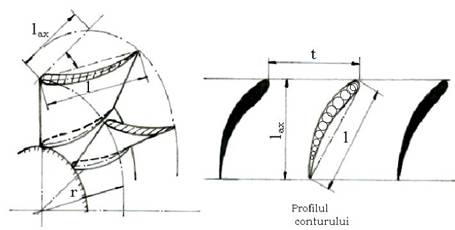
|
Fig.1 Fortele care apar īntr-o retea mobila la trecerea unui fluid f ara frecare |
|
|
Retea de palete axiala La o distanta astfel aleasa ca influenta retelei sa nu se exercite, se considera doua linii de current BC si DE, distantate cu pasul t.
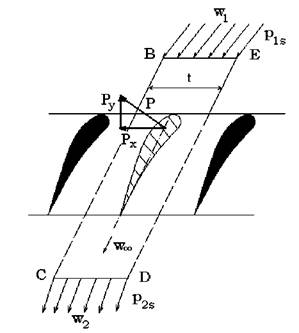
Ventilatoare, suflante, turbocompresoare
In starea destul de departe, īnainte de retea, exista presiunea statica p1s iar īn starea destul de departe, dupa retea, presiunea statica p2s
Conform ecuatiei lui Bernoulli, pentru un curent de gaz incompresibil, se poate scrie:
ptot=ps + U w 2
unde : ptot - presiunea totala a curentului; U - densitatea gazului;
w - viteza relativa a gazului īn raport cu gratarul mobil; Pentru cele doua pozitii rezulta:
w
w
sau:
p 2s=p tot~
w
w2 Diferenta de presiune īntre pozitia 1 si 2 este:
Aps=p2s-p1s=U(w -w22)
Asa cum s-a amintit, procesul fiind considerat pentru un gaz incompresibil, rezulta pentru viteza meridiana:
Triunghiul de viteze va fi īn conformitate cu figura 4.8: Conform figurii 4.8 rezulta:
Deci:
Aps=U(w u-w u)
Aceasta diferenta de presiune dintre starea 1 si starea 2 produce o forta de presiune a curentului de gaz asupra retelei mobile. Aceasta forta de presiune notata
Ventilatoare, suflante, turbocompresoare
cu P exercitata de gaz asupra retelei mobile poate fi considerata ca rezultanta a doua componente: una axiala Py paralela cu axa rotorului si alta Px - dupa axa retelei. Componenta Py poate fi dedusa din relatia:
|
1u |
|
|
|
|
Py =bt U{w21u -w22u)=btU1u w 2u{w1
w2J
|
|
dar:
|
-w2u-Awu |
|
si w1 |
|
w f u |
|
1u |
w 1u+w 2u
unde t este pasul, iar b este īnaltimea
paletei.
Deci:
Py=b-t-U-wfu-Awu
Componenta Px este chiar forta tangentiala T, care conform legii impulsului este:
Px=T = mAwu
m - este masa de gaz care se scurge īntr-o secunda prin sectiunea t-b, deci: m = U tbvm
|
Fig.4.8 Triunghiul vitezelor la curgerea f ara frecare |
Diferenta de viteza Awu īn directia axei gratarului pentru doua puncte departate de gratar este:
Awu=w1u-w2u
Forta tangentiala va fi:
Px=T = Utbvm(w1u-w2u) = UtbvmLw
Forta de presiune P va fi:
P = Px2^Py2 J(U tbvmAwu )2 + {btU wf uAwu U tbAwuwf
Facānd rapoartele lor, se obtine :
|
|
P
P wf
Ventilatoare, suflante, turbocompresoare
Din aceste rapoarte se observa ca forta P este perpendiculara pe directia
w1+w2 determinata de unghiul E Acest unghi
determina o directie medie, care 2
reprezinta directia vitezei w1 respectiv w2 "la infinit", adica la distante mari de reteaua
de palete, unde influenta paletei nu se manifesta teoretic.
Valoarea acestui unghi este:
w 1u + w 2u
ctgE2f =Py =
Forta P, dedusa ca mai sus, are o valoare si o directie care sunt independente de numarul de palete sau forma lor.
Relatia (1) se poate exprima si īn alt mod daca se recurge la expresia "circulatiei" īn jurul fiecarui profil al retelei.
Tp=v2ut2-v1ut1
Deoarece la compresorul axial pasul este acelasi:
t2=t1=t iar
v2u ~ v1u = w1u ~ w2u = Awu
sau:
P = bUwf t-Awu
La aceasta expresie se pot stabili anumiti coeficienti ca si la aripile portante. Astfel se defineste coeficientul de circulatie:
Cr -
U lb
w f Relatia (2) este denumita relatia lui Kutta-Jukowski. Din ecuatiile (1'), si (2) rezulta ecuatia principala de dimensionare pentru compresoarele axiale:
Crl-2w
t wf
Realizarea presiunii īntr-o treapta: īn rotor si aparat redresor, este functie de viteza de intrare si de iesire.
Aptot=ApsR+ApsAR
Dar pentru rotor este valabila relatia:
ApsR P(w12_w2)=pwfuAwu
si pentru aparatul redresor:
Ventilatoare, suflante, turbocompresoare
Ap^Ufv12
-v
)=Uvf uAvu
dar:
Awu = Avu
si:
w f u=u
v
ou
vf u - vou +
Awu
|
u.vou.wu vou wuv |
|
|
|
|
Inlocuind īn (4) rezulta:
4ptot = U Aptot = UuAwu Inlocuind īn ecuatia (3) rezulta:
|
2Apt |
|
l = |
|
tot |
|
Cr |
t Uuwf
Marimea C* l/t este numita coeficient de īncarcare. In general pentru un rotor axial se considera o crestere constanta a presiunii totale īn lungul razei.
|
si presiunea realizata, este |
Deoarece īnsa atāt viteza relativa w f cāt si viteza periferica descresc de la vārful paletei spre butuc, rezulta:
|
C |
|
> |
C
|
virf |
butuc
Incarcarea rotorului sau a aparatului redresor; determinata īn general de regimul curgerii lānga butuc.
La curgerea reala, se va lua īn considerare si frecarea pe profil notata cu W, care actioneaza īn directia vitezei relative medii wf. Aceasta forta de frecare W va diminua forta Py devenind Pyr iar rezultanta P va deveni Pr.
Conform legii impulsului, forta tangentiala Px nu este influentata de aceasta frecare, deci:
Pr = Py 2r Px2
Componenta fortei Pr perpendiculara pe directia vitezei relative medii wf se numeste forta portanta A.
Raportul W/A - tgH este denumit coeficient de alunecare.
Prin analogie cu coeficientul de circulatie C* de la curgerea fara frecare, la curgerea reala se defineste asa numitul coeficient de portanta CA:
Ventilatoare, suflante, turbocompresoare
CA
A pd S
A
wf-l-b
unde:
pd presiunea dinamica; S - suprafata aripii [m2]; l - profunzimea aripii (coarda), [m]; b - deschiderea aripii (perpendiculara pe wf ), apoi coeficientul de rezistenta Cw:
CW=W W
[m];
Cu aceste valori fortele tangentiale T=Px, si Py vor fi:
Px = U tbvmAwu =AcosWf+W sin Wf Pyr^bAps =Asin Wf-WcosWf
De unde:
|
-CwcosWf) |
|
|
|
sin W f |
Ap Py = Ul w f 2(Ca
s tb 2tx
XsinWf-HcosWf^CA l-
t
|
|
Fig. 4.9 Fortele īntr-o retea de palete luānd īn considerare recarea pe palet a
Unghiul Wf este format din directia lui A si T=Px sau de wf cu perpendiculara gratarului.
Schimbarea de directie (devierea) poate fi pusa sub forma:
|
CWtgWf ) |
Aw =w fl(CA
|
|
|
Awu=CA-{1 + H-tgWf w f |
|
t Pentru |
u 2 t\
coeficientul de
se obtine pentru
|
CT |
īncarcare
curgerea cu frecare relatia analoaga:
2Awu 1
|
|
Ca~ =
t w f HtgWf
Aceasta relatie trebuie sa fie considerata principala īn conditiile retelei, ca un coeficient de īncarcare.
Ventilatoare, suflante, turbocompresoare
Deoarece H CA
factorul
1 + H-tgW
f
CA- =
1, iar expresia se reduce la:
2Awu
|
|
La un randament ridicat este posibil ca:
CA= C*# Pentru raportul de repartizare t/l se poate aproxima valoarea minima:
|
|
l/t t
Din relatiile de mai sus rezulta ca īn sectiunea din imediata vecinatate a butucului rotorului sau aparatului de redresare ca valori practice de proiectare, pentru factorul de īncarcare se pot lua:
l=1,5...2,5
|
Cr |
t
Cresterea presiunii pe treapta conform ecuatiei (? ) este functie de raportul de acoperire l/t de coeficientul de circulatie C*, de viteza periferica u si de viteza relativa medie wf
Raportul de acoperire l/t este limitat de de constructia gratarului, de viteza periferica, de preturbionarea admisa, de wf si de numarul Mach.
O marire a presiunii pe treapta peste limitele corespunzatoare nu este posibila decāt prin marirea coeficientul de circulatie.
Dar coeficientul de circulatie creste cu unghiul de atac D. Aceasta īnseamna ca C este limitat de acest unghi deoarece de la o anumita valoare (unghiul critic Dcr) firele de fluid se desprind de pe suprafata superioara formānd turbioane.
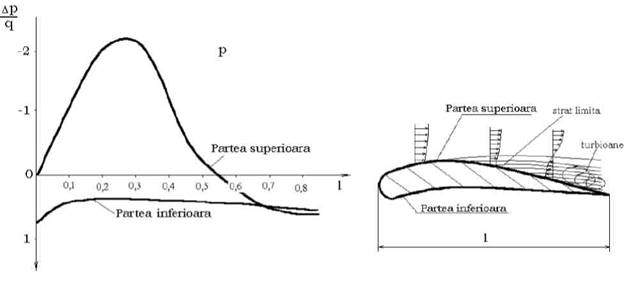
Fig. 4.10 Repartizarea presiunilor pe conturul unei aripi portante si curgerea pe partea
superioara a profilului
Ventilatoare, suflante, turbocompresoare
Pe suprafata profilului se formeaza un strat de fluid care adera la suprafata limita - si care la anumite valori ale circulatiei intra īn repaos sau chiar īncepe curgerea īn sens invers. In acest caz se zice ca s-a format zona de turbionare. Aceasta forma de curgere este caracterizata prin micsorarea fortei portante A si de cresterea rezistentei W.
Pentru a preīntāmpina aceasta forma de curgere se practica niste deschideri (taieturi) care pun īn legatura cele doua suprafete, cea superioara - de depresiune cu cea inferioara de presiune, pentru a crea o forta portanta mare, dar si o rezistenta mare.
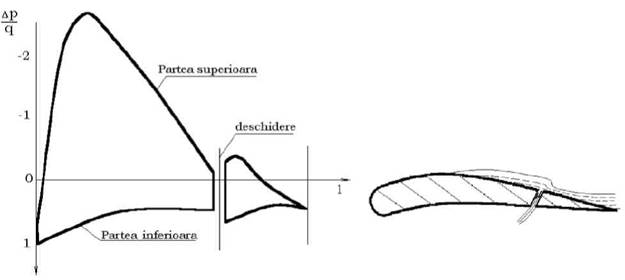
Fig. 4.11. Repartizarea presiunilor si formarea startului limit a pe un profil cu deschidere
Prin acest procedeu s-a activat curgerea pe partea superioara a paletei , prin accelerarea stratului limita. Trebuie amintit faptul ca formarea de turbioane - curgerea inversa se produce īn primul rānd la valori mari ale circulatiei C si mult mai mult, la profile fara deschideri īn aripi. Practicarea despicaturilor īn aripi duce la cresterea presiunii treptei.
4.4 Ecuatia diferentiala a curgerii īn compresorul axial
Pāna īn prezent s- a considerat curgerea prin coroana de profile numai pe un cilindru coaxial cu axa compresorului. Va trebui cerctat regimul curgerii si pe directie radiala, adica repartitia vitezelor si presiunilor īn sectiune transversala a compresorului. Trebuie amintit faptul ca si pentru acest studiu vor fi considerate, curgerea fara frecare, gaz incompresibil si ca miscarea se face pe un cilindru coaxial, deci fara componenta radiala.
In compresorul axial agentului termodinamic īi va fi imprimata o miscare īn directie periferica, prin paletele rotorului si ale aparatului director. Viteza absoluta v
Ventilatoare, suflante, turbocompresoare
este descompusa īn componenta axiala vm si īn componenta periferica vu . Componenta periferica produce forta centrifuga Fc . Pentru o masa elementara dm se poate scrie:
sau:
vu2
dFc dm
r
|
vu2 |
dFc=U.lr.dM-dr.u
|
|
|
īn care conform figurii 4.12: |
|
dm = U-l-r.dM-dr |
Fig. 4.12 Masa elementara īn rotatie
Aceasta forta este echilibrata de actiunea fortelor exterioare, de presiune, a caror rezultanta este:
dP = {p + dp)l-r.dM-p-l-r.dM dp-l-r.dM
Rezulta ca:
dFc = dP
Ventilatoare, suflante, turbocompresoare
sau:
dp = U vu2
dr r
Raportul - este gradientul presiunii statice īn lungul razei compresorului. dr
Cu ajutorul ecuatiei lui Bernoulli se scrie:
|
ptot=ps+U v2=ps+U(vm vu |
U v 2=p +
s 2
si cu aceasta ecuatia (228) se scrie:
|
dps d |
|
dptot dvm dvu |
|
dptot-U.v m dvm-U-v u dvu dr dr dr |
|
--vm2+vu2) |
|
|
p U(v2 dr dr
Prin introducerea ecuatiei (229) īn ecuatia (228) se obtine:
dr m dr u dr r
sau:
1dptot vm dvm vu vudv
U dr m dr \r dr Ecuatia (230) arata legatura īntre repartizarea presiunii totale si repartizarea vitezei īn lungul razei.
4.5. Influenta parametrilor asupra constructiei compresorului axial
Felul constructiv al masinilor de tip axial si sarcina lui sunt influentate de coeficientul de īncarcare al paletelor Cr, de actiunea echilibrului radial, de gadul de reactie k, de raportul diametrelor Q, de numerele Mach M si Reynolds Re.
4.5.1. Gradul de reactie
Consideram date viteza periferica u si devierea Aw īn gratarul de profile, atunci sarcina īntr-o treapta este aceeasi, oricare ar fi forma triunghiurilor de viteze. Stiind ca
repartizarea presiunii īn rotor de forma U(w2 -w2) este diferita de cea din aparatul
2\
redresor de forma - (v22-v12) se defineste gradul de reactie ca fiind raportul dintre presiunea statica creata īn rotor si presiunea totala a treptei, care se noteaza cu k:
Ventilatoare, suflante, turbocompresoare
k = ^pjL
Introducānd valorile presiunilor din rotor si a presiunii totale:
U
|
Aptot=U[(w12-w22)+(v2-v12)] = U.u.Awu |
ptot Ulw12-w22Klv22
īn relatia (1) se obtine:
k = w
In figura 4.13 se dau cāteva exemple caracteristice pentru triunghiurile de viteza īntr-o treapta cu aceeasi sarcina (Uu ■ Aw), dar cu grade de reactie diferite de la k<0 pāna la k>1 pentru structura: aparat director, rotor, aparat redresor.
In cazul w2>w1 nu exista o īncetinire a curentului si nici o ridicare de presiune, ci o accelerare deci o micsorare a presiunii statice īn rotor. Numaratorul ecuatiei (1) devine negativ deci k<0. Intreaga presiune a treptei se realizeaza īn aparatul director, respectiv redresor.
Pentru cazul cānd w2 = w1, deci w f u =0, k=0, toata presiunea se produce īn aparatul redresor
In cazul cānd k=0,5 triunghiurile vitezelor din rotor si aparatul redresor sunt simetrice, deci ridicarea presiunii se face atāt īn rotor cāt si īn aparatul redresor.
Daca valoarea coeficientului de reactie este k = 1, v2 = v1, toata presiunea se produce īn rotor.
Cazul k>0, invers cazului k<0, corespunde situatiei cānd toata presiunea se produce īn rotor.
Considerād expresia:
iSptot=U-u-Lwu
Se pot spune urmatoarele:
viteza periferica u ramāne aceeasi oricare ar fi gradul de reactie
vitezele medii w f si v f variaza cu gradul de reactie. Coeficientul de īncarcare
este direct dependent de gradul de reactie Cr - = - = fik). In cazul cānd w1 = w2, w f
t wf
se identifica cu vm, k=0, deci este mic. In acest caz coeficientul de īncarcare este foarte mare īn rotor, si mic īn stator.
De un deosebit interes se bucura cazul cu k=0,5 cānd w f v f , rotorul si statorul sunt egal īncarcate si la fel construite. Dar gradul de reactie este variabil de-a lungul razei rotorului (razei treptei).
Ventilatoare, suflante, turbocompresoare
|
|
Fig 1 Triunghiurile de viteze pentru o treapt a de masina axiala cu aceeasi sarcina dar cu grade de reactie diferite
Considerānd curgerea axiala la vārful paletei, gradul de reactie va fi:
|
uv-wuv |
|
w v fu |
|
|
|
u |
|
uv |
|
V u A |
kv
'wuv
2uv
iar la butuc:
|
ub~wub |
|
w b fu |
|
'wub |
|
kb |
|
|
|
|
|
u |
ub 2ub
Daca treapta masinii axiale va fi construita cu o crestere constanta a presiunii totale pe raza atunci:
V u j
Ventilatoare, suflante, turbocompresoare
ptot U uv wuv U ub wu uv wuv ub wub
sau:
|
wuv wub |
wuv
ub uv uvQ
unde:
db Q
dv db - diametrul butucului; de - diametrul exterior al rotorului si cu aceasta:
|
wuv 1 2uv Q |
kb =1_^wuv1
2uv Q De unde:
kb<kv
Din aceasta ultima relatie se vede ca gradul de reactie nu este constant de-a lungul razei, si nici īn lungul axei, treptele masinii axiale prin cuplarea aparatului redresor micsoreaza gradul de reactie.
4.5.2. Raportul diametrelor
Tendinta de a ridica cāt mai mult presiunea fluidului īn compresor conduce la un raport al diametrelor Q cāt se poate de mic. In apropierea butucului viteza periferica este mica, ca urmare si viteza relativa ww, este la fel de mica, din aceasta cauza este necesara o mare deviere a paletei pentru a se ajunge la presiunea ceruta.
Aceasta deviere a paletei este limitata de coeficientul de īncarcare Cr -. In prima
r t
aproximatie se poate lua:
Q
unde este coeficientul de presiune:
u 2
2 2
In afara de coeficientul de īncarcare Cr - trebuie tinut cont si de unghiul de atac D
care īn prima aproximatie se ia egal cu Ea. Apoi gradul de reactie k descreste spre butuc īn asa fel īncāt la un regim de curgere foarte īncet, sa devina mai mic ca zero.
Ventilatoare, suflante, turbocompresoare
Randamentul treptei este influentat foarte mult de cele aratate mai sus. Ca limita inferioara pentru Q se ia:
Q t
La valori ale lui Q īntre si se poate aproxima ca randamentul treptei sa fie egal cu randamentul adiabatic interior: Ktr Kiad
4.5.3. Numarul Mach
Presiunea obtinuta īn treapta compresorului ptot respectiv sarcina had se stie ca depind de coeficientul de presiune si, īn sfārsit, de viteza periferica a rotorului u
'ptot \, [N/m 2 ] respectiv:
De aici s-ar parea ca este recomandabil ca sa fie utilizata o turatie cāt mai mare, atāt cāt conditiile mecanice, de rezistenta si de echilibru permit. Dar o crestere a vitezei periferice ue, atrage si o marime a vitezei relative w1. Viteza relativa w1 īn acest
caz se apropie de viteza sunetului, iar coeficientul de rezistenta CW creste foarte repede īn timp ce coeficientul de portanta CA scade. Coeficientul de circulatie H CW/CA creste la fel foarte repede, ceea ce duce la micsorarea randamentului compresorului. Aceasta influenta a cresterii lui w1 la compresoarele axiale se traduce prin raportul dintre viteza relativa w1 (la intrare) si viteza sunetului a īn aceleasi conditii, denumit numarul Mach:
|
w1 a |
w1 M
unde:
a -JkRT1stat
este viteza sunetului.
Pentru aer, cu k =1,4, viteza sunetului este:
aaer 20.02^T1stat
Acelasi lucru se poate petrece īn aparatul redresor si īn aparatul director, deci curgerea este limitata de numarul Mach. Forma profilului influenteaza foarte mult
Ventilatoare, suflante, turbocompresoare
curgere. Profilele subtiri sunt recomandate pentru compresoarele axiale. Daca numarul Mach depaseste valoarea 0,85 atunci intervin perturbatiile amintite.
|
|
Se recomanda ca:
M≈ 0,75.0,80
dar fara ca aceste limite sa fie fixe.
Ca valoarea maxima pentru numarul Mach se considera acel raport w1a la care īn sectiunea cea mai īngusta īntre doua palate vecine se atinge viteza sunetului.
Considerānd un canal īntre cele doua palete de īnaltime radiala h = 1, si notānd doua sectiuni, una cu A1 īn afara
|
Fig. 4.14. Coeficientii profilului īn functie de numarul Mach |
gratarului unde viteza fluidului este w1 si
alta Amin unde viteza este w , la īnceputul canalului ghidat de cele doua palete conform figurii 4.15, se vede ca prin ambele sectiuni curge acelasi debit, dar īn sectiunea Amin trebuie sa se atinga viteza
sunetului.
|
|
|
w1 2cp |
|
Ttot =T1 + |
|
unde: |
|
T 1 = T 1stat si cp=R k-1 |
|
caldura specifica, īn sectiunea |
|
la presiune constanta, A . min Viteza de curgere a curentului poate fi pusa sub forma: |
|
Fig. 4.15. Reprezentarea sec tiunii de intrare A1 si Amin īntr-o retea |
Temperatura totala va fi:
w1=M1a=M1JkRT1
|
kr |
|
k 2R |
|
k-1 |
Ttot=T1 1 + M
T1
k-1
M12
Considerānd o curgere adiabatica īntre A1 si Amin (Ttot const.) se poate scrie:
Ventilatoare, suflante, turbocompresoare
|
tot |
|
min |
|
tot |
Ttot ( A) Ttot ( Amin ) Tt
|
A min |
Daca: MA 1, rezulta:
Ttot T
A
min
k-1
Din ecuatiile (242) si (243) rezulta:
T1
M12
T1
1 Facānd raportul vitezelor īn cele doua sectiuni si daca w
A
min
w* a se obtine:
A min
|
T |
|
w1 |
|
w1 |
M1kRT1
|
A min |
wA w ŢkRT
M1
T1
A
min
Prin cele doua sectiuni curge acelasi debit deci, se poate scrie:
Aw A w*
min
|
v1 |
v*
sau:
|
k- |
|
A min |
|
T1 |
|
V J |
|
|
|
|
|
k-1 |
|
T1 |
|
A1 w*v1 Introducānd relatia īn pentru M1 M1max se obtine: |
|
M |
|
VTAminJ |
A wv*
min
v1
|
T1 |
|
VTAmin 7 |
v
|
M |
|
|
|
A |
min
A1
-Mlmax
|
|
k-1
ml
si cu k =1,4, pentru aer:
|
1max J |
A
min
A1
M
1max
1 + 0,2M2
Aceasta expresie da legatura īntre numarul lui Mach M1 M1max si raportul
A sectiunilor min .
A1
Ventilatoare, suflante, turbocompresoare
Pe lānga numarul M1max mai exista si un numar Mach critic, caracterizat prin
aceea ca o supraviteza pe partea de aspiratie a profilului se produce cu viteza sunetului. Numarul Mach critic depinde de forma profilului, de unghiul de atac, de repartizarea vitezelor si presiunilor īn lungul suprafetei superioare. In mod obisnuit repartizarea presiunilor se pune sub forme:
q1 f( ' ) {U/2)
w
unde Ap reprezinta diferenta presiunilor statice īnainte de retea (p1) si a presiunilor pe suprafata superioara a profilului (p) iar q1 = ptot -p1 - reprezinta presiunea dinamica
|
U |
|
|
|
w |
a agentului de lucru cu viteza w1 . In cazul fluidului incompresibil q1
Daca īntr-un loc se obtine o supraviteza egala cu cea a sunetului, dar fara sa o depaseasca, repartizarea presiunilor se face, la curgerea compresibila, dupa regula lui Prandtl:
M1
|
p1 |
(aici indicele o arata lipsa pierderilor de presiune). In cazul compresibil:
|
|
|
T2Lk-1_1 |
k
|
|
|
|
|
|
|
tot |
|
T1 |
|
|
q1=ptot-p1 =
v
j
k
Depresiunea maxima īn punctele cu cea mai mare viteza este:
|
p |
|
k-1 |
|
min |
Apmax=p1-pmin =
|
p1 |
min
1 J
p1
|
T1 |
1_(T*
V 1 J
k
k-
r
p1
T tot T 1
V tot/Tmin J
daca īn locurile cu presiune minima s-a atins viteza sunetului, atunci:
|
Ttotk-1 |
|
T |
|
|
|
min |
si:
|
f |
r
pmax p1
L
|
M1 |
k-1
|
|
k
k-
Daca ecuatiile (248) si (250) la introducerea īn ecuatia (247) si M1 M1cr se obtine:
Ventilatoare, suflante, turbocompresoare
|
1cr |
max
|
q1 |
v q1 y
o
= 1-M2
|
|
1 k 1 M 2
1cr1
k-1
M2
1cr
k k-1
si pentru aer:
|
Apm |
|
Portanta unui profil se calculeaza īntr-o distributie eliptica: l U |
|
A^jApdx = b^max |
|
|
|
|
o
1-m c r
1 r1+0,2M1cr
|
|
|
f- |
M2 3,5 1cr
|
w |
|
|
calb
sau sub forma:
|
|
|
|
|
CA |
Apmax_2
U S
w1
Raportul w12 /wf īn domeniile obisnuite este de 1,1 pāna la 1,25 si atunci se poate scrie:
|
p |
|
q |
|
S |
|
opt |
V 1 J
In figura valorile lui CAopt sunt trecute pentru numerele Mach corespunzatoare. Orice alta repartizare decāt cea eliptica duce la diferente prea mari ale lui Apmax .
4.5.4. Numarul Reynolds
O alta marime care influenteaza si determina constructia si randamentul compresorului axial este raportul dintre fortele de inertie ale agentului de lucru si fortele de vāscozitate. Acest raport este cunoscut sub numele de numarul lui Reynolds si se noteaza cu Re.
La compresorul axial curgerea este totdeauna turbulents si rezistenta W se poate pune sub forma:
W = cw U w 2 S[N]
(S este suprafata paletei).
Ventilatoare, suflante, turbocompresoare
Aici CW este coeficientul de rezistenta la frecare si numai pentru curgerile care sunt mecanic si geometric, asemenea, are aceeasi valoare. El depinde de numarul Re:
Re w f
V
si de rugozitatea relativa l/k. unde:
wf [m/s] - viteza medie relativa īn rotor, respective vf īn aparatul redresor;
l [m] - o marime caracteristica a paletei;
v [m2/s]-vāscozitatea cinematica;
k [m] - īnaltimea rugozitatii;
l/k - rugozitatea relativa.
Din figura reiese ca la valori mari ale lui Re, coeficientul de rezistenta CW pentru o anumita rugozitate este constant, deci practic independent de Re. La valori mici ale lui Re, coeficientul CW depinde numai de Re si independent de l/k. Este fara īndoiala
ca la un compresor cu Re mic, suprafetele de trecere trebuie sa fie foarte fin prelucrate, deoarece ele se gasesc īn zona hidraulica neteda.
Numarul lui Reynolds influenteaza si randamentul treptei compresorului.
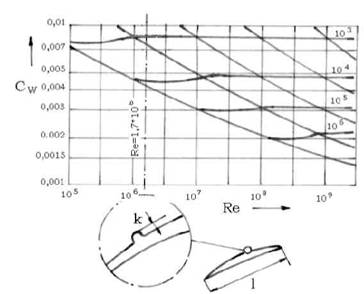
Fig. 4.17. Coeficientul CW īn functie de Re si l/k
4.5.5. Factorul de diminuare a puterii compresorului axial
Acest factor nu este o marime care sa influenteze felul constructiv al compresorului axial. In primul rānd acest factor depinde de raportul diametrelor v.
Ventilatoare, suflante, turbocompresoare
|
|
|
Fig. 4.18. Repartizarea vitezei meridiane īntr -o treapta a compresorului |
Pentru repartizarea componentei axiale a vitezei īn sectiunea transversala a compresorului, se considera o distributie constanta sau īn cel mai rau caz o repartitie corespunzatoare ecuatiei diferentiale a curgerii prin turbocompresor.
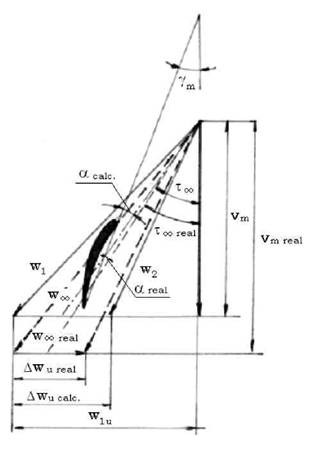
Fig. 4.19. Repartizarea viezelor meridiane pentru o sec tiune medie a paletei
Considerānd o repartizare constanta īn sectiunea transversala, din ecuatia de continuitate se poate calcula viteza meridiana vm
Ventilatoare, suflante, turbocompresoare
v----- ----- ---------- [m/s]
Dar curgerea reala este cu frecare. Vāscozitatea agentului de lucru, ca urmare a frecarii pe butuc, pe peretii carcasei introduce forta de rezistenta care trebuiesc luate īn considerare, īntrucāt coeficientul de circulatie, respectiv randamentul treptei vor fi influentate de acestea.
Actiunea vāscozitatii asupra agentului se manifesta prin aceea ca formeaza pe peretii de curgere un strat limita, care schimba profilul vitezelor īn lungul sectiunii transversale. Aceasta repartizare a vitezelor īn sectiunea transversala arata ca īn figura 4.18.
Scaderea vitezelor meridiane pe peretii compresorului fata de viteza medie favorizeaza īntoarcerea (curgerea īnapoi) a curentului pe coroana de palete. Acest lucru este aratat īn figura 4.19.
Din figura rezulta ca unghiul de atac Dreal < Dcalculat si factorul de circulatie:
Cr <Cr
real L calculat
Ca urmare si abaterea:
Aw ureal<Aw ucalculat
iar din ecuatia de contunuitate rezulta vmreal < vmcalculat dar numai la margini, pe butuc si peretii carcasei, deci:
h adreal<h ad
calculat
Aceasta micsorare a lui had se poate arata prin raportul:
n=h= Aw real = h^
h adcalc. w u calculat h calculat
Acest raport este numit factor de diminuare a puterii prin torsiunea curentului. Acest factor depinde īn primul rānd de raportul diametrelor si apoi de numarul Reynolds.
Considerānd coeficientul de presiune:
2Ha
cu had=u-Awureal ■ K treapta, [J/kg], rezulta sarcina reala:
had^.Awucalc.-Q-K treapta, [J/kg] cu coeficientul de presiune:
|
u |
e
Ventilatoare, suflante, turbocompresoare
si cu coeficientul de livrare:
M V----- ----- ------- 1=vm
-■d2(1-Q2)ue ue
eV
Coeficientul se face pornind de la relatiile:
K de unde h ad -h^K^,iar calc. ^
Coeficientul de īncarcare este aproximativ: Cr . = 1,5 y
r t
4.6. Calculul dimensiunilor principale ale compresoarelor axiale 4.6.1.Compresor axial īntr-o treapta cu diametrul exterior constant
|
|
Fig. 4.21. Valorile optime ale unei trepte
Numerele caracteristice īn acest caz sunt:
2Had
|
|
|
u |
|
e |
- coeficientul de presiune *F -
- coeficientul de debit M V = vm
A-ue ue
unde: Had - sarcina adiabatica [J/kg];
Ventilatoare, suflante, turbocompresoare
V - debit, [m3/s];
A - sectiunea compresorului la vārful paletei, A = d2 -Q2);
ue - viteza periferica la vārful paletei, [m/]s
Dintre aceste marimi cele mai importante sunt Had, debitul V si turatia n. Cu aceste valori se calculeaza coeficientul de rapiditate.
Q2
V 0,0351.n-
H 4 ad
Aceste patru ecuatii formeaza baza pentru dimensionarea compresoarelor axiale. Aceste valori sunt trecute īntr-o diagrama (fig.4.21) sub forma:
Mopt f1(V
opt f2 V
Qopt f3 V
Ktr.opt f4 V
4.6.2. Compresorul axial īn mai multe trepte In cazul compresorului īn mai multe trepte se utilizeaza diagrama din fig. 4.22.
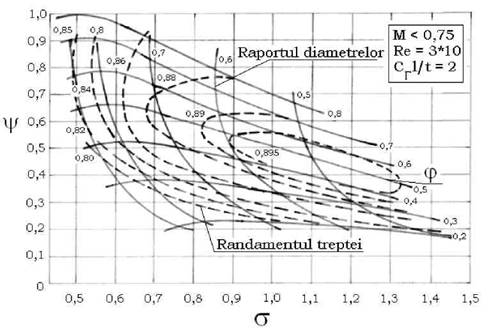
Fig. 4.22. Diagrama pentru compresoarele axiale, cu mai multe trepte
Avānd debitul V1 de la intrare si raportul presiunilor p2/p1 se poate calcula debitul de la iesire V2:
Ventilatoare, suflante, turbocompresoare
V
p2 p1
|
p |
|
K |
p2k
j
i ad
Randamentul adiabatic Kiadtrebuie aproximat la īnceput.Pentru compresoarele
axiale moderne cu had -105 y2-105 J/kg, K iadeste 0.83y0.88. Randamentele ridicate
corespund sarcinilor mici. Pentru aerul atmosferic este suficienta relatia debitului mediu:
|
|
|
Fig. 4.23. Dependenta raportului Had /'RT1 |
|
Sarcina adiabatica se calculeaza din datele cunoscute T1,k,R si p2/p1 : |
|
|
Ventilatoare, suflante, turbocompresoare
H
R-T1
p2
kp1u
k-
k
de unde:
|
ad |
H
RT1
k
k
care este reprezentata īn figura 4.23. īn functie de p2/p1 .
Cu acesta diagrama, la o turatie data, se poate determina coeficientul rapiditate al compresorului:
de
V
comp.
n-
Q2
|
H 4 |
ad
Cu acest coeficient t de rapiditate din fig. 2.4. se poate exprima numarul treptelor z ale compresorului axial.Cu aceasta valoare aproximativa a lui z se calculeaza sarcina unei trepte:
|
ha' |
ad treapta
|
ad |
H
z
, [J /kg]
Dupa aproximarea treptelor se determina factorul de īncalzire:
|
|
|
z |
f = f f
|
J |
V
f f se ia din relatia (175), sau pentru aer cu k = 1.4 , din diagrama din fig. 3.12. Cu aceste date se poate calcula sarcina medie pe trepta:
Had(1 + f)
|
z |
had.tr
Din relatia de calcul a coeficientului de rapiditate rezulta ca:din ce īn ce el devine mai mic (descreste de la treapta 1 pāna la treapta z). In schimb raportul diametrelor Q, ca si coeficientul de presiune, cresc, sau:
h dI <h ad.tr <h adz
hadI*(0,8...0,9)hadmed, iar pentru ultima treapta:
hadz«(1,1...1,2)had.med
Cu aceste valori hadI,VI ,n, se pot obtine valorile optime pentru coeficientul de presiune si de debit M apoi raportul diametrelor si randamentul treptei. Viteza periferica ue se obtine din ecuatia de definitie a lui
Ventilatoare, suflante, turbocompresoare
ue=
|
adI |
2h
I
Pentru viteza relativa la intrarea īn treapta, w1 e valabila relatia:
w12=v2m+(u-vJ=v2m+u2(1-C)2
|
v ou |
unde £ = este numit coeficient de preturbionare la vārful paletei:
u
|
|
M2 =
V a y
e
e
M 1_^j]
Cu acesta se va putea calcula preturbionarea pentru sectiunea exterioara:
u
ua
M
V a y
Marimea acestui raport depide de M .Considerānd aparatul director, din fata rotorului, care actioneaza ca o coroana de palete de accelerare, se va avea īn vedere ca nici un loc sa nu fie atinsa viteza sunetului.
In general valoarea lui £e max poate fi luata:
C.max*(0,45.......
Preturbionarea este limitata de aparatul director, deoarece aici se obtin cele mai mari devieri deci si cele mai mari viteze.
Diametrul exterior al primei trepte poate fi calculat cu relatia:
|
u 1e |
de=
V
(1-V2)M1-u
[m]
sau:
|
|
d =60.ue , [m]
S n
In cele mai multe cazuri diametrul exterior al compresorului, īn toate treptele este acelasi.
Pentru treptele compresorului este valabila relatia:
|
z> |
|
|
z ^2=ih=fa>f)
Daca diametrul exterior este constant, atunci ue2 /2 este acelasi si reltia devine:
z>
treapta
=uzhad=u Had(1+f)
Ventilatoare, suflante, turbocompresoare
Lungimea axiala a compresorului se poate calcula cu relatia:
|
l axial treapta |
la
y
de (valabila pāna la de y 600 , peste aceste valori, compresoarele devin mai scurte).
Ventilatoare, suflante, turbocompresoare
5. MASINILE DINAMICE DE TIP RADIAL (CENTRIFUGAL)
5.1. Generalitati
La masinile radiale ca si la cele axiale cresterea presiunii se obtine cu ajutorul fortelor pe care paletele, īn miscarea lor de rotatie, le exercita asupra agentului de lucru. Limita coeficientului de rapiditate la compresoarele radiale este cuprinsa īntre V
Fata de masinile axiale, cele radiale pot realiza un raport de comprimare, pe treapta, mai mare si deci o presiune mai ridicata.
Masinile radiale, la fel ca cele axiale au urmatoarele avantaje īn raport cu celelalte tipuri de compresoare:
capacitate si masa mai mica, conditionate de curgerea continua a curentului de agent de lucru si vitezelor mari de curgere prin sectiunile de trecere prin compresor;
functionare sigura si de lunga durata datorita uzurii foarte reduse;
echilibrare buna, lipsa fortei de inertie īn functionare;
uniformitatea debitarii agentuluide lucru, lipsa uleiului de ungere īn agent, si
posibilitatea cuplarii directe cu turbine sau alte motoare, ceea ce duce la un randament ridicat pe agregat.
Viteza periferica la masinile radiale de tip stationar este de 280.300 m/s, raportul de comprimare īntr-o treapta a aerului fiind de 1,6...18.
La masinile radiale de pe turboreactoare viteza periferica este de 450..500 m/s iar raportul de comprimare pe treapta, pentru aer este de 4,0..4,5.
5.3. Procesul de curgere īn masina radiala
In masina de tip radial agentul de lucru curge īn directie axiala īnainte de a intra īn rotor si apoi īn directie radiala prin rotor si difuzor.
Intre intrarea si iesirea din rotor, paletele acestuia transmit energia lor agentului de lucru conform legii impulsului, īn acelasi mod ca si la compresorul axial.
Viteza de curgere īnainte de intrarea īn rotor este v0 , paralela cu axa masinii,
iar la intrarea īn rotor devine viteza absoluta v1 care prin scaderea vectoriala cu viteza periferica u1 conduce la viteza relativa la intrare w1
Ventilatoare, suflante, turbocompresoare Dupa curgerea prin canalele rotorului, agentul de lucru paraseste rotorul cu
viteza relativa w2 , care prin adunare vectoriala cu viteza periferica u2 rezulta viteza absoluta v2 .
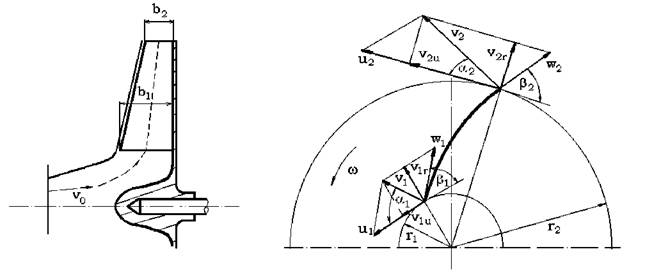
Fig.5.1. Triunghiurile vitezelor la intrarea si iesirea din rotor
u viteza periferica; v viteza absoluta; w viteza relativa; D unghiul de curgere;
E unghiul paletei; b latimea paletei; r raza
5.2.1. Dependenta sarcinii teoretice de directia de iesire a curentului din rotor (Influenta unghiului E2 asupra sarcinii teoretice Htf )
Unghiul E (unghiul de curgere) format de viteza relativa w1 cu viteza periferica u1 poate fi bine precizat si de regula, pentru rapoarte optime (p2/p1)opt se admite
E = 30o. Unghiul E2 (unghiul paletei) format de viteza relativa w2 cu viteza periferica u2 poate fi ales oricum. Ca urmare se vede clar ca numai unghiul de iesire E2 influenteaza sarcina teoretica a compresorului. Pentru a arata acest lucru se considera un rotor cu un numar infinit de palete, ceea ce presupune o curgere permanenta, conturul paletei se identifica cu īnsasi curgerea fluidului. Nu se considera frecarea agentului pe suprafata paletei. Se recurge la o figura īn care, pe un rotor, sunt trasate trei palete curbate, a caror unghiuri de iesire E2 sunt mai mici sau mai mari de 900.
In cazul cānd E2 < 900 curbura este īnapoi fata de rotatie, cānd E2 = 900 paleta este radiala la iesire si cānd E2 > 900 paleta este curbata īnainte. La intrarea agentului īn rotor, toate cele trei palete au intrarea radiala, adica v1u = 0 (fara preturbionare)
Ventilatoare, suflante, turbocompresoare
cum de regula este situatia īn cele mai multe cazuri si atunci sarcina totala teoretica va fi:
P-g g u2 g
sau:
v = g H
u2 u
Fig. 5.3. Triunghiurile de viteze pentru diferite valori ale lui E2
In aceasta relatie adimensionala se introduce coeficientul de presiune (coeficientul de sarcina) y/ conform definitiei:
Wf-
u2
si relatia(268) devine:
|
2u=*f u2 2 |
v2u Din triunghiul vitezelor rezulta:
tgE2 = v 2r
u2-v2u
Aproximānd v1r = v2r = vr si considerānd expresia:
a vl = v r
u2 u2
Ventilatoare, suflante, turbocompresoare
care poate fi considerata ca o marime ce caracterizeaza debitul, la intrarea īn rotor exista relatia:
v1r v1 u1tgE
apoi:
O u1 tgE 1=tgE 1
u2 d2
La fel la iesirea din rotor:
tgE vr1- O
u2
Aceasta relatie arata ca Htf si \f sunt date īn functie de O si E2.
5.2.2. Gradul de reactie
Raportul dintre presiunea statica, obtinuta īn rotor si sarcina totala a masinii se numeste grad de reactie:
H
kf sf
dar:
Hsf= - h22-u12)+{w12-w22\[m\ si considerānd intrarea radiala:
uv >@
|
tf g |
Htf 2u ,m
gradul de reactie devine:
2u2v2u
Plecānd de la ipoteza ca v1r v2r vr se pot scrie urmatoarele relatii:
w2-v2=(u2_v2J
-u -w =-(u2-vj
In acest caz gradul de reactie devine:
2u2v2u 2u2
sau:
Ventilatoare, suflante, turbocompresoare
kf=1-\f
In acest mod, ca si la definirea lui \f se poate stabili un coeficient de presiune numai pentru rotor:
\statf 2gHts f k f\f J \f \
|
J |
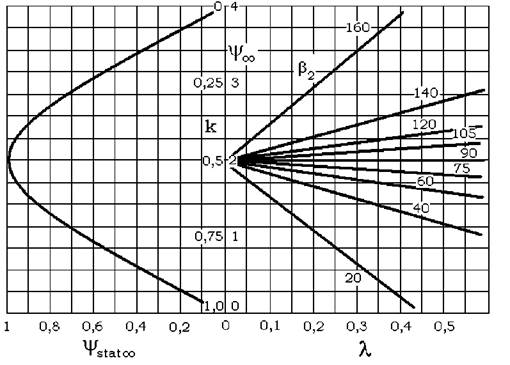
Fig. 5.4. Dependenta coeficientului de sarcina \f a gradului de reactie kf si a coeficientului de sarcina statica \sf de coeficientul O si de unghiul de iesire E2, īn cazul unui numar infinit
de palete
5.2.3. Alegerea unghiului E
Din figura 5.4 se vede ca odata cu cresterea unghiului E2 creste si coeficientul de presiune \f , la aceeasi viteza periferica u2 si la aceeasi sarcina Htf.
Gradul de reactie kf scade cu cresterea lui E2. Daca E2 > 900, coeficientul \f creste, dar gradul de reactie scade īn rotor.
La limita, cānd \f 4 si kf = 0 īn rotor nu se mai produce nici o crestere a presiunii statice, toata energia transmisa rotorului se transforma īn energie cinetica. O transformare ulterioara a acestei energii cinetice īn energie potentiala de presiune, īn difuzor, este destul de greoaie, se face cu pierderi destul de mari si nu se recomanda.
Ventilatoare, suflante, turbocompresoare
Acest tip de compresoare radiale, cu palete curbate īnainte, se utilizeaza la ventilarea spatiilor mari, unde nu se cere decāt o presiune mica dar viteze mari (debite mari).
In cazul unghiului E2 = 900, cānd k = 0,5, se obtine o transformare maxima a
energiei cinetice īn energie potentiala de presiune. In acest caz y/statf = 1 , iar
Htf = u22 2g . Din punct de vedere al rezistentei, paletele sunt moderat solicitate.
In cazul E2 < 900 se obtine totusi un randament foarte bun, cu toate ca alura caracteristicii nu este cea mai convenabila. Din cercetarile facute asupra acestor masini rezulta ca unghiul E2 are influenta si asupra puterii si asupra randamentului
adiabatic. Ca rezultat al acestor cercetari unghiul E2 variaza īntre 35 si 500. Cu micsorarea lui E2 scade y/f si Htf. Pentru cazul limita, cānd ff=0se obtine paleta "fara actiune" conform ecuatiei:
Valoarea minima a lui E2min este atunci cānd exista relatia r1r2 =1 (rotoarele Sirocco), adica E2min = E
5.3. Procesul de curgere īntr-un canal rotitor dintre doua palete
Procesul de curgere īntre doua palete s-a considerat ca fiind īn regim permanent, cu viteze relative constante pe toata sectiunea perpendiculara pe directia de curgere.
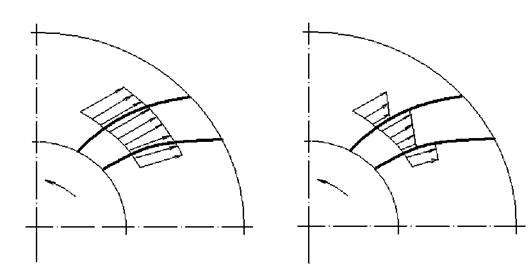
Fig. 5.5. Reprezentarea vitezelor relative īntr -un canal rotitor a - cazul ideal; b - cazul real fara a lua īn considerare frec arile
Ventilatoare, suflante, turbocompresoare
Din cauza miscarii relative (turbionare) care ia nastere īn canalul rotitor, vitezele relative īn sectiunea de curgere nu vor mai fi egale ci mai mari pe fata neactiva a paletei si mai mici pe fata activa a paletei. Energia preluata de fluid de la palete nu mai este distribuita uniform.
|
|
|
Fig. 5.6. Formarea misc arii relative rotitoare |
Miscarea relativa turbionara ce ia nastere īntr-un canal s-ar putea arata īn figura 5.6. Un canal din rotor este īnchis la ambele capete. Miscarea canalului se petrece cu viteza unghiulara Z In interiorul canalului ia nastere o miscare relativa de rotatie cu viteza unghiulara - Z īn jurul centrului de greutate al fluidului din canal. Eliberānd capetele canalului (se
deschid) miscarea relativa de rotatie din canal continua si vitezele relative de curgere ale fluidului se maresc pe fata neactiva a paletei si scad pe fata activa.
In cazul unui debit destul de mic, viteza curentului principal pe suprafata activa a paletei se poate reduce foarte mult, sub actiunea componentei inverse a curentului turbionar, devenind negativa, adica sa se petreaca o curgere inversa.
In cazul cānd debitul se micsoreaza si mai mult se poate īntāmpla o despindere a curentului de pe paleta.
5.3.1. Conditiile de echilibru ale curgerii relative
|
|
Fig. 5.7. Determinarea for telor īn canalul rotitor
Considerānd o curgere fara frecari īn canalul rotorului si luānd o masa elementara din fluidul care curge īntr-un canal cu palete curbate īnpoi, a carei masa este:
dm = Uds-dn-b,
īn care b este latimea canalului.
Linia medie de curgere a fluidului īntre doua palete este asimilata cu un arc de cerc dupa o raza R.
Pentru usurinta s-a fixat un
Ventilatoare, suflante, turbocompresoare
sistem de coordonate, tangent la cercul de raza R(s) si perpendicular pe ea (pe directia de curgere) (n) īn punctul considerat, apoi fortele care actioaneaza asupra elementului de masa pot fi proiectate dupa cele doua directii, adica: fortele perpendiculare pe directia de curgere (n) si fortele īn directia de curgere (s).
5.3.1.1. Fortele perpendiculare pe directia de curgere
Curgerea īn canal facāndu-se dupa cercul cu raza R , ia nastere o forta centrifugala de forma:
dF =dm -
R
(dF1 =dmRZ'2; Z'R = w)
Dar elementul de masa se roteste cu rotorul deci o alta forta centrifugala actioneaza dupa cercul cu raza r de forma:
dF2 =dm-Z2r
care este dirijata radial.
Componenta ei dupa directia perpendiculara curgerii este:
dF2 cos E dm-Z2r-cos E
In cazul miscarii din rotor, elementul de masa dm este supus fortei Coriolis, de semn contrar fortei centrifugale, dupa cercul cu raza R , deci:
dF3 = dm ■ 2Zw
Rezultanta acestor trei forte masice este echilibrata de forta de presiune creata īn
sectiunea respectiva si care este perpendiculara pe directia de curgere.
Aceasta forta de presiune, de echilibrare, este:
wp dPn = - -dn-ds-b = dF1+dF2 cosE- dF3
wn
sau:
![]()
![]()
![]()
Gradientul presiunii statice, perpendicular pe directia de curgere, este: |
dn -ds -b - dm
wn
w
vZ r cos E Z w
( I w
dn-ds-b- U vZ r cos E Z w
R
w p
= p vZ rcosE-2Z w
wn y R y
Ventilatoare, suflante, turbocompresoare
5.3.1.2. Fortele pe directia curgerii
Pe directia curgerii actioneaza ca forta masica, componenta fortei centrifugale masice, dF2:
dK = dm -rZ2 -sinE Variatia presiunii pe directia curgerii, determina o forta de presiune care actioneaza asupra masei de fluid dinspre exterior si care are forma:
dP w p ds-dn-b
ws
Rezultanta acestor doua forte, conform legii lui Newton, actioneaza asupra masei de fluid si deci:
dt
|
wp |
|
dw |
U.b.dn-ds- = U-b-dn-ds-rZ 2 sin E-b-dn-ds-^;
Considerand ca:
si: rezulta:
dt ws dt ws sinE-ds = dr
ww dr wp
U-w-p-rw----- ----- -------
ws ds ws
U-w-dw-U-rw2 -dr-dp
sau:
|
|
U-w-dw-U-rZ2 -dr + dp-0
w-dw-Z 2 r-dr-\------- = 0
U
Prin integrarea acestei ecuatii se obtine ecuatia energiei relative rotitoare:
pw2 u2
-l----- ----- ----- H - const.
|
Aceasta ecuatie se deosebeste de ecuatia energiei curgerii asolute rotitoare a lui Bernoulli, care este de forma: |
U 2 2
Ventilatoare, suflante, turbocompresoare
p+w = ptot = const.
U U
Cāt priveste H , acesta este constant īn īntregul spatiu de curgere si ca urmare prin diferentierea ecuatiei (284) dupa directia normala curgerii, se obtine:
w H-1 w p w w-w u-
De aici rezulta:
wp wn
|
wn |
U
|
w |
wu ww
wn
stiind ca:
u Zr; dn
dr cos E
rezulta:
wp
U wn
rZ2 cos E w
ww wr
5.3.1.3. Ecuatia diferentiala a curgerii relative rotitoare
Prin egalarea relatiilor (283) si (285), rezulta ecuatia diferentiala a curgerii relative rotitoare:
|
|
w w = 2Z-w
wn R
Aceasta relatie este valabila pentru palete curbate īnapoi.
Pentru cazul paletelor curbate īnainte (E >90) īn acelasi mod se obtine expresia:
w w = -2Z--
wn R
In cazul curgerii fara rotatie (Z = 0) w = v si ecuatia (286) devine:
dn R De aici rezulta prin integrare, pentru curgere dupa un cerc, fara rotatie si cu turbinare constanta, cunoscuta lege:
r ■ v = const.
5.3.2. Determinarea aproximativa a curgerii relative īn canal
Rezolvarea ecuatiei (286) nu este posibila, deoarece nu se cunoaste legea de variatie a vitezei relative w , precum nici a razei R .
Ventilatoare, suflante, turbocompresoare
Din aceasta cauza, pentru rezolvarea ecuatiei, se utilizeaza o metoda aproximativa. Consideram ecuatia diferentiala a curgerii pentru paletele curbate īnapoi:
w w _2Z_w = 2Z R-w
R
wn R
Prin separarea variabilelor obtinem:
|
wn R |
|
|
ww ZR-w
Prin integrare expresia devine:
|
|
n
V ' R
Pentru n
= 0 witeza relativa pe directia mediana a canalului rotitor este w = w = wf
. Valoarea constantei de integrare poate fi exprimata astfel:
C = -ln(2ZR-w)
Substituind ultima expresie īn relatia (287) obtinem:
ZR-w n
2 ZR - w R
sau:
2
ZR-w 2ZR-w
e
n
n
Prin dezvoltarea īn serie a termenului e R si neglijānd termenii cu puteri mai mari de 2, se poate aproxima valoarea ultimei egalitati:
De aici rezulta ca:
2ZR-w = (2ZR -w\
n R
sau:
w = 2Z R-(2Z R-wl1
n R
respectiv:
w =
w
n R
Zn
Se observa ca se obtine o variatie liniara a vitezei relative īn functie de latimea canalului rotitor dupa directia transversala de curgere. Pentru:
n = -
w = w' =
w
h 2R
Z h
Ventilatoare, suflante, turbocompresoare
n
w = w'=
w
h
Zh
Variatia vitezei relative , dupa directia normala la cugere este:
|
|
|
|
Aw = w"-w'=2Zh-
Pe masura ce se mareste latimea canalului se reduc si vitezele astfel īncāt la un moment dat viteza pe fata activa poate deveni w' 0 . Aceasta corespunde latimii critice a canalului. Peste aceasta latime apare viteza de īntoarcere. Pentru a evita īntoarcerea fluidului īn canal se utilizeaza o varianta constructiva prevazuta cu doua rānduri de palete - unul lung si unul scurt ( cel din urma asigura o latime de curgere, la iesirea din coroana radiala, inferioara latimii critice).
|
|
Fig. 5.10. Repartizarea vitezei relative si a vitezei medii īntr-un canal rotitor
Fig. 5.11. Canal radial rotitor, cu dou a rāduri de palete
Ventilatoare, suflante, turbocompresoare
5.3.3.1. Factorul de diminuare a sarcinii
Din cele aratate anterior reiese ca latimea canalului nu trebuie sa fie prea mare, pentru ca repartizarea vitezelor, perpendiculare pe directia curgerii, sa poata fi considerata ca variind liniar.
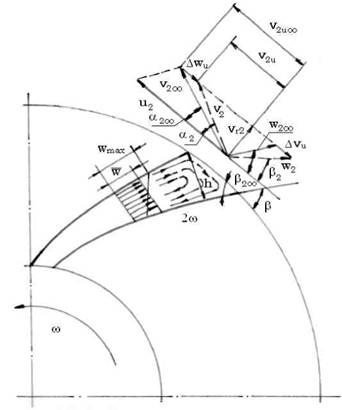 Aceasta reprezentare liniara duce la
introducerea vitezei medii si a unei miscari circulare relative
īn interiorul canalului, a carui viteza unghiulara este 2Z.
Aceasta reprezentare liniara duce la
introducerea vitezei medii si a unei miscari circulare relative
īn interiorul canalului, a carui viteza unghiulara este 2Z.
Miscarea circulara īn canalul rotitor da nastere la o componenta Awu, care se manifesta la iesirea din canal, īn sens invers miscarii de rotatie u2.
Viteza medie liniara a miscarii circulare reiese din relatia:
h
|
w |
w + Z
|
w |
De unde:
|
max |
|
|
w
|
Z |
|
|
Fig. 5.13. Triunghiul vitezelor īn cazul curgerii cu un numar infinit si finit de palete
Dupa Stodola, valoarea medie a componentei Awu este egala cu valoarea medie a vitezei miscarii circulare īn canal:
Awu
Z
Latimea canalului h se deduce din fig.5.13:
2-S-r
|
h |
sin E
z
2f
Din triunghiul vitezelor se deduce:
^u=v2uf-v2u=Awu
Aici Avu este o marime cu care se micsoreaza sarcina ca urmare a numarului finit de palete, cānd apare miscarea de rotatie īn canal (turbioane). Cu aceasta, Avu devine:
Ventilatoare, suflante, turbocompresoare
|
Sr |
|
|
Awu S r2 sin E f Z u2-.sinE
zz Facānd raportul sarcinilor teoretice (fara frecare), īn cazul numarului finit si infinit de palete, se obtine asa numitul coeficient de reducere al sarcinii P
H
|
P |
|
|
|
H |
t
|
|
tf
Fig. 5.14. Factorul de diminuare a sarcinii la debit zero (dup a Stodola)
In cazul intrarii fara turbioane (intrarea radiala ) sarcina este:
Ht u2 v2u si Htf u2v2uf de unde:
|
uv 2u f |
P
u2v2u u2v2u f-^u Avu u2
uv uv
2 2uf 22u f
unde v2u este valoarea medie a componentei tangentiale a vitezei absolute din canal,
īn cazul numarului finit de palete.
Cu ajutorul relatiilor si factorul de diminuare a sarcinii P poate fi
pus sub o forma simpla:
2-S
sin E2 f
|
|
P 1-z
\ f
Pentru O 0 (debit zero) \f 2 deci independent de unghiul E f (fig.5.4.), se obtine:
S
|
|
P 1_S.sinE
z
Aceasta relatie este reprezentata grafic īn fig.5.14.
Ventilatoare, suflante, turbocompresoare
In timp ce Stodola ia īn considerare numai miscarea turbionara relativa. B.Eck, considera si influenta fortelor centrifugale īntr-o sectiune perpendiculara pe directia de miscare relativa si gaseste o relatie mai exacta pentru calculul factorului de reducere a sarcinii P
La fel ca la Stodola, se considera o repartizare liniara a vitezelor relative īn canal si o miscare de rotatie a īntregului curent din canal, care are la iesire viteza unghiulara Z (fig.5.15)
|
|
Fig. 5.15. Calculul factorului de reducere a sarcinii (dupa B. Eck)
|
Z |
|
|
wu a
Aici Z se deosebeste de viteza unghiulara a rotorului Z numai prin aceea ca la diferenta de viteza w cauzata de miscarea de rotatie relativa, luata īn considerare si de Stodola, se mai adauga si influenta curburii paletelor.
Viteza medie a acestei miscari rotitoare, relative, īn canal, trebuie sa fie, ca si la Stodola - egala cu micsorarea componentei tangentiale .
Se obtine astfel:
|
Z a |
|
a= |
|
wu |
|
|
Aw>a=Aw
22 a4 4 Prin acesta calculul devine mai simplu, deorece se considera o repartizare constanta a presiunilor īn lungul conturului paletei. Diferenta de presiune dintre partea inactiva si partea activa a paletei, conform ecuatiei lui Bernoulli este:
|
2 V |
|
2 V |
w 12-w 0
w 12-w 0
Aici diferenta de viteza īntre partea inactiva si activa nu este īntre doua puncte situate pe aceeasi raza r ci īntre punctele C si B situate pe rpedicular pe firul mediu de curgere (fig. 5.12).
Daca se aproximeaza w0' w02 care corespunde realitatii de fapt, se obtine
diferenta de presiune:
Ventilatoare, suflante, turbocompresoare
|
p 2 w12+w02w12 w02 U'w2 f- |
Ăp-U
si cu ajutorul relatiei (309):
Ap = 4U-w2 f-Aw
Momentul motor va fi:
M = z\Apr-b-r-dr
r1
r2
Daca se noteaza S = jb-r-dr, pentru Apr = Ap =
const., se obtine:
r1
M = z-Ap-S Pe de alta parte
momentul motor poate fi dedus din relatia:
M = V p tot , Z
unde:
kptot = U u2v2u
īn care v2u este componenta tangentiala a vitezei absolute la iesirea din rotor īn cazul numarului finit de palete:
Cu aceasta precizare rezulta:
v = v
2u 2u f
Av
M = V'U'u2'v2u U S d b v v2
Z 2 2r 2
Conform relatiilor (310)si (311) se obtine:
unde:
Sd ■ b2 ■ v . v Sd2 -b2-v2u
Av = v2u-v2u - 2r 2u =sinE 2
8z . S . w2f 8z . S
v- = sinE2
w 2f
Astfel pentru coeficientul de diminuare a sarcinii rezulta relatia:
|
vvv v2u z S E2 |
P = 2u = 2
v v + Av Av S db
Daca se considera ca vr r - const., deci b -r = const. se poate scrie:
![]()
![]()
![]()
v r2y |
|
.b |
|
d^\ L r |
S = \(b-rdr = r2-b2r2-r1 = l-d2
Si cu aceasta pentru coeficientul de diminuare a sarcinii rezulta:
Ventilatoare, suflante, turbocompresoare
P
S
2z1-r1r2
sin E
In fig. 5.16 sunt date valorile lui P calculate dupa relatia (313).
|
|
Fig. 5.16. Factorul de diminuare a sarcinii īn cazul rotorului cu b-r = const. ( dupa B. Eck)
Micsorarea sarcinii totale prin numarul finit de palete īnseamna īn primul rānd o reducere a energiei cinetice la iesirea din rotor.
La acelasi rezultat se poate ajunge mai simplu luānd īn considerare gradul de reactie k, relatia (278):
k =1
2u
Facānd rapoertul v - P 2u f < v , se obtine:
u2u2u2
k<k
Din expresia anterioara rezulta ca sarcina statica nu se micsoreaza īn aceeasi masura ca sarcina totala.
Pentru constructia unui rotor cuplat cu difizor este de mare importanta determinarea unghiului de iesire din rotor D
Ventilatoare, suflante, turbocompresoare
Din triunghiul vitezelor (fig. 5.14) rezulta:
tgD 2r
unde:
2u
Se obtine:
tgD
|
O |
1v2r u2
P u2 v2u f P-\f
5.3.3.2. Influenta frecarii asupra sarcinii
Curgerea prin canal s-a aratat ca se face cu viteze diferite, ceea ce atrage dupa sine pierderi prin frecare diferite si anume īn partea activa vitezele fiind mai mici, pierderile prin frecare vor fi mai mici (proportionale cu patratul vitezei), iar īn partea inactiva invers.
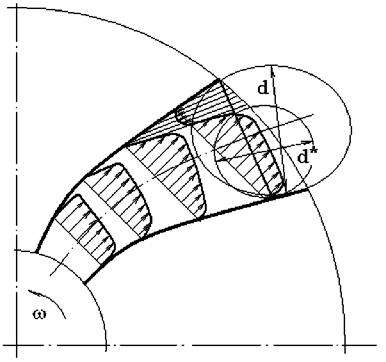
Fig. 5.17. Repartizarea vitezelor real e īn canal si influenta latimii canalului
d - latimea construita; d* - latimea reala
Aceasta stare de lucruri se mentine pāna la o anumita limita a latimii
canalului. Daca aceasta latime h creste, aceste considerente nu mai sunt valabile.
Cum, de regula, canalele se largesc spre exterior, iesirea din canal se face asa cum
arata fig. 5.17.
Din fig. 5.17 se observa ca la iesire numai o portiune din latimea canalului este folosita pentru curgere, iar restul este ocupata de zona turbioanelor.
Ventilatoare, suflante, turbocompresoare
Considerānd ca latimea construita a canalului este h si cea reala (activa) h*, raportul lor este :
h*
y
h
In acest caz factorul de reducere a sarcinii va avea forma:
|
(313.a) |
P =
t S
sin E2f
h 2z1-r1r2
Aici s-a considerat un rotor pentru care: b-r = const.
5.7.4. Camera spirala
Pentru transformare energiei cinetice īn energie potentiala, deci pentru reducerea vitezei curentului de gaz, dupa ultima treapta (sau o treapta intermediara) se ataseaza camera spirala.
|
|
Fig.5.32. Camera spirala
Calculul camerei spirale se face prin doua metode: - pe baza constantei momentului cantitatii de miscare
r ■ vu = const. - pe baza variatiei vitezei medii īn sectiune.
Ventilatoare, suflante, turbocompresoare
Ambele metode utilizeaza ipoteza ca debitul īntr-o sectiune oarecare a camerei spirale, caracterizata prin unghiul M este:
V V. MV.M
M UM 360 UM 2-S
U U
unde:
V debitul volumic total la iesirea din difuzor;
UM si U densitatile agentului de lucru;
MD si M unghiul īn grade, respectiv radiani.
5.7.4.1.Calculul dupa legea r-vu const.
Daca r3 si b3, sunt raza si latimea la intrare īn camera spirala, iar b latimea la raza r (fig.5.32) se poate scrie:
v u r v 3u r 3
|
V M |
|
.b-dr |
v3 |
r dr Mb~ |
|
V UM |
2-S |
v3ur |
r4 |
dr r |
|
U |
|
|
|
|
de unde:
v3 * r3 ' 2 * 71 r d,Y
M^^_------------- UM b
V U J r
In practica se poate considera UM U si atunci:
v3 r3 2 * S dr
MiL----- ----- ---- b_ (378a)
V J r
sau:
|
M v3ur3 r4 b (378b) |
r4
V J r in care:
t v3r
g D3 2.S.r3.v3u-b3 v3u
Relatia (378) este generala, indiferent de forma sectiunii camerei spirale.
Ventilatoare, suflante, turbocompresoare
a) Camera spirala cu pereti paraleli b b3
Din relatia (379) rezulta:
|
tgD3r3 r tgD r3 |
M
|
r dr |
1r4dr r4
ln
|
|
de unde:
1 rdr
M \b
b3tg-D3r r
Fig. Camera spirala cu bb3
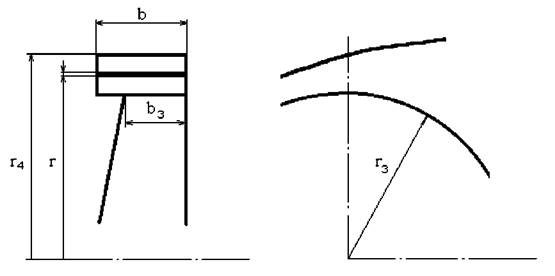
Fig. Camera spirala cu pereti paraleli b b3
Ventilatoare, suflante, turbocompresoare
Camera spirala, cu pereti paraleli, se utilizeaza mai putin īn practica, din cauza dilatarii radiale prea mari.
Pentru a elimina acest dezavantaj se foloseste camera spirala tot cu pereti paraleli, dar cu latime mai mare decāt a difuzorului, b > b3 (fig.5.34.)
In acest caz se obtine:
b r4 dr b r
M ln 4
b3 . tgD3 Jr r b3- tgD3 r3
l r^b.M.tga v.b.M
r3 b v3u b
b) Camera spirala cu sectiune transversala circulara
Daca īn relatia (378) se considera UM= U si unghiul M se ia īn grade, se obtine relatia (378b):
360-v3u-r3r4 dr b
V J r
r3
Notānd cu r' departarea centrului sectiunii circulare de axa rotorului si cu R raza cercului īn sectiune transversala (fig.5.32.) latimea b la departarea r fata de axa, rezulta din expresia:
|
(r-rJ=R |
b = 2^R2-(r-r Cu acesta, pe baza relatiei (378b) rezulta:
720-v3ur3r;}RjR2-(r-r 720S-v -r3 ( ' / '2 n2 \
D= y 1 dr= lr -<Jr R 2 )
|
|
V r Q V
r -R
C(r'-Jr2-R2\ unde:
|
C |
720.S{v3u-r3)
V
Cu aceasta unghiul MD apare ca functie de raza R a cercului sectiunii transversale.
De regula se exprima R ca functie de MD, pentru acesta, prin rezolvarea ecuatiei (383) se obtine :
Ventilatoare, suflante, turbocompresoare
R
C
2r3Mo
C
dar cum:
r'= r3+R, din ecuatia (384) rezulta:
R
C
2r3Mo
C
5.7.4.2. Calculul pe baza variatiei vitezei medii
Pentru cazul cānd se cunoaste aria A si centrul sectiunii transversale ale camerei spirale se recomanda calculul pe baza vitezei medii.
Dupa relatia (376) se calculeaza vu īn centrul sectiunii transversale si se
identifica vu cu vmed , pentru respectiva sectiune. Astel din ecuatia continuitatii rezulta:
|
MD |
|
|
|
|
|
V |
|
V |
|
u med |
A-v
si unghiul cautat M
MD
A-v umed
V
Ventilatoare, suflante, turbocompresoare
6. REGLAREA TURBOMASINILOR
Din studiul curbelor caracteristice ale turbomasinilorlor, a reesit ca se deosebesc doua domenii de functionare a acestora si anume:
domeniul stabil - care se extinde pentru debitul critic; domeniul instabil - pentru debite mai mici decāt debitul critic. Ca urmare si reglarea turbomasinilor trebuie sa cuprinda cele doua domenii de functionare, deoarece parametrii realizati (debitul si presiunea) trebuie sa corespunda cerintelor retelei.
Modurile de realizare a reglarii turbocompresoarelor se dau īn schema urmatoare: Reglarea turbocompresoarelor:
A. domeniul stabil:
A1 prin turatie :a) la presiune de refulare constanta;
b) la debit de aspiratie constant; A2 prin laminare: a) la presiunea de refulare constanta;
b) la debit de aspiratie constant; A3 prin īnclinarea paletelor: a) aparatului director la intrare;
b) rotorului;
c) difuzorului; A4 prin īntoarcere
B. domeniul instabil: -B1. prin refulare īn atmosfera;
-B2. prin refulare īn aspiratie; -B3. prin tot sau nimic.
6.1. Domeniul stabil
In domeniul stabil al curbei caracteristice, reglarea turbomasinilor se face de regula prin turatie, laminare si īnclinarea paletelor.
6.1.1. Reglarea prin turatie
Pentru īntelegerea problemei reglarii turbomasinilor īn fig.6.1. se dau marimile de stare ale unei turbomasini, īntr-o instalatie.
Debitul volumic V0, presiunea p3 si turatia n, pentru un anumit tip de turbomasina sunt legate īntre ele prin curba caracteristica.
Ventilatoare, suflante, turbocompresoare
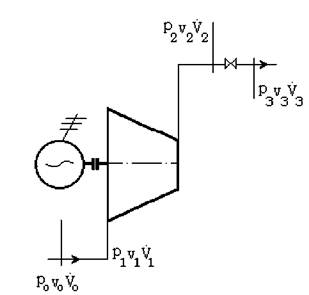
Fig. 6.1. Schema unei turbomasini cu m arimile de stare caracteristice 6.1.1.a. La presiune de refulare constanta
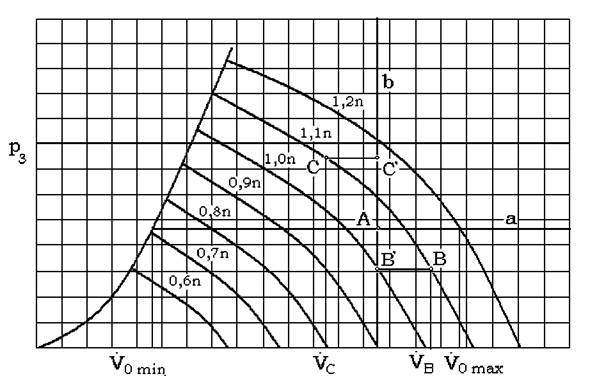
Fig. 6.2.a. Caracteristica unei tur bomasini radiale cu reglarea prin varia tia turatiei la
p3 const.
De multe ori se pune problema ca presiunea de refulare a turbomasinilor sa fie constanta.
Ventilatoare, suflante, turbocompresoare
Asa dupa cum rezulta din fig. 6.2.a. linia a de presiune constanta, poate fi realizata prin variatia turatiei īntre 0.9n si 1.2n , cānd debitul variaza īntre V0 min si
V max .
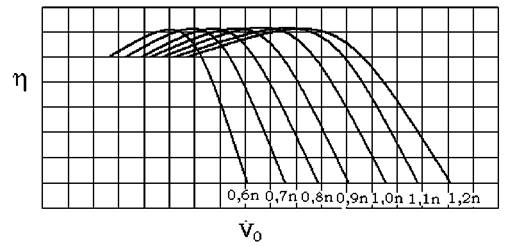
Fig. 6.2.b. Variatia randamentului turbomasin ilor radiale functie de debitul aspirat 6.1.1.b. La debit de aspiratie constant
In mod analog ca īn cazul anterior mentinerea constanta a debitului (linia b ,fig. 6.2.a.), poate fi realizata prin variatia turatiei īntre 0.9n si 1.2n .
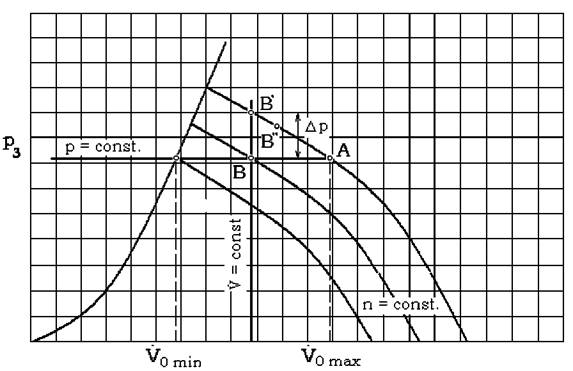
Fig. 6.3.a. Caracteristica unei turbomasini radiale cu reglare prin laminare
Ventilatoare, suflante, turbocompresoare
6.1.2. Prin laminare
Daca turatia turbomasinii nu se poate modifica, atunci ramāne posibilitatea de reglare prin laminare.
6.1.2.a. La presiune de refulare constanta
Prin laminare īn conducta de aspiratie sau de refulare este posibil sa se mentina presiune p3 constanta prin variatia debitului, cānd punctul de functionare se va gasi sub curba caracteristica la n const. Cel mai mare debit volumic la presiunea p3 va fi V0 max (fig. 6.3.a.), cānd organul de laminare este complet deschis.
Daca laminarea se petrece īn conducta de refulare (fig.6.3 c) atunci volumul aspirat se micsoreaza din punctual A cānd este V0 max , pāna la punctual de
functionare B' cānd este V0 . In sistemul de laminare se produce o cadere de presiune, de la B' la B si īn final turbomasina functioneaza cu presiunea p3.
In acelasi fel se poate concepe reglarea prin laminarea, īn conducta de aspiratie, printr-o clapeta, cānd punctual A se muta īn punctual B (fig 6.3 b).
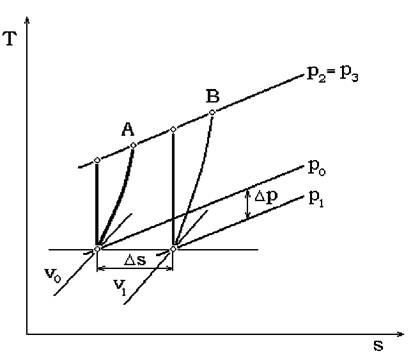
Fig. 6.3.b. Reglarea prin laminare īn conducta de aspira tie
Reglarea prin laminare fata de reglarea prin turatie este mai dezavantajoasa īntrucāt duce la un consum mai mare de energie. Punctul B este la dreapta punctului
Ventilatoare, suflante, turbocompresoare
B' , īntrucāt prin laminare, īn conducta de aspiratie se produce o micsorare a densitatii si, ca urmare, la acelasi debit masic, debitul volumic va fi mai mare.
In fig.6.3.b. si fig.6.3.c. se arata reglarea prin laminare, īn cele doua cazuri, cu reprezentarea proceselor īn diagrama T - s .
6.1.2.b. La debit de aspiratie constant
Asa cum rezulta din fig.6.3.a. si fig.6.3.c, prin variatia presiunii p3, datorita laminarii īn conducta de aspiratie sau refulare, se poate mentine constant debitul volumic V0.
Fig. 6.3.c. Reglarea prin laminare īn conducta de refulare 6.1.3. Prin īnclinarea paletelor
Prin variatia īnclinarii paletelor aparatul director la intrare, ale rotorului si difuzorului, separat sau īmpreuna, se poate modifica īn limite largi debitul si raportul de comprimare.
Reglarea prin variatia īnclinarii paletelor aparatului director, la intrarea sau a difuzorului, se poate aplica atāt la turbomasinile radiale cāt si axiale, dar reglarea prin īnclinarea paletelor rotorului se poate face numai la turbomasinile axiale.
Ventilatoare, suflante, turbocompresoare
6.1.4. Prin īntoarcere
In multe cazuri este necesar ca debitul refulat de o turbomasina sa fie reglat īntre anumite limite. Aceasta reglare se poate face prin reīntoarcerea unei parti din debitul de agent, dupa prima sau a doua treapta a turbomasinii, la aspiratie, astfel īncāt īn
treptele urmatoare va circula un debit mai
|
|
mic, asa cum se reprezinta schematic īn
fig.6.4.
Ventilul de īntoarcere poate fi
actionat prin traductorul de debit sau de
presiune.
In cazul reglarii prin īntoarcere, pierderile
sunt mai mici decāt īn cazul reglarii prin
laminare.
Fig. 6.4. Schema de reglare prin īntoarcere
6.2. Domeniul instabil
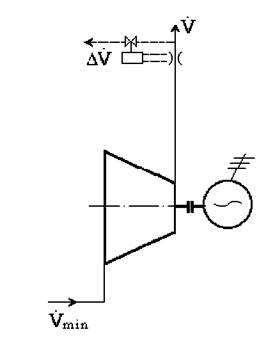
Fig. 6.5. Schema reglarii prin refulare īn atmosfera
La functionarea unei turbomasini pe ramura instabila a caracteristicii sale, apare fenomenul de pompaj, caracterizat prin oscilatii din cauza īntoarcerii curentului de agent de lucru.
De aceea īn practica fenomenul de pompaj trebuie eliminat prin diferite dispozitive.
6.2.1. Prin refulare īn atmosfera
La reglarea prin refularea īn atmosfera, aratata schematic īn fig. 6.5., pompajul este īndepartat printr-un ventil plasat pe conducta de refulare. Prin acest ventil, īn cazul cānd se atinge limita de
Ventilatoare, suflante, turbocompresoare
pompaj, o parte din debit este eliminat īn atmosfera si deci pericolul de pompaj este īnlaturat. Debitul refulat īn atmosfera este diferenta dintre debitul minim de aspiratie
Vmin si debitul livrat īn sistemul de conducte V (AV = Vm
V
Consumul de putere al compresorului īntre V = 0 si V = Vmin este constant.Acest
sistem de reglare se foloseste īmpreuna cu reglarea la presiune constanta sau cu reglarea la debit constant.
6.2.2. Prin refulare īn aspiratie
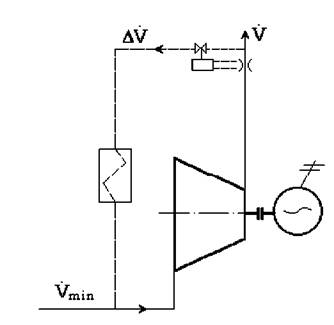
Fig. 6.6. Schema reglarii prin refulare īn aspira tie
La reglarea prin refulare īn aspiratie, o parte din debitul volumic refulat, este dirijat printr-un ajutaj īn conducta de aspiratie. In ajutaj energia potentiala se transforma īn energie cinetica si ca urmare o parte din energia consumata pentru comprimare este recuperata. De asemenea, pentru a nu influenta temperatura de aspiratie, se introduce si un racitor īn circuitul de īntoarcere.
Reglarea prin refularea īn aspiratie se foloseste īn cazul agentilor de lucru toxici sau scumpi.
6.2.3. Prin tot sau nimic
Acest sistem de reglare se bazeaza pe deconectarea de la retea cānd consumul de agent refulat se reduce.
Daca debitul volumic se reduce pāna aproape de limita de pompaj, atunci traductorul de debit a , comanda servomotorul c , care deschide ventilul b .
Prin aceasta presiune finala p2 va fi mai mica decāt presiunea retelei p3 si
ventilul de retinere d va fi īnchis. In acelasi timp servomotorul e actioneaza asupra clapetei f din conducta de aspiratie si o deschide numai atāt īncāt sa compeseze
pierderile prin ventilul b . In acest timp presiune p3 scade la o presiune p3 min care actioneaza asupra traductorului de presiune, si care la rāndul lui comanda īnchiderea
Ventilatoare, suflante, turbocompresoare
ventilului b .Clapeta de laminare f ramāne īnsa deschisa. Presiunea de refulare p2 a turbomasinii īncepe sa creasca, devine mai mare decāt presiunea p3 a retelei si se
deschide ventilul de retinere d.
De aici īnainte turbomasina īncepe sa functioneze normal.
Fig. 6.7. Schema reglarii prin"tot sau nimic"
a - traductor de debit;
b - ventil de evacuare;
c - servomotor;
d - ventil de retinere;
e - servomotor;
f - clapeta de laminare;
g - traductor de presiune
|