1. Statistinis ir termodinaminis tyrimo metodai
Kuo termodinaminis ir statistinis ( molekulinis - kinetinis) makrosistemų tyrimo metodai kokybiskai skiriasi ir papildo vienas kitą?
Pagrindinis molekulinės fizikos, kaip mokslo, tyrimo objektas yra statistinis. Todėl tik daugelio dalelių sistemai būdingos tokios savybės, kurios apibūdinamos fizikiniais dydziais: temperatūra, slėgiu, siluminiu laidumu, klampa ir pan. Jie isreiskia vidutinį atskirų molekulių poveikį. Termodinamika - fizikos mokslo saka, tirianti makroskopinių kūnų sistemas siluminiu poziūriu, nesigilinant į jose vykstančių reiskinių mikroskopinę prigimtį. Todėl termodinaminis tyrimo metodas taikomas sistemos vienos rūsies energijos virsmams kitos rūsies energija nagrinėti. Pačią termodinaminę sistemą sudaro vi 545x236f suma makroskopinių kūnų, kurie sąveikauja tarpusavyje ir su kitais kūnais ir dėl to keičiasi energijos. Pagrindinis termodinaminio metodo tikslas - istirti termodinaminės sistemos būseną.
4.Kaip aiskinami dujų slėgis, termodinaminė temperatūra molekulinės - kinetinės teorijos poziūriu?
Idealiųjų dujų slėgis lygus 2/3
vidutinės slenkamojo judėjimo kinetinės energijos, kurią
turi tūrio vienete esančios molekulės ![]() čia S - sienelės plotas, ΔK/Δt - sienelės impulso kitimo sparta.
čia S - sienelės plotas, ΔK/Δt - sienelės impulso kitimo sparta. ![]() .Molekulės slenkamojo judėjimo vidutinė
kinetinė energija proporcinga idealiųjų dujų
temperatūrai ir yra jos matas. Pasiekus absoliutaus nulio
temperatūrą (T = 0 K), dingsta molekulių chaotiskas
judėjimas, taigi dingsta ir slėgis idealiose dujose, nes, kaip seka
is israiskų, slėgis proporcingas temperaturai:
.Molekulės slenkamojo judėjimo vidutinė
kinetinė energija proporcinga idealiųjų dujų
temperatūrai ir yra jos matas. Pasiekus absoliutaus nulio
temperatūrą (T = 0 K), dingsta molekulių chaotiskas
judėjimas, taigi dingsta ir slėgis idealiose dujose, nes, kaip seka
is israiskų, slėgis proporcingas temperaturai: ![]() .Tačiau jokiais cheminiais ir fizikiniais būdais T
= 0 K temperatūra nepasiekiama.
.Tačiau jokiais cheminiais ir fizikiniais būdais T
= 0 K temperatūra nepasiekiama.
7.Kaip, zinant dujų molekulių pasiskirstymo funkciją pagal greičius, galime rasti pasiskirstymo funkciją pagal energijas?
Is molekules
kinetines energijos formules ![]() isreiske greiti
isreiske greiti ![]() jo pokyti
jo pokyti ![]() ir siuos dydzius irase i
ir siuos dydzius irase i ![]() formule gauname
molekulių statistinio pasiskirstymo pagal slenkamojo judėjimo
kinetines energijos vertes funkcija
formule gauname
molekulių statistinio pasiskirstymo pagal slenkamojo judėjimo
kinetines energijos vertes funkcija ![]()
9.Kaip keičiasi atmosferos slėgis didėjant auksčiui?
![]() čia ρ - dujų tankis, priklausantis nuo auksčio.
čia ρ - dujų tankis, priklausantis nuo auksčio.
![]() čia p0
- slėgis jūros lygyje (h = 0). Taigi ji isreiskia
dujų slėgio priklausomybę nuo auksčio, kai kitos
sąlygos nekinta: dujų slėgis kylant eksponentiskai
mazėja. Realiai atmosferos temperatūra kylant mazėja,
mazėja ir kūnų laisvojo kritimo pagreitis g, todėl formulė
yra tik orientacinė ir tinka nestoriems atmosferos sluoksniams.
čia p0
- slėgis jūros lygyje (h = 0). Taigi ji isreiskia
dujų slėgio priklausomybę nuo auksčio, kai kitos
sąlygos nekinta: dujų slėgis kylant eksponentiskai
mazėja. Realiai atmosferos temperatūra kylant mazėja,
mazėja ir kūnų laisvojo kritimo pagreitis g, todėl formulė
yra tik orientacinė ir tinka nestoriems atmosferos sluoksniams.
10.Uzrasykite ir paaiskinkite Bolcmano pasiskirstymo dėsnį. Kuo skiriasi Maksvelio ir Bolcmano pasiskirstymo dėsniai?
Dujų
slėgis proporcingas molekulių koncentracijai.Bolcmano skirstinys 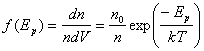 čia n -
molekulių skaičius sistemoje. Be to Bolcmanas įrodė, kad
sis skirstinys teisingas bet kuriame stacionariame isorinių
potencialinių jėgų lauke, o ne tik gravitaciniame. didėjant
dalelių energijai, jų skaičius eksponentiskai mazėja.
Bolcmano skirstiniu paaiskinamas kvantinių stiprintuvų ir generatorių veikimas. Maksvelo skirstinys
reiskia molekuliu pasiskirstyma pagal ju siluminio greicio vertes pusiausvyroje
termodinamineje sistemoje.Skirstinio esme;daugelio molekuliu greicio vertes
artimos tam tikrai tikimiausiojo greicio vertei
čia n -
molekulių skaičius sistemoje. Be to Bolcmanas įrodė, kad
sis skirstinys teisingas bet kuriame stacionariame isorinių
potencialinių jėgų lauke, o ne tik gravitaciniame. didėjant
dalelių energijai, jų skaičius eksponentiskai mazėja.
Bolcmano skirstiniu paaiskinamas kvantinių stiprintuvų ir generatorių veikimas. Maksvelo skirstinys
reiskia molekuliu pasiskirstyma pagal ju siluminio greicio vertes pusiausvyroje
termodinamineje sistemoje.Skirstinio esme;daugelio molekuliu greicio vertes
artimos tam tikrai tikimiausiojo greicio vertei ![]() .
.
11.Kaip priklauso dujų molekulių vidutinis laisvasis lėkis nuo slėgio?
![]() . Vidutinis laisvasis lėkis
tuo mazesnis, kuo didesnis molekulės efektinis skersmuo (molekulių
greičiai mazi, zema temperatūra), ir atvirksčiai proporcingas
dujų slėgiui (kai temperatūra nekinta). Normaliomis
sąlygomis (K273=T, ) daugumos dujų p= Pa , l yra 10-7
m eilės dydis, o molekulių susidūrimų daznis ν
siekia 1010 s-1.
. Vidutinis laisvasis lėkis
tuo mazesnis, kuo didesnis molekulės efektinis skersmuo (molekulių
greičiai mazi, zema temperatūra), ir atvirksčiai proporcingas
dujų slėgiui (kai temperatūra nekinta). Normaliomis
sąlygomis (K273=T, ) daugumos dujų p= Pa , l yra 10-7
m eilės dydis, o molekulių susidūrimų daznis ν
siekia 1010 s-1.
12.Suformuluokite tolygaus energijos pasiskirstymo pagal laisvės laipsnius dėsnį. Kodėl svyravimų laisvės laipsniui tenka dvigubai daugiau energijos, lyginant su laisvės laipsniais slenkamajam ir sukamajam judėjimui?
Termodinamines pusiausvyros busenoje slenkamojo, sukamojo ir virpamojo judėjimo vienam laisves laipsniui tenka vidutiniskai vienodas kinetines energijos kiekis, lygus ½*kT.Tai kinetines energijos tolygaus pasiskirstymo pagal laisves laipsnius statistinis desnis.Siame desnyje kalbama apie vienam laisves laipsniui tenkančia vidutine kinetines energijos verte.vienos daleles kinetines energijos vidurkis laiko atzvilgiu sutampa su atskiru daleliu energijos verciu tuo paciu laiko momentu vidurkiu.Kartais minetasis desnis teisingas potencinei energijai.kai molekuliniu sistemoje atomai virpa tarp saves nesuderintai, tuomet statistikai puse visos sistemos virpesiu energijos yra kinetine ir puse kinetine..Siuo atveju kiekvienam virpamojo judėjimo laisves laipsniui vidutiniskai tenka ½*kT kinetine energija ir lygiai tokia pat potencine energija .Taigi vienam virpamojo judėjimo laisves laipsniui vidutiniskai tenkantis energijos kiekis lygus kT.
13.Kas lemia idealiųjų dujų vidinę energiją? Kokių procesų metu gali keistis dujų vidinė energija?
Duju vidine
energija priklauso nuo molekules laisves laipsniu skaicius bei absoliutines temperatūros ir pastarajai
nekintant yra pastovi.Bet kokios mases m ideliuju duju vidine energija uzrasoma
taip:![]() cia
cia ![]() - yra moliu skaicius.Kaip matome ideliuju duju vidine
energija nepriklauso nuo ju uzimamo turio.
- yra moliu skaicius.Kaip matome ideliuju duju vidine
energija nepriklauso nuo ju uzimamo turio.
14.Ką vadiname dujų silumine talpa? Kuo skiriasi CP ir CV? Kurio vertė yra didesnė?
Medziagos
siluminė talpa lygi silumos kiekiui, kurį suteikus kūno
temperatūra padidėja 1 K: ![]() . Vieno molio medziagos siluminė talpa vadinama jos
moline siluma:
. Vieno molio medziagos siluminė talpa vadinama jos
moline siluma: ![]() . Izochorinis procesas (V=const, dujos nesiplečia):
. Izochorinis procesas (V=const, dujos nesiplečia): ![]() . Izobarinis procesas (const=p):
. Izobarinis procesas (const=p): ![]() . Is idealiųjų dujų būsenos lygties pV/T=m/M*R gauname:
. Is idealiųjų dujų būsenos lygties pV/T=m/M*R gauname: ![]() .Taigi
.Taigi ![]() . Ji rodo, kad izobarinė molinė siluma Cp visada
didesnė uz izochorinę molinę silumą CV dydziu,
lygiu universaliosios dujų konstantos R vertei. Taip yra
todėl, kad sildant dujas izochoriskai suteikiamas silumos kiekis virsta
jų vidine energija, o sildant izobariskai dalis silumos kiekio suvartojama
jų plėtimosi darbui.
. Ji rodo, kad izobarinė molinė siluma Cp visada
didesnė uz izochorinę molinę silumą CV dydziu,
lygiu universaliosios dujų konstantos R vertei. Taip yra
todėl, kad sildant dujas izochoriskai suteikiamas silumos kiekis virsta
jų vidine energija, o sildant izobariskai dalis silumos kiekio suvartojama
jų plėtimosi darbui.
15. Kam yra lygus dujų vieno molio izobarinio plėtimosi atliktas darbas, dujas susildant 1K laipsniu?
Vykstant
izobariniam procesui, nekinta duju slegis todel vieno molio ideliuju duju izobarinio pletimosi darbas lygus ju slegio
ir turio pokycio sandaugai.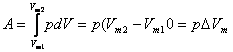
16.Uzrasykite pirmąjį termodinamikos dėsnį diferencialinėje formoje. Jį pritaikykite izochoriniam ir izoterminiam procesams.
Izochorinis procesas
(V=const) p ir V koordinačių sistemoje vaizduojamas
vertikalia tiese (9.19 pav.), nes slėgis siuo atveju proporcingas
temperatūrai: ![]() . Taip sildomos dujos nesiplečia ir darbo neatlieka.
Taigi visas suteikiamas silumos kiekis suvartojamas sistemos vidinei energijai
didinti:
. Taip sildomos dujos nesiplečia ir darbo neatlieka.
Taigi visas suteikiamas silumos kiekis suvartojamas sistemos vidinei energijai
didinti: ![]() . Izoterminis procesas (T=const) p ir V koordinačių
sistemoje vaizduojamas hiperbole, nes, kaip seka is idealiųjų
dujų būsenos lygties
. Izoterminis procesas (T=const) p ir V koordinačių
sistemoje vaizduojamas hiperbole, nes, kaip seka is idealiųjų
dujų būsenos lygties ![]() , jų slėgis atvirksčiai proporcingas
tūriui:
, jų slėgis atvirksčiai proporcingas
tūriui: ![]() . Kadangi sistemos temperatūra nekinta, tai nekinta ir
jos vidinė energija:
. Kadangi sistemos temperatūra nekinta, tai nekinta ir
jos vidinė energija: ![]() . Vadinasi, I t. d. izoterminiam procesui teigia, kad visas
idealiosioms dujoms suteikiamas silumos kiekis suvartojamos jų
plėtimosi darbui:
. Vadinasi, I t. d. izoterminiam procesui teigia, kad visas
idealiosioms dujoms suteikiamas silumos kiekis suvartojamos jų
plėtimosi darbui: 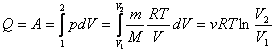
17.Paaiskinkite, įsyla ar atsąla idealiosios dujos, jeigu jos issiplečia, esant pastoviam slėgiui?
Izobarinis procesas
(p=const) p ir V koordinačių sistemoje
vaizduojamas horizontalia tiese nes dujų tūris siuo atveju
proporcingas temperatūrai: ![]() . Dujų izobarinio plėtimosi darbas
. Dujų izobarinio plėtimosi darbas 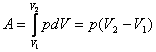 . Jis lygus brūksniuoto
stačiakampio plotui. Dujos plečiasi, nes jos įkaista. Todėl
is būsenos lygties
. Jis lygus brūksniuoto
stačiakampio plotui. Dujos plečiasi, nes jos įkaista. Todėl
is būsenos lygties ![]() .
.
18.Kaip keičiasi dujų temperatūra, joms adiabatiskai plečiantis?
Adiabatinis procesas
(dQ=0), kaip jau minėta, vyksta be silumos mainų su aplinka. I t. d.
adiabatiniam procesui teigia, kad adiabatiskai besiplėsdamos dujos atlieka
darbą, lygų jų vidinės energijos sumazėjimui: ![]() . Vadinasi, adiabatiskai besiplėsdamos dujos
atvėsta (T2<T1). Plėtimosi darbas lygus plotui po adiabate.
Adiabatės lygtis p ir V koordinatėmis (viena is
trijų Puasono lygčių) yra:
. Vadinasi, adiabatiskai besiplėsdamos dujos
atvėsta (T2<T1). Plėtimosi darbas lygus plotui po adiabate.
Adiabatės lygtis p ir V koordinatėmis (viena is
trijų Puasono lygčių) yra: ![]() , cia
, cia ![]() >1 - Puasono koeficientas.
>1 - Puasono koeficientas.
19.Kuo skiriasi grįztamieji ir negrįztamieji procesai? Kodėl realūs procesai yra negrįztamieji?
Termodinaminis ciklas vadinamas grįztamuoju, jeigu įvykus tiesioginiam, o po to tokiam pat atvirstiniam ciklui, į pradinę būseną grįzta ir sistema, ir isoriniai kūnai, su kuriais sistema sąveikavo. Bet kuris pusiausvyrasis procesas yra grįztamasis. Visi realūs procesai pasizymi didesniais ar mazesniais energijos nuostoliais (dėl trinties, siluminio laidumo ar pan.). Todėl jie yra negrįztamieji. Silumos apykaitos procesai, esant baigtiniam temperatūrų skirtumui, taip pat yra negrįztamieji.
20.Grafiskai pavaizduokite Karno ciklą. Kam lygus jo naudingumo koeficientas? Pavaizduokite Karno ciklą diagrama T(S), čia T - temperatūra, S - entropija.
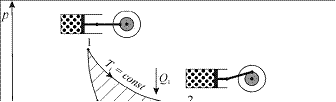
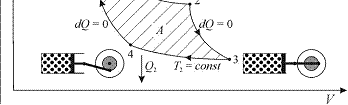
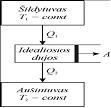
Pirmoji teorema teigia, kad idealiosios grįztamojo Karno ciklo
siluminės masinos naudingumo koeficientas priklauso tik nuo kaitintuvo ir
ausintuvo temperatūrų ir nepriklauso nuo jos konstrukcijos bei darbo
medziagos prigimties. Ciklo naudingumo koeficientas : ![]() . Isvada: idealiuoju Karno ciklu veikiančio siluminio
variklio naudingumo koeficientas priklauso tik nuo sildytuvo ir ausintuvo
temperatūrų T1 ir T2.
. Isvada: idealiuoju Karno ciklu veikiančio siluminio
variklio naudingumo koeficientas priklauso tik nuo sildytuvo ir ausintuvo
temperatūrų T1 ir T2.
22.Ką tvirtina antrasis termodinamikos dėsnis?
Vokiečių
fizikas R. Klauzijus 1850 m. teigė, kad negalimas toks procesas, kurio
vienintelis rezultatas - energijos perdavimas silumos pavidalu is saltesniojo
kūno siltesniajam. Anglų
fizikas V. Tompsonas (Kelvinas) 1851 m. teigė, kad negalimas toks
ciklinis procesas, kurio vienintelis rezultatas - is sildytuvo paimtos silumos
pavertimas jai ekvivalentisku darbu. Vadinasi, ciklinio siluminio variklio
naudingumo koeficientas mazesnis uz vienetą ir negalima sukurti
ciklinį siluminį variklį be ausintuvo. Remdamasis siomis isvadomis
vokiečių fizikas V. Ostvaldas 1888 m. taip suformulavo II t. d.: negalimas
antrosios rūsies amzinasis siluminis variklis. Izoliuotos sistemos
entropija nemazėja: ![]() t.y. izoliuotose
makroskopinėse sistemose termodinaminiai procesai vyksta tik ta kryptimi,
kuria sistemos entropija nemazėja.
t.y. izoliuotose
makroskopinėse sistemose termodinaminiai procesai vyksta tik ta kryptimi,
kuria sistemos entropija nemazėja.
24.Paaiskinkite entropijos sampratą (uzrasykite jos matematinę israiską).
Būsenos
funkcija, kurios diferencialas yra dQ/T,
vadinamas sistemos entropija S. Jos elementarusis pokytis ![]() t. y. lygus elementariajam
redukuotajam silumos kiekiui. Is entropijos elementariojo pokyčio zenklo
galima spręsti apie silumos mainų kryptį sistemoje. Entropijos
pokytis, sistemai grįztamai perėjus is 1 būsenos į 2,
lygus:
t. y. lygus elementariajam
redukuotajam silumos kiekiui. Is entropijos elementariojo pokyčio zenklo
galima spręsti apie silumos mainų kryptį sistemoje. Entropijos
pokytis, sistemai grįztamai perėjus is 1 būsenos į 2,
lygus: ![]() .
.
2. Pernesimo reiskiniai
1.Kokiomis sąlygomis vyksta pernesimo reiskiniai?
Kai
sie procesai vyksta izoliuotoje sistemoje, tai ji dėl kiekvieno jų
savaime artėja į pusiausvirąją būseną, t.y.
į maksimalios entropijos būseną. Taigi pernesimo proceso
esmė - sistemos pastangos pasiekti pusiausvirąją
būseną. Kiekybiskai jis apibūdinamas pernesamojo dydzio kinetinio
srauto tankiu ir relaksacijos trukme. Kinetinio srauto tankis
lygus tankiui fizikinio dydzio I, per 1 s pernestam per statmeną vienetinį plotelį: ![]() . Pernesimas vyksta priesinga gradientui kryptimi.
. Pernesimas vyksta priesinga gradientui kryptimi.
2.Kokį procesą vadiname difuzija? Kokių reikia sąlygų, kad vyktų difuzija? Uzrasykite difuzijos lygtį.
Difuzijos lygtis:![]() . Tai masės pernesimas
dėl molekulių siluminio judėjimo toje pačioje medziagoje (savoji
difuzija) arba susiliečiančiose medziagose (abipusė
difuzija). Difuzija atsiranda dėl molekulių koncentracijos,
temperatūros, slėgio ar elektrinio lauko stiprio gradientų.
Nagrinėjant savąją difuziją, atsirandančią
dėl dujų tankio gradiento, nustatyta, kad pernestos medziagos
masės srauto tankį apibūdina A. Fiko dėsnis: pernestos
masės srauto tankis proporcingas dujų molekulių koncentracijos
gradientui, t.y.
. Tai masės pernesimas
dėl molekulių siluminio judėjimo toje pačioje medziagoje (savoji
difuzija) arba susiliečiančiose medziagose (abipusė
difuzija). Difuzija atsiranda dėl molekulių koncentracijos,
temperatūros, slėgio ar elektrinio lauko stiprio gradientų.
Nagrinėjant savąją difuziją, atsirandančią
dėl dujų tankio gradiento, nustatyta, kad pernestos medziagos
masės srauto tankį apibūdina A. Fiko dėsnis: pernestos
masės srauto tankis proporcingas dujų molekulių koncentracijos
gradientui, t.y. ![]() , čia D - savosios difuzijos koeficientas, kurio
matavimo vienetas m2/ s. Jis lygus masės srauto tankiui, kai
koncentracijos gradientas dn/dx=1.
, čia D - savosios difuzijos koeficientas, kurio
matavimo vienetas m2/ s. Jis lygus masės srauto tankiui, kai
koncentracijos gradientas dn/dx=1.
3.Koks reiskinys vadinamas dujų klampa? Kaip jis aiskinamas?
Klampumą
arba vidinę trintį dujose sąlygoja molekulių impulso
pernesimas tarp gretimų skirtingais greičiais judančių
sluoksnių (10.2 pav.). Dėl to greitesnis sluoksnis lėtėja,
o lėtesnis greitėja. Vadinasi, vienas sluoksnis yra stabdomas, o
gretimas sluoksnis greitinamas. Taip atsiradusios vidinės trinties
jėgos modulis proporcingas sluoksnių greičių gradientui (I
Niutono dėsnis): ![]() čia S -
besiliečiančių pavirsių plotas, η - dinaminės
klampos koeficientas.
čia S -
besiliečiančių pavirsių plotas, η - dinaminės
klampos koeficientas. ![]()
4.Kokį reiskinį vadiname silumos laidumu? Kaip jis matematiskai aprasomas? Kokių reikia sąlygų, kad jis vyktų?
Jeigu per laiko
tarpa dt pro pavirsiaus plota dS pernesama energija dQ tai energijos srautas ![]() .Toki pernesimo
reisini vadiname silumos laidumu.Per laiko vieneta pro temperatūros
gradiento krypčiai statmeno isivaizduojamo pavirsiaus plota dS pernesama
siluminio judėjimo energija yra tiesiogiai proporcinga
temperatūros gradiento ir ploto
sandaugai.Sis empirinis Furje desnis matematiskai uzrasomas taip:
.Toki pernesimo
reisini vadiname silumos laidumu.Per laiko vieneta pro temperatūros
gradiento krypčiai statmeno isivaizduojamo pavirsiaus plota dS pernesama
siluminio judėjimo energija yra tiesiogiai proporcinga
temperatūros gradiento ir ploto
sandaugai.Sis empirinis Furje desnis matematiskai uzrasomas taip:![]()
3. Realiosios dujos ir medziagos kondensuotos būsenos samprata
1.Kuo skiriasi realiosios dujos nuo idealiųjų dujų?
Realiųjų
dujų vidinė energija lygi jų molekulių netvarkingo
judėjimo kinetinės energijos ir tarpusavio sąveikos
potencinės energijos sumai: ![]() . adiabatiskai besiplečiančių
idealiųjų dujų temperatūros pokytis
. adiabatiskai besiplečiančių
idealiųjų dujų temperatūros pokytis ![]() ,adiabatiskai besiplečiančių ir tokį pat
darbą atliekančių realiųjų dujų
,adiabatiskai besiplečiančių ir tokį pat
darbą atliekančių realiųjų dujų 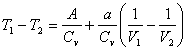 .Vadinasi, adiabatiskai besiplečiančios realiosios
dujos atvėsta daugiau negu idealiosios. Tai reiskia, kad, jeigu taip
plečiasi idealiosios dujos, tai jų ir temperatūra nekinta (
.Vadinasi, adiabatiskai besiplečiančios realiosios
dujos atvėsta daugiau negu idealiosios. Tai reiskia, kad, jeigu taip
plečiasi idealiosios dujos, tai jų ir temperatūra nekinta (![]() ). Realiųjų dujų atveju tai reiskia, kad
). Realiųjų dujų atveju tai reiskia, kad ![]() is cia
is cia ![]() . Kadangi
. Kadangi ![]() , tai ir
, tai ir ![]() . Vadinasi, į tustumą besiplėsdamos
realiosios dujos turi atvėsti.
. Vadinasi, į tustumą besiplėsdamos
realiosios dujos turi atvėsti.
2.Isnagrinėkite sąveikos jėgas veikiančias tarp molekulių.
Molekulių sąveikos traukos jėgos
vadinamos van der Valso jėgomis. Jos yra elektromagnetinės prigimties
ir skirstomos į tris tipus. 1)Orientacinės jėgos būdingos
polinėms molekulėms, kurių teigiamų ir neigiamų
krūvių centrai nesutampa. Tokios molekulės yra elektriniai
dipoliai - arti vienas kito esančių vienodo didumo, bet priesingo
zenklo krūvių sistemos ![]() čia -
čia - ![]() dipolio elektrinio
momento modulis, r - atstumas tarp molekulių centrų, T -
būsenos temperatūra.2) Indukcinės jėgos atsiranda,
kai nepolinę molekulę veikia elektrinio dipolio sukurtas elektrinis
laukas. Dėl to molekulių "+" ir "- " krūvių "centrai"
pasislenka, molekulė tampa dipoliu ir atsiranda dipolinis momentas.
dipolio elektrinio
momento modulis, r - atstumas tarp molekulių centrų, T -
būsenos temperatūra.2) Indukcinės jėgos atsiranda,
kai nepolinę molekulę veikia elektrinio dipolio sukurtas elektrinis
laukas. Dėl to molekulių "+" ir "- " krūvių "centrai"
pasislenka, molekulė tampa dipoliu ir atsiranda dipolinis momentas. ![]() čia α -
molekulės poliarizuojamumas. 3) Dispersinės traukos jėgos būdingos
visoms molekulėms, kaip "momentiniams" elektriniams dipoliams,
atsirandantiems dėl elektronų svyravimų molekulėse.
čia α -
molekulės poliarizuojamumas. 3) Dispersinės traukos jėgos būdingos
visoms molekulėms, kaip "momentiniams" elektriniams dipoliams,
atsirandantiems dėl elektronų svyravimų molekulėse. ![]() Kai molekulių
centrai suartėja iki
Kai molekulių
centrai suartėja iki ![]() , atsiranda ypatinga kvantinė
sąveika, kurios pasekmė - stiprios jėgos, kurias lemia
branduolių elektrostatinė stūma.
, atsiranda ypatinga kvantinė
sąveika, kurios pasekmė - stiprios jėgos, kurias lemia
branduolių elektrostatinė stūma. ![]() .
.
3.Isnagrinėkite Van der Valso lygtį. Kokioms dujoms ji taikoma? Nubraizykite jos teorines ir praktines izotermes.
Van der Valso lygtis sieja realiųjų
dujų, kaip termodinaminės sistemos, būsenos pagrindinius
parametrus. Olandų fizikas J. van der Valsas gavo realiųjų
dujų būsenos lygtį, tikslesnę uz idealiųjų
dujų būsenos lygtį, teigdamas, kad realiųjų dujų
molekules galima laikyti absoliučiai kietais d skersmens rutuliukais,
tarp kurių veikia tik traukos jėgos. Stūmos jėgos
įskaitomos molekulės savuoju efektiniu tūriu. Atsizvelgiant
į kiekvienos molekulės savąjį tūrį ![]() . Idealiųjų dujų būsenos lygtyje
. Idealiųjų dujų būsenos lygtyje ![]() molio tūrio Vm
pasiūlė įrasyti
molio tūrio Vm
pasiūlė įrasyti ![]() . Dydis b vadinamas
van der Valso pataisa ir lygus keturgubam molekulės tūriui:
. Dydis b vadinamas
van der Valso pataisa ir lygus keturgubam molekulės tūriui: ![]() . Atsizvelgus į dvi minėtąsias pataisas,
kurių viena susijusi su molekulių laisvuoju tūriu, o kita su
jų traukos jėgomis, gaunama realiųjų dujų būsenos
- van der Valso - lygtis:
. Atsizvelgus į dvi minėtąsias pataisas,
kurių viena susijusi su molekulių laisvuoju tūriu, o kita su
jų traukos jėgomis, gaunama realiųjų dujų būsenos
- van der Valso - lygtis: ![]() . Van der Valso lygtis bet kuriam dujų kiekiui
tokia:
. Van der Valso lygtis bet kuriam dujų kiekiui
tokia: ![]() čia
čia ![]() - molių skaičius, V - dujų tūris.
Van der Valso lygtis yra kūbinė tūrio atzvilgiu lygtis. Kai
v=-mol , ta lygtis tokia:
- molių skaičius, V - dujų tūris.
Van der Valso lygtis yra kūbinė tūrio atzvilgiu lygtis. Kai
v=-mol , ta lygtis tokia: ![]() .
.
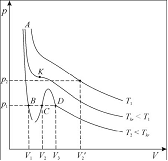
|
Teorinės van der Valso lygties izotermės. Izotermė T = Tkr vadinama krizine |

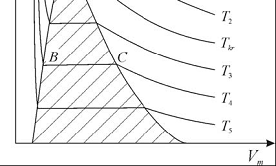
|
Eksperimentinės van der Valso izotermės |
4. Kuo skiriasi kristaliniai ir amorfiniai kietieji kunai?
Kristaliniai turi savo lydymosi temperatura, o amorfiniai neturi apibreztos lyd temp.amorfiniai neturi taisyklingos isorinės formos.kristalinej ir amorfinej busenoj ,kiekvienam atomui kaimynų issidėstymas panasus,tik amorfinej medz tvarka pastebima arti atomo.
5.Ką vadiname faziniu virsmu? Kaip atskirti pirmos rūsies fazinį virsmą nuo antros rūsies fazinio virsmo?
Klapeirono ir Klauzijaus lygtis:![]() čia Q -
medziagos fazinio virsmo siluma: skysčiui garuojant T=const
temperatūroje ji sugeriama, o garams kondensuojantis ji isskiriama.
Kadangi tam tikros masės garų tūris Vg didesnis
uz tokios pat masės skysčio tūrį Vsk,
tai, didėjant temperatūrai, didėja ir fazinio virsmo
slėgis, t.y. dp/dT>0. Klapeirono ir Klauzijaus lygtis tinka visiems pirmosios
rūsies faziniams virsmams, t.y. virsmams, kurių metu sugeriama
arba isskiriama fazinio virsmo siluma (garavimas, lydymasis), suoliskai kinta
sistemos vidinė energija, taigi ir entropija, tankis. Antrosios
rūsies fazinių virsmų metu suoliskai kinta medziagos
savitoji siluma, spūdumas, siluminio plėtimosi koeficientas ir kiti
dydziai.
čia Q -
medziagos fazinio virsmo siluma: skysčiui garuojant T=const
temperatūroje ji sugeriama, o garams kondensuojantis ji isskiriama.
Kadangi tam tikros masės garų tūris Vg didesnis
uz tokios pat masės skysčio tūrį Vsk,
tai, didėjant temperatūrai, didėja ir fazinio virsmo
slėgis, t.y. dp/dT>0. Klapeirono ir Klauzijaus lygtis tinka visiems pirmosios
rūsies faziniams virsmams, t.y. virsmams, kurių metu sugeriama
arba isskiriama fazinio virsmo siluma (garavimas, lydymasis), suoliskai kinta
sistemos vidinė energija, taigi ir entropija, tankis. Antrosios
rūsies fazinių virsmų metu suoliskai kinta medziagos
savitoji siluma, spūdumas, siluminio plėtimosi koeficientas ir kiti
dydziai.
6.Pagal kokius pozymius galima klasifikuoti kietuosius kūnus?
Kietaisiais kunais vadinami tik kristaliniai kunai.Jie skirstomi pagal erdvines gardeles pobudi, ir jos pasikartojima.
![]()
![]()
|