Вла 535i85f 89;тивості розв’язків задачі лінійного програмування формулюються у вигляді чотирьох теорем (доведення теорем та їх наслідки наведено нижче).
Вла 535i85f 89;тивість 1
Вла 535i85f 89;тивість 2 розв’язків. Якщо ж цільова функція набуває екстремального значення
Вла 535i85f 89;тивість 3 A A Ak (k ≤ n) у розкла 535i85f 76;і A x A x Anxn A X
A x A x Akxk A
xj X x x xk
Вла 535i85f 89;тивість 4. (Теорема 2.5) Якщо X = (x1, x2, …, xn) — кутова точка багатогранника розв’язків, то вектори в розкла 535i85f 76;і A1x1 + + A2x2 + … + Anxn = A0, X ≥ 0, що відповідають додатним xj, є лінійно незалежними.
. Необхідно довести, що коли X1 та X2 — плани задачі лінійного програмування (2.1)—(2.3), то їх опукла комбінація X = λ1X1 + λ2X2, λ1 ≥ 0, λ2 ≥ 0, λ1 + λ2 = 1 також є планом задачі.
Так як X1 і X2 — плани задачі, то виконуються такі співвідношення:
AX A X AX A X
Якщо підставити в систему обмежень значення X, то отримаємо:
AX = A( X + λ2X2) = λ1AX1 + λ2AX2 = λ1A0 + λ2A0 = (λ1 + λ2)A0 = A0.
Отримали, що X задовольняє систему обмежень задачі лінійного програмування (2.2), і оскільки Х1 ≥ 0, Х2 ≥ 0, λ1 ≥ 0, λ2 ≥ 0, то й Х ≥ 0, тобто задовольняють і умову (2.3). У такий спосіб доведено, що Х — план задачі лінійного програмування.
 .
Припустимо,
що
багатогранник
розв’язків задачі
обмежений і
має
скінченну
кількість
кутових точок.
Позначимо
його через Q. У
двовимірному
просторі Q має вид
багатокутника,
що зображено
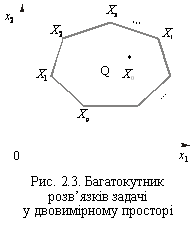
на рис. 2.3. Позначимо
кутові точки
через Х1,
Х2, , Хр, а оптимальний
план — Х0.
.
Припустимо,
що
багатогранник
розв’язків задачі
обмежений і
має
скінченну
кількість
кутових точок.
Позначимо
його через Q. У
двовимірному
просторі Q має вид
багатокутника,
що зображено
на рис. 2.3. Позначимо
кутові точки
через Х1,
Х2, , Хр, а оптимальний
план — Х0.
Задача (2.1) — (2.3) розв’язується на максимум, отже, при будь-якому Х із Q для значення Х0 виконується нерівність F X F X . Якщо Х0 — кутова точка, то перша частина теореми доведена. Припустимо, що Х0 не є кутовою точкою, тоді Х0 є точкою, яка належить опуклій множині (доведено в попередній теоремі). Отже, її можна подати як опуклу лінійну комбінацію кутових точок множини Q, тобто
X = λ1X1 + λ2X2 + … + λpXp,
![]() .
.
У зв’язку з тим, що F(X) — лінійна функція, отримаємо:
![]() (2.16)
(2.16)
У такому
розкла
535i85f 76;і
серед
значень F Xi ![]() вибираємо
найбільше
(припустимо,
що воно відповідає
кутовій
точці
вибираємо
найбільше
(припустимо,
що воно відповідає
кутовій
точці ![]() і
позначимо
його через m, тобто
і
позначимо
його через m, тобто ![]() . Замінимо
в (2.16) кожне
значення F Xi
цим
найбільшим
значенням.
Оскільки
. Замінимо
в (2.16) кожне
значення F Xi
цим
найбільшим
значенням.
Оскільки ![]() , то
, то
![]() .
.
F X F Xk m, а з другого, доведено, що F(X0) ≤ m, значить, F(X0) = m = F(Xk), де Xk — кутова точка. Отже, лінійна функція досягає максимального значення в кутовій точці (Xk).
F X набирає максимальних значень більше, ніж в одній кутовій точці, наприкла 535i85f 76; у точках Х1, Х2, , Хq, (1 ≤ q p , тоді F(X1) = F(X2) = … = F(Xq) = m. Якщо Х опукла лінійна комбінація цих кутових точок, то:
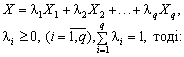
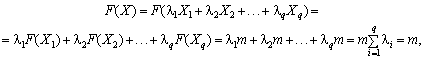
тобто лінійна функція F набирає максимальних значень у довільній точці Х, яка є опуклою лінійною комбінацією кутових точок Х1, Х2, , Хq.
L, де L — достатньо
велике число.
Введення
цього обмеження
означає 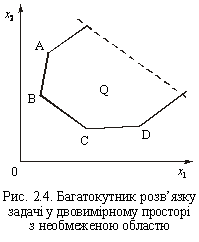 L
L
L. Якщо в одній з них лінійна функція набирає максимального значення, то воно залежить від L. Змінюючи L, значення функціонала можна зробити як завгодно великим, а це означає, що лінійна функція необмежена на багатограннику розв’язків.
Якщо
відомо, що
система
векторів ![]() (k ≤ n) у
розкла
535i85f 76;і
(k ≤ n) у
розкла
535i85f 76;і ![]() ,
, ![]() лінійно
незалежна і
така, що
лінійно
незалежна і
така, що
![]() ,
,
xj X x x xk
![]()
Компоненти векторів Х1 та Х2, значення λ1 і λ2 невід’ємні і останні n – k компонентів вектора Х дорівнюють нулю, тому відповідні n – k компонент векторів Х1 та Х2 також мають дорівнювати нулю, тобто
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
![]() .
.
За
припущенням
вектори ![]() лінійно
незалежні,
тому останнє
співвідношення
виконується,
якщо
лінійно
незалежні,
тому останнє
співвідношення
виконується,
якщо
![]() .
.
Звідси: ![]()
Якщо ![]() —
кутова точка
багатогранника
розв’язків,
то вектори в
розкла
535i85f 76;і
—
кутова точка
багатогранника
розв’язків,
то вектори в
розкла
535i85f 76;і ![]()
![]() ,
, ![]() , що
відповідають
додатним
, що
відповідають
додатним ![]() , є лінійно
незалежними.
, є лінійно
незалежними.
. Не порушуючи загальності, можна вважати нерівними нулю перші k елементів вектора Х, отже,
![]() .
.
Здійснимо
доведення
від
супротивного.
Припустимо,
що система
векторів ![]() лінійно
залежна. Тоді
існують такі числа
лінійно
залежна. Тоді
існують такі числа
![]() , не всі
рівні нулю,
за яких
виконується
співвідношення:
, не всі
рівні нулю,
за яких
виконується
співвідношення:
![]() .
.
![]() .
.
Задамо
деяке число ![]() ,
помножимо на
нього першу
рівність,
далі
результат
спочатку
додамо до другого,
а потім віднімемо
від другого
рівняння:
,
помножимо на
нього першу
рівність,
далі
результат
спочатку
додамо до другого,
а потім віднімемо
від другого
рівняння:
![]() ,
,
![]() .
.
Отже,
система
рівнянь
задачі
лінійного програмування
![]() має
два
розв’язки,
які можуть і
не бути
планами.
має
два
розв’язки,
які можуть і
не бути
планами.
![]()
![]() .
.
> 0,
тому число ![]() можна
вибрати
настільки
малим, що всі
перші
компоненти
можна
вибрати
настільки
малим, що всі
перші
компоненти ![]() та
та ![]() набуватимуть
додатних значень,
тоді
набуватимуть
додатних значень,
тоді ![]() та
та ![]() —
плани. При
цьому
—
плани. При
цьому ![]() , тобто Х — опукла
лінійна
комбінація
точок Х1
та Х2,
що
суперечить
умові теореми,
оскільки Х — кутова
точка.
, тобто Х — опукла
лінійна
комбінація
точок Х1
та Х2,
що
суперечить
умові теореми,
оскільки Х — кутова
точка.
Припущення
стосовно
лінійної
залежності
векторів ![]() привело
до
суперечності.
Отже, воно є
неправильним,
а система
векторів —
лінійно
незалежна.
привело
до
суперечності.
Отже, воно є
неправильним,
а система
векторів —
лінійно
незалежна.
. Оскільки
вектори ![]() мають
розмірність m, то
кутова точка
багатокутника
розв’язків має
не більше,
ніж m
додатних
компонентів
мають
розмірність m, то
кутова точка
багатокутника
розв’язків має
не більше,
ніж m
додатних
компонентів ![]() .
.
. Кожній
кутовій
точці
багатокутника
розв’язків
відповідає ![]() лінійно
незалежних
векторів
системи
лінійно
незалежних
векторів
системи ![]() .
.
|