CURS 10

Derivate. Functii derivabile

Fie f o functie pe un interval I si un punct din I.

Definitie: Se spune ca functia este derivabila în punctual daca raportul

are în punctul limita finita. Limita însasi se numeste derivate functiei f in punctul si se noteaza :

se citeste derivata functiei f în raport cu x în punctul .

In loc de se mai folosesc pentru derivata si notatiile:

Daca limita exista, insa este infinita (+ ∞ sau - ∞) spunem ca derivata functiei din punctul este infinita. În aceasta situatie însa, functia nu este derivabila în punctul .

Observatii

Functia trebuie sa fie definita in punctual . Daca o functie nu este definita într-un punct, nu se pune problema derivabilitatii în acel punct.

Derivata într-un punct este un numar.

Teorema Daca functia este derivabila în punctual atunci f este continua în punctul .

Demonstratie: Pentru , avem egalitatea:

si

de unde rezulta ca are limita în punctul pe .

Întradevar:

deci este continua în punctul .

Interpretarea geometrica a derivatei

Fig.1

Fie si graficul functiei f pentru : , care este un arc de curba plana. Daca este un punct în care functia f este derivabila, iar x un punct oarecare din interval, conform figurii alaturate avem din triunghiul M₀MN.: (1), unde este coeficientul unghiular al secantei M₀M. Daca punctul , secanta M₀M se apropie ca pozitie de dreapta M₀Q, tangenta la grafic în punctul M₀ (daca graficul are o tangenta unica în punctul M₀), deci: . Deci derivata functiei , într-un punct este egala cu tangenta trigonometrica a unghiului pe care îl face tangenta la grafic în punctul cu axa 0X. Daca derivata este infinita (+∞ sau -∞), , dreapta M₀Q este paralela cu axa 0Y. Daca raportul (1) nu are limita, graficul nu are tangenta unica în punctul M₀ (punct unghiular) sau tangenta nu exista.

Interpretarea cinematica a derivatei

Fie M un punct mobil care descrie axa 0X. La fiecare moment t drumul parcurs pe axa este o functie care ne da legea de miscare a punctului. Punctul se misca uniform daca legea de miscare este data de relatia liniara în t:

, constante

Spatiul parcurs între doua momente oarecare t₁ < t₂ este

si raportul

se numeste viteza punctului M în miscare rectilinie si uniforma. Deci într-o miscare rectilinie si uniforma viteza este constanta. Fie acum o miscare oarecare a punctului M pe axa 0X, miscare data de legea x(t), si sa consideram doua momente t₁, t_2, precum si raportul (1). Daca substituim miscarile date, în intervalul (t₁, t₂) o miscare uniforma a unui alt punct, care coincide cu punctul M la timpul t₁ si t₂ raportul (1) poate fi considerat ca viteza medie a punctului M în intervalul de timp (t₁, t₂) si el ne da o caracterizare a miscarii între aceste momente, caracterizare care va fi cu atât mai buna cu cât intervalul (t₁, t₂) este mai mic. Astfel putem considera limita vitezei medii când adica: . Daca aceasta limita exista si este finita, ea este prin definitie viteza punctului M la momentul t₁, deci: .

Functii derivabile pe un interval

Definitie

Se spune ca functia este derivabila pe I daca este derivabila in fiecare punct . Functia care face ca fiecarui punct sa-i corespunda derivata functiei în punctul x, se numeste functia derivata a functiei f sau, mai simplu, derivata lui f si se noteaza: f', sau Df. Cu ajutorul acestor relatii, derivata functiei într-un punct se mai scrie: .

Derivata la stânga. Derivata la dreapta.

Definitie

Fie functia si . Se spune ca functia f este derivabila la dreapta în punctul x₀ daca raportul are limita la dreapta finita, în punctul x₀. Aceasta limita se numeste derivata la dreapta a functiei f în punctul x₀ si se noteaza : .

Definitie

Fie functia si . Se spune ca functia f este derivabila la stânga în punctul daca raportul are limita la stânga finita, în punctul . Aceasta limita se numeste derivata la stânga a functiei f în punctul x₀ si se noteaza : .

Observatii

1. Din definitie rezulta ca o functie este derivabila într-un punct daca este derivabila la dreapta si la stânga în punctul si daca cele doua derivate (numite derivate laterale) sunt egale: .
2. Pentru o functie definita pe un interval compact (închis si marginit [a, b] ) are sens problema derivatei în orice punct din interval. În punctul a are sens problema derivatei la dreapta, iar în punctul b are sens problema derivatei la stânga.
3. Daca derivata la dreapta (sau la stânga) a unei functii f într-un punct este infinita (+ ∞ sau - ∞), functia nu este derivabila la dreapta (sau la stânga) în punctul .

Interpretarea geometrica a derivatei la dreapta si a derivatei la stânga.

a)      O functie este derivabila la dreapta în punctul daca:

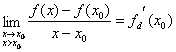. Prin urmare, conform figurii urmatoare,

semidreapta M₀M, când (M la dreapta lui M₀), se apropie ca pozitie

de semitangenta la dreapta în punctul M₀, M₀Q. Coeficientul unghiular al semidreptei M₀Q este .

Fig. 1

Daca = + ∞, semitangenta M Q este paralela cu axa 0Y si este situata deasupra punctului M₀ (conform figurii 2).

Fig. 2

Daca = - ∞, semidreapta M Q semitangenta la grafic în punctul , este paralela cu axa 0Y si este situata sub punctul M.

b)      O functie este derivabila la stânga în punctul daca 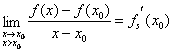. Prin urmare (conform figurii 3) semidreapta

Fig. 3

M₀M când (M la stânga lui M₀) se apropie ca pozitie de semitangenta la stânga în punctul M₀, M₀Q. Coeficientul unghiular al semidreptei M₀Q este . Daca = + ∞, semitangenta M Q este paralela cu axa 0Y si este situata sub punctul M₀ (conform figurii 4). Daca = - ∞, semitangenta M₀Q este paralela cu axa 0Y si este situata deasupra punctului M

Fig. 4

c)      Daca functia f are în punctul derivatele laterale diferite si cel putin una din ele este finita, punctul se numeste punct unghiular al graficului functiei , iar cele doua semitangente fac între ele un unghi si (conform figurii 5).

Fig. 5

d)      Daca functia f are în punctul derivatele laterale infinite si egale, cele doua semitangente sunt în prelungire punctul x este un punct de inflexiune al graficului functiei (conform figurii 6).

Fig. 6

e)      Daca functia f are în punctul derivatele laterale infinite si diferite = = - ∞ sau = = + ∞, cele doua semitangente se suprapun; punctul se numeste punct de întoarcere al graficului functiei (conform figurii 7).

Fig. 7

Reguli de derivare.

Operatii cu functii derivabile.

Teorema 1

Daca functiile sunt derivabile într-un punct , atunci functia este derivabila în punctul si:

.

Demonstratie

si pentru ca f si g sunt derivabile în punctul , avem:

(1), deci

(2).

Observatii

1. Teorema ramâne adevarata pentru suma unui numar finit de functii derivabile f₁, f₂, ..... f_n într-un punct , si anume

2. Regula (2) ramâne adevarata si în cazul când derivatele si sunt infinite, cu conditia ca suma sa aiba sens.

Consecinta

Daca functiile si sunt derivabile pe I, atunci suma este derivabila pe I si: .

Teorema 2

Daca functiile sunt derivabile într-un punct , atunci functia este derivabila în punctul si:

.

Demonstratie

Avem

si pentru ca sunt derivabile în punctul , obtinem:

(3).

Observatie

1. Regula (3) ramâne valabila si în cazul când derivatele si sunt infinite, cu conditia ca diferenta sa aiba sens.

Consecinta

Daca functiile si sunt derivabile pe I, atunci diferenta este derivabila pe I si: .

Teorema 3

Daca functiile sunt derivabile într-un punct , atunci functia este derivabila în punctul si:

.

Demonstratie

Pentru din I avem:

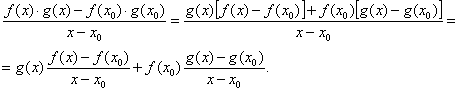
Prin ipoteza, functiile f si g sunt derivabile în punctul , deci

sunt continue în punctul prin urmare si , astfel încât putem scrie:

adica (4).

Daca sunt n functii derivabile în punctul x₀ , produsul lor este derivabil în punctul si:

(5)

Demonstratie

Pentru n 2 formula este adevarata, deoarece este formula (4). Presupunem ca este adevarata pentru n-1 sa aratam ca este adevarata si pentru n:

care este tocmai formula (5).

În particular, daca atunci .

Consecinta: Daca functiile sunt derivabile pe intervalul I, atunci functia este derivabila pe I si:

.

Teorema 4

Daca functiile sunt derivabile într-un punct , atunci functia este derivabila în punctul si:

.

Demonstratie Functia g(x) ia în punctul x₀ valoare diferita de 0; deoarece este continua in punctul x₀, exista o vecinatate V a lui x₀ în care . Pentru avem:

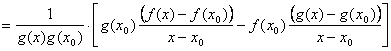, însa

deci avem la limita:

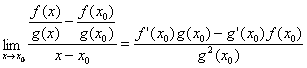adica:

.

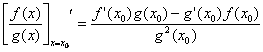Consecinta: Daca functiile sunt derivabile pe I si , atunci este derivabila pe I si:

.

Derivabilitatea functiilor compuse.

Sa consideram functia , cu domeniul valorilor I si functia ; pentru functia compusa avem urmatoarea

Teorema: Daca functia este derivabila în punctul si functia este derivabila este derivabila în punctul corespunzator atunci functia compusa este derivabila in punctul si

.

Demonstratie

Functia u fiind derivabila în punctul x₀, avem:

(1). Functia f(u) fiind derivabila în punctul u₀, avem: ; înainte de a trece la limita, putem scrie:

cu (3).

Functia data de (2), cu , este continua în punctul . Întradevar, 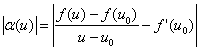si pentru , avem deoarece f(u) este derivabila în punctul u₀. Derivabilitatea functiei F(x) este:

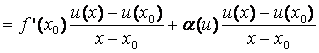. Deci la limita avem:

si daca tinem seama de (1) si (3) avem: .

Consecinta Daca functia este derivabila pe I si functia f este derivabila pe I atunci functia compusa este derivabila pe I si: .

Derivabilitatea functiilor inverse

Teorema Fie functia , care se poate inversa pe I. Daca f(x) este derivabila în punctul , atunci functia sa inversa este derivabila în punctul si (1).

Demonstratie

Am aratat ca functia este continua pe J; ramâne sa mai aratam ca pentru orice sir (y_n) cu avem: 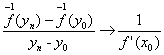. Functia f fiind biunivoca, la corespunde un x_n astfel încât y_n=f(x_n), deci , astfel încât: 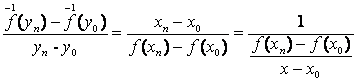, si la limita, deoarece sirul (y_n) este arbitrar, avem:

.

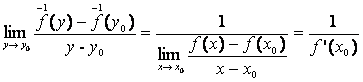Consecinta daca functia , este derivabila pe I si , atunci functia inversa este derivabila pe si

Observatii

1. Am aratat ca functiile au graficele simetrice fata de prima bisectoare a axelor. Relatia dintre derivatele lor în punctele corespunzatoare: confirma acest fapt, anume ca tangentele la cele doua curbe în punctele sunt asimetrice fata de prima bisectoare.
2. Daca , relatia (1) se mentine, anume derivata functiei inverse este infinita. Mai precis, daca f(x) este strict crescatoare, deoarece pentru orice si daca f(x) este strict descrescatoare deoarece pentru orice .

Derivatele functiilor trigonometrice

a)      Functia este derivabila pe domeniul de definitie R. Avem:

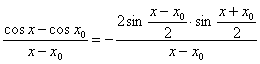
, deci

.

Consecinta Daca este derivabila, functia este derivabila pe I si: .

b)      Functia este derivabila pe domeniul de definitie R. Deoarece , folosind regula de derivare a functiilor compuse, precum si rezultatul precedent:

c)      Functia este derivabila pe domeniul Pentru avem: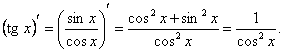

d)      Functia este derivabila pe domeniul Pentru ,

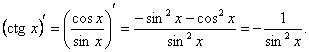
Derivata functiei logaritmice

Functia este derivabila pe tot domeniul de definitie . Avem: 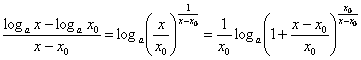, deci 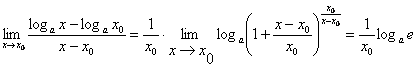, deoarece Din formula rezulta ca .

Observatie Daca .

Derivata functiei exponentiale

Functia este derivabila pe tot domeniul de definitie . Functia este inversa functiei logaritmice .

Asadar .

Observatii

Daca .

Daca u(x) definita pe I este derivabila pe I, atunci .

Functii hiperbolice

Functia , numita ,,sinus hiperbolic", se defineste cu ajutorul functiei exponentiale în modul urmator: . Domeniul valorilor este . Functia este o functie impara, deoarece . Graficul este simetric fata de originea axelor (conf. fig. (1)), .

Fig. 1

Functia , numita ,,cosinus hiperbolic", este definita de . Domeniul valorilor este . Functia este o functie para, deoarece . Graficul este simetric fata de axa 0Y (conf. fig. (2)). Graficul functiei se numeste si ,,curba lantisor". Curba da pozitia de echilibru a unui fir omogen, flexibil, inextensibil, supus la actiunea gravitatiei si ale carui capete sunt fixate (A, B), .

Fig. 2

Functia , numita ,,tangenta hiperbolica" (conf. fig. (3)), este definita de .

Fig. 3

Functia , numita ,,cotangenta hiperbolica" (conf. fig. (4)), este definita de .

Fig. 4

Proprietatile functiilor hiperbolice

Functiile hiperbolice au proprietati care le apropie de functiile circulare. Dam câteva dintre ele

1. 
2. 
3. 
4. 
5. 

Toate se dovedesc înlocuind functiile hiperbolice cu expresiile lor în functie de exponentiale. Astfel, pentru 1 avem

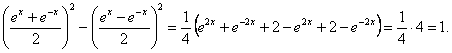
Derivatele functiilor hiperbolice

a)      Functia este derivabila pe domeniul de definitie R. ; .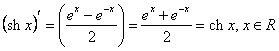

b)      Functia este derivabila pe domeniul de definitie R. ; .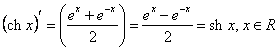

c)      Functia este derivabila pe domeniul de definitie R. ; .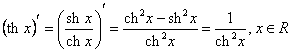

d)      Functia c este derivabila pe domeniul de definitie R-. ; .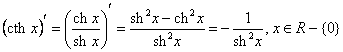

Derivatele functiilor circulare inverse

Functia arcsin x, definita pe [-1, +1], este derivabila pe (-1, +1): , deci . În punctele +1 sau -1, arcsin x are derivata +

Functia arccos x, definita pe [-1, +1], este derivabila pe (-1, +1): , deci . În punctele +1 sau -1, arcsin x are derivata -

Functia arctg x, definita pe ), este derivabila pe domeniul de definitie: , deci .

Functia arcctg x, definita pe ), este derivabila pe domeniul de definitie: , deci .

Functii hiperbolice inverse

a)      Functia este strict monotona pe tot domeniul sau de definitie R. Avem sau . Solutia care convine este . Schimbând pe y în x dupa logaritmare, obtinem functia inversa a functiei : , numita ,,argument sinus hiperbolic". Functia este derivabila pe domeniul de definitie

.

b)      Functia este strict monotona pe intervalele . Avem sau . Schimbând pe y cu x, obtinem functia inversa a functiei numai pentru ramura monotona definita pe : , numita ,,argument cosinus hiperbolic"; pentru ramura din intervalul avem: .

c)      Functia este strict monotona pe multimea de definitie. Avem sau , numita ,,argument tangenta hiperbolica". Functia este derivabila pe domeniul de definitie: .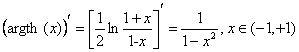

d)      Functia , este monotona pe intervalele . Avem: . Schimbând pe x cu y, obtinem functia inversa a functiei , pentru ramura monotona definita pe , numita ,,argument cotangenta hiperbolica"; pentru ramura din intervalul avem .