Eroarea teoretica a mediei aritmetice

SUBIECTUL NR 11:

PARAMETRII IMPRASTIERII (amplitudinea "a", Dispersia empirica ; abaterea standart empirica.

Valoare empirica= valoarea calculabila.

n- mare dar finit si repr nr. de determinari. Împreăstierea este un al V-lea obiectiv al Statisticii Matematice. În TPD, notiunea e similară cu precizia măsurătorilor.

Cele 2 probeleme mari sunt:

determinarea celei mai bune marimi ( marimea in care sa aveam cea mai mare incredere dintr-un sir de determinari) In TPD, geodezie, topografie se foloseste media aritmetica.

Determinarea preciziei sirului de determinari

-erorile sunt repartizate in jurul marimii centrale

Imprastierea se refera la diferente fata de tendinta centrala. Cu cat masuratorile sunt mai apropiate de media aritm 12112j914m etica cu atat sunt mai bune.

Amplitudinea "a"

(1)

a= 0.015 m (2)

Cu cat "a" e mai mare cu atat masuratorile sunt mai putin precise( mai imprastiate)

Dispersia:

Se presupune ca avem sirul de masuratori:

si se cunoaste media teoretica ""

eroarea= marimea masurata () - marimea de referinta. (4)Putem avea multe valori de referinta. Daca valoarea teoretica este marimea de referinta a erorii reale ε.

Daca marimea de referinta e media aritmetica eroarea se mai numeste si eroare aparenta notata cu e.

In general se lucreaza cu corectiile aparente "v" unde v=-e.

Presupunem ca aveam si prin prin aplicarea formulei 4 obtinem:

(5)

Definitie: Prin definitia data de Gauss, dispersia notata cu poate fi scrisa in diferite moduri:

D (x⁰) = (6)

si numai partea pozitiva s.n. abatere standart empirica.

Adunam ecuatia 5 pe verticala si adunam ecuatia Gauss.

Media aritmetica:

Valoarea de referinta a erorii teoretice

SUB.12

Eroarea teoretica a mediei aritmetice.

;;

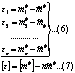
ε-eroei reale

ε poseda caracteristicile principale ale eroarilor intamplatoare:

a.Er. sunt mici

b.Cele pozitive sunt aproximativ egale numeric cu er. reala negativa.

.(14) din cauza ca sunt eroari ce apartin numerelor reale.

;

(17) face legatura dintre ecuatia reala a mediei aritmetice si abaterea standart

Erorile reale sunt in general necunoscute, deoarece acestea se raporteaza la... Care de asemenea raman o medie necunoscuta. Din acest motiv in TPD , Geodezie si Topografie se lucreaza cu erori aparente "e=-v" v- fiind corectua aparenta. Deoarece acestea au ca marime de referinta media aritmetica care se poate determina.

SUB .13 Utilizarea corectiilor aparente "v" pt. determinarea dispersiei empirice "" si abaterii standard empirice ""

- eroarea reala a mediei aritmetice la patrat

Erorile "R" ε nu se pot determina, deoarece au ca marime de referinta media teoretica (n→ ∞)

În practica se folosesc erorile aparente "e", deoarce au ca marime de referinta media aritmetica (n=finit)

De obicei nu lucram cu erori aparente "e", ci cu corectiile "v" care sunt egale numeric cu "e" dar de sens contrar.

Avem in vedere acest sir de masuratori:

si putem defini erorile reale (in raport cu m0)

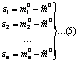
Si introducem erorile aparente

,

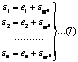
.(1)

Abaterea standard "s_o" e determinata în TPD dupa traditia th erorilor si metoda celor mai mici patrate s. n. eroarea medie. Dispersia "s₀²" s.n. varianta.

Notiuni finale1.Raportul dintre abaterea standard a unei singure mas. "s₀" si er. medie probabila a unei singure mas. Es s₀/E_s≈3/2)

2) Toleranta pt un sir de mas. dat (T≈3s₀)Δ_max=m₀^max-m₀^min

Masurat. sunt corecte când Δ_max<Toleranta

3)Abaterea standard empirica a mediei aritmetice

4) Raportul de eficacitate (raportul dintre abaterea standard empirica a mediei aritmetice si abaterea standard empirica a unei singure masuratori)

SUB. 14.Principiul celor mai mici patrate

(1)- Probabilitatea infinitezimala de producere a unui evaniment în intervalul (x, x)

h-ct. de precizie

C-const.(2)- Probab. ca 2 evenim.A si B sa se produca simultan si în acelasi timp, evenim. sa fie independente

Daca 2 evenim. A si B sunt independente si se produc simultan, probab. " lor este egala cu produsul probabilitatilor individuale. în domeniul teoretic

a) d ;d - infinit mica ; - finit mica

b) Ponderile even. sunt între ele, masurat. sunt de aceeasi precizie

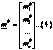
c) (3) trecem de la erorile "x" la corectia "v"

v=-x (6)

d) Din aceste ipoteze, evenim. din (4) vor avea probabilitatile finit mici egale între ele

(8)

În ipoteza ca evenimentele sunt independente se produc simultan, probab. intersectia lor este data de formula

ΔP max, trebuie ca numitorul sa fie minim

[vv]Gauss-masuratori de aceeasi precizie

[vv]Metoda celor mai mici patrate

h- parametru de precizie

h-este egala cu ordonata la origine (la Curba clopot Gauss)

Masuratori de prec. diferite (masuratori ponderate)

[pvv]- principiul metodei celor mai mici patrate.

SUB.15Covarianta, corelatii statistice

E-operatorul mediei th (mathematic: speranta matem. sau valoarea de asteptare)

M-operatorul mediei aritmetice

-media th. a sirului de masuratori din

-media aritmetica din acelasi sir

-M(m⁰) (1')

_I -erori reale

eroarea=marimea masurata-marimea de referinta 

ε _I este dedusa în ipoteza în care se cunoaste media teoretica

e_i=m_i⁰- (2')

(3) → varianta masuratorii

(4) → varianta unei singure masuratori din sirul (6)

→ generalizeaza formula si se num. matrice de varianta-covarianta

De la acest sir plecam cu ipoteza ca avem 2 siruri de masuratori.

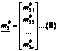
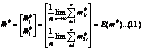
Nota În formulele de pâna acum s-a presupus ca sirul si (2), (8) contin acelasi "n" de masuratori. În ipoteza ca se stiu mediile teoretice se pot calcula erorile teoretice.

În analogie cu definitia (3), definim matricea de varianta notata ""

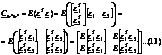
(14)si (15) sunt variantele masuratorilor avute in vedere

In formula (13) sunt alti termeni

Covarianta σ₁₂ se refera întotdeuna la 2 siruri de masuratori efectuate asupra unei marimi de acelasi nr. de ori

;

Covarianta se exprima si mai clar daca se introduce o noua notiune si anume "ρ₁₂"-coeficient th. de corelatie.

În practica nu se pot determina mediile th. si ₀² (definite în relatia (11)), atunci lucram cu mediile aritmetice si Nu lucram cu variantele σ₀₁², σ ₀₂², ci cu variatiile empirice.

În loc de covarianta th. σ₁₂ trecem la covarianta empirica.

Analog cu (18):

se poate calcula:

Coeficientii de corelatie th, empirici exprima legatura statistica (stochastica) între cele 2 siruri de masuratori m⁰₁, m⁰₂. Cu cât acesti coeficienti sunt mai mari (în valoare absoluta), cu atât se exprima o dependenta mai mare între cele 2 siruri de masuratori.

Valorile extreme +-1 sunt specifice pt situatia în care exista egalitatea

Nota: Masuratorile sunt independente statistic atunci când

Relatia (26) este imposibil de pus in practica.