CAPITOLUL III-ROUGH SET (MULTIMI DIFUZE)

Rough-set: starea actuala si dezvoltari viitoare

Filosofia: filosofia multimilor difuze (Rough Set) contine ideea de clasificare. Orice organism viu sau robot (agent), pentru a se comporta rational în realitatea exterioara trebuie sa aiba abilitatea de a clasifica obiecte reale sau abstracte (de exemplu semnale senzoriale). Pentru a face o clasificare, este necesar sa se ignore unele diferente între obiecte, astfel formând clase de obiecte care nu sunt semnificativ diferite. Aceste clase de elemente indecelabil diferite pot fi privite ca elemente constructive de baza (concepte) folosite pentru constructia unui sistem de cunostinte despre realitate. De exemplu, daca obiectele clasificate sunt grupate dupa culoare, atunci clasa tuturor obiectelor identificate ca fiind rosii formeaza conceptul de "rosu". De aici presupunerea noastra ca orice agent este echipat cu mecanisme de clasificare variate si cu concepte elementare cu aceste clasificari, formând cunoasterea sa fundamentala despre lume si sine.

De aceea cunoasterea din punctul de vedere al acestei abordari poate fi definita ca o abilitate de clasifica. De acum putem reprezenta formal cunoasterea ca o familie de partitii ale unui univers fixat (definit), sau din acelasi punct de vedere matematic sub forma unei familii de relatii de echivalenta.

Perspectiva prezentata a cunoasterii e de natura semantica, în care granularitatea cunostintelor (existenta elementelor indecelabil diferite) este de prima importanta în opozitie cu raspândita definitie sintactica a cunoasterii în care aspectele formale ale acesteia sunt luate ca punct de plecare pentru definitie. Aceasta poate fi reformulata afirmând ca în teoria multimilor difuze (Rough Set) datele au mai mare importanta decât limbajul.

Cea mai importanta conceptie din teoria Rough Set este ideea cunoasterii imprecise. Cunoasterea este imprecisa daca ea contine elemente imprecise.

Conceptele imprecise pot fi definite prin contrast cu cele exacte ca fiind acelea care nu au o separare clara a elementelor interioare de cele exterioare, cum au conceptele precise (crisp concepts). Astfel un concept imprecis poate fi definit cu ajutorul a doua concepte precise: aproximarea superioara si aproximarea inferioara, însemnând totalitatea obiectelor care apartin sigur conceptului, respectiv multimea obiectelor care pot apartine conceptului. Diferenta între aceste doua aproximari este o regiune de frontiera a conceptului, continând toate obiectele care nu pot fi clasificate cu certitudine ca apartinând conceptului sau complementului sau (i.e. exteriorului sau) folosind cunoasterea disponibila.

Aceasta perspectiva asupra conceptelor vagi poate fi atribuita lui Frege, care scrie:

"Conceptul trebuie sa aiba o frontiera clara. Unui concept fara frontiera clara i-ar corespunde o zona care nu are frontiera clara de jur împrejur."

Ideea de aproximare este baza în teoria Rough Set.

AI - Aproximarea inferioara a unui concept consta în toate obiectele care apartin sigur conceptului.

AS - Aproximarea superioara a unui concept consta în toate obiectele care ar putea apartine conceptului.

Diferenta dintre AI si AS e regiunea de frontiera a conceptului si consta în toate obiectele care nu pot fi clasificate cu certitudine din punctul de vedere al conceptului folosind cunoasterea obisnuita. Ideea aproximarilor e unealta fundamentala în teoria multimilor difuze.

Pentru a reprezenta clasificarile vom folosi conceptul de sistem de informatie SI. Formal sI e o pereche S = (U, A) unde U = multime finita nevida de obiecte (univers) si A = multime finita de atribute. Fiecarui atribut i se asociaza o multime a valorilor sale V_a, care este domeniul atributului "a". Fiecare atribut a A e o functie a : U V_a care asociaza fiecarui obiect x U o valoare atributiva unica din V_a. Fiecare submultime de atribute B A defineste unic o relatie de echivalenta

IND(B) = .

De obicei U/IND(B) (multime cât sau multimea c 121k109b laselor de echivalenta) este clasificarea corespunzatoare lui IND(B).

AI a lui X U functie de B e o reuniune de clase de echivalenta a IND(B) care e inclusa în X sau formal:

X =

AS a lui X U functie de B e reuniunea tuturor claselor de echivalenta a IND(B) care are intersectia nevida cu X adica:

X =

Regiunea liniei de frontiera e definita ca BN_B(x) = x - x si va fi numita B-frontiera lui X.

Multimea X reprezinta toate elementele lui U care pot fi clasificate cu certitudine ca elementele lui X folosind cunoasterea B.

Multimea X reprezinta toate elementele posibile ale lui X folosind multimea atributelor B.

Multimea BN_B(x) e multimea tuturor elementelor care nu pot fi clasificate nici ca x, nici ca -x prin atributele din B.

Def. Spunem ca o multime e difuza cu privire la B daca X X, altfel multimea e exacta.

Astfel o multime e difuza daca nu are frontiera bine definita, adica nu poate fi unic definita folosind cunoasterea disponibila.

Pentru aplicatii practice avem nevoie de caracterizarea termenului difuzitate ca:

numit masura a preciziei, X F a_B(x) " B, X U.

Daca a_B(x) = 1 regiunea de B-frontiera a lui X e vida si multimea X e definita în cunoasterea B.

Daca a_B(x) < 1regiunea de B-frontiera a lui X e nevida si multimea X nu e definibila în cunoasterea B.

Aproximarea multimilor e unealta fundamentala în conceptia multimilor difuze si e folosita pentru a aproxima descrierea unor concepte (submultimi ale universului U) cu ajutorul atributelor.

Pornind de la conceptul de clasificare putem defini o varietate de alte notiuni fundamentale pentru filosofia multimilor difuze si aplicatii necesare pentru a descoperi relatii între atribute si obiecte. Cele mai importante probleme ce trebuie analizate sunt dependenta atributelor (relatiile cauza - efect), surplusul atributelor si generarea regulii de decizie.

Principalele probleme vizate de teoria multimii difuze în aplicatii sunt:

analiza datelor

o       descoperirea dependentelor de date

o       semnificatia datelor

o       generarea algoritmilor de decizie ai datelor

o       clasificarea aproximativa a datelor

o       descoperirea asemanarilor si deosebirilor între date

analiza cunoasterii

reprezentarea cunoasterii imprecise

procesarea imaginii - folosind concepte de baza ale teoriei multimilor difuze se pot dezvolta usor multi algoritmi primari pentru procesarea imaginii si recunoasterea caracterelor, ca de exemplu algoritmii de subtiere si cei de gasire a conturului.

Aplicatiile multimilor difuze pot fi împartite în mai multe grupe care au câteva trasaturi comune:

Clasificari aproximative. În aceasta grupa, multimile difuze pot fi folosite la crearea algoritmilor ce furnizeaza date, descoperirea asemanarilor sau diferentelor în seturi de date, descoperirea de tipare în seturi de date.

Sinteza circuitelor. Multimile difuze ofera metode alternative în minimalizare, gasirea greselilor (aceasta metoda e în strânsa legatura cu metodele booleane).

Mecanism de învatare. De obicei în literatura cu privire la inteligenta artificiala este denumita ca "a învata din exemple": se considera un singur element, din analiza caruia sa rezulte o caracterizare completa si complexa a universului. Se pare ca teoria multimilor difuze se preteaza acestui mecanism de învatare.

Exemple de multimi difuze

Exemplul 1

Acest exemplu are rolul de a arata modul de generare al unei multimi difuze. Patratul alaturat reprezinta spatiul de aproximare. Exista doua atribute corespunzatoare celor doua dimensiuni. Primul atribut are 5 valori, iar al doilea are 6 valori.

Exemplul 2

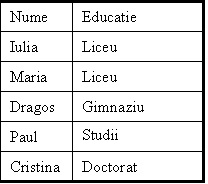
Fie Universul caracterizat prin tabela alaturata pentru care trebuie sa gasim multimea X a celor cu sanse pentru o slujba buna

si pentru care se defineste multimea de atribute A =

este multimea claselor de echivalenta

reprezinta aproximarea inferioara (regiunea pozitiva) iar

reprezinta aproximatia superioara

Rezulta ca reprezinta regiunea negativa iar
este frontiera

Rezultatul aproximarii este prezentat in tabelul urmator

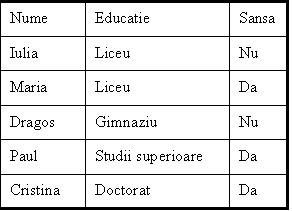
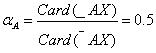
increderea in aproximarea facuta este de 50%

Determinarea OI a operatorilor logici difuzi

Fiind bazata pe teoria multimilor difuze, aceasta lucrare stabileste spatiul de operare [ξ+,ξ*]. Este de asemenea o submultime a intervalului de valori adevarate [0,1]. Operatorul este pus in fata formulelor pentru a da nastere logicii multivalorice numita operator al logicii difuze ORL (operator rough logic). Defineste validitatea OI, inconsistenta (incompatibilitatea) OI, determinarea OI, unde OI este abrevierea de la interval operator (Operator Interval). De asemenea demonstreaza teorema de acuratete a demonstratiei logice.

Notiuni in ORL

Fie U o multime nevida si R o relatie de echivalenta pe U.

Daca este o submultime a lui U, atunci multimea de aproximare inferioara }, multimea de aproximare superioara , unde R(x) este o clasa care il include pe x.

Proprietatile aproximarilor superioare si inferioare sunt date de: si , unde cardS reprezinta cardinalul lui S care este limitat ca finit, evident .

Proprietatile aproximarilor superioare si inferioarea si sunt construite ca intervalul de operare [,]. Evident, este o submultime din [0,1].

Definitia 1

Fie operatorii, valoarea adevarului ale formulelor in ORL. Atunci:

operatia de compunere a operatorilor

operatia de negare a valorilor adevarate

Definitia 2

Fie P un simbol predicativ n-dimensional, un operator, P(x₁, ....., x_n) un atom de logica de ordin I FOL (first order logic), atunci ξP este un atom difuz al ORL.

Definitia 3

Fie un operator difuz, atunci formulele ORL sunt definite recursiv astfel:

atomul ORL este o formula in ORL

daca W si W₁ sunt formule in ORL, atunci sunt formule in ORL

daca W este o formula in ORL , x este o variabila libera in W, atunci si sunt formule in ORL

formulele care se pot obtine din (1)-(3) sunt formule in ORL

Definitia 4

Fie A=(U,R) un spatiu de aproximare, I_R si u_R interpretari difuze ale formulelor si distributii difuze ale variabilelor individuale in formulele din ORL. Termenul de distributie T_IruR care corespunde cu I_R si u_R reprezinta o harta de la termeni la obiecte atunci

daca termenul este simbolul constant al unui obiect din W, atunci , unde e este o entitate

daca termenul este un simbol variabil care are loc in W, atunci , unde c este o constanta din U

daca termenul este o functie de spatiu n, a formei , unde g este o harta de la Uⁿ la U

daca termenul este un predicat n dimensional al formei , si , atunci , unde P este o relatie pe U

Prezicerile care au loc in formule ale logicii sunt vazute ca relatii. Pentru orice relatie R, am putea afla aproximarea inferioara si aproximarea superioara in raport cu R. De aceea valorile afirmative ale formulelor din ORL pot fi determinate de formule matematice.

Valoarea afirmativa a unei formule, T_IruR(W) este determinata in mod unic cu ajutorul definitiei urmatoare.

Definitia 5

Fie W si W₁, formule in ORL, I_R si u_R sunt interpretarea respectiv distributia formulelor atunci

(1)

(2)

(3)

(4)

(5)

unde si U sunt limitate ca finite.

Determinarea OI in ORL

Valorile de adevar ale formulelor se gasesc in intervalul [0,1]. Determinarile ORL in rapor cu multimea de operare [,] se numesc determinari OI ale ORL.

Definitia 6

Fie [,] o multime de operare, [0,1] multimea de valori adevarate ale formulelor in ORL, daca

si ,

atunci W se numeste [,] - valid, scris pe scurt OI - valid;

atunci ~W se numeste [,] - neconsistent (sau invalid), scris pe scurt OI - invalid.

Pentru orice formula din FOL, exista o multime de clauze (cerinte) care este echivalenta cu formula originala prin faptul ca formula poate fi satisfacuta daca multimea corespunzatoare de clauze poate fi satisfacuta.

Propozitie

O formula din ORL, W poate fi transformata intr-o forma normala conjunctiva CNF (Conjunctive Normal Form)

unde si fiecare c_i, i=1,...,m este o disjunctie.

Definitia 7

Fie un operator, atunci si sunt realitati in ORL. Primul este o realitate de pozitie, iar al doilea o negatie a realitatii.

Definitia 8

Fie si , atunci si este o pereche complementara de realitati in raport cu din ORL, pe scurt scris OI - complementara a realitatii. Si daca , unde =_R este un semn de echivalenta difuza in raport cu eroarea θ, atunci ξL si ξ₁L se numesc realitati similare sau mai pe scurt OI - realitati similare.

Operatorul ξ poate fi cel mult limitat sa se mute in interior, inaintea predicatelor si sa nu aiba nici o legatura cu variabilele individuale sau parti din interiorul predicatului, deoarece algoritmul de unificare in ORL e similar cu cel din FOL.

Definitia 9

Fie C₁ si C₂ , doua clauze fara variabile individuale in comun in ORL, ξ₁L₁, ξ₂L₂ doua siruri de caractere in C₁ respectiv C₂. Daca C₁ si C₂ au un unificator cel mai general mgu (most general unifier) σ in algoritmul FOL, si si este o pereche complementara de siruri de caractere, unde "ο" este un semn de operare al compozitiei de substitutie, atunci clauza se numeste rezolvantul binar al lui C₁ si C₂ in ORL, desemnat de OI(C₁, C₂), unde este o multime de siruri de caractereOI similare in C_i.

Determinarea este puternica prin aceea ca oricare clauza care poate fi derivata dintr-un set de clauze ce utilizeaza determinarea, este implicata logic de acel set de clauze in FOL. Astfel, ajungem la urmatoarea teorema in ORL a determinarii puternice in OI.

Teorema

Fie S o multime de clauze in ORL , si daca exista o determinare rationala a clauzei C din multimea S de clauze, atunci S implica logic pe C.

Demonstratie

Poate fi facuta printr-o inductie simpla asupra lungimii determinarii rationale. Pentru inductie trebuie sa aratam doar ca oricare pas al unei determinari date este puternic. Sa presupunem ca C₁ si C₂ sunt clauze arbitrare in ORL a caror rezolvare produce o noua clauza

(1)

unde σ este mgu al si , sunt siruri de caractere OI similare; sunt siruri de caractere similare. Pentru a demonstra ca (1) este puternica trebuie doar sa aratam ca

(2)

este OI-valid pentru orice I_R si U_R.

Pentru ca σ este mgu pt si se poate scrie si , (2) se poate scrie:

(3)

Prin deductie, avem C₁ si C₂ care sunt OI valide, de aceea, daca este OI valida, atunci este OI inconsistent, astfel este OI valid. Din nou, daca este inconsistent, atunci este OI valid. De aceea valoarea de adevar a ecuatiei (3) si anume este OI valid. Deoarece determinarea initiala a C₁ si C₂ , respectiv este OI valid.

Concluzie

Lucrarea propune folosirea sistemului ORL. Intervalul de operare care este construit prin proprietatile de aproximare inferioara si superioara bazate pe teoria multimilor difuze se poate determina prin formule matematice.

Acestea arata ca ORL este definita de alte logici cu valori multiple. Pe de alta parte, relatiile sunt folosite ca propozitii si predicate in ORL, in timp ce relatiile in sine nu pot fi definite usor; poate ca aceasta este complexitatea ORL.

MODUL PROBABILISTIC DE ACCES LA GENERAŢIA DE

ALGORITMI DE DECIZIE IN CAZUL ATRIBUTELOR

CONDIŢIONALE CONTINUE

SISTEMUL INFORMAŢIONAL SI REGULILE DE DECIZIE

Un sistem informational cu m atribute conditionale continue poate fi tratat ca o multime finita de obiecte care sunt descrise de un numar de relatii:

(X⁽¹⁾, X⁽²⁾,X⁽³⁾,..............X⁽ⁿ⁾,d ) e R^mxD (1)

Prima coordonata m a acestei relatii determina pozitia obiectului in spatiul atributelor conditionale R^m . Ultima coordonata "I" a unei multimi elementare a deciziilor D = determina clasa obiectului. Relatia in care obiectul apartine unei anumite multimi S (S R^m) înseamna ca X = (X⁽¹⁾, X⁽²⁾, ....X^(m)) apartine lui S.

In practica informatia (1) este obtinuta experimental. Din punct de vedere al practicii este important de aratat clasele necunoscute ale noilor obiecte folosind numai valorile atributelor conditionale ale obiectelor.

Teoria multimilor difuze a fost inspiratia acestei metode. Algoritmul de decizie este alcatuit din reguli ale formulei:

(X⁽¹⁾ D ( X^(m) D ^(m) (d =j) (2)

unde D D ^(m) sunt intervale din R. Daca intervalul este egal cu (- ) atunci factorul respectiv in relatia (2) poate fi omis. Multimea D D ⁽¹⁾x.... xD ^(m) este numita domeniul regulilor de decizie. Partea dreapta a regulii din formula (2) este determinata de obiectele care sunt in sistemul informational si care apartin domeniului de reguli D . Clasa care este reprezentata de cel mai mare numar de obiecte este stabilita de multimea D. In cazul unei egalitati luarea deciziei este imposibila,atunci regula va fi numita indecisa.

Cea mai apropiata metoda de întelegere a generatiei algoritmilor de decizie poate fi tratata ca o cautare pentru cele mai bune parti ale spatiului atributelor de decizie. Caracteristicile introduse in relatia (2) pot fi folosite ca criterii de selectie a celor mai bune parti.

2. CARACTERISTICILE OPTIME

Mai întâi vom arata ca analiza sistemului informational este o realizare a proceselor nedeterminate si generale. Aceasta implica o necesitate de luare in considerare a intelegerii probabilistice. In concordanta cu aceasta întelegere este necesar ca pentru orice parte fixata a spatiului atributelor conditionale F care contin situatiile S₍₁₎, S₍₂₎, S₍₃₎,.......S_(k), sa se determine u_lj ale unui obiect din

situatia s_l cu decizia j.

Urmatoarele concepte definesc partea fixa F si realizarea fixa a sistemelor informationale:

a) Situatia S_l este numita pura daca toate obiectele ei au aceeasi decizie j D. Aceasta decizie va fi numita categoria situatiilor si situatie va fi numita situatie pura a categoriei j.

b) Suma tuturor situatiilor pure va fi numita regiunea de decizie (o anumita submultime a spatiului atributelor conditionale)

c) Un obiect din afara sistemului informational poate fi clasificat daca este gasit in regiunea de decizie, intr-o situatie pura. In situatia aceasta este o problema in stabilirea categoriei obiectului.

d) Probabilitatea ca un obiect din afara sistemului informational sa fie gasit in regiunea de decizie este numit "calitatea clasificari celui mai important". Este egal cu :

= X_l(3)

S_i - pure

unde X_I = u_Ij este probabilitatea ca acel obiect sa apartina situatiei S_i

e) probabilitatea ca un obiect din afara sistemului informational sa fie clasificat corect este numita "corectitudinea clasificarii". Este egal cu:

= u_ij(4)

S_i - pure

unde j este categoria situatiilor S_i .

Ambele caracteristici (3) si (4) ne aduc la cunostinta proprietatile clasificarii partilor F pentru orice realizare fixa a sistemelor informationale. Fie Q(F) si C(F) valorile caracteristicilor din relatiile (3) si (4).

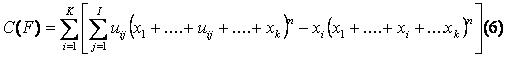
unde n este numarul de obiecte in sistemul informational x_i, trecerea peste x_l

Folosind proprietatea de aditivitate ale valorilor obtinute obtinem:

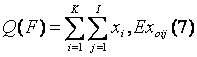
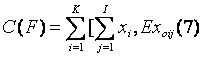
unde EX _ij este notatia valorii obtinute a x_ij

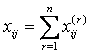
Aceasta probabilitate este egala cu . In final

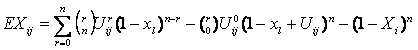
Ţinând cont de formula 7 si de proprietatile X_l = 1 obtinem formulele (5) si (6). Se folosesc de asemenea si modificarile caracteristicilor:

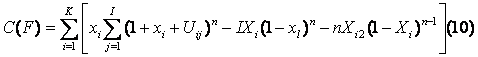
GENERAŢIA ALGORITMILOR DE DECIZIE

Orice algoritm de decizie creeaza o anumita parte D D_k= R^m a subspatiului atributelor conditionale. Oricare din caracteristicile definite in paragraful 2 pot fi folosite pentru evaluarea proprietatilor algoritmului. Toate aceste caracteristici depind de posibilitatile U_ij; obiectul care cade intr-un domeniu Dj cu decizia j si cu un numar n de obiecte in sistemul informational. Fie probabilitatea functiilor densitate f_j(x) j = 1.l cum ar fi P = _A f_j(x)dx. Avem U_ij = _Di f_j(x)dx.

Metoda propusa a generatiei algoritmilor de decizie impune estimarea probabilitatilor densitatilor claselor specifice. Autorul foloseste metoda Kernel .

Unde g este cardinalul clasei si coordonatele vectorilor X1 = , Xg = sunt valorile atributelor conditionale ale obiectelor din clasa.

Procesul generatiei algoritmului de decizie se realizeaza pe doua planuri. Primul plan consta in eliminarea valorilor intermediare ale atributelor conditionale. Fie relatia valorilor atributelor conditionale q care sunt in ordine descrescatoare ( n_q <n ) valorile intermediare sunt definite ca:

Notam:

Familia de multimi

creeaza partea spatiului atributelor conditionale R^m

Apoi pas cu pas eliminam valorile intermediare care rezulta din cea mai mare crestere a valorii calitatii caracteristicilor optime. Daca modificarea fiecarei valori intermediare rezulta din descresterea caracteristicilor optime atunci procesul eliminator se opreste.

Al doilea plan consta in folosirea situatiilor vecine care erau obtinute ca rezultat al "discretiei medii". Aceasta are loc daca se pastreaza ambele conditii:

- situatiile vecine dupa folosire au forma D x...... xD(m) unde A(1)... .A^ sunt intervale din R.

- folosirea situatiilor vecine duce la o marime a valorii caracteristicilor optime.

Procesul se opreste când folosirea sub aceste doua conditii este imposibila.

EXEMPLE ILUSTRATIVE

Metoda prezentata anterior a generatiei algoritmului de decizie a fost aplicata experimental in date privind rezistenta la frig a betonului. Sistemul contine 16 obiecte, Atributele conditionate continue reprezinta rezultatul a 5 teste care au fost realizate pentru caracterizarea proprietatilor fizice ale agregatelor înainte de folosirea lor in realizarea betonului. Clasa atributelor de decizie ia valoarea 2 in cazul unui beton rezistent la frig si valoarea 1 in celalalt caz. Rezistenta ta frig a betonului a fost stabilizata de-a lungul multor experimente.

Generatia algoritmilor de decizie este alcatuita din doua nivele, In fiecare nivel este posibil sa luam orice criteriu optim prezentat mai devreme ta bazele partii spatiului atributelor conditionale. Cele 6 combinatii ale criteriilor care au fost investigate de autori sunt aratate in tabelul 2.

Rezultatele finale ale partii spatiului atributelor conditionale in cele 6 variante. Algoritmul de decizie este obtinut din tabel prin stabilirea clasei dominante ate fiecarei submultimi de forma D x... ...xD .De exemplu algoritmul de decizie are urmatoarea forma:

X⁽²⁾ < 2.5 X⁽⁴⁾ < 1.6 X⁽⁵⁾ <4.6 => clasa = 2

X⁽²⁾ < 2.5 X⁽⁴⁾ < 1 .6 X⁽⁵⁾ 4.6 => clasa = 1

X⁽²⁾ < 2.5 X⁽⁴⁾ X⁽⁵⁾ <4.6 => clasa = 1

X⁽²⁾ < 2.5 X⁽⁴⁾ 1.6 X⁽⁵⁾  4.6 => clasa = 2

X⁽²⁾ => clasa = 1

A cincea regula este nedeterminata. Observati ca a treia regula in tabelul 3c este indecisa.

Proprietatile variantei 6 ale generatiei algoritmului de decizie au fost evaluate prin metoda" lasarea unuia afara". In concordanta cu aceasta metoda, algoritmul de decizie este generat prin folosirea tuturor obiectelor cu excluderea unuia. Apoi acest obiect este clasificat. Aceasta procedura este repetata pana când fiecare obiect a fost clasificat in acest fel.

Rata de clasificare a corectitudinii pentru cea mai buna varianta este 69% si rata erorii clasificarii omise pentru fiecare varianta nu este mai mare de 25%. Aceste valori depind de configuratia datelor la fel de bine ca si metoda de clasificare.

5. CONCLUZII

Algoritmul deciziei este unic pentru aceleasi caracteristici optime si pentru aceleasi metode de estimare a probabilitati densitatii. Algoritmul deciziei obtinut cu ajutorul clasificarii "celui mai bun" sunt închise fata de algoritmul bazat pe corectitudinea clasificarii.

Cele mai bune rezultate au fost observate prin modificarea caracteristicilor optime folosite in al doilea plan al generatiei algoritmului de decizie.

TABEL 1

ANALIZA INFORMAŢIILOR NESIGURE IN CADRU VARIABILELOR "DIFUZE"

Articolul discuta despre doua moduri de abordare a analizei datelor nestatistice:

- abordarea "multimilor difuze"

- abordarea bazata pe un model extins numit variabilele precise ale multimilor difuze

Bazele acestor doua abordari sunt prezentate si comparate in contextul unui model real descoperit in aplicatii. A fost demonstrat ca folosirea modelului variabilelor precise ale multimilor difuze, intensifica descoperirea adevaratelor capabilitati ale metodologiei multimilor difuze, particular in absenta determinantilor sau a modelelor puternic determinate in date.

1. INTRODUCERE

Acumularea datelor empirice si analiza lor este una din cele mai întâlnite teme din cercetarile stiintifice. In stiinte ca microbiologie, medicina, fizica, chimie, inginerie, formarea ipotezelor stiintifice si verificarea lor este bazata pe un numar mare de recorduri in observatii prezente sub forma rezultatelor testelor sau instrumentele citirii.

Acumularea eficienta si manipularea unor asa vaste cantitati de informatii a fost facilitata prin folosirea calculatoarelor sau a sistemelor manageriale de date. Analiza datelor si interpretarea temelor au fost realizate numai in interiorul metodelor statistice ca o analiza multivariata. S-a recunoscut ca tehnica statistica a pierdut un numar important de proprietati ale datelor, proprietati care aveau legatura cu relatiile structurale intre submultimile colectiei de date, (analiza dependentei datelor nestatistice) si prezenta sau absenta modelelor de date repetabile.

Analiza si extragerea unor informatii folositoare din bazele de date prin folosirea tehnicii mergând dincolo de metodele statistice au devenit recent un subiect al cautarilor active intr-o disciplina care se referea la descoperirea si intelegerea bazelor de date [5]. Una dintre primele metodologi nestatistice folosite pentru analiza datelor a fost Teoria multimilor difuze introdusa de Pawlak [1,3,4]. Aceasta metodologie este singura tehnica pentru analiza datelor, realizata cu o întreaga rigoare matematica in interiorul unui târâm al logicii si al sistemelor teoretice. Teoria multimilor difuze extinde teoria clasica a sistemelor prin incorporarea intr-un model de sistem al notiunilor de clasificare a informatiilor. Aceasta aparenta mica adaugare rezulta din consecintele profunde de percepere a notiunilor de sistem, relatie, functie. In acest mod de abordare, orice sistem in general este exprimat prin posibilitatea clasificarii informatiilor in aproximativ trei zone: zona pozitiva, zona de granita (limita), zona negativa.

Intuitiv, zona pozitiva a sistemelor este colectia acelor obiecte care pot fi clasificate ca apartinând acelor sisteme bazate numai pe informatii accesibile. Similar, zona negativa este o colectie de obiecte care pot fi clasificate ca apartinând complementului sistemului. Zona de granita este o colectie de obiecte pentru care informatiile sunt insuficiente pentru realizarea clasificarii ambigue. In prezenta zonei de granita, specificarea sistemului devine imprecisa, imperfecta.

Zona de granita a unui sistem poate fi perceputa ca o arie unde nu exista ambiguitati, erori libere, clasificarea obiectelor fiind posibila. O largire naturala a acestei idei este aceea de a defini zona de granita ca o arie unde clasificarea cu o eroare mai mica decât cea a nivelului prestabilit este imposibila. De aceea zonele pozitive si negative ale sistemului ar putea fi definite ca arii unde cea mai apropiata clasificare cu o rata a erorii mai mica sau egala decât cea a nivelului prestabilit este posibila.

Aceasta extensie a modelului original al multimilor difuze pentru caracterizarea unui sistem in limitele informatiilor nesigure in numeroasele nivele ale sigurantei, este ideea principala al modelului variabilelor precise ale multimilor difuze (VPRS) [7].

In realitate analiza aplicatiilor VPRS este folositoare in rezolvarea unor probleme implicând sistemele de date cu proportii mari de situatii limita.

Folosirea VPRS in legatura cu socoteala reducerii aproximative [7] care permite identificarea modelelor reale sau a regularitatilor care altfel ar fi fost pierdute daca tehnica originala a multimilor difuze ar fi fost aplicata. Un alt aspect folositor este extensia scopului analizarii modelelor reale. Prin varianta gradelor admisibile de clasificare a ratelor erorii, câteva sunt imprecise dar puternic suportate de un numar mare de cazuri reale, modelele pot fi descoperite si folosite pentru predictia de noi cazuri.

Subiectul principal al acestei lucrari este aceea de a prezenta ideile primare ale modelului VPRS si al înrudi cu modelul originar al multimilor difuze in contextul unei analize reale si a unui model de aplicatii descoperite.

Ideea esentiala a ambelor modele si seria de exemple sunt folosite pentru demonstrarea diferentelor in modelul descoperirii capabilitatilor intre cele doua moduri de abordare.

Punctul de atractie al lucrarii este abilitatea de identificare a modelelor puternic predictive in realitatea empirica. Gasind astfel de modele este cheia importanta in modelarea empirica. Toate exemplele de modele prezentate in aceasta lucrare au fost obtinute cu ajutorul unui pachet software pentru multimile difuze bazat pe analiza reala si pe regulile furnizate de "Reduct Systems".

IDEILE ESENŢIALE ALE MULŢIMI DIFUZE

Prima componenta a modelului multimilor difuze este notiunea spatiului aproximativ. Acest spatiu aproximativ contine doua elemente:

- universul cuvintelor notat cu U

- relatia echivalenta R U x U numita relatie

Relatia este un model formal al informatiilor despre obiecte
apartinând universului U. Informatia este exprimata in limitele trasaturii
obiectelor sau a relatiilor cu alte obiecte. Dând un numar si o decizie limita a
capabilitatilor trasaturilor, câteva obiecte pot deveni de nedistins cu rezultatul pe
care universul U il împarte in clase de obiecte identic disjuncte. Obiectele din
fiecare clasa se refera la un sistem elementar sau un atom, (sunt identice numai
in privinta celor observate sau a informatiilor accesibile). Echivalenta relatiei R
corespunde sistemelor elementare de impartire.

Fie X U o submultime a lui U. Problema principala a multimilor difuze este aceea de a incerca sa gasesti o caracterizare sau un model a lui X in limitele informatiilor accesibile despre obiectele apartinând universului de cuvinte U. Cu alte cuvinte scopul este acela de a gasi o descriere a multimii X in asa fel încât statutul fiecarui obiect din U cu privire la X sa poata sa fie determinat din aceasta descriere. Descrierea esentiala este predicatul definit pentru toate obiectele apartinând lui U. Predicatul specifica conditiile necesare si suficiente, exprimate in functie de accesul la informatii, pentru un obiect ce apartine multimii X sau a complementului sau. Dificultatea este aceea ca predicatul nu poate întotdeauna sa fie constituit. Aceasta se poate întâmpla daca o multime elementara are o suprapunere partiala cu multimea X. Cum toate obiectele din multimea elementara sunt identice, statutul fiecarui membru al multimii in acest caz nu poate fi determinat fara ambiguitate. Nu întotdeauna se poate forma o descriere a multimii X. Cel mai bun lucru pe care putem sa-l facem este aceea de a gasi cea mai joasa limita dar si pe cea mai ridicata limita a multimii X. Limitele numite aproximarea inferioara si superioara a lui X.

Fie E o multime elementara. Aproximarea inferioara a lui X notata cu RX este o reuniune a tuturor multimilor elementare incluse in X.

RX

Aproximarea superioara a lui X notata cu RX ca o reuniune a tuturor multimilor elementare transpuse pe X

RX =

Intuitiv aproximarea inferioara numita si interior al multimii X si notat alternativ cu INT(X) este o colectie de obiecte care pot fi clasificate fara ambiguitate ca apartinând lui X in fundamentarea informatiilor accesibile. Aproximarea superioara poate fi analizata ca o multime de obiecte care pot fi clasificate eventual ca apartinând lui X. Raportul dintre masura aproximarii inferioare si masura aproximarii superioare a multimii este numit indice de aproximare.

Multimea obiectelor ale caror statut al multimii X nu poate fi determinat este numita "arie de granita (limita)" a lui X. Aria de granita este definita prin relatia:

BND(X) = RX - RX

Colectia de obiecte care poate fi clasificata pe bazele informatiilor accesibile, care nu apartin multimii X este numita zona negativa sau exteriorul lui X. Zona negativa poate fi exprimata astfel:

EXT(X) = U - RX

Daca informatia despre obiecte este suficienta pentru clasificarea tuturor obiectelor, zona de granita dispare si multimile difuze devin echivalente cu multimile standard.

3.MODELUL VARIABILELOR PRECISE ALE MULTIMILOR DIFUZE

O extensie a modelului original al multimilor difuze, este aceea de a include câteva arii de granita in aproximarea inferioara a multimi. Aceasta extensie va avea o masura mai mica a suprapunerii cu complementul multimii X decât nivelul prestabilit 0 b < 0.5. Aceasta este motivata de dorinta de a analiza si identifica modelele reale care reprezinta tendinte statistice puternice, mai bine decât dependenta identica strict functionala sau (partial functionala) a modelului multimilor difuze. Aceasta extensie permite multimii un stil de modificare pentru date chiar si in absenta unei dependente functionale. Aceasta trasatura este folositoare când nu exista reguli precise, (datorita lipsei dependentei functionale) sau sunt insuficiente in ambele sensuri mentionate. Extensia se refera la VPRS care mosteneste toate proprietatile esentiale ale modelului originar al multimilor difuze. VPRS completeaza modelul multimilor difuze ca un instrument metodologic . In ceea ce urmeaza esentialul VPRS este prezentat.

MULŢIMI APROXIMATIVE

Fie perechea (U,R) un spatiu aproximativ descris in partea a doua si fie
0 b < 0.5 aproximatia precisa a nivelului. Fiind data o submultime arbitrara X UB, baproximarea inferioara (R B) a submultimii X sau interiorul submultimii X notat cu INT_b(X), fiind definita ca o reuniune a acelor multimi elementare a carei masura de transpunere a complementului multimii X este mai mica sau egala cu b

R_bX =

b aproximare superioara a multimi X este definita ca o reuniune a atomilor a carei masura de transpunere cu multimea X este mai mare decât b

R_bX =

b zona de granita a multimi X este definita ca o reuniune a multimilor elementare a carei masura de transpunere cu multimea X este in interiorul intervalului (b b) care este:

BND_b X =

In final zona negativa sau exteriorul multimi X este definit ca o reuniune a acelor multimi elementare care se transpun peste multimea X cu o masura mai mica sau egala cu b

EXT_bX = R_b(-X)

DEPENDENTELE ATRIBUTELOR IMPRECISE

Una dintre primele aplicati ale modelului multimilor difuze este analiza dependentei reale in sistemele de informatii [2,4,8]. Un sistem informational aduce o reprezentare a colectiei obiectelor in limitele atributelor si a valorilor lor. Atributele sunt functii ale caror domenii comune sunt date de colectia de obiecte (universul). Atributele reprezinta câteva proprietati perceptibile si masurabile ale obiectelor cum ar fi de exemplu: caracteristicile fizice (greutate, temperatura).

Multimile difuze analizeaza dependentele reale in contextul sistemelor informationale care sunt concentrate in urmatoarele probleme:

1. Fiind date doua grupuri arbitrare, sa spunem C pentru conditii si D pentru decizii ale unui sistem informational; întrebarea fiind aceea a existentei dependentei functionale intre C si D indiferent de valorile atributelor apartinând lui D care pot fi determinate de valorile atributelor apartinând lui C pentru orice obiect din sistemul informational.

2. In absenta dependentei functionale problema este gasirea cel putin a dependentei functionale partiale, o dependenta functionala a submultimi corespunzatoare multimi de obiecte date.

3. Descrierea dependentei in limita regulilor logice pentru utilizarea notiunii de atribut redus sau a valorii atributului redus.

Analiza dependentei functionale si partial functionale este realizata prin aproximarea inferioara a submultimi de obiecte corespunzând diferitelor combinatii de valori ale atributelor de decizie apartinând lui D. Doua obiecte cu aceeasi valoare a atributelor in C sunt considerate echivalente. Cum numai obiectele apartinând reuniuni aproximarii inferioare pot fi atribuite unei combinatii unice de valori,( atributele apartinând lui D), proportia acestor obiecte in intrega colectie reala furnizeaza masurarea dependentei functionale intre conditia si decizia atributelor.

Pentru a extinde capabilitatile analitice ale acestei metode de identificare a dependentei nefunctionale, ideea de model VPRS poate fi folosit in locul multimi difuze originale in derivarea masurii dependentei [7J].

Fie S = (U,A,a A) un model formal simplificat ale sistemelor informationale cu U notatia colectiei de obiecte, colectia de atribute intelese aici ca functie

a : U Va (a A) asociata fiecarui obiect e U cu o valoare unica a atributului corespunzator domeniului V_a .

Orice submultime de atribute B A induce o împartire sau o relatie echivalenta INT(B) pe multimea de obiecte U prin considerarea oricaror doua obiecte cu aceeasi valoare a atributelor apartinând lui B ca identice.

Pentru a defini masura dependentei imprecise intre multimea conditiilor atributelor C A si multimea deciziilor atributelor D A, fie C* notatia colectiei claselor echivalente ale relatiei IND(C) si similar fie D* o familie a claselor echivalente ale relatiei IND(D). Fiind dat un nivel al aproximatiei 0 b < 0.5 putem spune ca aceasta multime a deciziilor atributelor D depinde de multimea atributelor de conditie:

g ( C,D, b) = card ( POS (C, D , b )) / card ( U )

unde POS (C, D , b) este o reuniune a aproximarii inferioare ale tuturor multimilor elementare ale partitiei D* in spatiul aproximarii (U,IND(C)) si card fiind notatia multimilor cardinale.

Intuitiv dependenta imprecisa a atributelor G la nivelul precis B este proportia acestor obiecte care pot fi clasificate in clase ale partii D* cu o rata a erorii mai mica ca B pe baza informatiilor reprezentate de clasificarea C*. Dependenta imprecisa generalizeaza ideea de dependenta functionala sau partial functionala cunoscuta ca dependenta difuza când b

IMPRECIZIA ATRIBUTULUI REDUS

Conceptul de atribut redus a fost introdus de Pawlak in [2] este una din cele mai folositoare idei ale teoriei multimilor difuze. Atributul redus poate fi definit dupa cum urmeaza.

Fiind data colectia C A conditia atributelor si colectia D A decizia atributelor, si apoi submultimea RED C conditia atributelor a caror masura a dependentei cu decizia atributelor D este aceeasi cu dependenta tuturor conditiilor C cu D si este minim, este numit redusul lui C. Cerinta minima a atributului redus înseamna aici ca nici o submultime corespunzatoare atributului redus are nivelul dependentei identic cu decizia atributelor D.

Determinare atributelor reduse este partea esentiala a modelului procesului descoperit in cadrul multimilor difuze. Aceasta ajuta la identificarea factorilor fundamentali care afecteaza relatia cauza-efect. Conceptul "redus" este bazat pe notiunea de dependenta functionala sau partial functionala. Prin substituirea masurii dependentei functionale in definitia "redus" cu masura dependentei imprecise a atributelor, masura care apartine aceluiasi nivel 0 b < 0.5.

O asa reducere prin definitie nu poate pastra dependentele functionale sau partial functionale. In schimb scopul este acela de a pastra masura transpunerii multimi elementare a relatiei IND(C)multimea elementara a relatiei IND(D). Acesta duce la conceptul de imprecizie sau aproximatiei reduse [4] definita ca o submultime a conditiilor atributelor RED C pentru urmatoarele doua conditii care trebuie sa satisfaca :

g (C,D, b g (RED,D, b) (conditia de pastrare a dependentei imprecise)

g (RED,D, b > g ( B,D, b) (conditia minimala) unde B este o submultime arbitrara a lui RED, B RED

Determinarea atributului redus duce la descoperirea modelelor reale aditionale, modele care reflecta câteva caracteristici frecvente ale datelor. Furnizeaza o perspicacitate in proprietatile datelor, particular când analiza relatiilor este mostenita nedeterminat.

Pentru ilustrarea acestor situatii, putem considera o colectie a înregistrarilor bancare ale clientilor, cum ar fi anii, profesia, educatie si contine informatii despre performanta trecuta a clientilor cu privire la restituirea împrumuturilor bancare acordate. Cum informatiile continute in înregistrarile profilului clientului nu contine toti factori care afecteaza capacitatea clientului de a-si restitui împrumuturile; relatia intre caracteristicile profilului si capacitatea de restituire a împrumuturilor este in realitate nedeterminata. Parametrii profilului clientului, insuficienti pentru crearea unei descrieri a performantelor clientului, sunt indicati in performantele lui intr-un sens probabilistic. De aceea calcularea impreciziei atributelor reduse sunt folositi pentru identificarea factorilor fundamentali care afecteaza performanta clientului si construiesc un model al performantelor clientului. Acest exemplu este mai detaliat in urmatoarele sectiuni ilustrând utilitatea modelului VPRS.

4. ANALIZA DATELOR IN CADRU MODELULUI VPRS

Datorita noutatilor modelului VPRS si lipsa legaturilor software nu exista experienta practica in aplicarea VPRS - ului in problemele vieti reale. Sistemul software cum ar fi de exemplu cercetarea datelor sau datelor logice suportate de analiza datelor si regulile descoperite numai in cazul teoriei sistemelor originale ale multimilor difuze. Numai exemplele ilustrate artificial sunt folosite in aceasta lucrare pentru a demonstra capabilitatile analitice ale VPRS -ului. Exemplele prezentate in aceasta sectiune încearca sa ilustreze urmatoarele doua trasaturi:

- capacitatile de identificare puternice dar imprecise a dependentei datelor când dependenta functionala este insuficienta

- capacitatea puternica de identificare a modelelor de date imprecise când dependenta functionala este puternica si regulile precise sunt insuficiente

Pentru scopul demonstratiei, va fi folosit sistemul de informati aratat in tabelul 1. Sistemul de profile contine 20 de înregistrari bancare fiecare fiind descrise in limitele atributelor urmatoare:

CITY - localitatea unde locuieste clientul

BIRTH - ziua de nastere

OCCUP - ocupatia clientului

EMPL-TYP - tipul de angajament (permanent sau temporal)

INCOME - venitul anual al clientului

DEPEND - numarul de dependente

ASSETS - averea totala a clientului

CREDIT - evolutia înregistrarii creditelor clientilor in limitele celor trei categorii de calificare : foarte bune, bune, proaste.

Obiectul de analiza este acela de a determina daca exista modele sau dependente repetabile care pot fi folosite ca o ghidare in evaluarea ratelor creditelor ale noilor clienti ai banci

DEPENDENTA FUNCŢIONALA SCĂZUTA

Cazul dependentei functionale scazute poate avea loc când numarul sau capacitatile atributelor descriptive nu sunt suficiente, când analiza datelor in interiorul metodologiei multimilor difuze, tipic celei mai mari valori precise atributive sunt transformate in câteva ranguri calificative prin impartirea atributelor principale in subramuri, prin folosirea câtorva puncte selectate.

Aceasta procedura duce la pierderea inevitabila de informatii dar ajuta la descoperirea de noi modele de date. In câteva colectii de date, selectia rezultatelor limitei "aspre" in pierderea dependentei functionale si a pierderi capacitatii de identificare a modelelor. Pe de alta parte selectia limitei "fine" duce la reguli foarte specifice cu foarte putine aplicatii in afara sistemului informational.

Pentru ilustrarea primului punct, fiecare atribut din tabelul 1 a fost împartit in doua siruri luând aproximativ puncte de mijloc al fiecarui atribut al sirului. In tabelul 2 masura dependentei partiale este 0.45.

Fie o submultime de clienti corespunzator ratei de credite "BUN". Exactitatea aproximatiei acestei submultimi in limitele atributelor din tabelul 2 este 0.15. Aceasta înseamna ca toate modelele (regulile) determinate pot fi formate numai pentru 15% din toti acei clienti care pot fi clasificati ca apartinând categoriei de credit "BUN". Cu alte cuvinte, nu va exista nici o regula de clasificare pentru ceilalti 85% de clienti. Pentru a remedia aceasta situatie putem încerca sa evaluam potentialul pentru obtinerea regulilor de clasificare imprecisa la nivelul b=0.35 pentru aceeasi categorie de credite "BUN". Un simplu calcul poate fi folosit pentru a verifica ca aproximarea inferioara imprecisa a multimi de clienti identificat de numarul clientilor cu credit "BUN" este:

GOOD

Este o reuniune a tuturor acelor atomi a caror suprafata de transpunere cu clasa "BUN" este mai mare de 0.65. Similar, putem verifica ca aria de granita calculata la nivelul 0.35 este:

BND_0,35 =

care este singurul atom cu raportul 50/50 dea lungul categoriei BUN si a complementului sau. Cum marimea aproximarea superioara imprecise este 10, aceasta da exactitatea aproximarii clasei "BUN" calculata ca la nivelul 0.35 sa fie 0.8. interpretarea acestui rezultat este aceea ca regulile imprecise pentru clasificarea cu o rata a erorii mai mica sau egal cu 0.35 poate fi obtinut si aplicat a 80% din clienti apartinând aproximarii superioare a clasei BUN. In cazuri reale asa reguli pot fi folosite pentru evaluarea masurii probabilitatii ratei de credite ale noilor clienti.

REGULILE DETERMINĂRILOR SCĂZUTE

Regulile determinarilor scazute de obicei au loc când colectia de date este buna iar informatiile disponibile nu suporta reguli puternice. Ca un exemplu sa consideram datele clientilor din tabelul U cuantificat intre o clasa mai buna prin impartirea atributului "zi de nastere" in 3 subgrupe si atributul "venituri" in 4 subgrupe. dupa aceasta a doua modificare tabelul 3 devine bine determinat pentru atributul "credite". Daca eliminam atributele suplimentare si valoarea atributelor pentru a produce acoperirea minima a diferitelor categorii de atribute de credite in limitele valorii reduse iar rezultatele prezentate intr-o forma de tabel formeaza tabelul 4.

Fiecare rând din tabelul alaturat este o regula determinata de exemplu rândul 4 poate fi interpretat ca o declaratie:

"Daca orasul este N.Y. si ziua de nastere este 2 si evaluarile sunt 2 atunci creditul este FOARTE BUN".

Puterea acestei reguli arata in coloana STR este 1 si majoritatea dintre celelalte reguli sunt slabe, suportate doar de un singur caz. Este greu sa numim aceste modele reguli tinând cont de faptul ca ele nu reprezinta doar un fapt repetabil sau regulat despre date. Reguli ca acestea vor functiona foarte greu pe noile cazuri.

Singura cale de iesire din aceasta dificultate este aceea de a micsora necesitatea unei reguli precis determinate in favoarea unei reguli imprecis determinate, dar regulile puternice sunt calculate pe baza idei de model VPRS.

De exemplu, considerând nivelul b= 0.35 regula de determinare are puterea 1. Daca "orasul" este Regina si "veniturile" sunt 2 atunci "creditele" sunt slabe. Poate sa fie înlocuita de regula imprecisa de putere 3. Daca "veniturile" sunt 2 atunci "creditele" sunt slabe. Care sunt adevarate 2 din 3. Similar, pentru regula imprecisa cu putere 6. Daca "orasul" este York si "ziua de nastere" este 1 atunci "creditul" este slab, înlocuieste regula determinata 11 si 14 aratate in tabelul 4 si sunt corecte 5 din 6 cazuri.

Regulile de acest fel reprezinta modele relativ puternice care au loc in realitate si de asemenea care pot fi folosite pentru a prezice rezultatele noilor clienti. Daca datele folosite pentru obtinerea regulilor sunt reprezentative si modelul luat la întâmplare al întregi multimi de clienti si apoi corectitudinea frecventei regulilor, pot fi interpretate ca probabilitati ale predictiei corecte.

5. CONCLUZI

Modelul descoperit in realitate este principala terna a acestui articol. Doua moduri de abordare pentru acest model descoperit si analizat au fost discutate: modul de abordare multimilor difuze si abordarea bazata pe modelul VPRS. A fost demonstrat ca VPRS - ul este mai întâi o generalizare a modelului originar, o generalizare care ajuta la descoperirea de noi modele de date. Diferite metode analitice descopera diferite tipuri de modele de date. Modelele descoperite prin multimile difuze sunt bazate pe metoda numita logica sau modele Boolean.

Metodele statistice descopera frecventa sau modelele distributiei in timp ce alte metode de date se bazeaza pe modele numerice functionale. Luând in considerare metodele folosite se pare ca obiectivele generale ale modelului sunt acelea de a construi un tipar întreg sau partial a fenomenului complex sau a sistemului.

Descoperire formelor de date ar trebui sa aiba un efect pozitiv asupra productivitatii cercetatorilor care se ocupa cu sporirea complexului de probleme in diferitele ramuri ale stiintei si ingineriei.