Geometrie Analitica
Fondatorii. Geometria analitica a fost creata in acelasi timp, de catre Rene Descartes si Pierre Fermat.
Se stia inca din Antichitate ca fiind data o curba, intre coordonatele punctelor ei exista o anume relatie, din care apoi, pe cale geometrica, erau deduse altele.
Descartes a inventat rolurile dintre geometrie si algebra, punand in primu plan, algebra; el a aratat ca invers 22322l112w , oricarei relatii intre coordonatele x, y, f(x, y)=0, ii corespunde o curba.
Incepand cu Geometria sa, din 1637, calculul literal a luat forma moderna p care o are si astazi. La Francois Viete, calculul literal avea tot o baza geometrica; pentru el, formulele
(a+b)²=a²+2ab+b², (a-b) ²=a²-2ab+b²
sunt diferite, doarece a si b sunt masuri ale segmentelor deci egalitatile
exprima strict relatii dintre arii. Incepand cu Descartes literele nu mai reprezinta lungimi de segmente, ci
numerele irationale. Ideea era trasata de Diofant,
dar s-a impus in matematici.
Descartes pleaca in cartea sa, de la
problema lui Papus:
Fie date patru drepte in plan si se cere sa se gaseasca multimea punctelor M astfel ca intre distantele lor di la dreptele dt (i=1, 2, 3, 4), sa avem relatia d d =kd d
Descartes noteaza cu x, y coordonatele punctului M si exprima prin consideratii sintetice distantele, observand ca toate sunt lineare in x, y. Deci dimensiunea produsului este datade numarul dreptelor care intervin. In cazul a cate doua drepte in fiecare parte a egalitatii, avem o acuzatie de gradul al doilea in x, y deci luindu-l pe x arbitrar fixat, il putem construi pe y cu rigla si compasul. In cazul a cinci drepte avem acelasi rezultat, deoarece o necunoscuta fie x intra cel mult la gradul al treilea si a doua, fie y, la gradul al doilea. Fixandu-l pe x, putem sa-l construim pe y. In cazul dreptelor paralele, o necunoscuta dispare si ramane cealalta necunoscuta la gradul al treilea si rezolvarea necesita si o conica, adica este o problema solida, dupa terminologia timpului, numele de problema plana fiind atribuit acelora a caror constructie era realizabila cu rigla si compasul, adica necesitau numai drepte si cercuri. In cazul a cinci drepte paralele sau in cazul a 6, 7, 8, 9 drepte, o relatie de forma
d d d d d =kd d d d
duce la o ecuatie cel mult de gradul al cincilea. Pentru gradul al treilea sau al patrulea, fixand o coordonata o determinam oe cealalta prin intersectia a doua conice. Pentru gradul al cincilea putem sa aranjam astfel ca una din necunoscute, de exemplu y, sa intervina cel mult la gradulal patrulea si pentru cel mult cinci drepte avem o problema plana; pentru 6, 7, 8, 9 drepte avem o problema solida. Clasificarea continua mai departe.
Descartes recomandastudierea si a problemelor care nu sunt plane; ca aplicatie da o generare mecanica simpla a curbelor de ecuatie polara
r=a sec²q, r=a sec q
care generalizeaza campila lui Eudoxiu si exprima ideea findamentala ca pentru orice curba avem o relatie intre coordonate, aceeasi pentru toate punctele ei iar gradul relatiei este independent de alegerea axelor.
Descartes da o metoda generala de ducerea normalei intr-un punct la o curba si introduce ovalele.
In restul lucrarii da indicatii generale privind radacinile reale ale unei ecuatii algebrice.
Descartes n-a rezolvat nici una din problemele elemntare de geometrie analitica; el n-a dat nici macar formula distantei dintre doua puncte, nici macar ecuatia dreptei. A trasat doar liniile generale.
Lucrarea lui Descartes era greu de citit de catre contemporani.
Deosebit de interesanta este introducerea cartii sale, acel Discurs asupra metodei, in care Descartes, dand criteriile ale timpului sau.
Si lui Fermat a fost publicata postum, in 1679; dar prin scrisori, ea era cunoscuta in 1637, anul aparitiei Geometriei lei Descartes.
Si Fermat a enuntat ca orice ecuatie f(x, y)=0 reprezinta o curba. Din punctul de vedere metodic, el a mers mai departe decat Descartes. Fermat a aratat ca o ecuatie de gradul intaii reprezinta o dreapta, ca
xy=const
este ecuatia unei iperbole echilaterale, ca
x²=ay
este ecuatia unei parabole; de asemenea a dat ecuatia cercului, a elipsei.
Pentru Fermat, orice relatie algebrica este simbolul unei operatii geometrice; el a creat geometria analitica, utilizand metpde geometrice in sensul lui Apoloniu.
Si Descartes si Fermat considerau o singura axa si ambele coordonate pozitive.
Primii continuatori. Francisa van Schooten, traducand Geometria lui Descartes in limba latina, a insotit-o de numeroase comentarii in care a lamurit punctele obscure. El a dat, in 1656, formulele de translatie si de rotatie plana
x'=(ax-by+p)/(√a²+b²), y'=(bx+ay+q)/(√a²+b²)
John Wallisa dat, in 1655, ecuatia generala a conicelor
y²=2px+qx²
raportate la o axa si tangenta in varf si le-a studiat pe baza acestei ecuatii.
Wallis a introdus si coordonatele negative.
Rene Sluse a dat pentru prima oara, in 1659, reprezentarea grafica a unei functii date.
Philippe lahire a scris mai multe carti despre conice. El le-a introdus necorespunzator, dar comod pentru expunere, cu ajutorul focarelor asa cum au ramas in cartile elementare actuale. Lahire a tratat analitic si teoria polarelor. El a aratat, in 1685, ca doi diametri conjugati ai unei conice sunt conjugati in raport cu asimptotele. A introdus cercul ortoptic al unei conice, adica a aratat ca multimea punctelor din care este un cerc concentric.
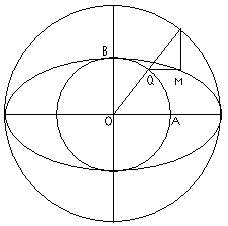 fig.
1
fig.
1
lahire a mentionat, in 1685, proprietatea comoda pentru desenarea unei elipse. A considerat doua cercuri concentrice de raze perpendiculare OA=a, OB=b (fig. 1). O secanta mobila dusa prin O taie cercurile in P si Q. Paralela din P la OB si din Q la OA se taie in punctul M, care descrie elipsa de semiaxe a, b.
O alta teorema importanta relativ la conice, data de Lahire in 1685, este urmatoarea.
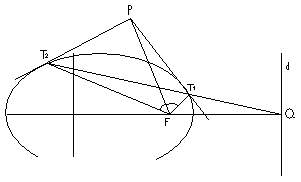 fig.
2
fig.
2
Dreapta uneste focarul unei conice cu un punct P exterior este bisectoarea unghiului format unind focarul cu punctele ale tangentelor duse din P adica (fig. 2)
<PFT = <PFT
Daca T T taie directoarea corespunzatoare focarului F in punctul Q atunci FQ este bisectoare exterioara a unghilui T FT
De asemenea, ca o aplicatie a proprietatii precedente, daca o coarda a unei conice trece prin focar, perpendiculara pe ea in focar trece prin polul coardei (fig. 3)
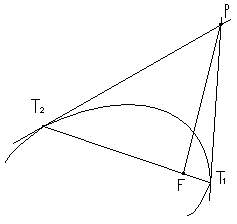 fig.
3
fig.
3
Lahire a introdus denumirea de origine si a initiat, in 1679, si geometria analitica a spatiului. El a reprezentat punctele spatiului prin trei coordonate si a dat prima oara, in acelasi an, ecuatia unei suprafete, anume a paraboloidului de rotatie
z=x²+y².
Gottfried Leibniz a introdus denumirea de abscisa, ordonata si coordonate.
Francois I'Hospital a rezolvat analitic mai multe pribleme de locuri geometrice, care duc la curbe de gradul al doilea.
Dar, in general, continuatorii nu au fost preocupatii sa refaca analitic, rezultatele cunoscute pe cale sintetica.
Ei au folosit geometria analitica, combunata cu calculul diferential si integral, pentru rezolvarea problemelor noi.
Curbele speciale. In afara curbelor cunoscute din Antichitate, secolul al 17-lea a trezit la lumina o multime de curbe speciale, studiate prin metodele combinate:sintetice, analitica si cu ajutorul analizei.
Rene Descartes insusi, ca exemplu de a obtine proprietatile unei curbe, plecand de la ecuatie, a introdus, in 1638, foliul, prin ecuatia lui
x³+y³=3axy,
retinand numai bucla din primul cadran; el a scos in evidenta simetria curbei fata de prima bisectoare, punctul dublu in origine, avand ca tangente in acest punct, axele (fig. 4).
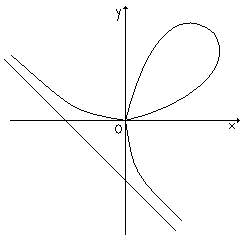 fig.
4
fig.
4
urmarind sa obtina forma cea mai rationala a lentilelor, Descartes a studiat in 1637 o clasa de ovale, determinate printr-o relatie lineara intre distantele punctelor mobile la doua puncte fixe
f|MF|+g|MG|=k
In coordonatele polare, curba are o ecuatie de forma
r²+(a+bcosq)r+c=0
Curba are doua ramuri, inverse una alteia in raport cu focarul F (fig. 5).
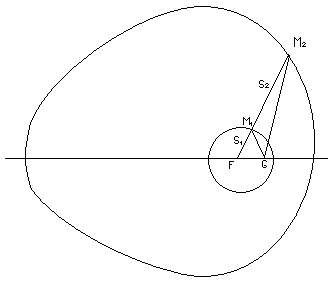 fig.
5
fig.
5
descartes a introdus in 1638 si spirala logaritmica, traiectoria unui punct mobil, supus in acelasi timp si unei ratatoo si nuei omotetii, deci este traiectoria unei asemanari (fig. 6).
Spirala logaritmica are ecuatia polara
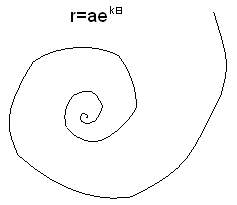 fig.
6
fig.
6
Descartes a introdus curba prin proprietatea ei de a avea arcul s proportional cu raza vectoare
s=cr
si a aratat ca spirala logaritmica isi taie razele vectoare sub un unghi constant.
De asemenea, Descartes a determinat, in 1638, normala la cicloida.
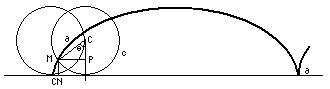 fig.
7
fig.
7
Cicloida este descrisa de un punct dat M, al unui cerc mobil c, care se rostogoleste pe o dreapta a (fig. 7).
Curba are ecuatiile
x=a(q-sinq), y=a(1-cosq
Descartes a aratat, in 1638, ca normala in punctul M trece prin punctul I de contact al cercului c cu dreapta a.
Mai general, in acelasi an, 1638, Descartes a aratat ca daca o curba c se rostogoleste pe o curba a, normalele punctelor curbei mobile c trec prin punctul de contact al celor doua curbe c si a.
Pierre Fermant a dat in acelasi an, 1638, aceeasi proprietate a normalei cicloidei.
El a calculat aria buclei foliului Descartes, aratand ca este egala cu (3/2)a².
In adevar, avem ecuatiile parametrice
x=3at/(1+t³), y=3at²/(1+t³)
si
x'=3a(1-2t³)/(1+t³)², y'=3at(2-t³)/ (1+t³)²
Atunci
![]()
Fermat a calculat aria dintre cisoida si asimptota aratand ca este de trei ori crecului generator (fig. 8).
In adevar, din ecuatia cisoidei
x(x²+y²)=ay²,
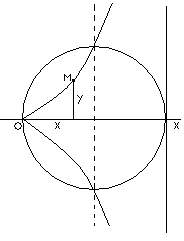 fig.
8
fig.
8
a fiind diametru cercului, avem, rezolvand in raport cu y,
y=x√x/(a-x),
luand ramura superioara. Atunci
![]()
Efectuand substitutia x=a sin²t, avem
![]()
De asemenea, Fermat a calculat aria versierei (fig. 9), curba de ecuatie
y=a³/x²+a²,
aratand ca este egala cu aria cercului de raza a.
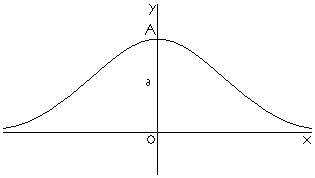 fig.
9
fig.
9
In adevar,
![]()
Gille Roberval a calculat, in 1634, aria cicloidei, aratand ca este triplul ariei cercului generator.
Evangelista Torricelli a studiat, in acelasi timp cu Descartes, spirala logaritmica, pe care a rectificat-o si a carat-o, dand frumoasele teoreme urmatoare.
Daca in punctul curent Mal spiralei logaritmice ducem tangenta MT si perpendiculara OT din O pe raza vectoare OM (fig.10), atunci
a) Segmentul MT este egal cu arcul intreg al spiralei, pornind din O.
b) Aria triunghiulara OMT este dublul ariei descrise de raza vectoare plecand din O.
Torricelli a studiat, in 1644, curba exponentiala
Y=a²
aratand ca are subtangenta constanta.
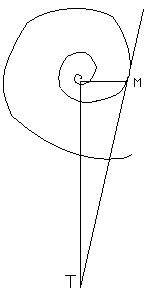 fig.
10
fig.
10
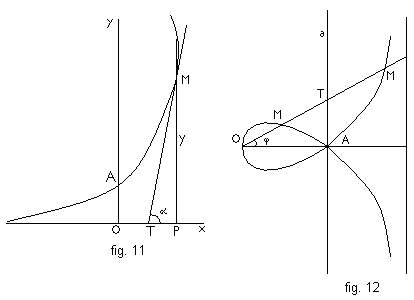
in adevar, fie M un punct al curbei exponentiale, P proiectia lui M pe axa Ox, T intersectia tangentei cu axa (fig. 11). Segmentul TP este numit subtangenta. Avem
![]()
Torricelli a introdus strofoida, descrisaastfel.
Consideram dreapta Ox si fie a o perpendiculara in A pe Ox (fig. 12). O secantamobila dusa prin punctul O taie pe a in punctul T. Putand pe secanta OT, de o parte si de alta, segmentele
TM=TM'=TA
Punctele M si M' descriu strofoida, care, daca luam originea in punctul A, are ecuatia
x(x²+y²)=a(y²-x²).
Torricelli a studiat in 1644 si cicloidele alungite sau contractate.
Francisc van Schooten a dat in 1650 regula de construire a normalelor coincide. Anume, fie curba m si n concoida a ei, adica punctele N ale curbei n sunt deduse din punctele Male curbei m purtand o lungime constanta MN=l pe razele vectoare OM care trec printr-un punct fix O(fig. 13).
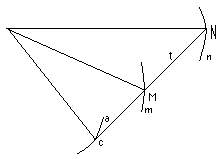 fig.
14
fig.
14
Aunci normala in punctul N la concoida trece prin intersectia I a normalei in M la curba m cu perpendiculara in O pe raza MN.
John Wallis a dat, in 1656, o formula echivalenta in fond cu
ds²=dx²+dy²
pentru calculul elementului de arc, s, al unei curbe.
Vincenzio Viviani a considerat curba de intersectie a unei sfere si a unui cilindru in pozitia particulara in care cilindrul trece prin centru sferei si ii este tangent intr-un punct A. El a calculat pe cale sintetica, in 1692, ariile determinate in cilindrul si sfera de curba de intersectie (fig. 14); a arata ca ari determinata in cilindru este 4a si aria semisferei exterioara curbei de intersectie este tot 4a. Problema a solutia data prin calculul integral, foarte simpla, a pledat hotarat in favoarea metodelor noi.
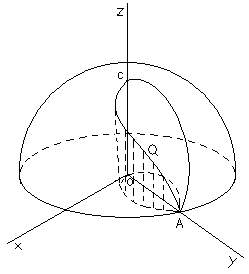 fig.
14
fig.
14
Curba de intersectie, numita fereastra lui Viviani, de fapt caz particular al ipopede lui Eudoxiu, se compune din ramura CQA si dintr-o ramura simetrica, de cealalta parte a planului zOy precum si din simetricele acestora fata de planul xOy.
Rene de Sluse a studiat in 1658, perlele de diferite forme dupa valorile constantelor. De exemplu, pentru m=1, n=3, p=2, k=-1/a² adica a²y²=x³(a-x).
Sluse a aratat ca perla este simetrica fata de axa Ox, interioara cercului de diametru OA, ca are un punct de intoarcere in origine si un maxim pentru x=3a/4.
Sluse da urmatoarea generare a acestei perle ca loc geometric.
Fie M un punct al segmentului OA si L un punct exterior segmentului, pe aceeasi dreapta pentru acer ML=a. Perpendiculara in M pe axa taie cercul de diametru OA in punctele N, N'. Paralelele din O la LN, LN' taie ordonata considerata in punctele P, P' care descriu perla.
Sluse a aratat ca perla are arie dubla cercului de raza OA/4.
Sluse a intreprins primele cercetari in legatura cu punctele de inflecxiune.
El a aratat ca prin rotirea cisoidei si a cercului fundamentale in jurul asimtotei, obtinem volume egale.
Sluse a dat o generare plana a spiricelor.
Blaise Pascal a propus mai multe probleme in legatura cu cicloida, ca determinarea volumului obtinut prin rotatia arcadei si centrul de greutate al arcadei sau a arcului de cicloida.
Domenico Cassini a introdus punctelor mobile la doua puncte fixe F, F' este constant:
MF*MF'=const.
Ecuatia ovalelor Cassini este
(x²+y²)²=a²(x²-y²)+k, a +4k>0.
Aceste ovale au diferite forme, dupa valorile lui a si k. Cand F, F' coincid regasim cercul (a=0). Cand k>0 curba este formata din doua ovale (fig. 16).
Cristiaan Huygens a introdus notiunile de evoluta si de evolventa.
Evoluta sau desfaurata unei curbe este infasuratoarea normalelor ei; ea este tot odata locul centrlor de curbura.
Invers, se presupune data curba c; evolventa ei este locul geometric p al punctelor P, situate pe tengenta in punctul mobil M al curbei c, a caror tangenta a curba p sa fie perperdiculara pe MP (fig . 17).
Daca A este originea arcelor d curbura c, atunci arcul s+MP are o lungime constanta l si curba p este generata de extremitatea unui fir de lungime constanta l, care se infasoara pe curba data, plecand din originea A panain punctul Mpe curba, iar restul firului este intins pe tangenta in M.
Avem o infinitate de evolvente, dand diferite valori lungimii l. Aceste evolve sunt curbe paralele.
Huygens a aratat in 1658, ca evoluta unei cicloide este egala cu curba tautocrona, in sensul ca oride unde ar pleca punctul M, fara viteza initiala, de pe curba si mischandu-se pe curba, el ajunge in punctul cel mai jos, A, in acelasi timp, anume a fiind raza cercului generator.
T=π√a/g.
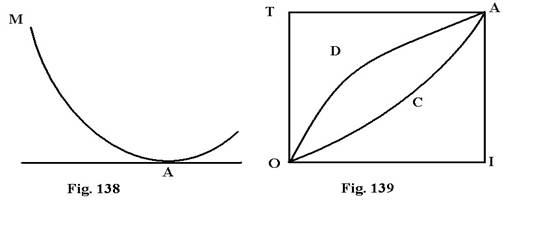
Huygens a aratat ca aria segmentului OCAD determinat de arcul de cerc si de cisoida (fig. 139) este dublul ariei OTAD.
Huygens a aratat ca aria dintre tractoare si asimptota este jumatate din aria cercului cu raza, distanta a de la vrf la axa.De asemenea a aratat ca aria si volumul obtinute prin rotatie in jurul asimptotei sunt aria sferi de raza a si jumatate din volumul aceleiasi sfere[51. b].
Huygens a studiat curba logaritmica
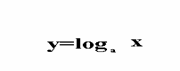
Rectificand-o si aratand in 1669, ca subtangenta pe axa Oy este constanta.
Huygens a rectificat in 1659 arcul de parabola, observand ca se exprima in logaritmi.
In adevar, pentru parabola y(la puterea a2-a)=2px luand ca parametru ordonata y ,avem pentru arcul de curba dintre varf (y=0) si un punct mobil arbitrar
Cu aceasta a observat ca acelasi rezultat a fost obtinut de Federigo Commandino ,cand a rectificat spirala lui Arhimede r = a0.
Huygens a aratat in 1673 ca o epicicloida este infasurata de cercuri mobile cu centrul pe un cerc dat cu raza variabila dupa o lege data.
Christopher Wren a aratat in 1658, ca lungimea arcadei cicloidei este de patru ori diametrul cercului generator.
Philippe Lahire a intreprins , in 1666, un studiu sistematic al epicicloidelor si ipocicloidelor ,nascute de un punct dat al unui cerc mobil care se rostogoleste exterior sau interior pe un cerc fix.El a aratat in 1706 ca daca un cerc se rostogoleste interior pe un cerc de raza dubla ,orice punct al cercului mobil descrie un diametru al cercului fix si orice alt punct, legat invariabil de cercul mobil genereaza o elipsa [50. d].
Lahire a aratat ca desfasurata unei epicicloide sau ipocicloide este o curba asemanatoare.
l fiind raportul razelor cercurilor.
Lahire a dovedit ca prin reflectie, caustica unui cerc este o epicicloida.Caustica prin reflectie a unei curbe c este infasuratoarea razelor reflectate pe curba, ale razelor care trec printr-un punct dat.
In 1706, Lahire a studiat evolventa cercului, obtinandu-i ecuatiile parametrice
X= a (cos 0 - 0 sin 0), Y= a(sin 0 + 0 cos 0).
In adevar, avem formulele pentru evolventa
X= x + rx', Y= y + ry'
unde s + r =l (constant).In cazul cercului,
X= r cos 0, y= r sin 0
avem s= -a0: luam l = 0 deci r = a0.In coordonate polare
ceea ce este evident in figura.
Conform definitiei evolventei avem
PM=arc PA, P'M' = arc AP'
deci daca este trasata curba , putem sa rectificam mecanic, cercul.
Isaac Newton a clasificat cubicele, considerand astfel parabola punctata
cu punct izolat in origine si parabola nodata
cu un nod in origine.
Newton a dat o generare mecanica a conicelor si a curbelor de grad superior. Anume, fie A, B doua puncte fixe si alfa , beta doua unghiuri de marime constanta : unui punct M, mobil pe o linie l, ii corespunde un punct N astfel ca unghiul MAN = alfa, unghiul MBN = beta, care descrie o conica.Daca M descrie o conica ,N descrie o cuartica cu trei puncte duble, doua fiind plasate in A si B.
Newton a introdus in 1671 notiunea de centru de curba intr-un punct la o curba plana si a dat expresia razei de curbura la curba x= x(t), y = y(t),
Newton a introdus notiunea de contact intre doua curbe in 1687.Anume doua curbe plane c1,c2 au un contact n - punctual in punctul M, daca au n puncte confundate in M.Daca y = f(x), y = g(x) sunt ecuatiile curbelor , pentru ca ele sa aiba un contact n-punctual in x0 trebuie ca ecuatia
F(x) - g(x) = 0
sa aiba o radacina multipla de ordinul n in x0.
Gottfriend Leibniz a clasificat curbele, in 1679, in algebrice si transcendente.
El a introdus in 1692 notiunea de curbe paralele ; sunt curbele obtinute dintr-o curba data , purtand segmente constante pe normala , plecand din punctele mobile ale curbei.
Leibniz a considerat in 1715, astroida , curba cu patru puncte de intoarcere, simetric distribuite.Curba are ecuatia a iind distanta OA de la centru la un punct de intoarcere.
Leibniz a studiat in 1693 ,tractoarea , curba care are tangentele egale , adica MT = const. = AO.
El a dat in 1692 , regula de obtinere a infasuratoarei unei familii de curbe f(x,y,delta)=0 prin eliminarea parametrului delta din aceasta ecuatie si derivata in raportul cu delta.
Walther Tschirnhaus a studiat in 1682 causticele unei curbe. Fie punctul o si curba c ; raza OM se reflecta dupa MP , adica razele OM,MP sunt egal inclinate pe normala MC in punctul M.Tschirnhaus a aratat ca punctul P in care raza reflectata a mijlocului segmentului MC, C fiind centrul de curbura in punctul corespunzator M al curbei date c.
Jacob Bernoulli a studiat in 1692 spirala logaritmica , aratand ca desfasurata ei este tot o spirala logaritmica si ca aceasta curba ramane asemenea ce ea insasi.
El a introdus in 1694 ,lemniscata, prin proprietatea ca produsul distantelor punctelor ei la doua puncte fixe F,F' este constant.
MF x MF' = const. = OF la puterea a II-adeci este un oval Cassini particular , de ecuatie Jacob Bernoulli, intr-o lucrare publicata postum , a introdus clotoida , curba pentru care curbura este proportionala cu arcul, adica o curba de ecuatie intrinseca
ps=a
Lemniscata si clotoida sunt intrebuintate in comunicatii (sosele,cai ferate).
Jacob Bernoulli a propus in 1690 sa se afle ecuatia lantisorului, figura de echilibru a unui fir fixat la capete.Problema a fost rezolvata in acelasi timp de Leibniz,Huygens,Johann Bernoulli dandu-se raspunsul
y=chx
Curba este importanta deoarece determina alura arcadei unui pod suspendat de doi stalpi.In practica ,daca picioarele podului sunt apropiate , inlocuim lantisorul printr-un arc de parabola.
Jacob Bernoulli a introdus in 1695 cercul osculator al unei curbe, limita cercului care are trei puncte comune cu curba ,cand aceste puncte se confunda.
Jacob Bernoulli a determinat in 1698, liniile geodezice ale unui con, aratand ca devin drepte in desfasurarea conului pe plan.
Pierre Varignon a introdus in 1704, spirala iperbolica, de ecuatie in coordonate polare are este inversa spiralei lui Arhimede.Spirala iperbolica admite originea ca punct asimptotic si o dreapta y=a, ca asimptota.
Varignon a introdus in 1668, transformarea
X=a0, y=r
care permite trecerea de la ecuatia unei curbe c in coordonate polare (r,0) la ecuatia altei curbe c',in coordonatele carteziene x,y si invers.In acest mod , spirala lui Arhimede r = k0 se transforma intr-o spirala logaritmica r = e la puterea "a0".
De asemenea ,tangentoida devine curba capa
r = a ctg 0
sau cuartica circulara cu punct de intoarcere in O, pentru ramura y>0, admitand dreptele y = +/- a ca asimptote .
Edmond Halley a aratat in 1686 , ca proiectia stereografica a loxodromei este o spirala logaritmica.
In adevar , proiectia stereografica fiind o reprezentare conforma si meridianele devenind drepte concurente, obtinem in proiectie o curba care taie razele vectoare sub un unghi constant , deci o spirala logaritmica .
Francois l'Hospital a dat formula razei de curbura in coordonatele polare r = r(0),
El a scos in evidenta , in 1696, punctele de intoarcere de speta intaia si a doua a curbelor plane.
Johann Bernoulli a aratat ca cicloida este o curba brahistocrona, adica, dintre toate curbele care trec prin doua puncte A si B ,timpul cel mai scurt de parcurgere al arcului AB al unui mobil greu, fara viteza initiala, este arcul de cicloida .Acesta este primul exemplu de calculul variatiilor.
El a aratat ca pentru o cicloida , caustica este o cicloida generata de un cerc cu raza jumatate din raza cercului initial.
Johann Bernoulli a introdus in 1697, notiunea de traiectorie de unghi alfa, a unei familii de curbe , anume o curba care taie toate curbele familiei sub acelasi unghi alfa.Fie f(x,y,a)= 0 ecuatia familiei de curbe.Intr-un punct M, tangenta are coeficientul unghiular y'; pentru dreapta care face unghiuyl alfa cu tangenta avem
eliminand parametrul a obtinem ecuatia traiectoriei.In particular , pentru alfa= pi/2 avem traiectoriile ortogonale.
Johann Bernoulli a aratat in 1698, ca planul osculator al unei linii geodezice pe o suprafata este perpendicular pe planul tangent.A determinat geodezicele unei suprafete de rotatie considerand o banda din cilindrul circumscris de-a lungul unui paralel si folosind proprietatea ca prin desfasurare, geodezicele devin drepte.
CARTI FUNDAMENTALE:
Rene Descartes: "La Geometrie" Paris,1637.Anexa la "Discours de la methode".
Pierre Fermat "Isagoge ad locos planos et solidos" (Introducere la problemele de locuri geometrice construibile cu cercul,dreapta sau necesitand si intersectii de conice)
Jan Witt: "Elementa curvarum linearum" Amsterdam,1659.Prima carte independenta, de geometrie analitica.
Christiaan Huygens: "Horologium oscillatorium". Manuscris din 1673, publicat in Opere complete ,Haga ,1889.
Philippe Lahire: "Sectiones conicae" Paris,1679.
Isaac Newton: " Enumeratio linearum tertii ordinis" Londra, 1704
|