Realizarea spatiilor de apoximare rough ale lui Pawlak prin metoda "Identificarii exacte"

Multimea putere P(x) a universului X si familia tuturor functionalelor caracteristice (functii cu valoarea din X) sunt in corespondenta biliniara (unu la unu) cu privire la harta care asociaza fiecarei submultimi A a luiX functionalul X_a(x) : X dafinit ca X_a(x)=

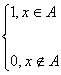
In cele ce urmeaza vom considera mai multe spatii de aproximare vaga pentru toate teoriile "rough", toate fiind caracterizari ale unei structuri abstracte definita in felul urmator: d:= unde :

1) este o latice completa in raport cu relatia de ordine partiala, legata decel mai mic element 0 si cel mai mare element 1. si , elementele din sunt interpretate drept concepte, date, etc. si se numesc elemente aproximabile.

2) D() este o sublatice a lui a acelor elemente numite definibile (descriptibile), satisfacand urmatoarele axiome 10210v2117k :

Axioma 1: Pentru orice x, exista (cel putin un element) i(x) astfel incat:

i(x)

i(x) x

i(x))

Axioma 2: Pentru orice element aproximabil x, exista (cel putin) un element O(x)astfel incat:

O(x)

x O(x)

; sau altfel zis, i(x) respextiv O(x) este cea mai buna aproximare superioara sauinferioara prin elemente definibile.

Pentru otice element aproximabil x, elementele definibile interior si exterior i(x) si O(x), a caror existenta ete asigurata de axiomele 1) si 2), sunt unice. De aceea este posibil sa introducem harta aproximarii interne, i:, si harta aproximarii exterioare O:, definit pentru : i(x):=max, O(x):=min. Aproximatia difuza a oricarui elementaproximabil x este atunci perechea ordonata r(x)=(i(x),O(x)), cu i(x)x O(x), care este imaginea elementului x prin harta de aproximatie ifuza r:, descrisa e urmatoarea diagrama:

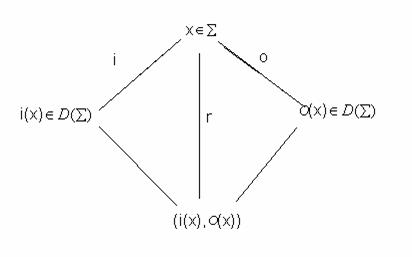
Un element x din X este numit exact daca si numai daca aproximarea lui interna coincide cu cea externa i(x O(x), sau echivalent, daca aproximarea difuza a lui este cea triviala r(x)=(x,x). Din definirea i(x), O(x) rezulta ca aceasta se intampla daca x este definibil. Deci D() este multimea tuturor elementelor exacte.

Abordarea "ortodoxa" (clasica) a lui Pawlak a teoriei multimilor difuze

Universul, formal bazat pe perechea (X, (X)) consierand dintr-o multime nevida X si o partitie (x a lui X avand ca elemente multimile elementare. Partitia (x) poate fi caracterizata e reletia e echivalenta indusa RXX, definita ca (x,y) R daca M_j (x) :x,y M_{j .} In acest caz spunem ca x si y indecelabile in raport cu R si relatia R  este numita relatie de indecelabilitate. In cazul unui univers X care este un spatiu metric compact in raport cu o functie distanta(metrica) oarecare d:XxXR definita pe el, multimea ^x a tuturor functiilor cu valori in de pe X poate fi considerata paret integranta a algebrei C^* <B (C^* ),+,0,1> a tuturor functiilor cu valori complexe marginite definite pe X, echipata cu operatiile uzuale de suma si prous, operatia de involutie-adjunctare, care tine de convergenta uniforma =sup . In particular functiile cu valori in au proprietatea de a fi proiectii ale algebrei C^* ,B(C^*) adica sunt :

adjuncte

marginite

indeplinite [(X_{aazzzaaadfgh A} X_{aazzzaaadfgh A}

In cele ce urmeaza, extinzand aceasta ternminologie la cazul general al unui univers X, functiile cu valori in efinite pe X se numesc proiectii.

Multimea ^x a tuturor functionalelor caracteristice definite pe X determina o algebra Boole completa, atomica <^x,0,1> unde0 si 1 sunt functionalele caracteristice ale multimii vide [xX,0(x)=0] si a intregului univers [xX,1(x)=1]. Operatiile sunt definite xX de proprietatile:

X_a X_b)(x)=min=max= X_a(x)X_b (x)

X_aX_b x) = max =min =

= X_a(x)+X_b (x)- X_a(x)X_b (x)

(X_a)(x)=(1- X_a)(x)=

Harta X: P(X)^x, AX_A, este in mod evident un izomorfism de latici booleene identificand P(x) si ^x, fiindca :

X X_A X_B

X= X_A X_B

X_A^c= X_A

Izomorfismul pastreaza de asemenea relatia de ordine partiala deoarece AB x, X_A(x) X_B(x).

Sa consideram acum un spatiu de aproximare "rough" determinat pe un univers X finit,de o partitie (finita) (x)=[M_i : iI} a multimii elementare ( extensiala un univers generic cu o partitie numarabila e imediata). Multimea corespondenta a functionalelor caracteristice , imprumutand terminologia analiza functionala , este o identitate precis determinata P:I^X,iP(c)= X_M, , in sensul ca satisface proprietatile:

1) toate functionalele P(i) sunt proiectii nenule ( cu valori reale, marginite si idempotente)

2) ij, P(i) P(j) P(i)P(j)=0 (conditia de ortogonalitate)

3) _iI P(i)=1

Laticea booleana corespunzatoare (x)=[M_j : JP(I)} de multimi definibile poate fi reprezentata de familia functiilor caracteristice

care genereaza o masura P cu valori-proiectie

P:P(I) ^x , J P(J)=XM_j in sensul ca satisface urmatoarele proprietati.

P1) P(I)=1

P2) J₁UJ₂=0

P3) pentru orice familie de submultimi (distincte doua cate doua) ale lui I, avem P(UJ_n)= P(J_n).

In cazul unui sistem de reprezentare a cunostintelor finit si cu set de real valori reale val(x) R, - partitia (x)=, introducand pentru simplificare notatia P=X_M(), genereaza rezolutia de identitate , precum si identitatea spectrala de rezolutie a observabilei reale f.

Deci aceasta implica satisfacerea urmatoarelor conditii suplimentare

f=_i P(_i)

Observati ca in contextul unei reprezentari exacte, a lui P(x), daca pentru simplificare notam:

P()=X _f-1(),

In analogie cu fundamentele mecanicii cuantice in abordare exacta, conditiile anterioare (P1-P3) iau forma unei masuri cu valori proiectie:

P1): P(val()=1

P2): ₁₂= P(₁) P(₂)

P3): pentru orice familie de submultimi disjuncte doua cate doua ale lui val() avem ca

P(U _n)=P(_n).

Spatii de aproximare Fuzzy-Rough

Sa ne amintim ca notiunea de functionala caracteristica pe universul X poate fi generalizata la notiunea de Fuzzy-Set definit ca o functie pe X, f:X[0,1]. Cea mai interesantastructura algebrica implicand multimi fuzzy este algebra BZMV de tip De Morgan.

<[0,1]^x,0,1,> cu operatiile definite astfel:

fg=min

fg=max

f(x)=(1-f)(x)

f(x)=

Dupa Chang, substructura algebrica <[0,1]^x,0,1> este o algebra standard MV .

Sa ne amintim ca intr-o algebra MV putem introduce de asemenea urmatoarele operatii:

(f g)(x) (fg)g](x)

(fg)(x)=[fg)g](x)

(fLg)(x)=(fg)(x)

Primele doua noi operatii sunt operatii de latice binara, generand ordinea partiala:

fg daca fg=f daca fLg =1

Trivializand, pe multimi fuzzy, relatiile de mai sus iau formele:

(f g)(x)=min si (fg)(x)=max mai mult ordinea partiala se dovedeste a fi ordonarea punctuala a functiilor de valori reale: fg daca xX, f(x)g(x). Cea de-a treia operatie binara corespunde implicatiei Lucasicnoicz conective pentru logicile cu valori multiple de adevar.

(fLg)(x)=min

In ceea ce priveste ordinea partiala, substructura

<[0,1]^x,0,1> este o latice distributiva de tip Browner-Zadeh (BZ) echipata cu doua negatii neclasice: negatia Kleene (cea care incalca principiul noncontradictiei ff0, si principiul tertului exclus ff1), si negatia Browner (care poate incalaca legea negatiei duble puternice, adica ff, si principiul tertului exclus ff1)

Oricarei multimi difuze f [0,1]^x putem sa-i asociem doua submultimi ale universului X

I(f)=, O(f)=

numite suport intern (interior) si suport extern sau (exterior).

In contextul teoriei fuzzy-set se poate construi spatiul de aproximare fuzzy-rough:

A_f <[0,1]^x,^x, H,Y> considerand in:

laticea completa distributiva de tip BZ [0,1]^x a tuturor multimilor difuze ca elemente aproximabile

laticea booleana completa ^x a tuturor multimilor clasice ca elemente definibile.

Harta aproximarii interne H: [0,1]^xx care asociaza oricarei multimi fuzzy f, necesitatea ei exacta H(f)=X_I(f), adica cea mai buna aproximare in lipsa a lui f prin elemente(multimi) exacte.

Harta aproximarii externe, asociind oricarei multimi fuzzy f probabilitatea ei Y(f)=X_O(f), cea mai buna aproximare a lui f prin adaos prin multimi exacte.

Sa ne amintim ca hartile H,Y sunt operatori modali S₅ pe laticea distributiva Kleene a tuturor multimilor fuzzy, adica ele constituie o algebrizare a modelului logicii modale, pe o structura K-S₅. K, laticea de baza nu este algebra Boole ci Kleene.

Aproximatia rough a unui fuzzy-set este deci urmatoarea pereche :

r(f)=(X,(f),X (f)), cu X_I(f)fX (f)

care poate fi identificata cu perechea de submultimi ale lui X constand in suporturile extern si intern:

r(f)(I(f),O(f)), cu I(f)O(f).

In analogie cu abordarea ne-exacta a mecanicii cuantice, putem construi spatii de aproximare Rough generalizand notiunea de rezolutie de identitate la rezolutia de fuzzy de identitate.

O rezolutie fuzzy de identitate (=partitie a universului0 este orice colectie _f(x)= de multimi fuzzy satisfacand urmatoarele conditii:

1) f_i sunt cu valori reale, nenule [f_i0] pozitive si cu absorbtie [0f_i1] astfel zis f_i[0,1]^x.

2) ij, f_i f_j (in general, asta nu implica f_i f_j=0) conditia de ortogonalitate.

3) f_i=1 (rezolutia de identitate)

Oricarei rezolutii de identitate _f(x) a lui X ii putem asocia doua familii de submultimi:

I(_f(x))=

O(_f(x))=

Numite acoperirile interioare si exterioare ale lui X induse pe _f(x).

Granula interioara si granula exterioara determinata de partitia _f(x). Pe I in punctul xX, sunt definite ca :

G_i(x)=, g₀(x)=

Granula interioara poate fi vida, dar urmatorul lant de incluziuni ramane valabil:

g_i(x) g₀(x)

Acum dorim sa aratam cum poate fi obtinuta canonic ca realizare fuzzy a unei rezolutii de identitate exacta.

Fie o variabila aleatoare f:Xval(x), asociata unui atribut dintr-un sistem de reprezentare a cunostintelor S_i. Fie identitatea spectrala a lui f, satisfacand in particular conditia spectrala f=_iP (_i).

Atunci pentru orice functie u:val()[0,1] cu multimea de valori in mod necesar finita, putem introduce:

F^(u)=P()care este o multime fuzzy F^(u) =Xf^-1 (x).

Aceasta multime fuzzy e realizata pe aceeasi partitie (x)= a atributului, setul valorilor posibile s-a scimbat insa de la R, la valorile [0,1].