Inegalitati de baza. Metrici, norme si produse scalare în 
I. Sa se arate ca au loc urmatoarele inegalitati:
(Cauchy - inegalitatea mediilor) 
.
2) (Bernoulli) 
, cu toti 
de acelasi semn ,
.
Caz
particular: 
.
3) (Hölder) 
,
.
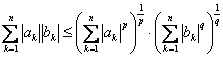Caz
particular: 
(Cauchy - Buniakowski - Schwarz)
.
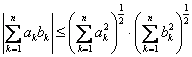4) (Minkowski) 
,
.
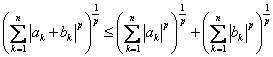II
II.1) Sa se verifice ca urmatoarele aplicatii definesc distante (metrici) pe multimile în cauza:
a) 
b)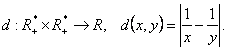 
c)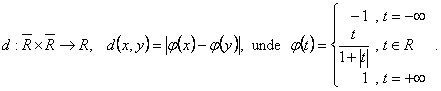 
d)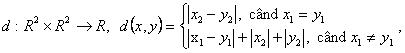 
e) 
f) 
.
g)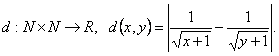 
h) 
i)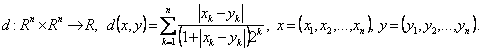 
II.2) Fie 
o metrica. Sa se arate ca urmatoarele aplicatii sunt
de asemenea metrici pe 
: 
; 
, cu 
(constanta); 
; 
; 
. Sunt acestea echivalente cu d ?
II.3) Se considera , astfel încât:
i) 
si
ii) 
.
Sa
se demonstreze ca d este o
metrica pe (Lindenbaum).
II.4) Daca d este o
metrica pe , sa se arate ca au loc relatiile:
a) 
(inegalitatea
triunghiului);
b) 
(inegalitatea
patrulaterului).
II.5) a) Fie
si 
doua metrici pe . Sa se arate ca 
si 
sunt, de asemenea,
metrici pe .
b) Fie 
, metrici pe 
. Sa se demonstreze ca urmatoarele
aplicatii 
, definite respectiv prin
,
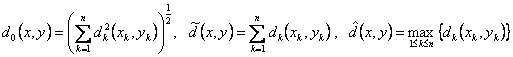, sunt metrici pe 
.
c)
Sa se arate ca daca
si 
sunt doua
metrici, atunci 
, definita prin
,
este o metrica.
II.6) Fie d o metrica pe si 
vectorul nul din . Se considera 
,
definita prin:
.
Sa se arate ca:
a)
este o metrica pe
, iar topologia indusa de d este mai putin fina decât cea indusa de ;
b)
,
unde indicele "0"
desemneaza entitatile în cauza ( diametrul multimii
si respectiv sfera ) definite prin intermediul metricii .
III.1) a) Folosind inegalitatea lui Minkowski , sa
se arate ca aplicatia 
,
definita prin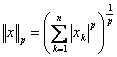 
, 
, unde 
este indicat,
constituie o norma pe .
b)
Sa se arate ca 
.
c)
Sa se verifice ca
normele 
(norma
euclidiana) si 
sunt echivalente,
demonstrând ca:
.
d) Sa se arate ca 
.
e) Sa se observe ca
inegalitatea lui Hölder se poate reda sub forma 
, unde 
înseamna produsul
scalar euclidian al elementelor x
si y, adica 
, 
, 
. În particular, când 
, inegalitatea lui Cauchy - Buniakowski - Schwarz se poate
scrie în forma:
.
III.2)
Fie 
o norma pe . Sa se arate ca:
a) 
.
b) 
.
c) 
.
III.3)
Fie 
si 
definite prin 
, respectiv
, 
, unde 
sunt constante. Date
fiind
si 
, astfel încât 
, se considera aplicatiile 
si
, definite respectiv prin:
.
a)
Sa se arate ca 
si 
sunt norme pe 
.
b)
Sa se demonstreze ca
daca exista 
, astfel încât 
si 
, atunci 
este de asemenea o
norma pe . Conditia 
este si
necesara sau
doar suficienta pentru ca sa fie o
norma pe ?
III.4)
Fie 
o norma pe si 
, definita prin:
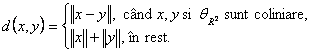
Sa se arate ca:
a)
d este o metrica pe 
, iar topologia indusa de d este mai fina decât cea indusa de norma .
b)
, unde 
si S semnifica diametrul si
respectiv sfera în raport cu d, iar 
este notatia
pentru norma euclidiana pe .
IV
IV.1) Sa se arate ca urmatoarele
aplicatii 
, definite dupa cum urmeaza, sunt produse scalare
pe 
:
a) 
,
b) 
.
IV.2) Fie 
un produs scalar pe si norma indusa.
a) Sa se arate ca au loc relatiile:
(i) 
(ii) 
b) Când 
, sa se arate ca are loc egalitatea 
, precum si
relatia : 
.
c) Reciproc, sa se arate ca daca
, în , are loc egalitatea sau relatia
, atunci x si y sunt vectori ortogonali, adica .
IV.3) Fie 
, 
, 
si 
, unde este un produs scalar
pe . Sa se arate ca:
a) 
, unde este norma
indusa de pe .
b) pe baza relatiei de la a) si a egalitatii
,
unde 
si d este metrica indusa de norma , distanta de la 
la A are
valoarea 
si 
, ori de câte ori 
.
IV.4) Fie W
un subspatiu liniar al lui si 
o functie
liniara, neidentic nula, pentru care 
. Se defineste aplicatia 
, prin 
. Sa se arate ca:
a) 
este un spatiu
prehilbertian.
b) Oricare doua elemente ale lui W, diferite de 
, sunt liniar dependente.
F. Iacob / 27.09.2005
|
