ALTE DOCUMENTE
|
||||||||||
FUNCŢII DERIVABILE
a). Definitie: Fie
![]() si
si![]() , x0 punct de acumulare.
, x0 punct de acumulare.
b). spunem ca functia 919e46j f are derivata īn punctul x0 daca exista limita īn R:
![]() notata cu f (x0).
notata cu f (x0).
b). Daca derivata f (x0) exista si este finita se spune ca functia 919e46j f este derivabila īn x0.
Observatii:
![]()
1). Facānd translatia ![]() , rezulta:
, rezulta:
2). Utilizānd notatiile:
![]()
rezulta:
![]()
Defini![]()
tie: daca functia 919e46j ![]()
![]()
este
derivabila īn orice punct al multimii![]() , atunci se spune ca f este derivabila pe A.
, atunci se spune ca f este derivabila pe A.
Functia
![]() se numeste derivata lui f pe multimea A si se
noteaza f'.
se numeste derivata lui f pe multimea A si se
noteaza f'.
Din observatia 1), daca f este derivabila pe D avem:
![]()
Teorema:Orice functie derivabila īntr-un punct este continua īn acel punct.
b) Derivate laterale.
Derivata
la stānga īn punctul 
Derivatele functiilor elementare:
![]()
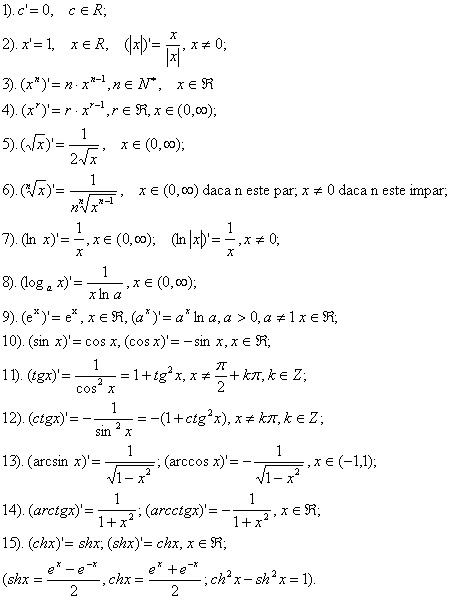
Tabloul de derivare al functiilor compuse:

d). Interpretarea geometrica a derivatei:
![]() este
coeficientul unghiular al tangentei la graficul functiei
este
coeficientul unghiular al tangentei la graficul functiei ![]() in punctul
in punctul ![]() .
.
Ecuatia tangentei in acest punct fiind: ![]() .
.
Este posibil ca derivatele laterale sa existe dar sa nu fie egale. Putem intalni cazurile:
1). a).![]() si
si ![]() ; atunci forma graficului in jurul punctului
; atunci forma graficului in jurul punctului ![]() este:
este:
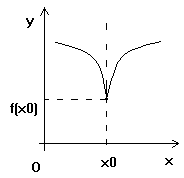
b). ![]() si
si ![]() ; atunci forma graficului in jurul punctului
; atunci forma graficului in jurul punctului ![]() este:
este:
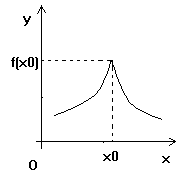
Definitie: Punctul ![]() se numeste punct de
intoarcere pentru graficul functiei
se numeste punct de
intoarcere pentru graficul functiei ![]() daca derivatele
laterale in
daca derivatele
laterale in ![]() sunt infinite si
diferite.
sunt infinite si
diferite.
2). Daca ![]() , atunci tangenta in
, atunci tangenta in ![]() este paralela cu axa
Oy.
este paralela cu axa
Oy.
3). a). ![]() , atunci forma graficului in jurul punctului
, atunci forma graficului in jurul punctului ![]() este:
este:
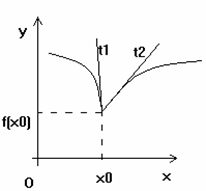

In punctul ![]() graficul are doua semitangente distincte de ecuatii:
graficul are doua semitangente distincte de ecuatii: ![]() ,
, ![]() .
.
b). ![]() . Atunci forma graficului in jurul punctului
. Atunci forma graficului in jurul punctului ![]() este:
este:
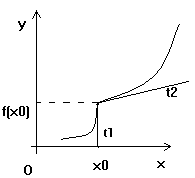

In punctul ![]() graficul are doua semitangente diferite de ecuatii:
graficul are doua semitangente diferite de ecuatii: ![]() ,
, ![]() .
.
c). ![]() . In jurul punctului
. In jurul punctului ![]() forma graficului este:
forma graficului este:
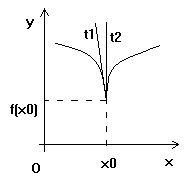
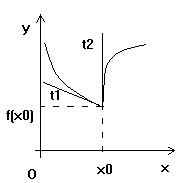
Dreptele de ecuatii: ![]() sunt cele doua
semitangente la grafic in punctul
sunt cele doua
semitangente la grafic in punctul ![]() .
.
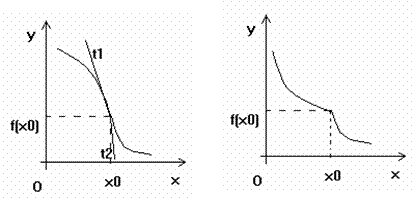
d). ![]() . In jurul punctului
. In jurul punctului ![]() forma graficului este:
forma graficului este:
Dreptele de ecuatii ![]() sunt cele doua semitangente
la grafic in punctul
sunt cele doua semitangente
la grafic in punctul ![]() .
.
e). ![]() . In jurul punctului
. In jurul punctului ![]() forma graficului este:
forma graficului este:
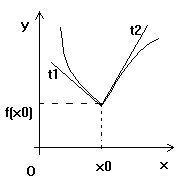
In acest caz graficul are in punctul ![]() doua semitangente
diferite de ecuatii:
doua semitangente
diferite de ecuatii:
![]()
Definitie: Daca f este continua in x0, ![]() si cel putin una din derivatele laterale este finita, atunci
(x0,f(x0))
se numeste punct unghiular.
si cel putin una din derivatele laterale este finita, atunci
(x0,f(x0))
se numeste punct unghiular.
e). Derivate de ordin superior
Fie ![]() interval sau reuniune
de intervale din
interval sau reuniune
de intervale din ![]() si fie
si fie ![]() o functie.
o functie.
Definitie: functia ![]() se numeste derivabila
de ordinul 1 daca este derivabila. Functia
se numeste derivabila
de ordinul 1 daca este derivabila. Functia ![]() se numeste derivata de
ordinul 1 a lui
se numeste derivata de
ordinul 1 a lui ![]() .
.
Definitie: Functia ![]() este de doua ori derivabila in
este de doua ori derivabila in ![]() daca
daca ![]() este derivabila intr-o vecinatate a lui
este derivabila intr-o vecinatate a lui ![]() si
si ![]() este derivabila in
este derivabila in ![]() . In acest caz derivata lui
. In acest caz derivata lui ![]() in
in ![]() se numeste derivata a
doua (sau de ordinul 2) a lui
se numeste derivata a
doua (sau de ordinul 2) a lui ![]() in punctul
in punctul ![]() si se noteaza
si se noteaza ![]() .
.
Asadar ![]() .
.
Definitie: Functia ![]() este de doua ori
derivabila pe
este de doua ori
derivabila pe ![]() daca
daca ![]() este derivabila pe
este derivabila pe ![]() . Functia
. Functia ![]() se numeste derivata de
ordinul 2 a lui
se numeste derivata de
ordinul 2 a lui ![]() (se mai noteaza
(se mai noteaza ![]() ).
).
Definitie: Fie ![]() . Functia
. Functia ![]() se numeste derivabila de ordinul
se numeste derivabila de ordinul ![]() daca este derivabila
de ordinul
daca este derivabila
de ordinul ![]() , si daca derivata sa de ordinul
, si daca derivata sa de ordinul ![]() ,
, ![]() este derivabila.
este derivabila.
In acest caz, ![]() se noteaza
se noteaza ![]() si se numeste derivata
de ordin
si se numeste derivata
de ordin ![]() a lui
a lui ![]() .
.
Definitie: Functia ![]() se numeste derivabila
de ordinul
se numeste derivabila
de ordinul ![]() , sau functie infinit derivabila daca este derivabila de
orice ordin
, sau functie infinit derivabila daca este derivabila de
orice ordin ![]() .
.
Exercitii rezolvate:
1). Studiati derivabilitatea functiei 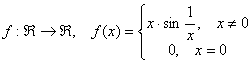 in punctul
in punctul ![]() .
.
 nu exista. Deci
nu exista. Deci ![]() nu este derivabila in
0.
nu este derivabila in
0.
2). Studiati derivabilitatea functiei ![]() , in punctul
, in punctul ![]() .
.
 .
.
Am calculat numai derivata la dreapta deoarece
domeniul functiei este ![]() .
.
Functia are derivata ![]() , deci nu este derivabila in
, deci nu este derivabila in ![]() .
.
3). Daca ![]() are derivata in
punctul
are derivata in
punctul ![]() , atunci sa se calculeze limita:
, atunci sa se calculeze limita: ![]() .
.

4). Studiati derivatele laterale ale urmatoarelor functii in punctele indicate:
a). ![]()
![]() Functia modul nu este
derivabila in
Functia modul nu este
derivabila in ![]() .
.
b). 
![]() ;
; ![]() .
.
Functia are derivata in punctul ![]() , dar nu este derivabila.
, dar nu este derivabila.
5). Aflati punctele unghiulare sau punctele de intoarcere ale urmatoarelor functii:
a). ![]() .
.
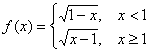 .
.
Functia este derivabila pe ![]() . Studiem derivabilitatea in
. Studiem derivabilitatea in ![]() :
:
![]() ;
;
![]() .
.
Punctul ![]() este punct de
intoarcere.
este punct de
intoarcere.
b). ![]() .
.
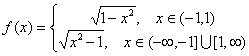
Pe ![]() functia este
derivabila. Studiem derivabilitatea in
functia este
derivabila. Studiem derivabilitatea in ![]() :
:
![]() .
.
![]() .
.
Punctul ![]() este punct de
intoarcere.
este punct de
intoarcere.
Studiem derivabilitatea in ![]() :
:
![]() .
.
![]() .
.
Punctul ![]() este punct de
intoarcere.
este punct de
intoarcere.
c). 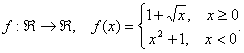
![]() .
.
Ecuatiile semitangentelor in punctul unghiular ![]() sunt:
sunt:
![]()
6). Aflati parametrii a, b reali astfel incat urmatoarele functii sa fie derivabile in punctele indicate:
a). 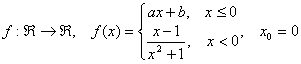 .
.
Este necesar ca functia sa fie continua in ![]()
![]() .
.
Obtinem ![]() .
.
Functia este derivabila in ![]() .
.
 Obtinem
Obtinem ![]() .
.
b).  .
.
Functia ![]() este continua in
este continua in ![]()
![]() Obtinem
Obtinem ![]() .
.
Functia este derivabila in ![]()
![]()
 Obtinem
Obtinem ![]()
7). Fie functia ![]() .
.
a). Determinati ecuatia tangentei la graficul functiei in punctul deintersectie cu axa Oy;
b). Demonstrati ca ![]() este bijectiva, cu
inversa derivabila in punctul 1 si sa se calculeze derivata inversei in punctul
1.
este bijectiva, cu
inversa derivabila in punctul 1 si sa se calculeze derivata inversei in punctul
1.
a). ![]() .
.
Ecuatia tangentei este: ![]() .
.
![]() .
.
Ecuatia tangentei: ![]() .
.
b). Functia ![]() este continua pe
este continua pe ![]() , rezulta ca are proprietatea lui Darboux
, rezulta ca are proprietatea lui Darboux ![]() interval
interval![]() .
.
![]() surjectiva.
surjectiva.
![]() .
.
|
x |
|
|
g'(x) | |
|
|
|
Rezulta ca functia g este strict crescatoare, ceea ce implica g injectiva.
Functia g fiind injectiva si surjectiva este bijectiva si deci inversabila.
![]() . Observam ca
. Observam ca ![]() este solutie; deoarece
functia este bijectiva, aceasta este unica.
este solutie; deoarece
functia este bijectiva, aceasta este unica.
![]() , rezulta conform teoremei de derivare a inversei ca
, rezulta conform teoremei de derivare a inversei ca ![]() este derivabila in 1
si
este derivabila in 1
si ![]() .
.
8). Fie functia ![]() ,
, 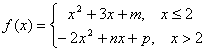 .
.
Sa se determine m, n, p numere reale astfel incat f sa fie de doua ori derivabila in x=2.
Solutie. Daca f este de doua ori derivabila in x=2, atunci functia este continua in x=2, este derivabila in x=2, este de doua ori derivabila in x=2.
f continua in x=2 
f derivabila in x=2 ![]()
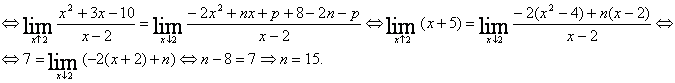 f derivabila de doua ori in x=2
f derivabila de doua ori in x=2 ![]() .
.
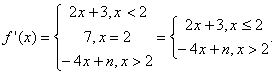
![]() imposibil.
imposibil.
Rezulta ca nu exista m, n, p ![]() pentru care functia sa
fie de doua ori derivabila in x=2.
pentru care functia sa
fie de doua ori derivabila in x=2.
9). Sa se determine m, n, p, q![]() astfel incat functia
astfel incat functia 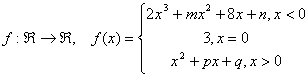
sa fie derivabila de doua ori in x=0.
Solutie: functia trebuie sa fie continua in x=0, derivabila, derivata continua in x=0, sa fie derivabila de doua ori in x=0.
Functia continua in x=0 ![]()
![]() Functia derivabila in x=0
Functia derivabila in x=0![]()
![]()
Functia  este continua in x=0.
este continua in x=0.
Functia de doua ori derivabila in x=0 ![]() .
.
![]()
10). Sa se calculeze ![]() .
.
Folosim formula lui Leibniz:
![]() .
.
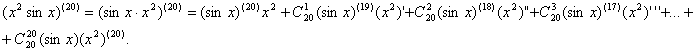 Observam ca:
Observam ca: ![]() ;
;
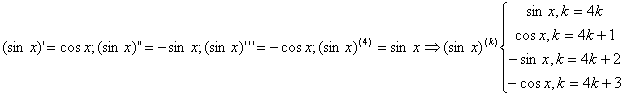
![]()
11). Sa se arate ca functiile sunt indefinit derivabile:
a). ![]() ;
;
b). ![]()
a). ![]() .
.
Intuim analizand rezultatele primelor derivate ca derivata de ordin n are forma:
![]() .
.
Acest rezultat se demonstreaza folosind metoda inductiei matematice.
I.
Verificarea:
pentru n=1, ![]() , este adevarata.
, este adevarata.
II. Etapa demonstrativa: presupunem rezultatul adevarat pentru n si-l demonstram pentru n+1:
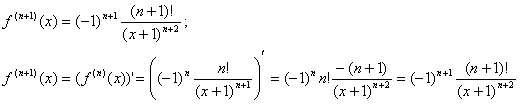
b). Calculand primele derivate ale functiei nu putem intui rezultatul pentru derivata de ordin n.
![]()
Scriem functia ca suma de fractii simple:
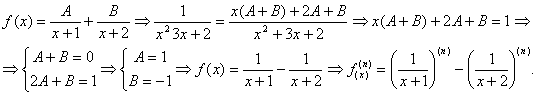
Procedand ca la punctul a), obtinem:
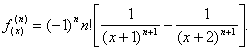
12). Calculati sumele:
a). ![]()
b). ![]() .
.
c). ![]()
a). Stim ca: ![]() (sunt termenii unei
progresii geometrice).
(sunt termenii unei
progresii geometrice).
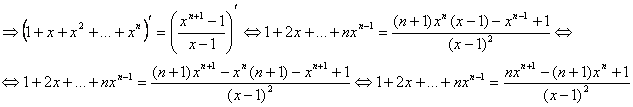 b).
b). 
c). 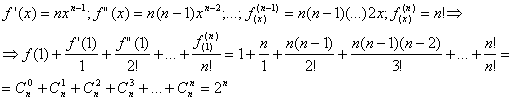
Sa se studieze derivabilitatea, existenta punctelor unghiulare si a punctelor de intoarcere a urmatoarelor functii:
a) ![]() ;
;
b) ![]() ;
;
c) 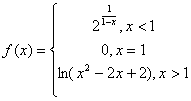 ;
;
d) ![]() ;
;
e) ![]()
2). Sa se determine numerele reale a, b, c astfel incat functia
a)  sa fie derivabila in
x=e;
sa fie derivabila in
x=e;
b) ![]() sa fie de doua ori
derivabila in x=0;
sa fie de doua ori
derivabila in x=0;
c)  sa fie derivabila in
x=0
sa fie derivabila in
x=0
Fie functia: ![]() . Sa se determine punctul M(a,b) ce apartine graficului, in
care tangenta la grafic este paralela cu dreapta de ecuatie y=2x+3.
. Sa se determine punctul M(a,b) ce apartine graficului, in
care tangenta la grafic este paralela cu dreapta de ecuatie y=2x+3.
Fie functia: ![]() . Sa se calculeze
. Sa se calculeze ![]() .
.
Fie  . Sa se studieze derivabilitea lui f si sa se determine
punctele unde tangenta la grafic trece prin origine.
. Sa se studieze derivabilitea lui f si sa se determine
punctele unde tangenta la grafic trece prin origine.
Fiind date functiile ![]() si
si ![]() , sa se determine a, b, c astfel incat graficele celor doua
functii sa aiba tangenta comuna in punctul de abscisa 1. (Indicatie: punctul de
abscisa 1: A(1,0) este punct de intersectie a celor doua grafice
, sa se determine a, b, c astfel incat graficele celor doua
functii sa aiba tangenta comuna in punctul de abscisa 1. (Indicatie: punctul de
abscisa 1: A(1,0) este punct de intersectie a celor doua grafice ![]() , au aceeasi tangenta
, au aceeasi tangenta ![]() . Se rezolva sistemul si se obtine:
. Se rezolva sistemul si se obtine: ![]() ).
).
Folosind derivatele sa se demonstreze egalitatile:
a) ![]() ;
;
b) ![]() ;
;
c) ![]() .
.
Sa se calculeze derivatele de ordin n ale urmatoarelor functii:
a) ![]() ;
;
b) ![]() ;
;
c) ![]() ;
;
d) ![]() ;
;
e) ![]() ;
;
f)
![]() ;
;
g) ![]() .
.
|