Serii de puteri

Sa se determine intervalul de convergenta pentru urmatoarele serii de puteri reale:

a)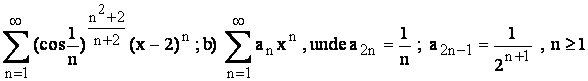

c)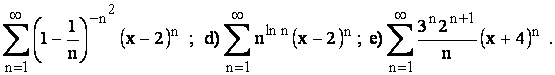 

Rez: a) .

b) =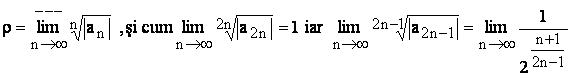

=

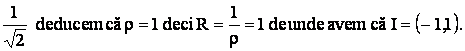
c) ,si

I=.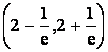

d) 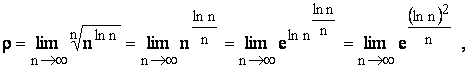însa avem ca

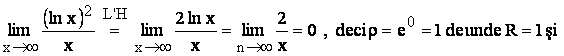
I=(1,3).

e)

.

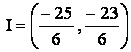Sa se determine discul de convergenta pentru urmatoarele serii de puteri complexe:

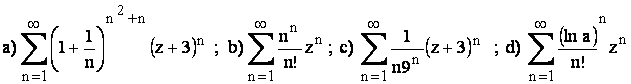
cu a>0 e) .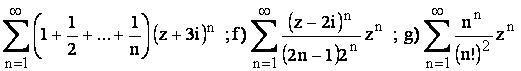

Rez:

a)

si D=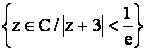

b)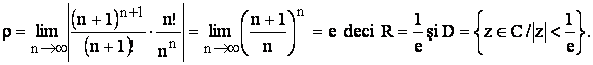

c)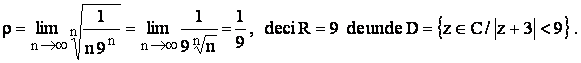

d)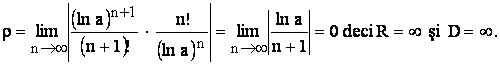

e)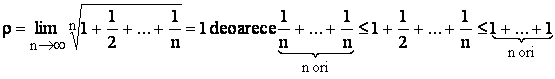

deci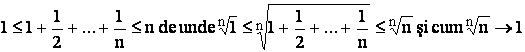

gasim conform criteriului clestelui limita 1.Deci R=1 si obtinem discul :

f)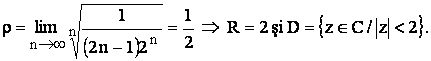

g) C .

Sa se determine multimea de convergenta pentru urmatoarele serii de puteri reale:

a)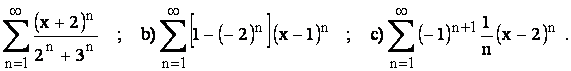

Rez: a)

Daca

Daca

Daca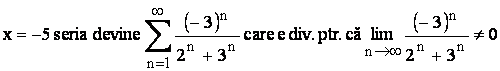

Daca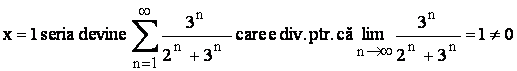

Multimea de convergenta este deci intervalul (-5,1).

b)

seama ca , deci R= .

Se impune în continuare o discutie ca si în cazul anterior, lucruri mai importante

fiind de spus în capetele intervalului de convergenta , acolo unde avem caz de

dubiu asupra naturii seriei.

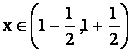Daca seria e conv.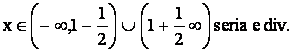

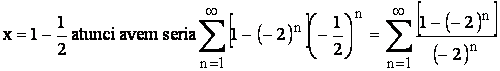Daca

Daca care e

divergenta deoarece termenul general al sau nu are limita 0 .

Daca 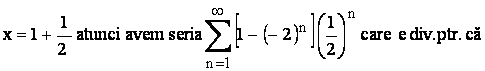sirul

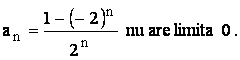Multimea de conv. este deci () .

c)

Daca

Daca

Daca

Daca 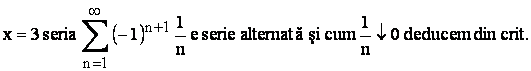lui

Leibniz ca seria este convergenta. Deci mult de conv. este

Sa se determine multimea de convergenta a seriilor de puteri complexe urmatoare :

a)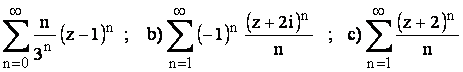

Rez:

a)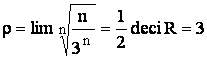

Daca

Daca

Daca

caz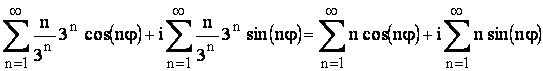

si daca presupunem ca este convergenta ar trebui ca cele doua serii de numere

reale ce o compun sa fie convergente de aceea sirurile

sa aiba limita 0 .Le ridicam la patrat si le adunam obtinând ca sirul n² are limita 0 ,fals deci presupunerea este gresita seria noastra e divergenta.

Multimea de conv este deci

b) Se obtine imediat ca raza de convergenta este R=1.

Daca

Daca

Daca

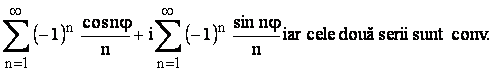pe baza criteriului lui Dirichlet, (seriile sumelor partiale marginite iar sirul ). Deducem ca seria de puteri com-

plexe este convergenta si avem.

c) Ca în exemplul anterior se obtine ca R=1.

Daca .

Daca

Daca ,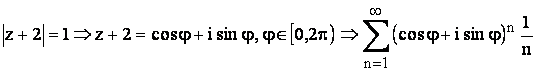

deci se obtine seria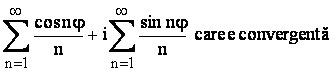datorita aceluiasi criteriu al lui Dirichlet aplicat seriilor componente .

Se deduce de aici ca seria de puteri data este convergenta pe multimea :

Sa se determine multimea de convergenta si suma seriilor de puteri urmatoare pe intervalul deschis de convergenta :

a)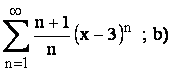

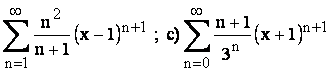
Rez:

a)     R=1 evident deci avem situatiile :

Suma se calculeaza pe intervalul (2,4) si se pleca de la seria 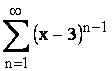care are

suma 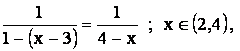se integreaza obtinându-se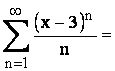

înmulteste

cu (x-3) obtinând 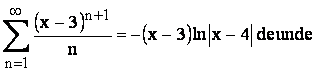prin derivare se obtine

suma seriei cautate ca fiind derivata functiei - ( x-3 )

b) .I= (0,2) interval de convergenta.

Daca x = 0 sau x = 2 se verifica imediat ca seria e divergenta deoarece termenul general nu are limita 0.

Se pleca de la seria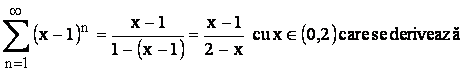

obtinând 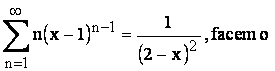înmultire cu obtinem

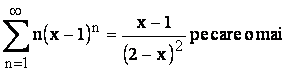derivam o data obtinând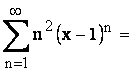

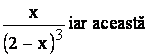=serie se integreaza : .

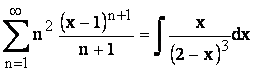constanta care se obtine din integrare se determina alegând în ultima relatie x=1.

c) .

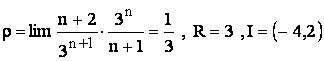Daca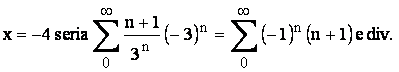

Daca 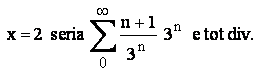Multimea de conv este deci I.

Se pleaca de la seria 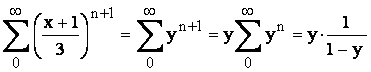unde :

Se deriveaza aceasta serie si se obtine:

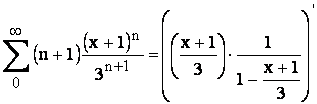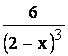= iar acum se face o înmulti-

re cu deducându-se ca suma seriei cautate este .