Statistica este asociata cu un anumit tip de prelucrare a informatiilor din lumea înconjuratoare si anume acel tip de prelucrare care clasifica, centralizeaza informatiile în tabele, si grafice, grupeaza informatiile, descopera legaturi între ele, descopera eventuale cauzalitati, analizeaza fenomene complexe. În plus, statistica face si generalizari ale unor ipoteze descoperite de obicei empiric. Chiar daca nu avem o idee precisa, cu totii gândim despre aceasta stiinta ca nu opereaza cu informatii referitoare la un pacient sau o planta sau un obiect sau la un numar foarte restrâns de astfel de entitati. stim ca statistica este stiinta care prelucreaza informatii care se refera la un numar mare de entitati cum ar fi pacienti sau indivizi sanatosi sau sau plante sau obiecte de alta natura.
Fenomenele macroeconomice, care cer manipularea si interpretarea unei cantitati uriase de date sunt deseori explicate prin estimari de natura statistica. Aprecierea evolutiei unui fenomen macroeconomic sau social în timp si estimarea modului lui de evolutie în viitor se face cu ajutorul statisticii. De exemplu, estimarea tendintei economiei unei tari pe anul urmator sau pe o perioada mai lunga se face prin metode statistice tinând cont de datele anterioare. Estimarea consumului anumitor tipuri de alimente, estimarea modului de evolutie a popularitatii diferitelor personalitati, partide, se realizeaza de asemeni prin sondaje statistice complexe, elaborate.
Utilitatea statisticii este pusa mai bine în evidenta atunci când trebuie studiate fenomene complexe în care intervin factori sau marimi care se afla în relatii complexe ce nu pot fi descrise satisfacator prin ecuatii sau formule, sau prin relatii cantitative de dependenta. De exemplu, în tehnica, daca suntem la un moment dat interesati de consumul de carburant al unui motor, exista în mod sigur o determinare destul de exacta a acestuia în functie de puterea motorului, tipul sau, viteza de deplasare, si alti câtiva parametri. Cunoscând parametrii de care depinde consumul, aplicam o formula si obtinem consumul de carburant al acelui motor. Ceea ce obtinem este valabil pentru orice motor de acelasi tip si care functioneaza în aceleasi conditii.
Daca însa am dori, în mod utopic, sa calculam numarul de leucocite pe care ar trebui sa la aiba pacientii care sufera de o anumita afectiune având datele generale despre acea afectiune si folosind cunostintele de fiziologie, biochimie, biofizica, etc, nu vom avea nici un succes. Variabilele care ar trebui sa intre în calcul sunt atât de multe si atât de complex depind unele de altele încât orice încercare de cuprindere în formule matematice este sortita esecului. În asemenea cazuri, numai abordarea statistica este posibila. Se poate doar, eventual afirma, ca exista o tendinta (semnificativa din puncte de vedere statistic), ca numarul de leucocite sa depinda într-o anumita masura de unul sau mai multi factori, si se pot chiar cuantifica aceste legaturi de dependenta. De aceste probleme se ocupa unul din capitolele importante ale statisticii, capitol tratat si în aceasta carte, anume teoria corelatiei (vezi capitolul 9).
De fapt, biologia si medicina lucreaza cu concepte, fapte, notiuni, dintre care doar o mica parte se preteaza la o interpretare determinista, exacta. Chiar daca avem impresia ca majoritatea afirmatiilor de baza din medicina sunt suficient de clare, lamurite si întelese, prea putin ne dam seama ca, de fapt, majoritatea lor sunt numai de natura statistica si ca trebuie bine nteles interpretate ca atare. Desigur, a spune ca omul are doua emisfere cerebrale sau ca ciclul cardiac are o sistola si o diastola, sunt afirmatii care nu au legatura directa cu statistica. Dar toate determinarile cantitative, unele calitative, toate masuratorile referitoare la parametri fiziologici, biochimici, biofizici etc., au înteles deplin numai în context statistic.
În medicina si stiintele vietii, afirmatiile despre mase de oameni cum ar fi populatia unei tari sau regiuni geografice sunt deseori de natura statistica. Daca exista centralizate situatii suficient de clare ale incidentei unei anumite maladii se poate face o apreciere exacta a acestei incidente. De exemplu, afectiunile maligne sunt supravegheate destul de strict în toate tarile civilizate si exista date centralizate destul de exacte asupra incidentei. Totusi, chiar si în tarile dezvoltate, dar mai ales în tarile sarace, datele sunt lacunare, în ceea ce priveste incidenta reala, adica tinând cont si de cazurile care nu sunt luate în evidenta de medici si urmarite în evolutie. În aceste cazuri, se poate face o estimare a incidentei unor maladii prin metode statistice. Se alege un esantion reprezentativ, acesta este cercetat în totalitate si pe baza rezultatului obtinut se face estimarea la nivelul întregii populatii. Tot asa se fac în ultimul timp din ce în ce mai mult studii de piata, studii în ce priveste intentiile de vot, estimari ale dorintelor unei populatii, etc. De problemele de acest tip, se ocupa un alt capitol al statisticii, acela al inferentei bazate pe sondaje.
Atunci când vorbim de prelucrarea statistica a informatiilor, folosim expresia prelucrare a datelor". Informatiile referitoare la un pacient sau la un individ normal sau la orice alt obiect le numim Date. Numele, prenumele, vârsta, sexul, afectiunea si celelalte informatii despre un anume pacient, marimea, greutatea unui obiect, productivitatea unei plante, etc, le numim date despre acel pacient, acel obiect sau acea planta. Informatiile referitoare la mai multi pacienti sau indivizi sanatosi, sau animale de experienta, sau plante, sau alte obiecte pe care le studiem, le vom numi tot date. Când ne referim la prelucrarea informatiilor, ca scop important al statisticii, vom spune prelucrarea datelor. Când vorbim despre înregistrarea pe calculator a acestor informatii vom spune înregistrarea datelor.
Astfel, statistica are ca unul din scopuri, înregistrarea si prelucrarea datelor. Totusi, nu orice tip de înregistrare de date si orice prelucrare, tin de obiectul statisticii. Înregistrarea evenimentelor cosmice în astronomie, înregistrarea facturilor în contabilitatea unei firme, înregistrarea pozitiei unui mobil în fizica, si alte înregistrari asemanatoare, nu sunt legate de statistica si nu obliga la prelucraari de natura statistica.
În sensul cel mai larg, statistici, se refera la un evantai de procedee pentru analiza, interpretarea, reprezentarea datelor si luarea deciziilor pe baza faptelor pe care le culegem din realitate. Sensul acesta al cuvântului este acoperit de cursurile de statistica.
Al doilea sens este acela de statistica definita ca o cantitate numerica calculata pe baza datelor culese din realitate. Asa cum se va vedea în capitolele ce urmeaza, statisticile aproximeaza caracteristici ale unor populatiilor, cum ar fi media pe întreaga populatie, pe care nu o cunoastem si care trebuie aproximata pe baza datelor din realitate, pe care le avem la dispozitie la un moment dat. Datele se culeg de obicei prin studiul unei parti a populatiei, care se numeste esantion sau lot. De exemplu, media calculata luând în considerare doar indivizii dintr-un lot, se numeste statistica.
Uneori, termenul de statistica se refera la cantitati calculate nu neaparat relativ la un esantion. De exemplu, exista o statistica a performantelor unui sportiv anume, o statistica a actelor oficiale publicate de o editura, etc.
Statistica este stiinta care se ocupa cu descrierea si analiza numerica a fenomenelor de masa, dezvaluind particularitatile lor de volum, structura, dinamica, conexiune, precum si regularitatile sau legile care le guverneaza.
Volumul unui fenomen de masa se refera la amploarea lui numerica, la numarul de indivizi cuprinsi sau afectati de fenomenul repectiv. Astfel, o afectiune foarte raspîndita ca HTA (Hipertensiunea Arteriala Esentiala), este un fenomen de un volum mai mare ca o afectiune rara cum ar fi Sindromul Down.
Prin structura a unui fenomen de masa, întelegem modul în care acesta afecteaza diferite categorii de indivizi, cum ar fi în cazul studierii unei afectiuni raspîndite, structura afectarii pe sexe, rase, religii, grupe de vârsta, ocupatie, zone geografice, etc. De asemeni, structura reflecta relatiile de legatura între marimile prin care descriem fenomenul. De exemplu, în cazul studierii legaturii între starea sociala si intentiile de vot, structura presupune si descrierea diferitelor categorii de indivizi pe sexe, rase, stari sociale, ocupatie, etc, cât si legaturile între acestea si intentia de vot, exprimata numeric, în procente, etc.
Prin dinamica a unui fenomen de masa, întelegem modul cum evolueaza acesta în timp. Conexiunea fenomenelor este indicata de relatiile de legatura si, eventual, de relatiile de dependenta între ele. De exemplu, fenomene economice pot influenta evolutia incidentei unor afectiuni în cadrul unei populatii. Anumite tendinte de evolutie a incidentei unei maladii, sau de modificare a valorilor normale la pacientii cu o anumita afectiune, pot capata caracter de regularitate. Statistica este cea care pune în evidenta aceste regularitati sau legi, care sunt valabile numai la modul general, ca tendinta, nu neaparat la fiecare individ în parte. De exemplu, daca stim ca o anumita fractiune leucocitara este crescuta în alergii, nu înseamna neaparat ca fiecare alergic are acea fractiune leucocitara crescuta, ci ca exista numai o tendinta în acest sens.
Definitiile, ca cea de mai sus, sunt de natura sa ne dea o ideie abstracta despre subiectul definit si este extrem de util ca domeniul de interes sau de aplicare al statisticii sa fie mai degraba exemplificat, pentru a crea o imagine concreta. De aceea, în aceasta carte, notiunile introduse sunt mereu exemplificate pentru a crea cititorului o imagine cât mai clara, mai concreta, a notiunii respective.
Se stie ca metodele statisticii au o aplicabilitate larga, începând cu ramuri ale economiei, stiintelor biologice, în viata sociala, ca sa nu mai vorbim de stiintele tehnice, astronomie, fizica atomica, etc. Cartea de fata va pune în mod normal accent pe aplicatiile în medicina si stiintele vietii, ca reprezentând obiectul biostatisticii.
Biostatistica este stiinta care se ocupa cu aplicarea metodelor statisticii în stiintele vietii.
Astfel, toate capitolele importante ale statisticii ca: statistica descriptiva, teoria sondajelor, teoria estimatiei, teoria corelatiei, regresiile, analiza componentelor principale, capitole care vor fi studiate si în acesata carte, au aplicabilitate si în stiintele vietii ca: medicina, biologia, psihologia, sau discipline mai înguste ca biochimia, biofizica, stomatologia, fizioterapia, farmacologia, etc. Metodele cu aplicabilitate în stiintele vietii au fost impulsionate în dezvoltarea lor chiar de domeniul lor de aplicare. Astfel, capitolul statisticii care se ocupa cu studiul si estimarea supravietuirii, are o aplicabilitate larga în medicina si biologie si dezvoltarea lui a fost influentata pozitiv de acest fapt Aceasta deoarece ca medicina a avut mereu nevoie de metode mai perfectionate, pe care statistica a fost nevoita sa i le puna la dispozitie.
În multe situatii, apar confuzii între doua cuvinte care exprima discipline diferite, si anume între biostatistica si statistica medicala. Aceasta din urma, este un capitol al primeia, si anume:
Statistica medicala este stiinta care se ocupa cu aplicarea metodelor statisticii în medicina.
În aceasta carte va fi vorba în principal de statistica medicala. Totusi, titlul cartii este "Introducere în biostatistica" si de-a lungul cartii este folosit termenul de biostatistica, în traditia existenta nu numai în literatura româneasca ci si în cea occidentala. Dintre aplicatiile biostatisticii sunt tratate acelea care se refera în primul rând la medicina, fiind ocolite cele cu aplicabilitate numai în alte stiinte biologice, cum ar fi cele cu aplicabilitate numai în agricultura sau în alte stiinte.
Introducem câteva notiuni specifice cu care opereaza statistica si cu care vom lucra în capitolele ce urmeaza. Fiind o stinta care nu lucreaza cu fenomene strict deterministe, toate afirmatiile statisticii se refera nu la evenimente sau obiecte singulare ci sunt deduse prin observarea unei multimi cât mai cuprinzatoare de obiecte sau fenomene. Desigur, nu se pot face generalizari pripite din studierea unui caz sau a câtorva cazuri si este destul de clar pentru oricine ca o generalizare este cu atât mai valoroasa cu cât au fost observate un numar mai mare de cazuri. Aici însa apare problema de a face o apreciere corecta a numarului de observatii efectiv realizate, raportat la numarul posibil de observatii.
Daca ne propunem sa facem un studiu asupra unei afectiuni foarte raspândite, cum ar fi hipertensiunea arteriala esentiala (HTA), concluzii valabile nu se pot trage decât pe baza unui numar de cazuri de cel putin câteva mii sau zeci de mii, dar în cazul unei maladii rare cum sunt unele din anomaliile cromozomiale de exemplu, un astfel de numar de cazuri pur si simplu nu poate fi gasit în aria de cercetare considerata, uneori nici pe întregul glob. Oricum, în general vorbind, este bine ca, în limita posibilitatilor, studiul sa se faca pe un numar cât mai mare de indivizi.
Vom numi populatie statistica o multime de elemente care au una sau mai multe însusiri comune si care fac obiectul unei cercetari statistice.
persoanele din judetul Dolj care sufera de HTA, sau
persoanele normale dintr-o arie geografica data, sau
Populatii de indivizi umani (normali, afectati de o afectiune, expusi la un risc, etc)
Vom numi individ statistic un element al unei populatii statistice indiferent de natura acesteia.
persoana umana (individ sanatos, pacient),
Numim caracteristica o proprietate comuna tuturor indivizilor dintr-o populatie statistica data.
Caracteristicile cantitative sunt acelea care prin natura lor sunt masurabile, adica pentru care exista unitati de masura si o conventie de masurare general acceptata. În aceasta categorie intra toate constantele fiziologice, biochimice, biofizice, unele anatomice, care în general pot fi determinate prin masuratori uzuale sau de laborator: înaltime, greutate, vârsta, glicemie, calcemie, hemoglobina, numar eritrocite, forta musculara, viteza de reactie, nivel de inteligenta (QI), dar si marimile referitoare la celule, organite, sinapse, vezicule, membrane, etc. Ele sunt totdeauna exprimate cifric într-un mod precis, obiectiv.
Caracteristicile cantitative sunt si ele subîmpartite în doua categorii fundamentale:
Deci, un prim criteriu de clasificare a datelor în statistica este acela care le împarte în calitative si cantitative, iar pe cele cantitative le împarte în continui si discrete (vezi figura 1.1).
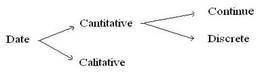
Figura. 1.1 Clasificarea cea mai generala a datelor în statistica
Astfel, majoritatea analizelor de laborator, sunt masuratori cantitative continue. Aceasta deoarece, hemoglobina sau calcemia sau glicemia, etc, pot lua orice valori între limitele de normalitate, sau chiar în afara limitelor de normalitate, iar aceste valori depind de pacientul la care s-au facut masuratorile. Atunci însa când înregistram anumite caracteristici anatomice, numarul de copii al unei paciente, numarul de nasteri, numarul de avorturi, folosim pentru înregistrare numere întregi si spunem ca înregistram o caracteristica numerica discreta.
Lumea biologica este caracterizata printr-o mare variabilitate, acest domeniu al realitatii find de fapt cel mai greu de cuprins în cifre foarte exacte, iar atunci când se obtin astfel de cifre, diferentele individuale pot fi atât de accentuate încât trebuie sa manifestam o mare reticenta în folosirea lor bruta, imediata. Desi sunt unele aspecte care se mentin constante la o aceeasi specie, si în particular la om, unele se schimba de la individ la individ, adica sunt variabile. Asadar, atunci când indivizii statistici sunt oameni, caracteristicile care se studiaza sunt de multe ori variabile. De fapt, acelasi lucru se poate spune si când indivizii sunt grupuri umane, evenimente, etc, adica se constata aceeasi variabilitate de la individ la individ.
O caracteristica care se schimba de la individ la individ sau la acelasi individ în timp sau ca raspuns la conditiile de mediu, de boala de medicatie, etc, se numeste variabila.
În aceasta carte, vom opera îndeosebi cu variabile. O valoare numerica care se obtine printr-o masuratoare pe un pacient sau în general pe un individ statistic, este de obicei o variabila si are valori cuprinse de regula între anumite limite naturale. Ceea ce este important la aceste variabile sunt doua aspecte:
Bineînteles ca, daca o caracteristica nu se schimba de la individ la individ, se numeste constanta. Constatntele nu sunt obiectul de studiu al statisticii. Acest fapt nu saraceste prea mult obiectul de studiu al statisticii medicale, deoarece putine sunt acele caracteristici ale organismului uman care sa fie cu adevarat constante.
1.5.2. Variabilitate
Medicina este stiinta care trebuie sa puna ordine într-un ocean de variabilitate. Cauzele care conduc la date de o variabilitate mai mica sau mai mare sunt atât obiective cât si subiective. Variabilitatea contine atât variatiile biologice normale si patologice cât si variatiile datorate procesului de masurare si variatii întâmplatoare carora nu li se pot da explicatii logice.
Variatia valorilor unui parametru la un acelasi individ la momente diferite de timp este variatie intrainidividuala. Se poate datora unor modificari fiziologice sau patologice care sunt legate de evolutia în timp a organismului.
Exhaustive (fiecare individ apartine unei singure clase)
Exhaustive (fiecare individ apartine unei singure clase)
Precizam aici o proprietate fundamentala a datelor de tip nominal si anume aceea ca simbolurile prin care sunt denumite categoriile sub care înregistram datele nu sunt critice, ele ar putea în principiu sa fie schimbate fara a afecta fundamental structura datelor. Sa revenim pentru aceasta la exemplul grupelor sanguine, la care dupa cum se stie uneori folosim simbolurile 0, A, B, AB, pentru a denumi grupele. În limbajul curent, folosit mai ales de nespecialisti, simbolistica intrata în uz este 0I, AII, BIII, ABIV. Acest lucru nu împiedica cu nimic o buna întelegere si chiar am putea schimba oricând aceste simboluri fara ca frecventele observate într-un grup de pacienti sa se schimbe (cu conditia bineînteles ca lumea medicala sa accepte si aceste noi simboluri). Ordinea în care apar citate aceste simboluri nu este fundamentala, este doar o problema de obisnuinta. Poate doar grupele 0I ca donator universal sau ABIV ca primitor universal au cumva locul 1 si 4 ca naturale.
Daca însa grupam pacientii dupa culoarea ochilor, dupa temperament, dupa consistenta ficatului, culoarea urinei, motivul internarii, afectiunea de care sufera, atunci simbolurile sau prescurtarile pe care le folosim au doar importanta data de uzul comun sau de conventiile internationale, sau de ordinea obisnuita numai în clinica, spitalul, orasul respectiv, neavând importanta ordinea în care le asezam atunci când facem o clasificare a lor.
1.6.2 Date alfanumerice sau literale
Tabelul 1.3. Modul de înregistrare a unor date despre pacienti (nume fictive)
În câmpul H.A.V. se observa ca au fost înregistrate doar doua posibilitati: Y(da) = "pacientul a suferit de H.A.V. în trecut" si N(nu) pentru ceilalti. În multe programe de calculator este indicata folosirea lui "Y" si"N" în loc de "da" si "nu" (Y=yes, N=no, din limba engleza), deoarece aceste câmpuri sunt considerate de program câmpuri speciale, pe care noi le vom numi câmpuri de tip logic, si sunt tratate prin procedee speciale. Deci, vom numi câmpuri de tip logic, acele coloane pe care este natural ca datele sa fie introduse folosind "Da" si "Nu".
De multe ori, numarul de linii al unui tabel cu date brute, adica al unei baze de date, este atât de mare, de ordinul sutelor sau miilor, încât însiruirea elementelor unei serii de valori (de exemplu seria vârstelor), este dificila si lipsita de semnificatie. De aceea se prefera folosirea tabelelor de frecventa în care se trec valorile diferite care apar în serie, în dreptul fiecareia precizându-se de câte ori apare acea valoare, sau frecventa de aparitie, sau frecventa absoluta a acelei valori. De exemplu, din 234 de pacienti cu afectiuni hepatice grave, vârstele au fost distribuite asa cum se observa în tabelul 1.4.
Tabelul 1.4 Tabelul de frecventa a vârstelor pentru 234 de pacienti
|
Nr |
Vârsta |
Frecventa absoluta Fi |
Frecventa absoluta cumulata crescator Ficc |
Frecventa relativa fi |
Frecventa relativa cumulata crescator ficc |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Total |
|
|
|
|
Tabelul 1.5 Modul de calcul al valorilor cuprinse în tabelul de frecvente
|
Nr |
Vârsta |
Frecventa absoluta Fi |
Frecventa absoluta cumulata crescator Ficc |
Frecventa relativa fi |
Frecventa relativa cumulata crescator ficc |
|
|
|
F1 |
F1cc=F1=1 |
f1=F1/234=0.43% |
f1cc=f1/234=0.43% |
|
|
|
F2 |
F2cc=F1+F2=2 |
f2=F2/234=0.43% |
f2cc=f2/234=0.85% |
|
|
|
F3 |
F2cc=F1+F2+F3=3 |
f3=F3/234=0.43% |
f3cc=f3/234=1.28% |
|
|
|
F4 |
F2cc=F1+F2+F3+F4=5 |
f4=F4/234=0.85% |
f4cc=f4/234=2.14% |
|
|
|
F5 |
F2cc=F1+F2+F3+F4+F5=7 |
f5=F5/234=0.85% |
f5cc=f5/234=2.99% |
|
|
|
F6 |
Etc. |
Etc. |
Etc. |
Se observa ca prin împartirea frecventelor de aparitie ale vârstelor la numarul de pacienti, se obtin frecventele relative care se exprima de obicei în procente.
Frecventele relative se calculeaza cu formula:
Este clar ca prin adunarea frecventelor absolute, se obtine numarul total de indivizi din tabel, în cazul nostru 234:
De asemeni, prin adunarea frecventelor relative (sau valorilor lor exprimate în procente), se obtine 1 (sau 100%):
În acest caz, cunoscând frecventle absolute, calculul mediei este facilitat pentru ca în loc de adunarea tuturor vârstelor, se poate calcula suma lor prin înmultirea fiecarei vârste care apare în tabel cu numarul de aparitii si apoi se aduna rezultatele. În cazul de mai sus sunt 46 frecvente absolute, corespunzatoare celor 46 vârste întâlnite între cei 234 de pacienti. Ele se noteaza cu F1, F2,.....,F46. Notând si vârstele din cele 46 linii cu x1, x2,.....x46, media vârstelor celor 234 de pacienti este:
În general, formula aceasta de calcul se numeste formula de calcul a mediei ponderate (vezi capitolul al doilea, indicatorul statisitc medie). Daca stim ca valorile x1, x2,.....xm, se repeta fiecare cu frecventele absolute F1, F2,.....,Fm, media este:
Pe ultima coloana a tabelului de frecvente, apar asa-numitele frecvente relative cumulate crescator (ficc). Frecventa relativa cumulata crescator, de pe o anumita linie, este suma frecventelor relative din celulele din coloana frecventelor relative, suma facându-se de la începutul tabelului si pâna la linia pe care se afla frecventa pe care o calculam.
Astfel, vom avea pentru frecvente relative cumulate crescator, formulele:
Tabelul 1.5 Tabelul de frecventa a vârstelor, pe grupe de vârsta de 10 ani,
pentru 234 de pacienti.
|
Nr. |
Clasa |
Fi |
Ficc |
Ficd |
fi |
ficc |
ficd |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Total |
|
|
|
|
|
|
Sa urmarim mai întâi cele câteva coloane noi care au aparut si sa încercam sa le subliniem la fiecare din ele utilitatea. Mai întâi sa amintim ca Fi, reprezinta frecventele absolute, sau numarul de indivizi care au vârstele cuprinse în limitele claselor respective. Ficc, sunt frecventele absolute, cumulate crescator, adica se obtin dupa formulele:
De exemplu, F4cc = F1 + F2 + F3 + F4 = 5+6+9+26=46, asa cum se poate vedea în linia a patra a tabelului, pe coloana a patra. Sa remarcam ca aceste frecvente cumuleaza frecventele tuturor claselor, pâna la clasa curenta, si deci ele raspund la întrebari de tipul : "câti indivizi mai tineri decât 45 de ani sunt în seria de vârste"? Raspunsul se cauta în dreptul clasei 40-45 ani, adica în a patra clasa, pe coloana Ficc : 46.
Frecventele de tipul Ficd au o semnificatie analoga, cu diferenta ca se cumuleaza descrescator, la fiecare noua clasa se scade frecventa absoluta a clasei precedente, initial plecându-se de la numarul total de indivizi din lot, în acest caz, 234.
Frecventele relative fi, sunt, asa cum am mai precizat, procentele fiecarei clase, luând întregul lot ca 100%, si se obtin ca raportul între frecventele absolute si numarul total de indivizi din lot, apoi fiind înmultite cu 100 pentru a se obtine procente. Frecventele ficc si ficd, sunt obtinute pe acelasi principiu ca si Ficc si Ficd, cu diferenta ca s-au cumulat crescator si respectiv descrescator, frecventele relative si nu cele absolute.
În sfârsit, câteva cuvinte despre intervalele care constituie clasele. Dupa cum se observa, din cauza faptului ca nu s-au înregistrat vârste decât numere întregi, clasele au o lungime usor de stabilit în mod natural: 25-30, 30-35, etc. În cazul variabilelor la care înregistrarea se face cu una sau doua zecimale, se obisnuieste ca acest lucru sa se reflecte în modul de alcatuire a claselor prin faptul ca se ia la dreapta intervalului una sau doua zecimale egale cu 9: [13 - 13,9]; [14 - 14,9]; etc pentru înregistrarea hemoglobinei, sau intervale care se termina în 99, sau chiar 999 pentru alte variabile. Strict matematic, acest mod de lucru nu este foarte corect, desi este foarte practic. Poate sa apara un caz în care într-o baza de date s-au prevazut intervalele [13 - 13,9] si [14 - 14,9] si dupa un timp ceva mai lung, aparate mai specializate sa dea un rezultat la o analiza de 13,92, care nu este încadrabil în nici una din clase. Corect este ca, de exemplu, o clasa sa fie reprezentata printr-un interval închis la stânga si deschis la dreapta, caz în care orice valoare ar apare ea este încadrabila în exact una din clase. De exemplu, daca hemoglobina la o serie de valori este cuprinsa între 9,6 si 15,9, clasele din 1 în 1 ar fi: [9 - 10), [10 - 11), [11 - 12), [12 - 13), [13 - 14), [14 - 15), [15 - 16). În acest fel, fiecare valoare din serie va intra exact în una din clase (intervale). Prima dintre clase, clasa [9 - 10), nu contine si valoarea 10, care este continuta de clasa urmatoare, si tot asa pentru fiecare clasa.
Intervalele trebuie sa acopere complet plaja posibila de valori ale variabilei si trebuie alese de asa maniera încât numarul de clase care rezulta sa nu fie nici prea mare nici prea mic, astfel ca aprecierea modului cum sunt datele distribuite sa fie cât mai usoara. Este recomandabil ca numarul de intervale pentru un astfel de tabel statistic sa fie de la câteva, pentru loturi de câteva zeci de indivizi, pâna la câteva zeci, daca lotul este foarte mare, de mai multe sute sau mii de indivizi.
De obicei, programele de calculator realizeaza aceste tabele dupa ce utilizatorul a furnizat lungimea clasei. Pentru a nu ajunge în situatii când un astfel de tabel are un numar total neindicat de clase, de obicei se calculeaza lungimea unei clase în asa fel încât numarul de clase sa fie cel dorit. Acest lucru se poate realiza daca se cauta cea mai mica si cea mai mare valoare din seria de date (notate mai jos cu min si max), si se ia ca lungime a unei clase, aproximativ rezultatul urmatorului calcul:
![]()
De exemplu, pentru tabelul de mai sus, cel mai tânar pacient are 26 de ani, iar cel mai vârstnic are 78, deci pentru a obtine 6 clase (numar de clase indicat pentru vârste de adulti), avem L= (78 - 26) / 6 = 8,6. Deci este indicat sa se ia clase de 10 ani, prin rotunjire. Daca însa se doresc mai multe clase, sa zicem 10, atunci obtinem: L = (78 - 26) / 10 = 5,2 si este indicat sa se ia clase din 5 în 5 ani. Prima clasa va fi [25,30), iar urmatoarele: [30, 35), [35, 40),.
Numarul de clase nu este neaparat 10, el se alege de fapt de catre cel care face calculul, astfel ca sa se piarda cât mai putina informatie, dar si numarul de clase sa nu fie prea mare caci atunci luam în considerare aspecte prea nesemnificative.
Ca regula generala, este bine sa se retina ca:
Întrucât cei care nu au experienta nu stiu cum sa aleaga numarul de clase, recomandam:
Nu se recomanda folosirea a mai mult de 20 - 30 de clase decât în cazuri speciale, în studii cu multe mii de cazuri. Nici mai putin de 4 - 6 clase nu este recomandat sa se foloseasca. Nu se recomanda folosirea acestor tabele daca nu avem cel putin câteva zeci de valori. De exemplu, pentru o serie de 15 valori, nu se face un tabel de frecventa.
Alte exemple:
Daca avem de clasificat într-un tabel de incidenta valorile pentru hemoglobina, iar minimul este 8,13 iar maximul este 16,23, atunci, pentru a obtine 10 clase, vom face calculul:
În acest caz, vom rotunji la 1 si vom lua clasele din 1 în 1, începând de la 8: [8, 9), [9,10), [16,17).
În cazul Imunoglobulinei G, din cei 235 de pacienti din acelasi lot ca cel pentru vârste de mai sus, valoarea minima a fost 112, în timp ce maximul a fost 900. Daca dorim tot 10 clase, atunci calculul este
Vom lua clasele din 100 în 100, începând de la 100: [100,200), [200,300) .. [800,900), [900-1000).
Informatia sintetizata într-un astfel de tabel este deosebit de utila si este de multe ori completata prin reprezentarea grafica a ei care se face cu ajutorul histogramei. Se poate spune ca sintetizarea informatiei continuta de o serie de valori într-un tabel de frecventa, este primul pas în studiul datelor brute, adica asa cum au fost inregistrate. Aceasta "distilare" a valorilor se face cu o pierdere de informatie, dar ofera o imagine sintetica pe care nu o putem avea prin simpla trecere în revista a valorilor din serie. Metodele statistice au în general aceasta calitate, aceea ca, în schimbul pierderii de informatie care uneori este nesemnificativa, ofera mai multa claritate prin sintetizarea acestei informatii si scoaterea în evidenta a caracteristicilor esentiale ale seriei sau seriilor de valori pe care le avem de studiat.
2.1 Serii de valori
Asa cum s-a vazut în capitolul anterior, uneori este necesar sa urmarim mai întâi un singur parametru numeric din multitudinea de parametri înregistrati într-un tabel de date. În acest caz, datele numerice pe care le avem la dispozitie sunt un simplu sir de numere asociate, fiecare din ele, unui individ. Întrucât aprecierile asupra întregului sir de numere nu au în acest caz nici o legatura cu situatia fiecarui individ în parte, asocierea între indivizi si valorile corespunzatoare îsi pierde interesul si trebuie avut în vedere doar sirul de numere rezultat. Este adevarat ca uneori este necesar sa se tina seama de ordinea în care apar valorile într-un astfel de sir, ca în cazul asa numitelor serii temporale la care masuratorile sunt luate într-o anumita ordine, dar de obicei ordinea este neimportanta si în cele ce urmeaza vom considera ca suntem în acest caz, în care ordinea este neinportanta. Aceste siruri de numere rezultate din datele culese le vom numi serii statistice sau serii de date sau serii de valori.
Ceea ce trebuie urmarit în primul rând la o serie de valori este modul în care valorile din serie sunt distribuite în plaja de valori între un minim si un maxim, cum se distribuie în jurul mediei, care este tendinta centrala a seriei, care sunt valorile cel mai des întâlnite, etc.
Caracterizarea sintetica a unei serii de valori este data de asa numitii indicatori statistici, între care media, deviatia standard, mediana, etc, indicatori pe care îi vom descrie în continuare.
Indicatorii statistici sunt numere reale, care sintetizeaza o parte din informatia continuta de o serie de valori, dând posibilitata aprecierii globale a întregii serii, în loc sa tinem cont de fiecare valoare din sir. Asa cum se va vedea în acest capitol, fiecare indicator urmareste sa scoata în evidenta proprietati diferite ale sirului de valori. Astfel, prin combinarea mai multor indicatori, obtinem informatii relevante si sintetice despre valorile sirului. Daca în locul sirului propriu-zis, folosim o serie de indicatori statistici, o parte din informatie se pierde. Totusi, de obicei se pierde ceea ce este nesemnificativ, accidental, indicatorii statistici retinând doar esentailul. De aici si utilitatea si importanta lor în statistica.
În cele ce urmeaza, valorile din sirul de numere ce constituie o serie de valori le vom nota cu
X: x1, x2,....... xn, sau Y: y1,y2,...yn
sau notatii asemanatoare folosind alte litere ale alfabetului.
De exemplu, în loc sa spunem ca cele 10 valori ale glicemei la cei zece pacienti dintr-un lot sunt: 88, 97, 103, 89, 93, 105, 98, 105, 88, 103, vom scrie în loc de Glicemie litera X, si în locul fiecarui numar din cele zece, simbolurile x1, x2,..x10. Deci, x1 tine locul lui 88, x2 pe cel al lui 97, etc. Aceste notatii le folosim pentru a usura întelegerea formulelor de calcul pentru unii indicatori.
2.2 Indicatori statistici
2.2.1 Valori extreme, amplitudine
2.2.2. Valori medii
Media aritmetica a unei serii de valori. Este un indicator simplu si în acelasi timp foarte sintetic, fiind un foarte bun indiciu al valorii în jurul careia se grupeaza datele. Se noteaza cu litera m sau, daca seria de valori este notata cu o majuscula ca X sau Y, media se noteaza cu sau . Formula este cea cunoscuta:
Media aritmetica unei serii de valori este raportul dintre suma valorilor seriei si numarul lor.
Iata câteva din proprietatile fundamentale ale mediei:
Media calculata cu formula de mai sus se numeste media aritmetica, pentru a o deosebi de alte tipuri de medii cum ar fi media geometrica sau media armonica. Media aritmetica este cea mai importanta dintre medii si cea mai folosita în practica. De aceea, de obicei i se mai spune simplu medie.
Media este indicatorul care arata tendinta centrala a seriei de valori, si de obicei arata unde tind datele sa se aglomereze. De cele mai multe ori, valorile din serie sunt situate în majoritate în apropierea mediei, iar o mai mica parte din ele sunt situate mult în stânga sau în dreapta mediei. O situare a valorilor din serie fata de medie se poate observa din asa-numitul grafic punctual de dispersie, din care este dat un exemplu în figura 2.2
Figura 2.2. Cele mai multe valori sunt de obicei mai apropiate de medie.
Dar nu totdeauna datele din seria de valori se situeaza preponderant în apropierea mediei. Mai rar, si oarecum mai fortat, ne putem întâlni si cu situatii în care datele din serie se situeaza preponderant în stânga si dreapta, departe de medie si doar o mica parte dintre ele se situeaza aproape de medie, asa cum se observa în figura 2.3.
Figura 2.3. Uneori, cele mai multe valori sunt sub medie si peste medie, destul de departe de aceasta. În seriile de mai sus, avem aceeasi medie, dar este evident ca nu avem aceeasi situatie. Valorile din seria de jos sunt mai împrastiate.
Astfel, daca în acelasi lot sunt cuprinsi indivizi hipertiroidieni si hipotiroidieni, si se masoara la fiecare concentratia hormonului tiroidian T4, vom observa ca hipotiroidienii au preponderent valori în stânga mediei, cei mai multi destul de departe de medie, iar hipertiroidienii au preponderant valori în dreapta, tot departe de medie. De fapt într-un asemenea caz, în zona centrala lipsesc exact ceea ce am spune ca sunt normalii, adica indivizi care au valori pentru T4 usor peste si sub medie, si care nu au fost inclusi într-un astfel de lot. Evident ca un esantion asa de eterogen nu este folosit prea des în statistica pentru ca, asa cum vom vedea, în acest caz este foarte indicat sa se constituie doua esantioane distincte pentru cele doua categorii de pacienti. Totusi, asemenea situatii, chiar daca de obicei nu sunt indicate si sunt putin artificiale, exista. Situatia de mai sus este ilustrata în figura 2.3.
Vom nota cu media unei serii de valori X.
Pentru seriile X si Y de mai sus mediile , si sunt:
Am folosit pentru medie si
notatia ![]() pe care o vom folosi de acum înainte. Notatia m are dezavantajul ca daca se
lucreaza cu doua serii de valori odata, trebuie folositi
indici pentru a deosebi cele doua medii, de aceea vom folosi în cele ce
urmeaza cealalta notatie.
pe care o vom folosi de acum înainte. Notatia m are dezavantajul ca daca se
lucreaza cu doua serii de valori odata, trebuie folositi
indici pentru a deosebi cele doua medii, de aceea vom folosi în cele ce
urmeaza cealalta notatie.
Se observa ca introducerea celor 4 pacienti în plus în seria Y, fata de cei 10 pe care îi contine si seria X, modifica destul de mult media, din cauza valorii 46, care este mult mai mica decât celelalte. Deci, media este un indicator sensibil la introducerea sau înlaturarea unor valori extrem de mari sau de mici.
O formula simplificata pentru media aritmetica este data de (vezi cap. 1.9):
unde cu n am notat numarul de valori diferite din seria de valori, iar F1, F2, ... Fn sunt frecventele de aparitie în serie ale valorilor x1, x2, ... xn
Aceasta formula se spune ca este formula pentru media ponderata, ceea ce este gresit, dar expresia a intrat în uz si este folosita curent, de aceea o vom folosi în aceasta carte. Nu trebuie sa credem ca media ponderata calculata cu formula de mai sus si media aritmetica calculata cu formula (2.1), sunt indicatori diferiti. Ambele medii sunt în realitate identice. Media ponderata se calculeaza de obicei mai simplu si deci nu reprezinta decât o forma mai simpla de calcul al mediei aritmetice.
Prin faptul ca este un indicator extrem de fidel al tendintei centrale al unei serii statistice, media este un indicator statistic extrem de mult utilizat în statistica. Media aritmetica are dezavantajul ca este sensibila la valori extreme fie foarte mici, fie foarte mari. Adaugarea unei singure valori (sau a câtorva) mult mai mari decât celelalte, modifica sensibil media aritmetica.
De asemenea, daca datele sunt distribuite în jurul mediei puternic asimetric, media îsi pierde din puterea de a evoca tendinta centrala, în aceste cazuri fiind mult mai utila mediana (vezi mai jos).
De exemplu, în figura 2.4, se observa ca cele mai multe valori din cele 233 ale seriei reprezentate în grafic (viteze de sedimentare a hematiilor la o ora), sunt aglomerate în primele patru bare din stânga, adica în stânga mediei, care este 40,57. În acest caz, media nu arata locul unde se aglomereaza mai mult datele din serie si îsi pierde o parte din utilitate. A se vedea mai jos, indicatorul mediana si de ce în acest caz este mai util decât media.
Fig. 2.4 Daca datele se distribuie asimetric, media (40,54) nu mai arata tendinta centrala. Majoritatea valorilor sunt în stânga mediei (156 în stânga, 77 în dreapta). Cele mai multe valori din serie sunt în intervalul 10 - 30, deci nu în jurul mediei.
2.2.3 Împrastiere
Abaterea medie se obtine facând media aritmetica a acestor abateri absolute luate cu semnul plus, adica în modul. Aceasta este un indicator al împrastierii valorilor din serie dar nu este aproape deloc folosita în practica, pentru ca, asa cum se va vedea în capitolul despre teste statistice, un alt indicator al împrastierii, dispersia, este mult mai utila.
Formula pentru abaterea medie este:
Dispersia. Un alt mod de a ocoli faptul ca suma abaterilor absolute este 0, este ridicarea la patrat a acestora înainte de a fi adunate, pentru a face sa dispara semnele negative la unele si pozitive la altele. Suma obtinuta, ar trebui împartita la numarul de abateri pentru a se obtine o medie. În realitate, din motive teoretice foarte bine întemeiate, dar mai greu de explicat în cuvinte simple, împartirea se face la n-1 si nu la n. Motivul pentru care se face acest lucru va fi înteles mai bine în contextul unor notiuni enuntate în capitolul despre teoria estimatiei. Valoarea care se obtine astfel se numeste dispersie si este un indicator al gradului de împrastiere al seriei. Dispersia se noteaza cu D si are formula:
Dupa cum se observa, numaratorul fractiei din definitia dispersiei este cu atât mai mare cu cât abaterile individuale de la medie sunt mai mari si deci este natural sa consideram ca o valoare mare a dispersiei arata o împrastiere mare a valorilor din serie.
De fapt, este bine de retinut ca:
Dispersia are dezavantajul ca se exprima cu unitatile de masura ale valorilor din serie, ridicate la patrat, si are în general valori foarte mari comparativ cu abaterea medie. De exemplu, daca valorile din serie se masoara în mg/l, atunci dispersia se masoara în mg2/l2, ceea ce este în mod evident extrem de nenatural. În plus, daca abaterile absolute au o medie, de exemplu în jurul lui 10, dispersia va avea o valoare în jurul lui 100, adica exagerat de mare în comparatie cu abaterile absolute (vezi pagina urmatoare pentru exemple). De aceea se mai foloseste un alt indicator, numit abatere standard care este radicalul dispersiei.
Abaterea standard. Se noteaza cu s si are formula:
sau
Acest indicator se exprima cu aceeasi unitate de masura ca si valorile din seria considerata si este un indicator foarte fidel al împrastierii seriei.
Exemplu de calcul:
Sa presupunem ca am masurat zilnic tensiunea arteriala sistolica la doi pacienti timp de 10 zile, obtinând pentru fiecare urmatoarele valori:
Lasând la o parte studiul modului cum evolueaza de la zi la zi tensiunea pacientilor, care este bineînteles importanta, sa ne propunem sa determinam care are tensiunea cu valori mai împrastiate, indiferent de evolutia în timp.
Notând prima serie cu X iar pe a doua cu Y se constata usor ca ambele au media 180 (datele nu sunt reale, au fost deliberat alese ca sa simplifice calculele). Atunci, vom avea pentru abaterile de la medie si pentru patratele lor urmatoarele valori:
Deci vom avea pentru Dx:
si cu un calcul absolut analog, Dy = 1600 / 9 = 177,7. Se observa ca, în timp ce abaterile de la medie sunt de ordinul zecilor, dispersiile sunt de ordinul sutelor, ceea ce este destul de nenatural, si în plus, dupa cum am mai spus, unitatea de masura este cu totul alta.
Pentru abaterile standard, vom avea:
calculele fiind facute cu aproximatie. Deci, este mai împrastiata seria Y.
De fapt, este bine de retinut ca:
Ce se întampla însa daca mediile si deviatiile sunt foarte diferite? Atunci o buna apreciere se obtine daca se foloseste raportul deviatiei standard fata de medie, exprimat în procente, acest raport fiind un alt indicator al împrastierii valorilor dintr-o serie. Acest indicator se numeste coeficient de variatie.
Coeficientul de variatie. Este raportul dintre deviatia standard si medie, atunci când media este diferita de 0 si se exprima în procente:
Pentru seriile de mai sus, coeficientul de variatie este mai mare pentru cea mai împrastiata, adica pentru cea cu deviatia standard mai mare:
Totusi, seriile de mai sus sunt comparabile cu ajutorul abaterilor standard, deoarece au aceeasi medie, si, asa cum s-a vazut, la medii egale sau aproximativ egale, are valorile mai împrastiate seria cu abaterea standard mai mare.
Aprecierea cu ajutorul coeficientului de variatie se face mai ales atunci când doua serii de valori au medii mult diferite si deviatiile standard pot sa nu ne dea o indicatie suficient de utila. De exemplu, masurând latenta si amplitudinea semnalului electric pe nervul optic la 120 de pacienti cu scleroza multipla, s-au obtinut urmatoarele rezultate:
Daca dorim sa apreciem împrastierea valorilor din cele doua serii, abaterile standard nu ne sunt de ajutor. Într-adevar, latenta are o abatere standard mult mai mare decât amplitudinea, dar si media latentei este cu mult mai mare decât aceea a amplitudinii. De aceea, în acest caz, doar coeficientul de variatie ne permite o apreciere corecta a împrastierilor, în vederea compararii lor:
Se observa ca valorile amplitudinii sunt cu mult mai împrastiate decât cele ale latentei. Acest fapt se datoreaza atât unei variabilitati biologice mai mari la amplitudine decât la latenta, cât si unei variabilitati datorate aparatelor de masura, care masoara latenta cu mai multa precizie, în timp ce la masurarea amplitudinii, erorile de masurare sunt mai mari.
Coeficientul de variatie este cel mai fidel indicator al împrastierii unei serii statistice, dar are si el un inconvenient, este cu atât mai fidel cu cât mediile sunt mai departate de 0.
Observatie: deviatia standard este posibil sa fie mai mare decât media si ca atare se pot obtine coeficienti de variatie mai mari decât 100%. Depasirea procentului de 100%, la o anumita serie de valori, este un semn al faptului ca C.V. reflecta mai putin fidel împrastierea.
2.2.4 Indicatori de asimetrie
Atunci când valorile unei serii sunt distribuite nesimetric în jurul mediei, acest fapt este imposibil de surprins cu ajutorul indicatorilor de dispersie. De aceea, s-au introdus indicatori care sa puna în evidenta si acest aspect al seriilor de valori: excentricitatea, sau asimetria. Va trebui sa tinem cont atât de numarul de valori care sunt în stânga si în dreapta mediei, cât si departarea lor fata de medie.
Mediana
Mediana este acea valoare dintr-o serie de valori, pentru care exact jumatate din ele sunt mai mici decât ea, iar jumatate mai mari
Altfel spus, este valoarea masurata pentru individul din mijloc, daca indivizii pe care s-au facut masuratorile ar fi ordonati creascator. Pentru o întelegere mai usoara, sa luam un exemplu cu numai 10 înregistrari: tensiunea arteriala maxima la un bolnav în 10 zile:
Daca se asaza aceste valori într-un sir crescator, obtinem:
În acest caz, mediana se ia între a cincia si a sasea valoare din acest sir ordonat, adica 160. Daca aceste doua valori de mijloc difera, se ia media lor aritmetica. Daca numarul de masuratori este impar atunci madiana este chiar valoarea de mijloc, care în acest caz este unica.
De fapt, mediana este importanta în primul rând la serii de valori cu mai multe înregistrari, caz în care se poate lucra direct pe tabelul de frecventa, sau chiar pe tabelul pe clase.
Pentru a exemplifica modul cum se cauta mediana pe tabelul de frecventa, vom lua tabelul 2.1, în care sunt centralizate vârstele a 234 de pacienti, fiecare valoare a vârstei având o anumita frecventa absoluta Fi, o frecventa relativa fi si o frecventa relativa cumulata crescator, ficc (vezi subcapitolul 1.9, pentru amanunte).
Tabelul 2.1. Vârstele a 234 de pacienti centralizate într-un tabel de frecventa
Tabelul 2.2 Vârstele a 229 de pacienti, grupate pe clase din 10 în 10 ani
|
Nr. Clasei |
Interval (ani) |
Fi |
Ficc |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Deoarece în total sunt 229 de înregistrari ale vârstelor pentru cei 229 de pacienti valoarea din mijloc este a 115-a (114 vor avea vârste mai mici, iar ceilalti 114, mai mari, daca îi ordonam crescator). Din frecventele absolute cumulate crescator, se vede ca înregistrarea cu numarul 115 este în clasa a 4-a, între 50 - 59 de ani. Pentru un calcul aproximativ, trebuie aplicata regula de trei simpla si anume, daca înregistrarile ar fi ordonate crescator nu numai pe clase ci si în interiorul unei clase, atunci putem spune ca: ultima înregistrare din clasa 3 are 49 de ani si este a 70-a. În clasa a 4-a, prima înregistrare are 50 de ani si este a 71-a, iar ultima are 59 de ani si este a 166-a. Deci:
La ce vârsta va corespunde înregistrarea 115? Sa notam cu x aceasta vârsta necunoscuta, care este de fapt chiar mediana. Deci, de la locul 115 la 166, avem o crestere de vârsta de 59-x ani, iar de la locul 71 la 115, avem o crestere de x-50 ani. Cele doua cresteri de vârsta, sunt proportionale cu numarul de locuri:
Aceasta ecuatie simpla se rezolva scriind ca produsul mezilor este egal cu produsul extremilor, deci:
(166 -115) (x-50) = (115 - 71) (59-x) sau
51 x - 2550 = 2596 - 44 x sau
95 x = 5146 de unde se obtine
x= 5146 / 95 = 54 ani, aproximativ.
De obicei, valorile obtinute din astfel de calcule sunt cu zecimale, dar ele trebuie rotunjite pentru ca, oricum, calculele sunt aproximative, cresterea de vârsta nefiind aceeasi de la loc la loc, asa cum se presupune când se scriu rapoartele de proportionalitate.
Mediana este un indicator al tendintei centrale, ca si media, dar ofera mai putina informatie decât aceasta din urma. La distributiile echilibrate, la care valorile din serie se dispun aproximativ simetric în stânga si în dreapta mediei, media si mediana sunt foarte apropiate, deci folosirea medianei este superflua. Daca însa mediana este mult în stânga sau în dreapta mediei, distributia se zice ca este excentrica.
De exemplu, venitul median este mai informativ decât venitul mediu deoarece distributia veniturilor într-o populatie este foarte excentrica. Astfel, angajatii unei firme mici ar putea avea veniturile în euro date de tabelul de mai jos:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Media venitului este 842.3 euro, iar venitul median este 80 euro. Daca apreciem venitul unui angajat al firmei, este mai informativa mediana care ne spune ca jumatate din angajati au sub 80 euro sau chiar 80 si jumatate au 80 sau mai mult.
Mediana are proprietatea ca suma deviatiilor absolute de la mediana a valorilor din serie este mai mica dacât suma deviatiilor absolute de la orice alt numar. Mediana este mult mai putin sensibila la variatiile introduse în serie de aparitia câtorva valori extreme foarte mari sau foarte mici. Acesta este un avantaj dar si un dezavantaj si o face sa fie preferata mediei în cazul distributiilor asimetrice.
Cuartilele. De obicei, o distributie excentrica trebuie cunoscuta prin tendinta sa de a se apropia de axa orizontala mai brusc sau mai lent (vezi figura 2.4, unde cresterea înaltimii barelor se face brusc, iar scaderea mult mai lent). De un real folos în aceasta directie ne pot fi indicatorii numiti cuartile.
Cuartila Q1 este acea valoare dintr-o serie de valori, pentru care 25% din valorile seriei sunt sub Q1 si 75%, peste
Pentru tabelul de frecvente 2.1, cuartila Q1 se cauta în dreptul frecventei relative cumulate crescator de 25%. În tabel gasim procentul de 24,4% si în dreptul lui vârsta de 47 de ani. Cuartila Q1 poate fi luata cu aproximatie 47. Pe tabelul cu frecvente pe clase 2.2, un calcul analog cu cel de la mediana, dar nu pentru îndividul 155 ci pentru individul 58 (57*4=228, si sunt 229 înregistrari), da pentru Q1 valoarea 46,9 ani si trebuie luata prin rotunjire 47 ani.
Cuartila Q3 este acea valoare dintr-o serie de valori, pentru care 75% din valorile seriei sunt sub Q3 si 25%, peste
Pentru tabelul 2.1, cuartila Q3 se ia din dreptul frecventei relative cumulate crescator de 75%. Poate fi luata cu aproximatie, 60 ani. Pentru tabelul 2.2, Q3 este corespunzatoare individului 172 (57*4=228, sunt 229 înregistrati, iar 57*3= 171). Dupa calcule asemanatoare se gaseste Q3= 60,8 ani si se ia prin rotunjire 61 ani.
Pentru a sublinia utilitatea indicatorilor Q1 si Q3, sa consideram sirul vârstelor:
cel mai tânar pacient,
Q1,
mediana,
Q3,
cel mai în vârsta pacient.
Pentru tabelul 2.2, obtinem sirul: 26 ani, 47 ani, 54 ani, 61 ani, 69 ani.
Minim
Cuartila Q1
Mediana
Cuartila Q3
Maximum
|
Nr |
Valoarea |
Decila |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Modul cum arata decilele simetria sau asimetria valorilor dintr-o serie de valori, poate fi urmarita în figurile 2.5, 2.6, 2.8 si 2.9.
Se oserva în figura 2.6 ca dispunerea celor 9 decile este extrem de simetrica de la stânga la dreapta, ceea ce spune ca distributia valorilor din serie este foarte simetrica. În figura 2.9, dispunerea decilelor este foarte asimetrica, descriind bine asimetria valorilor din serie.
Centilele (percentilele) sunt mai rar folosite, în studii pe mii de cazuri, de obicei de un interes mai larg, national, international, în studii epidemiologice, si sunt corespunzatoare precentelor de 1%, 2%,...99% din lot. Centila de 25% este cuartila Q1, cea de 50% este mediana, iar cea de 75% este cuartila Q3. Centilele de 10%, 20%,..90%, sunt cele noua decile. Centilele dau o imagine destul de exacta a distributiei valorilor dintr-o serie de valori foarte mare. Nu are rost sa calculam centile pentru serii cu câteva sute de valori, pentru ca erorile sunt prea mari si imaginea obtinuta este deformata.
2.2.5 Alti indicatori statistici
Eroarea standard Este indicatorul care arata cât de precis aproximeaza media calculata din valorile unei serii, media populatiei din care a fost extras esantionul sau lotul pe care s-au facut masuratorile.
Are formula:
unde este deviatia standard calculata folosind valorile seriei, iar n este numarul de valori din serie.
Se observa ca este direct proportionala cu deviatia standard a valorilor din serie si deci, cu cât valorile din serie sunt mai dispersate, cu atât valoarea indicatorului Err va fi mai mare. Proportionalitatea este directa, adica o crestere a deviatiei standard, conduce la o crestere proportionala a lui Err.
Valoarea lui Err, este influentata dupa cum se vede din formula si de numarul de valori din serie, în sensul ca, este cu atât mai mica cu cât sunt mai multe valori în serie, daca deviatia standard nu se schimba. Err scade în functie de numarul de valori din serie, nu însa proportional.
De exemplu, daca n creste de 4 ori, Err scade de doua ori: doua serii de valori, X si Y, au aceeasi deviatie standard egala cu 2,3, iar numarul de valori în seria X este 25 iar cel al seriei Y este 100. Atunci erorile standard pentru cele doua serii sunt:
Deoarece este considerata a fi abaterea standard a mediei (calculata pe valorile masurate pe un lot), fata de media întregii populatii, i se mai spune uneori «abaterea standard a mediei de la medie», ceea ce este bineînteles un simplu joc de cuvinte si nu trebuie luat în serios atunci când este întâlnit.
Modul. Dintre frecventele absolute aparute într-un tabel de frecvente, una este maxima. Clasa sau valoarea corespunzatoare acestei frecvente maxime se numeste mod. Modul este de obicei un indicator al tendintei centrale. În tabelul 2.2. modul este clasa de la 50 la 59 de ani, cu frecventa absoluta 96. De obicei, frecventele absolute au tendinta de a creste catre mod, dupa care urmeaza o descrestere continua. Modul este deci o indicatie relativa la maximul frecventelor absolute. Sunt însa distributii la care se înregistreaza cresteri si descresteri astfel încât pot apare doua moduri sau chiar mai multe. Aceste distributii sunt mai rare si au un caracter cu totul special. Ele se numesc distributii bimodale sau multimodale,dupa caz.
Este un indicator care poarta în el putina informatie despre datele seriei. Modul este mult influentat de fluctuatii aleatoare si nu este prea recomandat pentru a aprecia tendinta centrala a valorilor dintr-o serie. Mai mult, unele distributii pot fi multimodale, caz în care modul nu mai indica prea mult despre tendinta centrala.
Excentricitate. (Engl. Skew, Skweness). Este un indicator al asimetriei si este luat de diversi autori cu diverse formule
O distributie este excentrica daca una din cozile sale este mai lunga decât cealalta. Prima distributie din figura 2.11 este cu excentricitate pozitiva. Adica are o coada mai lunga în directia pozitiva. A doua distributie este asimetrica cu asimetrie negativa, deoarece are o coada în directia negativa. În sfârsit, a treia distributie este simetrica si nu are cozi. Uneori se spune despre o distributie cu excenticitate pozitiva ca este asimetrica spre dreapta, iar despre o distributie cu excentricitate negativa ca este asimetrica spre stânga.
Figura 2.11 Distributii cu excentricitate pozitiva, negativa si distributie simetrica
Distributiile cu excentricitate pozitiva sunt mai des întâlnite decât cele cu excentricitate negativa. În medicina, parametrii fiziologici sunt în majoritate modificati în diverse afectiuni în sensul ca au valori peste normal. Astfel, tensiunea arteriala o vom întâlni la valori normale, crescute sau scazute. Cum indivizi cu valori foarte mari, vom întâlni cu atât mai rar cu cât valoarea este mai mare, distributia va avea o coada spre dreapta. La fel la multi alti parametric cum ar fi bilirubina, transaminazele, colesterolul, lipemia, etc.
Totusi, vom întâlni si parametri care se distribuie cu asimetrie stânga în patologii: hemoglobina, calcemia, sodiul ionic, etc. Hemoglobina, de exemplu, se poate distribui cu frecventa mai mare la valori relativ normale si cu frecvente din ce în ce mai mici pe masura ce coborâm la valori mai mici. Chiar daca avem o patologie de tip anemie, ne asteptam ca frecventa în jurul a 9-10 sa fie mai mare decât frecventa în jurul a 7-8, frecventa care ne asteptam sa fie foarte mica.
Excentricitatea unei serii de valori x1, x2,...xn, se calculeaza cu formula:
Cu cât o distributie este mai simetrica cu atât sk tinde la 0. Ca o regula generala, la distributiile cu excentricitate pozitiva, media este mai mare decât mediana. Evident, media este mai mica decât mediana la distributiile cu excentricitate negativa. Exista cazuri rare în care regula de mai sus nu este valabila.
Sunt multe alte formule pentru alti coeficienti de excentricitate si când vorbim despre excentriciatte, trebuie sa mentionam la ce coeficient de excentricitate ne referim. Uneori se foloseste un coeficent de asimetrie care masoara diferenta dintre medie si mediana, eventual raportata la abaterea standard sau la intervale intercuartilice( Q3 - Q1). Indiferent ce formula se foloseste, o excentricitate egala cu zero, sau foarte apropiata de zero, este un indiciu al simetriei repartitiei valorilor din serie. Din contra, excentricitati mult diferite de 0, peste 0,15 -0,20, sau mai jos de -0,15 -0,20 sunt indicii ale asimetriei.
Boltirea Boltirea este un indicator care se bazeaza pe lungimea cozilor unei distributii. Cele cu cozi relativ mari se numesc leptocurtice iar cele cu cozi relativ mici se numesc platicurtice (vezi figura 2.13). Formula de calcul a boltirii este:
Asa cum se va vedea în capitolul despre repartitii, boltirea este un indicator util în aprecierea apropierii repartitiei de repartitia normala. Distributiile din figura 2.13 au aceeasi medie, aceeasi dispersie, aproximativ aceeasi excentricitate dar difera mult ca boltire.
Figura 2.13 Distibutie leptocurtica si distributie platicurtica.
2.3 Clasificarea indicatorilor
Indicatorii statistici poarta în ei, fiecare, o anumita cantitate de informatie, din seria de valori pentru care au fost calculati. Asa cum s-a vazut în paragraful precedent, unii indicatori ne dau informatii despre tendinta centrala a valorilor din serie, altii ne dau informatii despre împrastierea valorilor, altii ne dau indicatii despre simetria valorilor din serie, boltirea ne da indicatii despre lungimea cozilor distributiei, etc.
Informatia oferita de indicatorii statistici este redundanta, în sensul ca, de exemplu, împrastierea valorilor din serie este indicata si de dispersie si de abaterea standard si de amplitudinea absoluta si de coeficientul de variatie, etc. Totusi, fiecare din ei aduce o mica informatie specifica, deci, nu ne putem lipsi de unul sau altul dintre indicatorii statistici. Uneori trebuie folositi unii dintre indicatori, fiind cei mai eficienti, alteori trebuie folositi altii.
Pentru a avea o ideie despre modul cum trebuie folositi indicatorii statistici, ei sunt clasificati în câteva categorii mai importante, categorii care vor fi exemplificate mai jos, insistând pe aceia care sunt cei mai importanti, restul fiind indicatori mai rar folositi, numai în cazuri speciale.
Indicatori ai tendintei centrale. Cei mai importanti indicatori ai tendintei centrale sunt media, mediana si modul. Media indica tendinta centrala atunci când seria de valori este repartizata simetric în jurul ei si când valorile nu au o dispersie exagerat de mare. În cazul seriilor de valori distribuite foarte asimetric, tendinta centrala nu mai este indicata de catre medie, ci de catre mediana.
Modul, este un indicator al tendintei centrale, la seriile unimodale, adica atunci când în tabelul de frecvente exista un singur maxim. Daca avem o serie multimodala, modul îsi pierde calitatea de indicator al tendintei centrale.
Indicatori ai împrastierii. Folositi mai des în practica, si deci mai importanti, sunt dispersia, abaterea standard si coeficientul de variatie.
Abaterea standard este indicatorul folosit cel mai des pentru aprecierea împrastierii, dar atunci când mediile difera mult, este mai util coeficientul de variatie. Dispersia este folosita ca masura a împrastierii în testele statistice (vezi capitolul dedicat testelor statistice).
Indicatori ai asimetriei. Mediana, cuartilele si excentricitatea sunt cel mai mult folosite pentru aprecierea asimetriei valorilor dintr-o serie. De fapt, mediana se foloseste în combinatie cu media pentru aprecierea asimetriei. O mediana mult diferita de medie indica asimetrie puternica, iar o mediana foarte apropiata de medie indica o tendinta spre simetrie.
Cuartilele, se folosesc în combinatie cu mediana si indicatorii minim si maxim, pentru aprecierea simetriei. De exemplu, asa cum se vede în figura 2.14, indicatorii minim, Q1, mediana, Q3 si maxim, împart valorile seriei în patru sferturi, care ne arata cât de asimetric sunt repartizate.
Figura 2.14 Folosirea indicatorilor minim, Q1, mediana, Q3 si maxim pentru aprecierea simetriei valorilor din seria de valori.
3. Studiul datelor nominale
3.1 Tabele de incidenta. Notiuni introductive
Datele înregistrate pe doua sau mai multe coloane si care sunt de tip nominal pot fi studiate prin asa-numitele tabele de incidenta. Cel mai simplu astfel de tabel centralizeaza date referitoare la doua caracteristici care au câte doua posibilitati. De exemplu, daca din 260 de pacienti diabetici se constata ca 86 au facut retinopatie, dintre care 29 au si nefropatie, iar din restul fara retinopatie, 2 au nefropatie, atunci aceste date pot fi sintetizate astfel:
Tabelul 3.1. Clasificarea a 260 de pacienti cu diabet juvenil, dupa prezenta sau absenta retinopatiei diabetice si a nefropatiei.
|
|
|
Nefropatie |
|
|
|
|
|
"+" |
"-" |
Total |
|
Retinopatie |
"+" |
|
|
|
|
"-" |
|
|
|
|
|
|
Total |
|
|
|
Un astfel de tabel este de natura sa ne puna la dispozitie posibilitatea de a aprecia daca exista sau nu o dependenta între prezenta retinopatiei si a nefropatiei, adica daca cei doi factori au sau nu tendinta de a aparea în tandem. Din inspectia datelor din tabel se poate observa mai greu daca avem o astfel de tendinta de aparitie împreuna a celor doi factori. Pentru a întelege mai bine cum se pune problema acestei dependente între factori sa mai consideram si urmatoarele situatii
Tabelul 3.2. Clasificarea a 74 de subiecti dupa criteriul prezentei sau absentei bolii si dupa criteriul consumului de cartofi (Cazul Oswego, tabelul TOP)
|
|
|
Potato (Cartofi) |
||
|
|
|
DA |
NU |
Total |
|
Bolnavi |
DA |
|
|
|
|
NU |
|
|
|
|
|
Total |
|
|
|
|
Este vorba despre un eveniment petrecut în urma cu mai multi ani în America, si anume, dupa ce au luat masa la o cantina, dintr-un numar de 75 de indivizi, foarte multi s-au prezentat la medic prezentând simptomele clare ale unei intoxicatii acute. Indivizii consumasera alimentele dintr-un meniu multiplu, ceea ce facuse ca fiecare aliment sa fie consumat doar de o parte a lor, din cei 75 îmbolnavindu-se 46.
Era natural sa se încerce sa se centralizeze ce alimente a consumat fiecare individ si sa se încerce sa se stabileasca o dependenta între consumul unui anumit aliment si îmbolnaviri. În tabelul 3.2, este redata situatia referitoare la consumul de piuré de cartofi, iar în tabelele 3.3 si 3.4 situatia referitoare la consumul de sunca si înghetata de vanilie, doua alte feluri de mâncare servite în acea seara.
Aceste tabele sunt foarte utile în medicina deoarece, în ciuda informatiei sarace pe care o contin, (doar patru numere, în esenta, cele patru numere din casutele evidentiate cu text îngrosat în fiecare dintre tabele), posibilitatile de a aprecia o dependenta între clasificarile pe orizontala si verticala sunt destul de bine studiate în acest moment.
În cele doua tabele de mai sus, factorii de clasificare sunt Retinopatie, Nefropatie si respectiv, Bolnavi si Cartofi. Retinopatie, este aici criteriu de clasificare în sensul ca pacientii sunt împartiti dupa acest criteriu în doua: cei care au retinopatie si cei care nu au retinopatie. Acest lucru, poate fi simbolizat prin DA si prin NU, iar în cazul din tabel cu "+" si "-". Îl numim criteriu orizontal spre deosebire de Nefropatie care este numit criteriu vertical, pentru usurinta expunerii. La fel, în al doilea tabel, Bolnavi si Cartofi, simbolizeaza faptul ca indivizii cuprinsi în tabel sunt sau nu sunt bolnavi si respectic au consumat sau nu au consumat cartofi.
Sa încercam acum sa verificam în ce masura factorii de clasificare de pe orizontala si de pe verticala depind unul de altul în cazurile tabelelor 3.1 - 3.4.
La tabelul TOP, (factorii de pe orizontala si verticala sunt îmbolnavirile si consumul de cartofi) întâmplarea a facut ca exact jumatate din cei înregistrati au consumat mâncare de cartofi iar între cei bolnavi si sanatosi tot jumatate au consumat acest fel de mâncare. La o examinare sumara a tabelului se poate deduce imediat ca nu acest fel de mâncare este vinovat de infestarea indivizilor bolnavi, fiind evident ca jumatate din cei bolnavi nu au consumat acest fel si deci este clar ca s-au îmbolnavit de la altceva. Pe de alta parte, se vede ca si 14 indivizi care au mâncat din acest fel de mâncare nu s-au îmbolnavit. Concluzie: consumul de cartofi si îmbolnavirile nu sunt dependente.
Tabelul 3.3. Clasificarea a 75 de subiecti dupa criteriul prezentei sau absentei bolii si dupa criteriul consumului de sunca (Cazul Oswego, tabelul TOB)
|
|
|
Bakedham (sunca) |
||
|
|
|
DA |
NU |
Total |
|
Bolnavi |
DA |
|
|
|
|
NU |
|
|
|
|
|
Total |
|
|
|
|
În tabelul TOB, aparent lucrurile stau diferit, desi se observa din nou o împartire interesanta, adica din cei 75 de indivizi, raportul celor care au consumat sunca fata de cei care nu au consumat este de 46 la 29, adica exact raportul celor care s-au îmbolnavit fata de cei sanatosi, adica tot 46 la 29. Nu înseamna ca acesta ar fi alimentul vinovat, caci se vede ca sunt 17 indivizi care au consumat acest aliment dar nu s-au îmbolnavit si înca 17 care nu au consumat si totusi s-au îmbolnavit. De fapt, din cei care au consumat raportul bolnavi/sanatosi este de 29/17=1,7 iar din cei care nu au consumat raportul este 17/12=1,42 ceea ce arata ca aproximativ aceeasi proportie s-au îmbolnavit printre ambele categorii, deci, nu avem tendinta de dependenta. Concluzie: consumul de sunca si îmbolnavirile nu sunt dependente.
Tabelul 3.4. Clasificarea a 75 de subiecti dupa criteriul prezentei sau absentei bolii si dupa criteriul consumului de înghetata de vanilie (Cazul Oswego, tabelul TOV)
|
|
|
Vanilla (Inghetata de Vanilie) |
||
|
|
|
DA |
NU |
Total |
|
Bolnavi |
DA |
|
|
|
|
NU |
|
|
|
|
|
Total |
|
|
|
|
În schimb, tabelul TOV, prezinta o situatie total diferita, caci se observa ca din cei 46 de bolnavi 43 au consumat înghetata de vanilie iar marea majoritate a celor care sunt sanatosi nu au consumat. Mai putem privi situatia si astfel: din 54 indivizi care au consumat înghetata, 43 s-au îmbolnavit, iar din cei 21 care nu au consumat, 18 nu s-au îmbolnavit.
Altfel spus,
Este destul de clar ca între consumul de înghetata de vanilie si îmbolnaviri este o dependenta.
Am ales aceste exemple tocmai pentru faptul ca se vede fara dificultate care este situatia si în acest fel ne va fi mai usoara întelegerea principiilor care stau la baza aprecierii acestui tip de dependente. Din examinarea exemplelor de mai sus se vede ca în fond se poate judeca fiecare situatie care apare într-un mod asemanator, judecând de la caz la caz daca exista sau nu o dependenta între criteriile de clasificare pe orizontala si pe verticala.
Daca am judeca mereu ca mai sus am fi pusi des în situatia de a nu putea lua o decizie suficient de obiectiva. Daca de exemplu, la cei care au consumat alimentul proportia îmbolnavirilor este 79,6% (vezi tabelul 3.4), iar la ceilalti este doar de 14,2%, oricine va spune ca îmbolnavirile sunt într-o relatie de dependenta cu alimentul consumat, iar daca procentele ar fi, 79,6% si respectiv 77,4%, oricine ar spune ca mica diferenta se datoreaza întâmplarii si nu este nici o dependenta între îmbolnaviri si consumul alimentului.
Dar daca cele doua procente sunt 79,6% si 62,4% ce concluzie tragem? Caci daca am spune ca avem o dependenta din cauza diferentei de procente, oricine poate replica ca aceasta diferenta este întâmplatoare, mai ales daca numarul de pacienti pe care l-am luat în calcul a fost mic. De aceea este nevoie de criterii mai obiective de apreciere a situatiilor cu care ne putem confrunta în astfel de studii.
Trebuie retinut din cele discutate:
Poz+ numarul indivizilor asupra carora actioneaza factorul activ si rezultatul este pozitiv,
Aceasta situatie se poate centraliza într-un tabel ca tabelul 3.5, care este foarte asemanator cu cele care au fost date ca exemplu mai sus:
Tabelul 3.5. Tabel general de incidenta 2x2 (TG)
|
|
|
Factor Activ (Cauza) |
||
|
|
|
Pozitiv |
Negativ |
Total |
|
Factor Pasiv (Efect) |
Pozitiv |
Poz+ (a) |
Poz-(b) |
Poz |
|
Negativ |
Neg+ (c) |
Neg- (d) |
Neg |
|
|
Total |
|
|
N |
|
Sa încercam sa sistematizam observatii mai generale care sa ne ofere, pe cât posibil criterii mai obiective:
Daca factorul pasiv are tendinta de a apare în tandem cu cel activ, atunci ne putem astepta, ca tendinta generala, ca cei mai multi indivizi sa apara înscrisi în celulele Poz+ si Neg-, iar celulele Poz- si Neg+ sa ramâna mai nepopulate. Este de uz comun etichetarea celulelor cu a, b, c, d, ca în tabelul TG si deci vom spune ca în acest caz, majoritatea indivizilor sunt în celulele a, d, iar în celulele b, c avem mai putini indivizi (este cazul tabelului TOV). Ţinând cont de aceasta observatie, vom introduce câteva criterii de dependenta care ne permit o apreciere mai obiectiva a unei eventuale dependente.
3.2 Criterii de dependenta
O modalitate de a aprecia tendinta celor doi factori de a apare în tandem adica tendinta lor de dependenta, este de a urmari care este raportul dintre numarul pacientilor la care avem potrivire, adica ambii factori sunt prezenti sau ambii sunt absenti, si numarul pacientilor la care nu avem potrivire, adica un factor este prezent iar celalalt absent. Se observa usor ca acest raport este:
În tabelul TOV, avem CD = (43+18)/(3+11) = 61/14 = 4,35, adica sunt de 4,35 ori mai multi pacienti la care cei doi factori apar în tandem decât cei la care un factor este prezent si celalalt absent. Tendinta de dependenta este clara între consumul înghetatei de vanilie si îmbolnaviri.
În tabelul TOB, avem CD = (29+12)/(17+17) = 41/34 = 1,2, adica sunt aproximativ la fel de multi pacienti la care cei doi factori apar în tandem decât cei la care un factor este prezent si celalalt absent. Tendinta de dependenta între consumul de sunca si îmbolnaviri este absenta.
Un alt criteriu este de a calcula raportul dintre numarul pacientilor la care cei doi factori apar în tandem si numarul total de pacienti, ceea ce este mai natural caci calculeaza de fapt procentul de pacienti la care apar aceste potriviri. Deci:
În tabelul TOV, avem CP = (29+12)/75 = 41/75 = 0,546, adica sunt de 54,6% potriviri, ceea ce este o majoritate care arata o tendinta clara de dependenta între consumul înghetatei de vanilie si îmbolnaviri.
În tabelul TOB, avem CP = (43+18)/75 = 61/75 = 0,813, adica sunt de 81,3% potriviri, ceea ce este o majoritate insuficienta, care arata lipsa unei tendinte clare de dependenta între consumul de sunca si îmbolnaviri.
Un indice mult folosit în aprecierea tendintei de dependenta este raportul sanselor sau cota (Engleza ODDS RATIO = OR) raportul dintre a/c si b/d, sau, ceea ce este acelasi lucru, dintre produsul a*b si produsul c*d. Daca lucrurile stau ca mai sus, OR va avea valori cu atât mai mari cu cât tendinta de dependenta este mai puternica.
Raportul sanselor are formula:
si are urmatoarea interpretare:
Tabelul 3.6. Clasificarea a 181 de pacienti dupa tipul de tratament aplicat (T1 sau T2), si dupa evolutia bolii (pozitiva sau negativa) (Tabelul TT)
|
|
|
Tratament |
|
|
|
|
|
T1 |
T2 |
Total |
|
Evolutie |
Pozitiva |
|
|
|
|
Negativa |
|
|
|
|
|
|
Total |
|
|
|
Reluând, cele cinci situatii prezentate dau urmatoarele rezultate:
Tabelul 3.7 Folosirea criteriului OR pentru aprecierea dependentei factorilor de clasificare din tabelele 3.1, 3.2, 3.3, 3.4, 3.6
|
Tabelul |
OR |
Dependenta |
|
TRN |
|
DA |
|
TOP |
|
NU |
|
TOB |
|
NU |
|
TOV |
|
DA |
|
T1T2 |
|
DA |
Este de retinut ca nu totdeauna dependentele descoperite astfel sunt cauzale. Astfel, în exemplele TOP, TOB, TOV, T1T2, dependentele sunt cauzale în sensul ca alimentul consumat sau tratamentul poate fi considerat cauza, iar aparitia bolii sau ameliorarea ei este efectul. Totusi, în exemplul TRN, factorii nefropatie si retinopatie desi sunt într-o relatie de dependenta, nu mai sunt neaparat cauza si efect ci mai curând amândoua sunt induse de o cauza comuna. anume prezenta diabetului.
Interpretarea în limbaj uzual a acestor dependente trebuie facuta de la caz la caz si anume, pentru exemplele de mai sus putem spune:
Alt indice al unei eventuale dependente mult utilizat este riscul relativ (RR. Engl: Relative Risk), care are formula:
Indicele RR este interpretat de obicei asemanator cu OR si el indica aceeasi tendinta de dependenta daca are valori mult îndepartate de 1 (mult mai mari sau mult mai mici).
Tabelul 3.8 Folosirea criteriului OR pentru aprecierea dependentei factorilor de clasificare din tabelele 3.1, 3.2, 3.3, 3.4, 3.6
|
Tabelul |
RR |
Dependenta |
|
TRN |
|
DA |
|
TOP |
|
NU |
|
TOB |
|
NU |
|
TOV |
|
DA |
|
T1T2 |
|
DA |
Riscul relativ are si un avantaj mai putin pus în evidenta pâna acum. Anume, ce se întâmpla în exemplul TT daca tratamentul T1 este atât de eficace încât toti pacientii tratati evolueaza pozitiv. În acest caz, tabelul TT va arata ca în tabelul 3.9:
Tabelul 3.9. Clasificarea a 181 de pacienti dupa tipul de tratament aplicat, si dupa evolutia bolii, cazul când T1 ar fi un tratament perfect (Tabelul TPT)
|
|
|
Evolutie |
|
|
|
|
|
Pozitiva |
Negativa |
Total |
|
Tratament |
T1 |
|
|
|
|
T2 |
|
|
|
|
|
|
Total |
|
|
|
Se observa ca OR nu poate fi calculat în acest caz (OR = (77*18) / (0*86)), imposibil.). În schimb RR = ((77*104) / (86*77)) = 1,209, ceea ce ne arata ca exista o usoara tendinta de dependenta a evolutiei în raport cu tratamentul.
Folosirea riscului relativ în aprecierea relatiilor de dependenta trebuie facuta totusi cu precautie caci el are unele proprietati ce sunt strâns legate de studiile de epidemiologie si îl fac uneori greu de interpreta în alte contexte decât cele legate de epidemiologie. Anume, riscul relativ este un indice al tendintei de legatura într-o populatie între un factor de risc la care populatia sau o parte a ei este supusa si o afectiune care este banuita sau despre care se stie ca ar provocata sau influentata chiar de factorul de risc respectiv.
De exemplu, un factor de risc pentru maladiile cardiovasculare este stressul. De aceea, este util sa se studieze legatura între acest factor de risc si o boala cariovasculara cum ar fi hipertensiunea. În acest caz, tabelul de incidenta trebuie sa arate ca tabelul 3.10
Tabelul 3.10. Clasificarea a 4500 de indivizii dupa prezenta stressului si faptul de a fi sau nu hipertensivi
|
|
|
Stress |
|
|
|
|
|
DA |
NU |
Total |
|
HTA |
DA |
|
|
|
|
NU |
|
|
|
|
|
|
Total |
|
|
|
Riscul relativ are un înteles apropiat de cel dat initial de statisticieni, în acest context sau în contexte asemanatoare.
Riscul relativ este raportul dintre riscul de a fi afectati între cei supusi unui factor de risc si riscul de a fi afectati între cei care nu sunt supusi la factorul de risc.
Din exemplu de mai sus, se observa ca între cei supusi la stress, riscul de a avea HTA este 236/720 = 32,7%. Pe de alta parte, la cei neexpusi, riscul este de 148/3396, adica 4,35%. Raportul între cele doua riscuri, sau riscul relativ este 32,7/4,35 = 7,51. Acesta este un risc relativ foarte mare. El exprima în esenta faptul ca prezenta HTA la cei expusi este de aproximativ sapte ori si jumatate mai probabila decât la cei neexpusi.
3.3 Alte tabele de incidenta
Tabelele de incidenta nu sunt neaparat tabele 2x2 caci unul sau altul sau ambele criterii dupa care se realizeaza clasificarea pot avea mai mult de doua categorii. De exemplu, daca unul din criterii este stadiul evolutiv al unei afectiuni maligne, iar celalalt este raspunsul terapeutic, fiecare din cele doua criterii de clasificare are în mod normal, mai mult de doua categorii în care trebuie clasificati pacientii.
Stadiul evolutiv ar avea cel putin patru categorii (stadiul I, II, III si IV), iar raspunsul terapeutic ar putea avea categoriile RC (remisiune completa), RP (remisiune partiala), RN (raspuns negativ) si D (disparut). Un exemplu este furnizat de tabelul 3.10, care are 16 celule, corespunzator la 4x4 categorii (celulele cu totaluri depind de celelalte si ele nu sunt considerate în tabelele statistice ca aducatoare de informatie noua).
Tabelul 3.10. Cazul în care cele doua criterii de clasificare
au mai mult de doua categorii.
|
|
|
RASPUNS TERAPEUTIC |
|
|||
|
|
|
RC |
RP |
RN |
D |
Total |
|
STADIU EVOLUTIV |
I |
|
|
|
|
|
|
II |
|
|
|
|
|
|
|
III |
|
|
|
|
|
|
|
IV |
|
|
|
|
|
|
|
|
Total |
|
|
|
|
|
Tabelele de dimensiuni mai mari decât 2x2, sunt mult mai greu de studiat, metodele de studiu fiind mult mai putin puse la punct.
|
|
|
|
|
|
|
|
|
peste 50 |
|
sub 15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3.4 Teste clinice si aprecierea calitatii lor
Alte cazuri în care este utila folosirea tabelelor 2x2, sunt cele în care se evalueaza calitatea unui test clinic la care pacientii sunt supusi. Un astfel de test trebuie sa ofere posibilitatea de a alege pacientii care prezinta sau nu o afectiune, un simptom, un semn sau alta caracteristica necesara în procesul diagnosticarii. Vom numi pozitivi, pacientii care în urma testului au un rezultat pozitiv, care indica prezenta afectiunii, indiferent daca în realitate afectiunea este sau nu prezenta la pacientul respectiv. Vom numi negativi, pacientii care în urma testului au un rezultat negativ, indiferent daca în realitate au sau nu prezenta afectiunea respectiva.
Un test care se aplica pacientilor este o metoda care trebuie sa aiba mai multe calitati, între care, vom enumera câteva:
Ideal ar fi ca toti pacientii sa fie diagnosticati de test corect, dar acesta este un deziderat care este foarte greu de atins chiar cu aparatura perfectionata. Totdeauna exista cazuri care sunt extrem de greu de încadrat sigur într-o categorie sau alta. Asadar, totdeauna, în urma aplicarii unui test la mai multi pacienti, se vor întâlni cazuri de pacienti care, fie în realitate sunt pozitivi, iar în urma testului sunt negativi, fie invers.
Pacientii diagnosticati cu un test clinic se împart dupa doua criterii:
Deci, fiecare din pacienti, va apartine uneia din urmatoarele patru clase, care rezulta în urma combinarii în toate modurile posibile a celor patru categorii de mai sus:
Dupa ce se stabileste la fiecare pacient carei clase apartine, din cele patru enumerate mai sus, se realizeaza un tabel 2x2 ca în tabelul 3.11.
Tabelul 3.11. Clasificarea unor subiecti dupa faptul ca sunt sau ca nu sunt bolnavi (testul sigur) si dupa rezultatul pe care îl obtin la un test de diagnosticare pe care dorim sa îl evaluam calitativ. (Tabelul TGT)
|
|
|
Testul sigur |
|
|
|
|
|
Bolnavi |
Sanatosi |
Total |
|
Testul propus |
Pozitivi |
Real Pozitivi (RP sau B+) |
Fals Pozitivi (FP sau S+) |
P |
|
Negativi |
Fals Negativi (FN sau B-) |
Real Negativi (RN sau S-) |
N |
|
|
|
Total |
B |
S |
B+S=P+N |
Aprecierea calitatii unui test propus trebuie evident sa tina seama de procentul de reusite ale acestuia. Dar ce înseamna reusite pentru un test clinic Câteva propuneri ar fi:
Vom defini aceste rapoarte procentuale si vom studia modul cum le folosim în aprecierea calitatii testului. Aceste procente arata calitatea unui test clinic în sensul ca testul este cu atât mai valoros cu cât ele au valori mai mari, mai apropiate de 100%. În plus, vor fi definite mai jos si doua rapoarte procentuale care exprima erorile unui test. Este clar ca procentele care exprima erorile trebuie sa fie cât mai mici pentru ca testul sa fie valoros.
Tabelul 3.12. Clasificarea a 109 femei dupa tipul de nastere (prematura sau normala) si dupa lungimea colului uterin ca test de decizie a riscului de nastere prematura. Se observa ca din 41 de nasteri premature, 33 au colul sub 26mm iar din 68 de nasteri normale, 53 au colul peste 26, deci limita de 26mm a lungimii colului uterin este un criteriu de decizie al riscului de nastere prematura.
|
|
|
Nastere |
|
|
|
|
|
Prematura |
Normala |
Total |
|
Lungime col |
<26 mm |
|
|
|
|
>26mm |
|
|
|
|
|
|
Total |
|
|
|
În tabelul 3.12, valorile indicatorilor de mai sus sunt:
Sp=53/68=0,779=77,9%
VPP=33/48=0,687=68,7%
VPN=53/61=0,868=86,8%
RFP=15/68=0,221=22,1%
RFN=8/41=0,196=19,6%
Dupa cum s-a precizat mai sus, un test este cu atât mai valoros cu cât primii patru din cei sase indicatori sunt mai mari, iar ultimii doi mai mici. În practica, se constata ca este foarte greu sa se atinga valori foarte mari pentru toti cei patru si valori foarte mici pentru ultimii doi. De exemplu, testul studiat prin tabelul 3.12 este un test valoros.
Doar primii doi indicatori sunt considerati fundamentali, ei fiind cei care dau de fapt calitatea testului clinic propus, în comparatie cu testul considerat sigur (testul de aur), în cazul de mai sus testul sigur fiind nasterea propriu-zisa.
De fapt, cunoasterea indicatorilor Sn si Sp, împreuna cu numarul pacientilor bolnavi si numarul pacientilor sanatosi, este suficient pentru a cunoaste ceilalti indicatori. Rata erorilor, de ambele tipuri, RFP si RFN sunt legate direct de Sn si Sp prin formulele:
Ceilalti doi indicatori pot fi si ei obtinuti din Sn si Sp, daca se cunosc B si S, numarul pacientilor bolnavi, respectiv sanatosi. Formulele sunt:
pe clase din 5Kg în 5Kg
|
Clasa |
Greutate(Kg) |
Frecventa (Nr indivizi) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Acum sa privim graficul din figura 5.1, care reprezinta situatia din tabel:
Figura 5.1 Histograma greutatilor corporale a 1014 pacienti cu diferite afectiuni
Mai întâi, ce s-a reprezentat de fapt Se oserva ca pe orizontala sunt figurate clasele din tabel în ordine, fiecareia fiindu-i alocat un segment egal, iar pe verticala, dreptunghiurile au înaltimi proportionale cu frecventele absolute ale claselor. Multimea barelor verticale este cea care ne da impresia vizuala pe care trebuie sa o interpretam în sensul sitetizarii informatiei. Observam:
Din stânga se începe cu bare scunde care cresc în înaltime pe masura ce ne apropiem de clasa din centru, dupa care are loc un proces invers. Este tendinta naturala la cele mai multe situatii. Datele au de cele mai multe ori tendinta de a se situa în stânga si drepta mediei, din ce în ce mai putine pe masura ce ne departam de medie. Pe acest grafic nu este figurata media dar este de bun simt sa ne gândim ca este situata undeva în clasele de mijloc.
Indivizii care au sub 35 Kg si cei peste 100 Kg, probabil foarte putini, nu au fost luati în calcul. Se obisnuieste totusi ca ei sa fie luati în considerare prin introducerea a doua clase speciale. În acest caz, clasele speciale de introdus ar fi fost: clasa sub 35 si clasa peste 100 . De obicei asa este bine sa se procedeze.
Modul cum cresc barele este diferit de modul cum descresc. Aceasta este ceea ce numeam la indicatori statistici asimetria. Aceasta histograma arata o usoara asimetrie la dreapta. Daca indivizii de la care s-au cules datele ar fi fost normali, histograma ar fi avut un aspect mai simetric. Asimetria acestei hitograme ne arata ca în clasele de la 40 la 65 Kg sunt mai multi indivizi decât în clasele simetrice lor de la 75 la 90. Având în vedere ca majoritatea lor sunt barbati, acesta asimetrie ne spune ca un numar de indivizi au gruetatea mai mica decât ar fi normal. Acest lucru este explicabil în acest caz, deoarece cei mai multi au afectiuni hepatice grave ca ciroza hepatica, cancer hepatic, si sunt într-o stare fizica mult slabita. În acest caz, am explicat forma histogramei pe baza realitatii. De obicei însa se întâmpla exact pe dos. Histograma este aceea care ne ajuta sa întelegem mai bine realitatea.
Pentru a realiza diferenta dintre o distributie simetrica si una asimetrica, sa transpunem într-o histograma situatia din tabelul 5.2, care sistematizeaza situatia supravietuirilor în cazurile de cancer mamar pe un lot de 2456 de pacienti.
Tabelul 5.2 Situatia supravietuirilor în cazurile de cancer mamar pe un lot de 2456 de pacienti. Gruparea în clase de 12 luni
|
Nr.Crt |
Perioada |
Nr.cazuri |
Procent |
Procent Cumulat % |
|
|
0..12 luni |
|
|
|
|
|
12..24 luni |
|
|
|
|
|
24..36 luni |
|
|
|
|
|
36..48 luni |
|
|
|
|
|
48..60 luni |
|
|
|
|
|
60..72 luni |
|
|
|
|
|
72..84 luni |
|
|
|
|
|
84..96 luni |
|
|
|
|
|
96..108 luni |
|
|
|
|
|
108..120 luni |
|
|
|
|
|
Peste 120 luni |
|
|
|
În figura 5.2, este reprezentata histograma corespunzatoare pentru tabelul 5.2. Se observa ca barele histogramei au înaltimi descrescatoare întocmai ca si frecventele absolute ale claselor.
Figura 5.2 Histograma corespunzatoare pentru tabelul 5.2. Se observa ca barele histogramei au înaltimi descrescatoare întocmai ca si frecventele absolute ale claselor
Se observa la aceasta histograma ca are o asimetrie foarte puternica spre dreapta. Vom considera totdeauna (ca o conventie), sa spunem ca o histograma arata asimetria spre partea unde descresterea este mai lenta. Tendinta observata în aceasta histograma este normala, având în vedere fenomenul surprins. Procesele de supravietuire sunt de obicei marcate de o distributie a valorilor cu excentricitate spre dreapta, adica spre supravietuiri lungi.
5.3 Poligonul frecventelor
Este un grafic care reprezinta frecventele absolute dintr-un tabel de frecventa printr-o linie frânta. Clasele se realizeaza ca si la histograma. Linia frânta, leaga puncte din plan care au ca ordonate frecventele de reprezentat, iar ca abscise, mijloacele claselor. Graficul se poate realiza si din histograma, prin unirea mijloacelor laturilor superioare ale barelor.
În figura 5.10 este reprezentat un exemplu de modul cum se obtine poligonul frecventelor din histograma.
Figura 5.10 Poligonul frecventelor obtinut prin unirea mijloacelor laturilor superioare ale barelor unei histograme(stânga). Poligonul frecventelor pentru greutatea a 1042 de pacienti cu diferite afectiuni, cu clase din 5 în 5 Kg(dreapta).
În figura 5.10 este reprezentat poligonul frecventelor pentru greutatea a 1042 de pacienti cu diferite afectiuni, din 5 în 5 Kg.
Desi ofera o imagine vizuala foarte buna a modului cum sunt distribuite valorile din serie pe clase, poligonul frecventelor este mai putin folosit decât histograma, care ofera si ea tot informatia despre distributia valorilor din serie pe clase. Aceasta deoarece histograma pare ochiului un grafic mai bogat. În realitate, între cele doua grafice, nu exista o diferenta calitativa. Ele ofera aceeasi informatie.
ATENŢIE! Graficul histograma si graficul poligonul frecventelor, contin exact aceeasi cantitate de informatie, daca au la baza acelasi tabel de frecvente.
5.4 Graficul cu bare
Este graficul care reprezinta prin bare verticale, frecventele unui tabel de frecvente pentru variabile calitative (date nominale) sau variabile ordinale. Desi pare asemanator cu histograma, între cele doua tipuri de grafice exista diferente. Ca aspect, histograma are barele lipite în timp ce graficul cu bare lasa o oarecare distanta între bare. Nu este recomandata folosirea graficelor unul în locul celuilalt.
În figura 5.12 sunt reprezentate frecventele de aparitie a unor afectiuni maligne, pe stadii.
Figura 5.12 Clasificarea pe stadii a unui numar de pacienti cu afectiuni maligne
Tabelul 5.1 frecventele deceselor în timpul operatiei într-o sectie de spital
|
Anul |
Nr. Cazuri |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Figura 5.13 Graficul histograma si graficul cu bare, cu datele din tabelul 5.1
Graficul Scatter (Graficul punctual, Graficul de corelatie)
Este un grafic care:
Acest grafic este extrem de util în statistica, furnizând o informatie bogata, deoarece nu pierde din informatie ca histograma. Pentru explicatii privind informatia furnizata de acest grafic, vezi capitolul 9. În figurile 5.22 - 5.27 sunt redate câteva grafice de acest tip întâlnite în practica.
Figura 5.22 Graficul de corelatie între greutatea si înaltimea a 1042 de pacienti cu diferite afectiuni
Figura 5.23 Graficul de corelatie între tensiunea sistolica si diastolica a 593 de pacienti cu diferite afectiuni
Figura 5.24 Graficul de corelatie între bilirubinatotala si bilirubina conjugata la 521 de pacienti cu diferite afectiuni
Figura 5.25 Graficul de corelatie între viteza de sedimentare a hematiilor la o ora si la doua ore la 292 de pacienti cu diferite afectiuni
6. Repartitii
6.1 Curba densitatii de probabilitate
S-a vazut ca histograma este un grafic care da informatii despre repartizarea valorilor dintr-o serie de valori, care arata daca valorile din serie sunt repartizate simetric sau asimetric si daca repartitia are un singur vârf sau este multimodala.
Sa ne imaginam ca pe masura ce marim indefinit numarul de valori din serie, lungimea claselor scade foarte mult, astfel încât obtinem histograme din ce în ce mai "fine". Ce se obtine prin acest proces? O apropiere din ce în ce mai accentuata de repartitia reala a datelor, repartitie pe care histogramele o aproximeaza din ce în ce mai bine.
Histogramele ofera imaginea repartizarii valorilor dintr-o serie, deci o imagine incompleta a realitatii. Într-adevar, valorile dintr-o serie de date sunt culese pe un esantion sau lot, care este de obicei extras dintr-o populatie mult mai numeroasa. Ceea ce ne intereseaza de obicei însa, este modul cum se repartizeaza valorile din întreaga populatie.
În figura 6.1, este dat un exemplu de serie de valori foarte mare, alcatuita din 10000 de valori. În acest caz, lotul pe care s-au facut masuratorile poate fi numit populatie, numarul de indivizi fiind foarte mare.
Figura 6.1 Folosind o serie de 10000 de valori, se pot face histograme din ce în ce mai fine, care trec de la aspectul de ″treapta″, la acela de ″curba″
Pe masura ce histogramele devin din ce în ce mai fine, ele tind sa se asemene cu o curba. Daca volumul seriei ar fi mult mai mare, asemanarea cu o curba ar fi atât de clara încât ochiul nu ar mai putea observa aspectul de ″treapta″.
Strict vorbind, notiunea de curba densitatii de probabilitate, trebuie introdusa folosind un aparat teoretic mai complex. Deoarece o introducere fundamentata ar depasi nivelul cartii de fata, vom considera, intuitiv, fara a pretinde ca aceasta este o definitie ca:
Figura 6.3 Diverse forme ale curbei densitatii de probabilitate
Pe masura ce statistica a evoluat ca stiinta, s-a demonstrat ca unele din curbele densitatii de probabilitate joaca un rol central în stiinta în general si în medicina în special. Astfel, multe fenomene din stiinta se petrec astfel încât deviatiile stânga-dreapta de la medie ale masuratorilor pe care le facem sunt repartizate simetric si nu oricum, ci tind sa fie repartizate foarte asemanator cu o anumita curba, mult studiata, care se numeste curba densitatii normale sau curba Gauss.
Astfel, asa cum se va vedea în capitolul despre esantionare, media de esantionare, adica media calculata asa cum a fost descris în capitolul 2, are în anumite conditii o repartitie normala. În subcapitolele care urmeaza vor fi descrise câteva din curbele de repartitie mai folosite si mai des întâlnite în practica.
Curbele de repartitie se bucura de câteva proprietati care le fac extrem de utile în statistica, asa cum se va vedea în capitolele despre esantionare si despre testele statistice.
Figura 6.4 Aria cuprinsa între o curba de repartitie si axa orizontala
este totdeauna 1 sau 100%
Figura 6.5 Daca extragem aleator un individ dintr-o populatie care are curba de repartitie cunoscuta, valoarea masurata la acel individ este cuprinsa între doua numere reale a si b cu o probabilitate egala cu aria cuprinsa între curba, axa orizontala si cele doua verticale în a si b.
6.2 Densitatea Normala
Curba Gauss, sau clopotul lui Gauss a jucat în istoria stintei si joaca si acum un rol foarte important, iar în medicina foarte multi parametri legati de organismul uman, de legile fundamentale ale viului, sunt repartizati dupa aceasta curba. Ce este de fapt aceasta curba?
Formula curbei lui Gauss, este:
Se observa ca aceasta curba depinde de doi parametri, m si s, si ea este perfect determinata în momentul în care se cunosc acesti parametri. Deoarece curba descrie repartitia unei populatii, cei doi parametri reprezinta media (m) si abaterea standard (s) ale populatiei respective.
Graficul din figura 6.6, care este graficul unei curbe Gauss, ne arata ca, spre centru probabilitatile sunt cu atât mai mari cu cât suntem mai aproape de medie, iar spre margini probabilitatile scad apropiindu-se de zero pe masura ce ne îndepartam din ce în ce mai mult de medie. Curba este simetrica, niciodata însa simetria nu este perfecta pe o histograma particulara sau pe un poligon al freceventelor, dar curba ideala este perfect simetrica. Subliniem ca prin curba ideala întelegem curba catre care se îndreapta poligonul frecventelor când numarul de cazuri tinde la infinit iar lungimea claselor se apropie de zero. Uneori, graficul functiei este denumit "clopotul lui Gauss" datorita formei lui deosebite, asemanatoare unui clopot.
Figura 6.6 Curba repartitiei normale, sau curba lui Gauss. Are un maxim în dreptul mediei, doua puncte de inflexiune (în dreptul valorilor m-s si m+s), tinde la zero pe masura ce ne îndepartam de medie la stânga si la dreapta
În analiza matematica se arata ca graficul acestei functii, cel din figura 6.6, are un maxim pentru x=m si doua puncte de inflexiune (în care devine din concava convexa), la m-s si la m+s.
Curba normala mai este cunoscuta sub denumirea de legea Gauss-Laplace sau legea normala si apare pentru prima data într-o lucrare a matematicianului Moivre (1667 - 1754), apoi în lucrarile lui Pierre Simon de Laplace (1749 - 1827). Celebra este facuta de lucrarile matematicianului Gauss (1777 - 1855). Utilitatea acestei repartitii se datoreaza mai multor cauze, printre care:
Trebuie retinut ca repartitia Gauss are urmatoarele proprietati importante:
Figura 6.7 Aria cuprinsa între curba, axa orizontala si doua verticale în dreptul numerelor a si b, este probabilitatea ca, extragând aleator un individ din populatie si facând masuratoarea pe acel individ, valoarea obtinuta x, sa fie între a si b
Repartitia Gauss, este de fapt o famile de repartitii ce depinde cei doi parametri: media si deviatia standard. În figura 6.8, sunt desenate câteva curbe de repartitie Gauss, mai mult sau mai putin aplatizate, dupa cum deviatia standard este mai mica sau mai mare.
Figura 6.8 Diferite curbe Gauss mai mult sau mai putin aplatizate, aplatizarea fiind data de valoarea deviatiei standard, s. Cu cât valoarea lui s este mai mare, cu atât curba este mai aplatizata. Când s ia valori mici, curba este mai înalta.
Avem de asemenea, o infinitate de curbe Gauss care au aceeasi deviatie standard dar au medii diferite. Ele sunt identice ca forma, doar sunt localizate diferit în plan si pot fi suprapuse prin translatii stânga-dreapta. În figura 6.9, sunt desenate câteva curbe Gauss care difera numai prin medie. Având toate aceeasi deviatie standard, au aceeasi aplatizare.
Figura 6.9 Curbe Gauss cu aceeasi deviatie standard. Ele sunt la fel de aplatizate si pot fi suprapuse prin translatii stânga-dreapta.
Daca fixam media dar permitem orice deviatie standard, exista o infinitate de curbe Gauss care au aceeasi medie. Ele sunt localizate identic stânga-dreapta, dar difera prin aplatizare mai mult sau mai putin accentuata. În figura 6.10, sunt desenate 3 curbe Gauss cu aceeasi medie si cu deviatiile standard 1, 1.2 si 1.5.
Figura 6.10 Trei curbe Gauss cu aceeasi medie si deviatii standard diferite
Un caz special de curba Gauss se obtine daca m=0 si s=1, caz în care functia f are forma:
expresie care are graficul în figura 6.11. Pentru x=0, valoarea functiei este aproximativ 0,4, deoarece e0=1. Valorile lui f scad foarte repede odata cu cresterea lui x, fie în sensul pozitiv, fie în sensul negativ. Aceasta deoarece expresia lui f se mai scrie ca:
Dupa cum se stie, exponentiala este una din functiile care cresc extrem de rapid (crestere exponentiala), ceea ce face ca f(x) sa scada extrem de repede cu cresterea lui x. De exemplu, daca x = 3, sau x = -3, atunci f(x)=0,004, aproximativ. Pentru valori ale lui x mai mari decât 3 sau mai mici decât -3, valoarea lui f este neglijabil de mica (vezi subcapitolul 6.3 pentru amanunte privind aceasta repartitie speciala).
Figura6.11 Curba lui Gauss corespunzatoare la m=0 si s=1. Are un maxim egal cu aproximativ 0,4. Se observa ca scade extrem de repede odata cu îndepartarea de 0. Valorile ei dincolo de 3 si de -3 sunt neglijabil de mici. Se mai numeste curba Gauss standard
Asa cum am aratat, repartitia normala sau Gaussiana este des întâlnita în studiul fenomenelor biologice si are unele proprietati utile. În biologie, una din problemele importante care se pun în legatura cu datele pe care le masuram este aceea daca se încadreaza sau nu în limitele de normalitate. Repartitia normala ne poate ajuta sa dam un raspuns acestei întrebari, cel putin pentru acele date care sunt distribuite normal. Daca o variabila are repartitie Gauss, atunci se poate stabili cât de plauzibila este media si deviatia standard gasite prin masuratori pe un lot si se pot face comparatii cu mediile care ar trebui sa fie obtinute si care sunt cunoscute din literatura de specialitate (vezi capitolul despre esantionare si cel dsepre teste statistice pentru amanunte).
Cunoscând despre o variabila ca are repartitie Gauss, se pot deduce unele afirmatii despre valorile pe care le poate lua. Cum folosim aceasta repartitie pentru a deduce anumite concluzii despre variabila care ne intereseaza? Dupa cum am mai afirmat, pentru o variabila repartizata normal, procentul din populatie situat între doua limite date este aria cuprinsa între curba Gauss, axa orizontala si cele doua verticale la limitele fixate. De obicei se considera intervalele în jurul mediei, simetrice, cu limite situate la o distanta de una sau mai multe abateri standard de medie. Astfel, se poate demonstra ca:
În intervalul m-s, m+s se afla aproximativ 68% din indivizii unei populatii repartizate normal (vezi figura 6.12). Aceasta însa nu este o majoritate suficient de mare pentru a fi aproape de siguranta daca ne întrebam între ce limite sunt situate valorile masurate pentru indivizii din populatie.
Figura 6.12 Între m-s, m+s se afla aproximativ 68% din indivizii unei
populatii repartizate normal
De aceea se ia cel mai adesea în considerare intervalul m-2s, m+2s în care se situeaza aproximativ 95% din indivizii unei populatiei repartizate normal. Acest interval este suficient de larg si cuprinde o majoritate zdrobitoare a populatiei asa ca este cel mai indicat sa fie folosit ca interval de normalitate.
Figura 6.13 Între m-2s, m+2s se afla aproximativ 95% din indivizii unei
populatii repartizate normal
Uneori, se iau intervale mai cuprinzatoare, ca m-3s, m+3s interval în care se situeaza peste 99% din populatia considerata (vezi figura 6.14).
Figura 6.14 Între m-3s, m+3s se afla peste 99% din indivizii unei
populatii repartizate normal
Chiar daca se considera de
obicei ca pentru variabilele folosite uzual în practica medicala
valorile medii sunt cunoscute si se cunosc si asa-numitele intervale de normalitate, în realitate
se cunosc doar foarte bune aproximari ale lor obtinute pe baza unor
studii foarte atente, pe loturi largi.valorile reale ale mediei si
deviatiei standard pentru o populatie distribuita normal, notate
cu m si s, sunt aproximate cu ![]() si s care
sunt indicatorii medie si abatere standard pentru un lot extras din
populatia respectiva.
si s care
sunt indicatorii medie si abatere standard pentru un lot extras din
populatia respectiva.
Cum se stabileste cât de bune sunt aceste aproximari, care se mai numesc estimari, se va vedea în capitolul 7. Oricum, se folosesc din plin proprietatile distributiei Gaussiene.
6.4 Importanta repartitiei normale
Dupa cum s-a vazut în subcapitolul 6.3, si dupa cum se va vedea si în acest subcapitol, cunoasterea unei repartitii în general este utila deoarece se pot verifica si elimina valorile aberante, se pot verifica limitele de normalitate, etc. Daca stim ca o variabila are o distributie Gauss cu media m si deviatia standard s, atunci aproximativ 99,5% din valorile acelei variabile sunt în intervalul [m-3s, m+3s]. Deci, putem considera ca într-un esantion de dimensiune destul de mare, de câteva sute de cazuri, aparitia de valori în afara acestui interval este aberanta, adica, în principiu ar trebuie eliminate. Pe de alta parte valorile pe care le consideram normale se încadreaza în asa-numitul interval de normalitate care este aproximativ [m-2s, m+2s]. Mai mult, având o valoare data, putem cere sa se verifice cât de verosimil este ca ea sa provina dintr-o populatie cu distributia Gauss, cu media m si abaterea standard s.
Pentru a întelege mai bine ideile de mai sus, sa luam un exemplu. Latenta semnalului nervos pe nervul optic la indivizii normali este în medie 105ms cu o deviatie standard de 7,5ms. Masurând latenta unui individ, se gaseste 142ms si dorim sa stabilim cât de probabil este ca o valoare peste 142ms sa provina dintr-o populatie repartizata Gauss, de indivizi normali cu media 105ms si deviatia standard 7,5ms.
În figura 6.17, sunt figurate media si valorile corespunzatoare la m-s, m+s, m-2s, m+2s, m-3s, m+3s, precum si valoarea 142ms. Desi pare ca aceasta valoare iese din grafic, în realitate curba tinde asimptotic la axa orizontala si trece pe deasupra acestei valori, chiar daca imperfectiunile desenului nu arata acest lucru. Pentru a afla cât de probabil este sa întâlnim valori de 142ms si peste, într-o repartitie Gauss cu media 105ms si abaterea standard 7,5ms, trebuie calculata aria cuprinsa între curba si orizontala, la stânga luând de la - infinit, iar la dreapta pâna la 142ms. Este clar ca aproape întreaga arie este luata, exceptând o portiune minuscula, la dreapta valorii 142ms. Aceasta portiune are o arie mai mica decât 0,000001, adica mai mica decât 0,0001%, sau 1 la 1000000. Este deci foarte improbabil ca valoarea de 142ms sa provina dintr-o populatie ca cea folosita de noi. În realitate, pacientul are scleroza multipla si provine de fapt dintr-o alta populatie, cea a pacientilor afectati de boala.
Figura 6.17 Repartitia Gauss cu media 105ms si deviatia standard 7,5ms. Valoarea 142ms este fosrte improbabil sa apartina acestei repartitii
Ne putem pune acum mai multe întrebari pentru conduita în alte situatii asemanatoare. De exemplu:
Regula celor 3 sigma. Deoarece în intervalul care se obtine prin scaderea si adunarea a trei sigma la medie este cuprinsa o arie de aproximativ 99,74% din toata aria de sub curba normala, în esantioane ce nu depasesc anumite limite de volum, în mod normal nu exista nici o valoare care sa fie în afara intervalului celor trei sigma. De aceea în general, aceste valori, atunci când totusi apar, sunt considerate aberante si sunt eliminate. Eliminarea valorilor aberante nu se face automat si fara o judectaa pentru fiecare astfel de valoare în parte. Totusi, uneori se elimina ca aberante valori care nu numai ca se afla în afara intervalului celor trei sigma, dar sunt foarte departe de marginile acestui interval. O teorema celebra, datorata lui Cebâsev spune ca, indiferent de distributie, valorile sunt practic situate între media plus-minus sase abateri standard. Deci ceea ce iese din acest interval trebuie eliminat automat ca aberant.
Regula celor 2 sigma. În mod asemanator cu regula celor trei sigma, valorile situate în intervalul obtinut prin adunarea si scaderea a doua valori ale lui sigma la m, sunt considerate ca valori normale. În acest intreval se gasesc aproximativ 95,44% din indivizii unei populatii, daca populatia are o distributie Gauss. Aceasta este considerata o majoritate suficienta pentru a lua acest interval ca interval de normalitate.
Ar rezulta ca se pot în acest fel construi intrevale de normalitate practic pentru orice tip de variabila distribuita Gauss. Din pacate, în practica lucrurile nu stau deloc asa. Intervalul de normalitate se construieste folosind media si deviatia standard ale repartitiei Gauss considerate. Dar acesti parametri sunt de obicei necunoscuti. De aceea, intervalele de normalitate puse la dispozitie de manuale si tratatele stiintifice sunt calculate pe esantioane foarte mari, astfel ca media si abaterea standard de esantionare sa aiba valori foarte apropiate de cele reale si sunt folosite în locul mediei si deviatiei standard ale întregii populatii.
Intervalele de normalitate obtinute astfel nu au valoarea stiintifica pe care le-ar avea cele care folosesc valorile exacte si nu pe cele aproximative. Totusi ele sunt singurele pe care le avem la dispozitie si nimic mai bun nu putem pretinde decât îmbunatatirea acestor intervale imprecise. De aceea se verifica în permanenta modul în care un esantion se înscrie sau nu în intervalele de normalitate citate în literatura de specialitate. De aceea sunt uneori situatii în care surse diferite dau ca intervale de normalitate valori usor schimbate, dupa autorul sau studiul care le-a obtinut. Micile diferente apar tocmai din faptul ca se folosesc valori aproximative în locul celor exacte.
Observatie: Cuvântul "normal" are în statistica alt înteles decât în limbajul curent:
6.5 Alte repartitii
6.5.2.3 Densitatea Student
Este o repartitie care intervine mult în aplicatiile referitoare la testele statistice. Are o forma simetrica si seamana ca aspect cu distributia Gauss standard.
Este în realitate o familie infinita de repartitii, pentru fiecare n, numar de grade de libertate (df), având o forma diferita.
Figura 6.27 Curbe de repartitie Student corespunzator la 3, 6 si n>120 grade de libertate. Pentru n>120, forma curbei este practic aceeasi cu cea a curbei normale standard si nu se mai schimba odata cu n.
Aceasta densitate are proprietatea ca are un maxim în 0 si este simetrica stânga-dreapta lui 0, ca forma. Are un aspect cu atât mai aplatizat cu cât numarul de grade de libertate este mai mic. Desi pare sa se asemene cu curba lui Gauss, a densitatii normale, în realitate, între ele este o diferenta.
Cînd numarul de grade de libertate tinde la infinit, aspectul ei se apropie tot mai mult de forma repartitiei Gauss.
7.1 Esantion
Indicatorii statistici calculati pentru un esantion anume sunt simple aproximari pentru parametrii reali ai populatiei din care provine esantionul. Astfel, media, sau deviatia standard calculate pentru bilirubina totala la pacientii din esantionul de 229 de ciroze si cancere hepatice, sunt aproximari ale acelorasi indicatori pentru bilirubina totala a întregii populatii de bolnavi de ciroza si cancer hepatic.
Se pune în mod natural problema de a stabili câta încredere se poate avea în aceste aproximari, sau cât de precise sunt ele. Raspunsul la o astfel de întrebare se poate da cu ajutorul testelor statistice, despre care se va discuta în capitolul urmator. Acum sa încercam sa precizam doar conditiile pe care trebuie sa le avem îndeplinite pentru ca gradul de siguranta în asertiunile pe care le facem despre o populatie pe baza rezultatelor obtinute pe un esantion, sa fie cât mai mare. Înainte de a preciza aceste conditii, sa stabilim de ce aprecierea acestei precizii de aproximare este importanta.
Deci, sa plecam de la faptul ca avem media si deviatia standard calculate pentru o anumita variabila pe un esantion anume. Daca modul în care a fost ales esantionul ne da posibilitatea sa afirmam ca acestea sunt bune aproximari ale mediei si deviatiei standard pentru întreaga populatie, atunci acesta este de fapt singurul lucru pe care ne putem baza, în afara, eventual, a unor medii sau deviatii date în literatura de specialiate.
În cazul în care nu avem astfel de date din surse bibliografice, caz destul de des întâlnit, sau când acestea nu concorda, mai rar, dar se mai întâmpla, atunci media întregii populatii nu ne va fi de fapt cunoscuta decât prin aproximarile date pe esantioane, caci, este evident ca este imposibil sa se faca masuratori pentru întreaga populatie. De fapt, sursele bibliografice nu ne dau nici ele decât tot aproximari foarte bune ale adevaratei medii sau deviatii standard, obtinute tot pe niste esantioane extrase din populatia respectiva.
Pentru o discutie ceva mai exacta, sa introducem câtiva termeni: vom numi esantion sau lot, o submultime a unei populatii statistice. Extrapolarea unor rezultate obtinute prin masuratori pe un esantion la întreaga populatie o vom numi inferenta. De exemplu, daca media bilirubinei totale pe un esantion de ciroze este 2,35, putem face afirmatia generalizatoare, sau inferenta, ca media bilirubinei la ciroze este 2,35.
Cât de îndreptatite sunt astfel de inferente vom vedea ceva mai departe, dar adevarate sau nu, în principiu se pot face orice astfel de inferente. O afirmatie despre o populatie, despre care nu stim daca este sau nu adevarata, si pe care , eventual încercam sa o verificam, o vom numi ipoteza statistica. De exemplu se poate face ipoteza ca media bilirubinei la cirozele si cancerele hepatice este 2,35 si ne propunem sa verificam acesata ipoteza în ce priveste veridicitatea ei. În cele ce urmeaza, vor fi expuse unele tehnici de inferenta care pleaca de la ideia ca esantioanele pe care se lucreaza îndeplinesc niste conditii destul de naturale, firesti, dar obligatorii întrucât toate concluziile care se trag sunt conditionate de ele. Vom enumera în continuare câteva din aceste conditii:
a) Volumul
Vom numi volum al unui esantion, numarul de indivizi din acel esantion. Evident ca masuratori efectuate pe un individ dintr-o populatie, sau pe câtiva indivizi, nu ne pot oferi o imagine veridica a rezultatelor care s-ar obtine daca s-ar putea masura întreaga populatie. Se pune întrebarea, câti indivizi trebuie masurati, astfel încât sa avem un minim de siguranta asupra rezultatelor obtinute? Raspunsul la aceasta întrebare nu exista. Nimeni nu ne poate spune acest numar, sa-i zicem, minimal de masuratori. O afirmatie care tine mai mult de un soi de folclor statistic, spune ca nu se poate face statistica cu mai putin de 30 de masuratori. În realitate acest numar depinde foarte mult de populatia asupra careia se lucreaza. O afectiune foarte raspândita ca diabetul zaharat, care da o populatie foarte numeroasa la nivelul unei tari sa zicem, de câteva zeci de mii de cazuri, nu poate fi studiata pornind de la esantioane de 30 - 40 de indivizi, ci în mod necesar, de cel putin câteva sute. Din contra, o maladie rara care abia daca strânge câteva zeci de indivizi la nivelul unei tari, pune problema gasirii la un moment dat a câtorva indivizi si nicidecum a câtorva zeci. De altfel, statistica a demonstrat ca în realitate numarul de indivizi din esantion este doar cel care da siguranta inferentei, un volum prea mic al esantionului, ducând pur si simplu la rezultate nesemnificative, asa cum se va vedea. Cu cât mai multe înregistrari, cu atât mai sigure inferentele pe care le facem.
b) Reprezentativitatea
Este conditia cruciala, care necesita discutii foarte complexe si argumente serioase, inclusiv matematice si care se poate rezuma în cerinta ca esantionul pe baza caruia se fac inferente despre populatie sa reflecte particularitatile populatiei din care provine. Astfel, în cazul unei maladii cu incidenta crescuta în rândul femeilor, cum este Lupus Eritematos Sistemis, nu se pot lua esantioane în care proportia de barbati si femei este aceiasi ci esantioane care sa aiba cam aceiasi proportie de femei si barbati ca si populatia. Acesta este un exemplu legat de repartitia pe sexe, dar în realitate, trebuie sa se tina seama de o serie de alte conditii obligatorii, legate de particulatitatile de vârsta, mediu de provenienta, rasa, uneori chiar nivel de cultura sau zona geografica si altele. Vom spune ca un esantion este reprezentativ numai în conditiile în care el reflecta la scara mica toate, sau cât de multe posibil, particularitatile populatiei din care provine.
c) Aleatorizarea sau randomizarea
Este o conditie legata de precedenta si presupune ca alegerea indivizilor din esantion trebuie facuta la întâmplare caci numai astfel pot fi eliminate unele tendinte subiective ale celui care face alegerea si care, oricât ar dori, nu se poate sustrage tuturor pericolelor de a alege indivizii din esantion dupa niste criterii pe care de cele mai multe ori nici nu le banuieste dar ele ar putea exista. Sunt cazuri speciale în care alegerea indivizilor din esantion se face dupa criterii anume dar acestea au fost verificate de-a lungul timpului si au un suport stiintific bine întemeiat. Pentru a înlatura orice suspiciune de alegere subiectiva, se prefera alegerea întâmplatoare. O mentiune speciala merita cazul în care înregistrarile provin de fapt din baze de date construite si completate în timpul actului medical la un cabinet de specialitate, într-o clinica, etc, caz în care, evident ca nu avem posibilitatea de a controla modul în care pacientii se prezinta la medic. În aceste cazuri facem observatia ca în afara unor evenimente speciale de tipul epidemiilor, campaniilor de control medical monitorizat, când pacientii nu se mai prezinta la medic la întâmplare, ci sunt mânati de o cauza ce nu tine direct de hazard, înregistrarile obisnuite produc esantioane care sunt de obicei întâmplator alese din populatiile respective.Totusi este bine sa se verifice pe cât posibil daca esantioanele înregistrate îndeplinesc celelalte conditii cerute.
d. Independenta masuratorilor
Orice calcul statistic facem cu datele pe care le avem la dispozitie presupune apriori ca ele sunt independente una de alta. În medicina aceasta cerinta este de obicei îndeplinita în mod automat si anume, atunci când datele reprezinta valorile aceluiasi parametru masurat la mai multi pacienti, deoarece valoarea obtinuta pentru pacientul nr.1 este independenta de valoarea obtiunuta pentru pacientul nr.2 si ambele sunt independente de valorile pe care le obtinem la ceilalti pacienti. Sunt însa cazuri în care un pacient care a fost internat de mai multe ori si parametrul urmarit este masurat de fiecare data, valorile obtinute nu sunt neaparat independente unele de altele.
De exemplu, daca ne intereseaza valorile legate de functia hepatica, la pacienti cu ciroza hepatica, atunci, la reinternari, masurarea unui parametru care nu este direct legat de functia hepatica nu da valori independente. Tensiunea sistolica ar putea fi chiar aceeasi la câteva reinternari si reînregistrarea ei de fiecare data, va arata o tendinta de constanta artificiala. Un parametru legat de functia hepatica, cum ar fi bilirubina totala (BRT), ar putea sa ne intereseze si sa consideram util sa îl înregistram la fiecare reinternare dar nici în acest caz, valorile obtinute nu sunt independente ci mai curând înregistrarea lor este utila pentru urmarirea evolutiei în timp a parametrului BRT. În concluzie, înregistrarea datelor despre un acelasi pacient de mai multe ori este extrem de riscanta pentru acuratetea rezultatelor pe care le obtinem.
7.2 Esantionare
si acum sa trecem la modalitatile prin care se realizeaza inferenta statistica. De la început trebuie precizat ca un rol central îl joaca distributia Gaussiana care de fapt nu este o distributie ca oricare alta ci, datorita proprietatilor ei naturale, în special simetria, are un statut oarecum privilegiat. Pentru a ne da seama de acest lucru, sa presupunem ca ne aflam în fata unei populatii cu un numar foarte mare de indivizi, ceea ce, din punct de vedere statistic se denumeste ca "practic infinita". Sa presupunem pentru simplitate ca media populatiei respective în ceea ce priveste un anumit parametru este m iar deviatia standard este s, valori care pot fi de fapt necunoscute, iar distributia variabilei respective este normala. Sa mai presupunem ca, nestiind statistica, încercam sa aproximam pe m prin medii obtinute pe esantioane de volum mult prea mic, sa zicem de doi indivizi.
Putem chiar sa ne imaginam ce se întâmpla daca luam foarte multe astfel de esantioane, poate chiar pe toate. Vom obtine foarte multe medii aproximative, aproximatii care sunt, multe dintre ele foarte departe de adevarata medie. Vom numi aceste medii aproximative, medii de esantionare de volum 2. Se naste astfel o serie statistica, a acestor medii, care are o importanta deosebita, deoarece are anumite proprietati pe care le vom descrie în continuare, care ne vor ajuta în a estima cât de bune sunt aproximarile prin medii de asantionare.
Fie seria statistica M2: m1, m2, m3.........., seria acestor medii de esantionare de volum 2. Se poate demonstra ca:
"este foarte improbabil ca cele doua loturi sa provina din populatii cu medii egale".
Dar, deoarece nu este exclusa posibilitatea ca cele doua loturi sa provina din populatii cu medii egale, nu putem fi 100% siguri pe decizia luata. În statistica, nu are sens sa se spuna despre o astfel de ipoteza ca este adevarata sau falsa. Tot ce se apreciaza este plauzibilitatea ei.
În statistica, orice afirmatie este mai mult sau mai putin plauzibila, si vom renunta sa o consideram neaparat din punctul de vedere al alegerii între sigur adevarat si sigur fals.
În mod natural, atunci când constatam diferente mari între mediile a doua loturi, punem diferenta pe seama faptului ca populatiile din care provin loturile au medii diferite. Invers, când diferentele între mediile celor doua loturi sunt mici, le punem pe seama întâmplarii si consideram ca loturile provin din populatii cu medii egale, sau, ca provin din aceeasi populatie. Aceasta problema apare foarte des în practica pentru ca foarte des aplicam tratamente la loturi care trebuie apoi comparate cu loturi la care nu se aplica tratamentul.
Sa ne punem deci pentru început problema de a raspunde cât mai precis la întrebarea: mediile reale, ale populatiilor din care provin loturile de mai sus (sanatosi si lacunarism cerebral), sunt egale?
Sa ne reamintim ca daca o variabila este repartizata normal sau Gaussian, cu media m si deviatia standard s, atunci luând loturi de n indivizi din acea populatie, media calculata pe un astfel de lot este o variabila aleatoare care este repartizata tot normal, cu media m si deviatia standard Chiar daca repartitia variabilei nu este Gaussiana, repartitia mediei de esantionare pentru loturi de n indivizi se apropie de una normala cu atât mai mult cu cât n este mai mare. Deci, în aparenta, vom putea estima media reala din parametrii m si sn, asa cum am mai spus, la aproximativ 95% din esantioane, adevarata medie este în intervalul m-2sn, m+2sn si la aproximativ 99% din esantioane adevarata medie este în intervalul m-3sn, m+3sn
Bazat pe aceste observatii care au fost prezentate în capitolul 7, daca vom gasi pentru doua loturi medii care sa dea intervale de încredere care se suprapun, putem decide ca mediile loturilor difera din întâmplare. Daca însa intervalele de încredere nu se suprapun diferenta între medii nu este întâmplatoare, caz în care se spunem ca este semnificativa.
În figurile 8.1 si 8.2, sunt prezentate cele doua cazuri care pot apare în acest tip de problema. În figura 8.1, intervalele de 95% pentru mediile celor doua loturi se suprapun, deci mediile reale ar putea fi egale (diferenta între mediile calculate pe cele doua loturi este probabil întâmplatoare). În figura 8.2 însa, intervalele de 95% pentru mediile celor doua loturi nu se suprapun mediile reale nu ar putea fi egale (adica exista o diferenta între mediile reale, 95% sigur). În felul acesta avem un raspuns destul destul de sigur la întrebarea pusa mai sus.
Figura 8.1 Daca intervalele de 95% pentru mediile a doua loturi se suprapun mediile reale ar putea fi egale, diferenta între mediile calculate pe cele doua loturi este probabil întâmplatoare.
Figura 8.2 Daca intervalele de 95% pentru mediile a doua loturi nu se suprapun mediile reale nu ar putea fi egale, exista o diferenta între mediile reale (95% sigur).
Asa se si procedeaza de fapt, dar numai atunci când sn este cunoscut, adica atunci când s este cunoscut. Acest lucru nu se întâmpla în realitate decât foarte rar, deoarece, asa cum media ne este necunoscuta si încercam sa o estimam, deviatia standard a populatiei ne este cu atât mai putin cunoscuta. În practica, s este înlocuit cu deviatia standard a loturilor pe care se lucreaza, sn, caz în care nu ne mai putem baza pe distibutia Gauss ci pe distributia Student, care difera de la n la n, adica în functie de numarul de indivizi ai esantionului, apropiindu-se de una normala odata cu cresterea lui n. Estimarea mediei se face asemanator, numai ca intervalele difera întrucâtva (a se revedea capitolul 7 pentru amanunte). Deci, un raspuns la întrebarea pusa anterior se poate da cu ajutorul intervalelor de încredere. Mai jos, detaliem discutia despre metode de acest gen, deoarece sunt foarte importante în statistica.
Deci, una din problemele esentiale ale statisticii este aceea de a decide asupra unor ipoteze care se nasc în mod natural din examinarea datelor avute la dispozitie sau a indicatorilor statistici care le caracterizeaza.
În exemplul, de mai sus, masurând latenta semnalului pe nervul optic la indivizi sanatosi, si la pacienti cu lacunarism cerebral si observând o diferenta destul de mare între ele, ne punem intrebarea daca în general lacunarismul cerebral conduce la o latenta mai mare sau, diferenta constatata este o pura întâmplare. De fapt, trebuie sa decidem daca populatiile din care provin cele doua loturi au medii egale sau diferite. Acesta este un tip de problema de baza la care raspund testele statistice.
Vom considera ca normalii la care s-au facut masuratori provin dintr-o populatie, teoretic infinita, pe care o vom denumi populatia normala, iar ceilalti provin in mod asemanator dintr-o populatie pe care o vom denumi populatia afectata. Vom avea doua cazuri:
a) Media latentei la cele doua populatii este aceeasi (necunoscuta) iar diferentele constatate pe cele doua loturi sunt datorate întâmplarii. Daca am continua masuratorile, marind cele doua esantioane, mediile recalculate vor fi mai apropiate, iar in cele din urma vor tinde sa devina egale, rolul întâmplarii diminuându-se încet, încet.
b) Cele doua populatii au medii diferite, si anume cea afectata are o medie a latentei mai mare, caz în care daca am continua masuratorile, marind loturile, încet, încet, mediile tind sa se stabilizeze, adica sa nu se mai modifice prea mult, dar, media la cei afectati tinde la o valoare diferita (si anume mai mare) ca media la sanatosi.
Înainte de a face masuratori efective, nimeni nu poate spune care este situatia, adica nu poate decide între cazurile a) si b). Din pacate, de obicei este greu sa se ia o astfel de decizie chiar si dupa efectuarea de masuratori. In practica, diferente destul de mari între mediile de esantionare pot apare la loturi extrase din aceeasi populatie daca s-au masurat putini indivizi, mai ales daca împrastierea datelor este mare. A trage concluzia ca cele doua loturi provin din populatii cu medii diferite este, bineînteles în acest caz nu numai riscant ci de-a dreptul gresit. Invers, diferente între mediile de esantionare care la prima vedere par neînsemnate, pot sa indice ca cele doua loturi provin din populatii diferite, daca masuratorile s-au facut pe suficient de multi indivizi, mai ales când datele au împrastieri mici.
De exemplu, la un lot de 122 de normali s-a masurat latenta semnalului nervos pe nervul optic si s-a obtinut o medie de 105,4 ms si o deviatie standard de 8,6 ms. Pacientii cu o afectiune au fost 87 si s-a obtinut o medie de 108,7 ms si o deviatie standard de 9,5 ms. Dupa cum se vede foarte usor, diferenta de medie pare mica si suntem tentati sa consideram ca suntem în cazul a), adica diferenta de 108,7 ms - 105,4 ms = 3,3 ms este întâmplatoare. În realitate testul Student, despre care va fi vorba în acest capitol arata ca este aprape sigur (p=99,52%) ca cele doua esantioane provin din populatii diferite sau ca cele doua populatii din care provin (sanatosi si afectati) au medii ale latentei diferite. Acest capitol îsi propune printre altele sa initieze cititorul în modul de a lua astfel de decizii.
Într-un alt caz, pe un lot de 35 de indivizi sanatosi s-a obtinut media de 105,2 ms si o deviatie standard de 11,6 ms în timp ce la cei bolnavi (21), media a fost de 109,6 ms si deviatia standard 13,9 ms. În ciuda faptului ca diferenta este acum ceva mai mare (4,4 ms), si ar trebui deci sa deducem ca este cu atât mai probabil ca cele doua loturi sa provina din populatii diferite, din contra, testul Student arata ca nu sunt suficiente dovezi pentru aceasta concluzie, ci, mai degraba este corect sa punem diferenta constatata pe seama intâmplarii. Acest lucru se întâmpla din cauza datelor mai împrastiate, lucru dovedit de deviatiile standard mai mari, precum si din cauza numarului mai mic de masuratori în cele doua loturi.
Vom conveni în continuare ca, daca ne aflam într-o situatie asemanatoare cu cea de mai sus, sa denumim cele doua situatii posibile (a si b) ca ipoteze fundamentale de lucru si anume pe prima o vom numi ipoteza de diferenta nula, sau ipoteza de nul, iar pe cealalta ca ipoteza alternativa.
Asadar:
Uneori, ca alternative se pot alege doua ipoteze sau chiar mai multe. De exemplu, în cazul de mai sus, putem avea doua ipoteze alternative la ipoteza de nul:
Vom numi test statistic, o metoda care ne ajuta sa decidem cu un grad de siguranta ales, daca ipoteza de nul poate fi respinsa în favoarea ipotezei sau ipotezelor alternative sau daca nu sunt suficiente dovezi care sa justifice respingerea ipotezei de nul.
Ipotezele pe care le putem supune deciziei unui test statistic sunt foarte variate. Din observarea datelor, se pot naste ipoteze dintre cele mai diverse. Categoriile principale de ipoteze sunt:
Fiecare dintre tipurile de ipoteze formulate mai sus, are una sau mai multe ipoteze alternative.
Se poate testa deci, daca dispersiile unor populatii sunt diferite, discutia fiind în fond aceeasi ca la cea pentru medii. În plus, exista teste care testeaza egalitatea a mai multor medii, adica având la dispozitie mediile de esantionare a trei sau chiar mai multe loturi (cu deviatiile lor standard), ne situam în unul din cazurile:
Un test statistic va trebui în toate aceste cazuri, sa ne ajute sa decidem între a respinge sau nu ipoteza de nul H0.
Testarea unor ipoteze statistice se poate face bazându-ne pe proprietatile distributiei normale. De cele mai multe ori insa, ipotezele statistice sunt de asa natura ca este nevoie de cunoasterea proprietatilor altor distributii pentru a putea decide daca sunt sau nu suficient de bine sustinute de datele pe care le avem la dispozitie.
potezei nule este o metoda prin care se specifica multimea valorilor unei variabile aleatoare, pentru care ipoteza H0 trebuie respinsa. Variabila aleatoare folosita, se numeste test statistic, iar multimea valorilor de respingere a lui H0 se numeste regiunea de respingere a testului. Un test este strict determinat de variabila de test si de regiunea de respingere.
În continuare vom expune principalele categorii de teste folosite mai des în practica medicala, dupa care vom da o apreciere a metodelor expuse în acest capitol.
8.2 Teste statistice parametrice de comparare
8.2.1 Testul Student de comparare a unei medii cu media teoretica
Uneori cunoastem din literatura de specialitate care este media populatiei din care presupunem ca este extras un lot si dorim sa verificam ipoteza ca esantionul apartine într-adevar populatiei respective.
Sa presupunem ca este media teoretica si sa presupunem ca valorile masurate pentru indivizii din lotul de comparat dau seria statistica: , iar media de esantionare este . Atunci variabila aleatoare , obtinuta dupa formula:
are o repartitie Student cu n-1 grade de libertate. Decizia o vom lua stabilind care este plauzibilitatea ca sa apartina repartitiei Student cu n-1 grade de libertate. Vom cauta limitele dreapta-stânga între care avem cuprinsa 95% sau 99% din aria de sub crba repartitiei Student. Va fi deci suficient sa cautam valoarea lui , sau , data de tabelele statistice pentru t, si sa o comparam cu valoarea lui
O interpretare, a acestui test este deci urmatoarea:
În figura 8.3, este aratat motivul pentru care comparam cu limita de cuprindere a 95% (99%) din repartitie. Daca este la dreapta acestei limite, este putin probabil sa apartina repartitiei respective si ipoteza H0 va fi respinsa ca falsa.
Figura 8.3 Pragul de 95% arata ca valori mai mici decât acest prag sunt plauzibile, iar valori mai mari decât acest prag sunt neplauzibile.
Exemplu practic:
Deci, calculam valoarea lui tc :
Deoarece tt < tc, luam decizia ca diferenta între media de esantionare si media propusa de ipoteza este semnificativa cu pragul de semnificatie de 95%
8.2.2 Testul z pentru compararea unei medii de esantionare cu o medie teoretica când dispersia teoretica este cunoscuta
Este cazul când este cunoscuta si deviatia standard teoretica s. Statistica
are o distributie care se apropie de distributia normala cu media 0 si abaterea standard 1. În figura 8.4, este aratat modul cum se alege pragul de semnificatie.
Figura 8.4 Alegerea pragului de semnificatie de 95% pentru testul z de comparare a unei medii de esantionare cu o medie teoretica când dispersia teoretica este cunoscuta
Se observa din figura 8.4, ca testul se bazeaza pe proprietatea distibutiei Gauss standard ca între -1,96 si 1,96 margineste sub curba 95% din aria egala cu 1 sau 100%, marginita de întreaga curba si axa orizontala.
Exemplu de calcul:
Se stie ca pe un lot reprezentativ de pacienti bolnavi de meningita, în anul trecut, s-a obtinut o medie latentei semnalului nervos pe nervul optic, de la retina la lobul occipital, de 105ms iar abaterea standard 8,5ms. Pe un esantion de 54 de pacienti bolnavi de meningita de diverse etiologii, s-a obtinut anul acesta o medie a latentei de 109,3ms. Sa se testeze daca media obtinuta compatibila cu cea de anul trecut la un prag de semnificatie de 95%.
Testarea se face prin calculul lui zc si compararea cu 1,96.
Deoarece valoarea statisticii întrece pragul theoretic, ipoteza de nul se respinge la pragul de semnificatie de 95%. Media calculata pe esantionul de 54 de pacienti nu este compatibila cu media luata ca teoretica. Explicatia ar putea fi ca lotul de 54 de pacienti luat în studiu nu este reprezentativ, probabil din cauza faptului ca a continut un procent prea mare de tipuri de meningite care modifica latenta.
8.2.3 Testul Student de comparare a mediilor. Cazul esantioanelor mari.
Vom face urmatoarele conventii pentru o mai buna întelegere:
Ipotezele sub care lucreaza testul sunt:
Testul se bazeaza pe statistica:
care are o repartitie Gauss standard. Din tabele se ia pragul teoretic de 95% (sau de 99%), care este 1,96 (respectiv, 2,57).
Decizie:
Exemplu de calcul:
Determinari ale latentei semnalului nervos pe nervul optic la pacienti cu scleroza multipla si la normali, au aratat urmatoarele:
|
|
Volumul lotului |
Media de esantionare |
Deviatia standard |
|
Sanatosi |
|
|
|
|
Scleroza |
|
|
|
Ipotezele sunt:
Statistica testului este: . Deoarece este mai mare decât pragul de 1,96, ipoteza de nul se respinge, diferenta între cele doua medii de esantionare este semnificativa la pragul de semnificatie de 95%
8.2.4 Testul Student de comparare a mediilor. Cazul esantioanelor mici si dispersii egale
Fie seriile statistice:
, extras din populatia cu media m1 si dispersia s2 si
extras din populatia cu media m2 si dispersia s2
Asadar, avem doua medii de esantionare, si , doua deviatii standard de esantionare si, iar ipotezele pe care le facem sunt:
Daca populatiile sunt de aceeasi dispersie, atunci putem amesteca cele doua esantioane si sa estimam s2 prin dispersia de esantionare calculata luând în considerare ambele esantioane:
sau cum se poate scrie mai pe scurt:
unde la numitor s-a luat n1+n2-2, deoarece mediile celor doua loturi sunt doi parametri care se cunosc si deci trebuie sa scadem 2 din numarul de grade de libertate.
Cum din formulele de calcul pentru si , avem:
si
vom pune în formula lui la numarator, in locul celor doua sume care se aduna, expresiile si . Deci, formula de calcul a dispersiei comune de esantionare este:
Testul se bazeaza pe statistica
care are o distributie Student cu n1+n2-2 grade de libertate.
Pentru a alege între ipotezele H0 si H1, ne folosim de aceasta statistica. Decizia este:
Sa mai amintim ca am folosit tacit ipoteza ca masuratorile efectuate pe indivizii din lot sunt independente, adica nu depind unele de altele ceea ce de fapt se si întâmpla în majoritatea cazurilor când este vorba de esantioane de pacienti.
Astfel, testul Student pentru loturi mici poate fi aplicat daca sunt îndeplinite urmatoarele conditii, numite conditii de aplicare pentru teste parametrice:
Exemplu de calcul:
Masurând frecventa cardiaca la 9 pacienti cu hipertiroidie si la alti 9 pacienti cu hipotiroidie, au fost obtinute valorile din tabelul 8.1. Primul pas este calculul mediilor, al deviatiilor standard si al dispersiilor. Cum statistica testului foloseste direct dispersiile, deviatiile standard nu sunt absolut necesare.
Tabelul 8.1 Valorile frecventei cardiace la 9 pacienti cu hipotiroidie si 9 pacienti cu hipertiroidie. Mediile, deviatiile standard si dispersiile sunt calculate
pe ultimele trei linii
Calculele, decurg în felul urmator:
Valoarea prag a lui t95% din tabele statistice este 2,12. Cum statistica testului depaseste valoarea prag, ipoteza de nul se respinge, diferenta între cele doua medii de esantionare este semnificativa la pragul de semnificatie de 95%.
8.2.5 Testul ANOVA
Este tot un test de comparare a mediilor, dar are avantajul ca poate compara în acelasi timp mediile mai multor loturi, in vreme ce testul Student nu poate face acest lucru. Masuratorile se fac deci pe mai multe loturi pe care dorim sa le comparam din punct de vedere al mediilor, ipotezele pentru acest test fiind:
Deoarece statistica testului ANOVA urmeaza o repartitie Fisher, pe care nu am prezentat-o în aceasta carte, vom discuta numai interpretarea testului în cazul în care este efectuat cu ajutorul unui program de calculator.
Rezultatul p, al testului, furnizat de program, are aceeasi interpretare ca si la celelalte teste statistice:
Aceste test are dezavantajul ca, în cazul în care diferenta între medii este semnificativa, nu preizeaza care pereche de medii difera semnificativ si raspunsul la aceasta întrebare trebuie cautat prin teste pe perechi de loturi.
Exemplu de utilizare a pachetului Excel:
În trei comune ale judetului Dolj au fost luate date despre obiceiurile alimentare si legatura lor cu obezitatea si diabetul. Printre alte date s-au cules si greutatea indivizilor precum si date despre fumat. Indivizii, indiferent de sex sau grupa de vârsta au fost împartiti în patru categorii: nefumatori, fosti fumatori, usor fumatori (sub 10 tigarete pe zi) si fumatori (peste 10 tigarete pe zi). Înregistrarea acestor date s-a facut cu scopul de a stabili daca exista o legatura între obiceiul fumatului si greutatea corporala la acesti indivizi. Ipotezele testului sunt:
În figura 8.5, este aratat modul cum au fost introduse datele si raspunsul programului Excel la cererea de a compara mediile cu ajutorul testului ANOVA. Pe coloanele B, C, D si E sunt introduse greutatile indivizilor din fiecare categorie, iar în dreapta se gaseste raspunsul programului, care da date sumare despre loturi (volum, medie, dispersie, etc), precum si rezultatul p al analizei pe care a executat-o (p-value, marcat cu gri în figura)
Cum rezultatul testului este p=0,00176, adica, exprimat în procente este p=0,176%, decizia este: exista o diferenta înalt semnificativa între mediile loturilor. Concluzia este ca greutatea corporala la acesti indivizi depinde înalt semnificativ de tipul de fumat.
Figura 8.5 Folosirea programului Excel pentru efectuarea testului ANOVA
9 Corelatii
9.1 Introducere
Organismul uman este de departe cel mai complex sistem cunoscut de noi în univers. În functionarea unui sistem sunt importante cunoasterea parametrilor de functionare ai acestuia. De-a lungul timpului, oamenii de stiinta au studiat sistemele considerând ca acestea sunt caracterizate de un numar mai mic sau mai mare de asa-numiti parametri interni ai sistemului care caracterizeaza starea acestuia.
În functie de starea sistemului la un moment dat, el poate reactiona într-un fel sau altul la asa-numitele variabile de intrare, facând sistemul sa treaca într-o alta stare si, eventual sa produca anumite variabile de iesire. Daca ar fi sa facem o paralela, atunci pentru organismul uman variabilele de intrare sunt conditiile de mediu, atât cele care se refera la conditiile în care organismul traieste si îsi desfasoara activitatea cât si actiuni mai mult sau mai putin momentane asupra lui cum ar fi actiunile permanente si vitale ca satisfacerea nevoilor de sete, foame, relatiile cu semenii, etc. Parametrii interni ar fi, daca am continua aceasta paralela, toate acele marimi care caracterizeaza starea organismului atât momentan cât si ca evolutie în timp. Variabilele de iesire ar fi actiunile fiintei umane ca raspuns la conditiile de mediu.
Aceasta paralela ar putea fi continuata printr-un studiu mai amanuntit al interrelatiilor care se nasc în mod natural între toate variabilele de intrare si de iesire, conditionate mai mult sau mai putin de parametrii interni. Din pacate acest mod de abordare a organismului uman pune probleme atât de complexe încât rezultatele concrete care eventual s-ar putea obtine dintr-o astfel de abordare s-ar lasa foarte mult asteptate.Organismul uman este atât de complex încât nu se poate pune problema de a îl cuprinde în ecuatii si formule oricât de complexe, cuprinzatoare si numeroase ar fi ele.
De aceea, suntem obligati la a aborda un eventual studiu din perspectiva teoriei sistemelor al organismului uman sa procedam simplificator si sa încercam:
9.2 Notiunea de corelatie
Functionarea organismul ca un tot unitar este conditionata de conlucrarea într-o armonie perfecta a unei miriade de factori, multi dintre ei înca necunoscuti. Legaturile dintre ei sunt de o complexitate ce ne scapa deocamdata pe alocuri. Cunoasterea umana, cu toate progresele facute, a reusit sa dezvaluie ceea ce am putea numi valul exterior al proceselor complexe din organism. Ramân de studiat corelatii pe care acum nici nu le banuim sau pe care le cunoastem doar superficial si trebuie sa le aprofundam.
Pentru a explica notiunea de corelatie, vom exemplifica câteva legaturi între parametri de macrosistem, adica parametri ce caracterizeaza organismul în totalitatea lui sau sistemele mai importante din organism. Astfel, stim cu totii ca exista o corelatie între tensiunea arteriala sistolica si cea diastolica. Ce înseamna acest fapt? Înseamna ca tendinta de crestere a tensiunii sistolice, este însotita de o tendinta de crestere si a tensiunii diastolice, iar tendinta de scadere a primeia este însotita de o tendinta de scadere a celei de-a doua.
Tot astfel, alte perechi de parametri manifesta o comportare asemanatoare: greutatea si înaltimea, numarul de eritrocite si hemoglobina, vitezele de sedimentare a hematiilor la o ora si la doua ore, colesterolemia si lipemia, etc. Trebuie subliniat ca variatia concomitenta a celor doi parametri se manifesta numai ca tendinta, nu este o regula. Pot exista indivizi cu tensiunea sistolica foarte mare si cea diastolica normala sau invers, indivizi cu tensiunea sistolica normala si cea diastolica scazuta. Totusi, majoritatea indivizilor manifesta tendinta de a avea valori crescute sau scazute, pentru ambele concomitent.
Vom spune ca doi parametri care au tendinta de a creste sau descreste simultan sunt direct corelati.
Asa cum a fost data mai sus, notiunea de corelatie se refera la tendinta de crestere sau descrestere simultana a doi parametri indiferent cît de puternica sau de slaba este aceasta tendinta. Vom vedea mai departe ca este nevoie de o cuantificare a tariei corelatiei între doi parametri, altfel discutiile nu pot fi nuantate si corelatia ar fi o notiune prea putin utila.
Pe de alta parte, exista cazuri în care doi parametri se coreleaza prin cresterea unuia însotita de o tendinta de descrestere a celuilalt. Astfel, cresterea concentratiei hormonului tiroidian T4, este însotita de o scadere a frecventei cardiace. Acesti doi parametri sunt un exemplu de corelatie inversa.
Vom spune ca doi parametri sunt corelati invers daca au tendinta ca, odata cu cresterea sau descresterea unuia, celalalt sa descreasca sau sa creasca. (au tendinta inversa de variatie).
Trebuie facute câteva observatii care sa clarifice cele introduse mai sus si sa evite o folosire abuziva a termenului de corelatie:
Tendinta de corelatie o putem întelege în mai multe sensuri dintre care doua intereseaza mai mult domeniul medicinii:
Exemple de situatii în care avem corelatie între doi parametri sunt redate în figurile 9.1, 9.2 si 9.3. În figura 9.1, sunt reprezentate valorile bilirubinei totale si ale bilirubinei directe la 235 de pacienti cu ciroze hepatice si cancer hepatic. Se observa o corelatie extrem de puternica, din forma norului de puncte care este extrem de alungit si subtire.
Figura 9.1 Valorile bilirubinei totale si ale bilirubinei directe la 235 de pacienti cu ciroze hepatice si cancer hepatic. Se observa o corelatie extrem de puternica, din forma norului de puncte care este extrem de alungit si subtire
Figura 9.2 Valorile pentru hormonul tiroidian T4 si cele ale hormonului T3, la 9 pacienti cu hipertiroidie si 9 pacienti hipotiroidie. Valorile sunt puternic corelate, fapt care se observa din forma norului dublu de puncte care se aliniaza de-a lungul unei linii aproape drepte.
În figura 9.3 este dat un alt exemplu de pereche de parametri care se coreleaza puternic: VSH la o ora si VSH la doua ore. Norul foarte alungit si subtire, arata tendinta de corelatie. Cele câteva puncte care sunt mult în afar norului, tradeaza erori de introducere adatelor. Acest exemplu ne spune si ca unele din valorile aberante pot fi oservate pe graficul de corelatie.
Figura 9.3 VSH la o ora si VSH la doua ore. Norul foarte alungit si subtire, arata tendinta de corelatie
Figura 9.4 Valorile sodiului seric si potasiului seric la 235 de pacienti cu afectiuni hepato-renale. Nu exista corelatie, deoarece punctele norului sunt distribuite întâmplator.
daca esantionul pe care s-au facut masuratorile este omogen sau este eterogen (Omogenitatea).
Exemple:
Tensiunea sistolica TMAX: 170, 160, 160, 150, 150, 170, 160, 180, 150, 150.
Se observa ca pentru calculul lui r avem nevoie de mediile celor doua serii statistice, si , si pentru fiecare pacient în parte de diferentele si , care pentru numarator trebuie înmultite între ele, iar pentru numitor trebuie ridicate la patrat si apoi sumate pentru toti pacientii. Deoarece valorile au fost alese special ca sa se usureze calculele, se observa ca mediile pentru TAMAX si TAMIN sunt =160 si =80. Este bine ca toate calculele necesare pentru gasirea lui r sa fie organizate într-un tabel asa cum se vede în tabelul 9.1:
Tabelul 9.1 Calculul coeficientului de corelatie Pearson
|
|
|
Valorile pentru TAMAX |
|
|
|
Valorile pentru TAMIN |
|
|
|
Diferentele pentru TAMAX |
|
|
|
Diferentele pentru TAMIN |
|
|
|
|
|
|
|
|
|
|
|
|
Calculul lui r este:
Trecând peste faptul ca de obicei calculele sunt putin mai dificile din cauza unor zecimale care apar inerent la calculul mediilor si deci al diferentelor, sa cautam sa vedem ce se poate întâmpla în diverse situatii ce pot apare în legatura cu valorile luate de cei doi parametri. În primul rân sa observam ca la numarator, în cazul nostru, numarul 350 a fost obtinut prin adunarea unor numere pozitive si anume 5x50+100. Dar observam ca valoarea 50 obtinuta pentru al patrulea pacient (ca si la al noualea si al zecelea, de altfel) s-au înmultit doua numere negative, pe când la celelalte valori diferite de 0, la pacientii 1, 6 si 8, numerele au fost obtinute prin înmultirea unor numere pozitive. Acest lucru nu este nici pe de parte lipsit de importanta, ci din contra, este ceea ce caracterizeaza situatia prezentata în mod fundamental.
Sa facem urmatoarele observatii referitoare la cazul prezentat:
Ceea ce am precizat în rândurile de mai sus este caracteristic pentru situatiile în care cei doi parametri se coreleaza: cei doi parametri iau valori preponderent în acelasi sens, adica ori ambii sub medie, ori ambii peste medie.
Din cauza tendintei a doi parametri care se coreleaza direct, ca atunci când unul este crescut, sa fie si celalalt crescut, vom fi pentru majoritatea pacientilor în situatii ca mai sus si produsele care se aduna la numarator sunt preponderent pozitive. În acest caz, suma de la numarator tinde sa aiba valori pozitive crescute. Evident, corelatia dintre parametri este doar o tendinta si este probabil sa întâlnim pacienti care, desi au unul din parametri crescut, de exemplu peste medie, celalalt poate sa nu fie crescut, chiar sa fie sub medie, caz în care produsul corespunzator lui va fi negativ. Dar acest fenomen nu este o tendinta daca parametrii sunt corelati ci mai curând accident. Suma obtinuta la numarator va avea tendinta de a lua valori mari si pozitive în ciuda unor astfel de accidente.
Daca cei doi parametri sunt corelati invers, adica tendinta unuia de a avea valori crescute este însotita de tendinta celuilalt de a avea valori scazute, în acest caz, predominante vor fi situatiile în care în produsul , ia des valori negative. Într-adevar, daca un parametru are valori sub medie si celalalt peste medie, o paranteza va fi pozitiva si una negativa. Daca acest fapt este o tendinta, parantezele de la numarator vor fi cele mai multe negative. Suma obtinuta la numarator va avea tendinta de a lua valori mari si negative.
Daca cei doi parametri nu sunt corelati, parantezele de la numarator vor avea semne aleatorii, vor fi unele produse pozitive si unele negative. Tendinta va fi ca cele negative si cele pozitive sa se anuleze unele pe altele. Suma obtinuta la numarator va avea tendinta de a lua valori mici, pozitive sau negative.
Nu am discutat nimic despre numitorul coeficientului r, deoarece el are totdeauna semnul +, iar rolul lui este numai de a face ca r sa fie cuprins între -1 si +1. Magnitudinea lui r, precum si semnul sau, sunt dictate de suma de la numarator. Asadar, orice valori ar lua cei doi parametri, prin calculul lui r, obtinem un numar real cuprins în intervalul de numere reale [-1, 1].
Interpretarea coeficientului de corelatie Pearson se face în termeni extrem de subiectivi si imprecis astfel:
La fel, pentru valori negative pentru anticorelatie (corelatie inversa).
O interpretare obiectiva a lui r este tinând cont de semnificatia lui statistica, care este prezentata în subcapitolul urmator.
9.4 Testarea semnificatiei statistice a lui r
9.5 Notiunea de dreapta de regresie
Daca doi parametri sunt suficient de puternic corelati, atunci cunoscând valoarea unuia dintre ei, celalalt nu ia valori absolut aleatorii ci valoarea pe care acesta o poate lua este într-o legatura mai puternica sau mai slaba cu valoarea primului, în functie de cât de puternic este coeficientul de corelatie între cei doi parametri.
Sa privim putin mai atent pe un grafic (vezi figura 9.6), ce se întâmpla în cazul unei corelatii puternice. Anume, sa reprezentam pe orizontala valorile latentei undei P100 pentru ochiul drept (LD), iar pe verticala valorile latentei undei P100 pentru ochiul stâng (LS), la 913 de pacienti, masurate în milisecunde.
Figura 9.6 Corelatia valorilor latentei undei P100 pentru ochiul drept (verticala) si valorile latentei undei P100 pentru ochiul stâng (orizontala), la 913 de pacienti, masurate în milisecunde. Fiecare punct de pe grafic corespunde unui pacient. Se observa o corelatie puternica din aranjarea norului de puncte, care are o forma alungita.
Asa cum era de asteptat valorile LD si LS se coreleaza, în sensul ca au tendinta de a se aseza într-un nor alungit dinspre stânga jos spre dreapta sus pe grafic, cu unele exceptii, reprezentate de punctele care sunt iesite din nor. De fapt, se observa ca majoritatea punctelor din grafic se aranjaza într-o zona ovala.
În cazurile ca cel din figura 9.6, se poate încerca gasirea unei drepte care sa treaca cât mai aproape de punctele graficului, dreapta care sa reprezinte o legatura între cei doi parametri. În figura 9.7 este reprezentata o astfel de dreapta pentru graficul din figura 9.6. Aceasta dreapta exista pentru nori de puncte foarte diversi, si se numeste dreapta de regresie.
Figura 9.7 Dreapta de regresie pentru cazul latentei semnalului nervos pe cei doi ochi, la apcienti cu diverse afectiuni. Pe orizontala, valorile pentru ochiul stâng, iar pe verticala cele pentru ochiul drept.
Numim aceasta dreapta legatura între cei doi parametri în sensul urmator: daca se cunoaste valoarea de pe orizontala, se poate calcula cu oarecare aproximare valoarea de pe verticala, si invers. În exemplul din figura 9.7, daca stim latenta pentru ochiul stâng, putem calcula cu o anumita aproximatie latenta pentru ochiul drept, si invers. Acest fapt este sugerat în figura 9.8, de sagetile care indica valoarea aproximativa de pe o axa, corespunzatoare unei anumite valori de pe cealalta axa.
Figura 9.8 Folosirea dreptei de regresie ca legatura între cei doi parametri care sunt puternic corelati
Dreapta de regresie este de obicei cautata prin asa-numita metoda a celor mai mici patrate, expusa în subcapitolul urmator.
9.6 Metoda celor mai mici patrate (MCMMP)
Vom cauta o dreapta care sa se apropie cât mai mult de punctele graficului, dreapta care o vom numi drepta de regresie liniara. Pentru a ne da seama cum intrepretam expresia "se apropie cât mai mult de punctele graficului", sa luam un exemplu simplu, ca cel din figura 9.9.
Figura 9.9 O dreapa de regresie se cauta ac dreapta care este situata cât mai aproape de punctele graficului. Distantele de la punctele graficului la dreapta se masoara pe verticala. În imagine, distentele care trebuie sa fie cât mai mici sunt segmente verticale
Vom spune ca o dreapta este dreapta de regresie daca suma distantelor de la puncte la dreapta, masurate pe verticala si ridicate la patrat, este minima.
Dreapta pe care o cautam are ecuatia , si vom întelege prin aceasta ca, odata cunoscuta valoarea parametrului de pe abscisa, x, putem calcula valoarea parametrului de pe ordonata, y, prin înmultirea cu a si adunarea lui b. Asadar, gasirea dreptei de regresie este echivelenta cu gasirea coeficientilor a si b. În figura 9.10 este prezentata o situatie în care dreapta de regresie poate fi folositî pentru aproximarea unui efect Y (care poate fi un rezultat al unei medicatii) în functie de o cauza X (care poate fi medicasia). Se observa ca putem gasi nivelul efectului dupa valoarea luata de factorul cauza. Pentru valoarea 10 a lui X, efectul Y are valoarea aproximativa 1010. Pentru valoarea 50 a lui X, Y ia valoarea 925.
Figura 9.10 Dreapta de regresie ca legatura între cauza si efect. Se observa ca putem gasi nivelul efectului dupa valoarea luata de factorul cauza. Pentru valoarea 10 a lui X, efectul Y are valoarea aproximativa 1010. Pentru valoarea 50 a lui X, Y ia valoarea 925
Proprietatea de baza a dreptei de regresie, se scrie astfel:
ceea ce exprima faptul ca segmentele ce unesc fiecare punct cu punctele de pe dreapta situate pe aceeasi verticala, trebuie sa fie cât mai scurte posibil. Exprimarea aceasta nu este tocmai corecta, ci mai degraba intuitiva, caci, a spune ca segmentele sunt cât mai scurte, nu precizeaza nimic când se refera la toate segmentele. Nu vom sti exact care dintre ele trebuie sa fie mai scurt si care mai lung când suma patratelor lor este minima.
Vom interpreta expresia de mai sus ca o expresie ce contine doua necunoscute, si anume a si b, si dorim aflarea lor pentru a putea fi utilizate în ecuatia , atunci când avem nevoie.
Minimul expresiei ce are ca variabile pe a si pe b, se poate afla printr-un procedeu care este cunoscut din analiza matematica, si anume, minimul unei functii se realizeaza pentru acele valori ale necunoscutei care anuleaza derivata întâi a functiei în raport cu variabila respectiva. În cazul în care avem o functie cu doua variabile, ca cea de mai sus, va trebui sa anulam derivatele ei în raport cu fiecare dintre cele doua necunoscute. Vom scrie deci expresia S astfel ca derivarea în raport cu a si cu b sa fie cât mai facila.
Pentru aceasta, vom folosi formula
precum si faptul ca o suma poate fi distribuita, adica este valabila formula:
Astfel vom avea:
si dupa distribuirea de care vorbeam mai sus:
sau, dupa ce scoatem în fata sumelor ceea ce nu depinde de i:
Acum sa nu uitam ca si sunt valorile masurate ale celor doi parametri, care dau pozitiile punctelor de pe grafic, si deci, fiind cunoscute, sumele din expresia lui S sunt cunoscute. De fapt, se obisnuieste ca aceste sume sa fie notate cu urmatoarele notatii, mult folosite în analiza de regresie:
Asadar, sunt numere cunoscute în momentul calculului de care ne ocupam ceea ce face ca expresia lui S sa devina:
Acum pentru a afla minimul lui S vom deriva odata în raport cu a si vom egala cu 0 ceea ce am obtinut, apoi vom deriva în raport cu b si vom egala cu 0 ceea ce am obtinut. Nu trebuie uitat ca, la derivarea în raport cu a, vom considera ca b este constanta si invers. Vom obtine deci relatiile:
si
care se vede ca pot fi rescrise ca un sistem de doua ecuatii cu doua necunoscute, în felul urmator:
sau, dupa trecerea termenilor care nu depind de necunoscutele a si b în partea dreapta si împartirea cu 2 a ambelor egalitati, obtinem:
Acesta este, dupa cum se poate usor observa, un sistem de doua ecuatii cu doua necunoscute, chiar în forma cea mai simpla (sistem liniar).
Metoda expusa mai sus se numeste Metoda Celor Mai Mici Patrate (MCMMP), si este mult folosita pentru simplitatea cu care ne pune la dispozitie un rezultat util. Utilitatea acestei metode este mai clar pusa în evidenta atunci când o folosim pentru evaluarea unui efect cuantificabil când cauzele care îl produc pot fi cuantificate suficient de bine. Un bun exemplu este aplicarea unui tratament cu un medicament în diferite doze, daca efectul acestuia este suficient de obiectiv cuantificabil.
Alt exemplu de aplicare utila a metodei celor mai mici patrate este estimarea evolutiei în timp a unor fenomene de intensitate cuantificabila. De exemplu, atunci când am înregistrat numarul anual de cazuri de cancer de sân într-o arie geografica data, si ne punem problema daca este îndreptatita ipoteza unei tendinte de crestere a incidentei acestei maladii. În acest caz, dreapta de regresie este un estimator al vitezei de crestere a incidentei si se poate testa daca exista o crestere semnificativa, iar în caz afirmativ se poate estima cantitativ aceasta tendinta.
9.7 Regresii neliniare
Exista cazuri când dependenta între un efect si o cauza, sau în general între doi parametri nu este liniara. De exemplu, efectul poate sa sufere un fenomen de quasi saturatie si la un moment dat, desi doza creste semnificativ, efectul are o crestere aproape insesizabila, sau invers, la cresteri limitate ale dozei, efectul tinde sa creasca foarte mult. În realitate se pot întâlni extrem de multe astfel de situatii. În aceste cazuri, se cauta nu drepte de regresie ci alte curbe, dupa caz, logaritmice, exponentiale, polinomiale, etc.
Cea mai simpla generalizare este cazul polinomului de gradul al doilea:
caz în care, în mod evident trebuie gasiti trei coeficienti în loc de doi. Cantitatea de minimizat este
În acest caz, cei trei coeficienti sunt solutiile unui sistem de trei ecuatii cu trei necunoscute, obtinute din egalarea cu 0 a celor trei derivate partiale ale lui S în raport cu a, b si respectiv c:
Au fost folosite si regresii cu polinoame de ordin mai mare, însa pentru a presupune ca între doi parametri este o legatura foarte complexa trebuie puternice dovezi teoretice, care de obicei nu ne stau la dispozitie.
|