Statistika

Zkoumá společenské jevy na dostatečně rozsáhlém souboru případů a hledá ty vlastnosti jevů, které se projevují teprve v souboru případů, nikoli na jednom případě.

Statistický soubor - mnozina vsech objektů statistického pozorování (osob, věcí, jevů) shromázděných na základě toho, 252f519c ze mají jisté společné vlastnosti.

Statistické jednotky prvky statistického souboru. Jejich počet značíme n

Statistický znak - společná vlastnost statistických jednotek jejíz proměnnost je předmětem statistického zkoumání.

Hodnoty znaku - jednotlivé údaje statistického znaku. Značí se x₁, x₂, x₃, ..... x_n. Znaky kvantitativní mají hodnoty vyjádřeny čísly (např. výska, váha, počet záků...), znaky kvalitativní slovním popisem (např. muz - zena, národnost,...)

Absolutní četnost hodnoty znaku x_j je číslo, které udává, kolikrát se v souboru M vyskytuje hodnota znaku x_j. Značí se n_j. Součet absolutních četností se rovná počtu jednotek souboru.

Relativní četnost hodnoty znaku x_j je dána podílem , kde n_j je absolutní četnost hodnoty znaku x_j,  n rozsah souboru M (počet vsech jednotek v souboru). Udává se zpravidla v procentech: . Součet relativních četností se rovná 1

Diagramy - 1) Spojnicový diagram (polygon četností)

2) Kruhový diagram

3) Sloupcový diagram

Charakteristika polohy hodnot znaku - jsou to čísla, která určitým způsobem charakterizují průměrnou hodnotu sledovaného kvantitativního znaku.

Aritmetický průměr: podíl součtu hodnot znaku a jeich počtu:

Vázený aritmetický průměr: mají-li hodnoty x_i četnost n_i:

Geometrický průměr:

Harmonický průměr: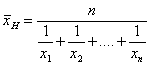

Medián: prostřední člen mezi hodnotami x_i, jsou-li uspořádány podle velikosti. Označení med (x)

n-liché - - bereme prostřední znak

n-sudé -

Modus: hodnota s největsí četností

Charakteristika variability hodnot znaku - jak se hodnoty znaků prvků souboru M lisí od zvolené charakteristiky polohy, resp. od sebe navzájem.

Variační rozpětí: rozdíl mezi největsí a nejmensí hodnotou znaku prvků daného souboru M

R: x_max - x_min

Průměrná absolutní odchylka: aritmetický průměr absolutních hodnot odchylek hodnot znaků vsech prvků od aritmetického průměru hodnot znaku:

(10=n)

Rozptyl: aritmetický průměr druhých mocnin odchylek hodnot znaku od aritmetického průměru

Směrodatná odchylka: druhá odmocnina z rozptylu: Sx=

Variační koeficient - podíl směrodatné odchylky a aritmetického průměru. Má smysl jen tehdy, nabývá-li znak x nazáporných hodnot (kladné bez 0)

Mezikvartelová odchylka -

Pokud je dělitelno 4: 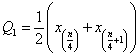Není dělitelno 4: Q₁=x(n₁)

n₁=číslo zaokrouhleno na nejblizsí celé číslo

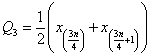Q₃=x (n₃) n₃=

Př. n=20

Koeficient korelace: zjisťuje, zda jsou na sebe závislé dva znaky x a y (např. výska a váha osob). Vzdy platí |r| 1. Čím více se tato hodnota blízí víc k 1, tím povazujeme závislost x, y za větsí.

(s_x - směrodatná odchylka)
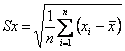
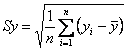