DREHSTROMNETZ

Das Drehstromnetz besteht aus einzelnen elektrischen Betriebsmitteln, die in einer bestimmten topologischen Anordnung zu einem Netz zusammengeschaltet sind.

Um das elektrische Verhalten des Netzes, im störungsfreien oder gestörten Betrieb beurteilen zu können, ist es notwendig das Drehstromnetz mit seinen Betriebsmitteln in ein Modell überführen, das der Berechnung zugänglich ist.

Dieses Vergehen wird sowohl bei der Plannungsarbeiten als auch für Betriebsberechnungen angewendet.

3.1 Freileitungen

Freileitungen machen meistens eine elektrische Verbindung zwischen Erzeugungs- und Verbrauchungsort. Zwischen diesen Orten kann mehrere Hundert km sein (Bild 3.1).

Bei der Bau einer Freileitung sollen folgende wichtige Problemen gelösst sein:

Festlegung der Leitungsführung (Trasee) mit Mastaufteilung;

Wahl des Leiterquerschnittes, des Leitermaterials, den Isolatoren und Armaturen;

Festlegung des Mastkopfbildes, Wahl der Mastart und Berechnung der Maste;

Gründung der Maste;

Erdung der Maste.

Erst nach sorgfältig durchgeführter Planung und Bauvorbereitung kann mit dem Bau der Freileitung begonnen werden.

Die Leitungsführung (Trasee) wird in erster Linie durch die Geländehindernisse (Wald, Dörfer, Flussläufe usw.) und die Möglichkeiten die Masten zu gestellen bestimmt.

Massgebend für die Bemessung einer Freileitung in elektrischer Hinsicht sind, wegen der meist grossen Übertragungsentfernungen, die zulässige Werte für Spannungsfall und Leistungsverlust.

Von einer elektrischen Leitung sind im wesentlichen vier Forderungen zu erfühlen:

die mechanische Festigkeit muss gewährleistet sein; besondere Festigkeits­rechnungen sind aber nur bei Freileitungen notwendig;

die Temperaturerhöhung muss in ungefährlichen Grenzen bleiben; diese Forderung muss für alle stromduchgeflössenden Bestandteile erfühlt wird;

die Leitungsverluste sollen einen verträgbaren Umfang nicht überschreiten.

die Spannungsqualität soll in die bestimmte Grenze bleiben (die Spannungabweichung, die Oberwellengehalt wegen der Korona­erscheinung , Spannungsunterbrechung).

3.1.1 Maste

Als Stützpünkte für Freileitungen dienen Maste verschiedener Konstruktions­arten. Längs einer Leitungsstrasse unterscheidet man:

Tragmaste, die in der Flucht der Leitung stehen und normalerweise nur als Tragpunkte dienen;

Abspannmaste an denen die Leiter abgespannt sind;

Spezialmaste (Winkel-, End oder Abzweigpunkte).

Als Beispiel, Bild 3.2 zeigt einen 110 kV- Tragmast mit zwei Stromkreisen und einem Erdseil und einen 400 kV- Tragmast auch mit zwei Stromkreisen und einem Erdseil.

Für Ausbildung des Mastkopfbildes (Bild 3.3) sollen Mindestabstände der unter Einwirkung des Windes ausgeschwungenen Leiterseile, Bemessungs­spannung der Leitung, auftretende Überspanungen sowie die örtliche Gelände­verhältnisse massgebend.

Maste für Freileitungen mit Bemessungsspannungen von 110 kV und mehr werden in der Regel als Gitterkonstruktionen aus Winkelstählen oder aus Stahlrohren ausgeführt. Für Freileitungen mit der Bemessungsspannung kleiner als 110 kV benutzt man meistens Stahlbetonmaste oder Holzmaste.

3.1.2 Stromleiter

In zunehmenedem Masse hat sich das Aluminium-Stahl-Seil für Stromleiter und Stahl-Seil für Erdleiter durchgesetzt.

f = 9,2 m

6 m

Erdseil

~ 300 m

5,9 m

8,9 m

3,5 m

4,2 m

1,8 m

4,2 m

15,2 m

28,9 m

a)

9,75 m

8 m

4,8 m

8 m

21,2 m

52 m

14 m

22 m

8 m

f = 13,2 m

~ 500 m

b)

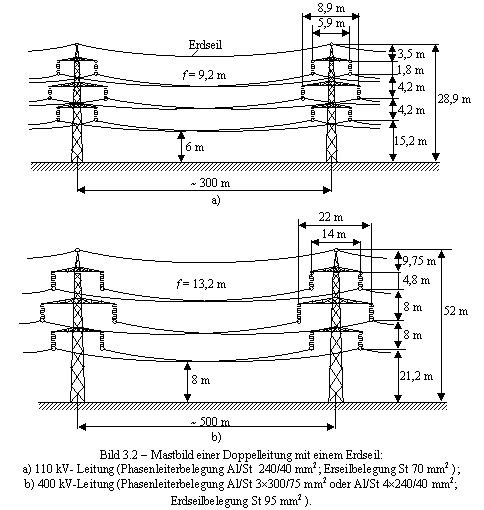
Gründung

Mastschaft

Gabel

Isolatorkette

Stromleiter

Erdseilspitze

Erdseil

Querträger

Bild 3.3 Tragmast mit einem Stromkreis und zwei Erdseilen.

Bild 3.4 Der Aufbau des Al-St 300/69 mm2 Seiles.

Al

St

Al-St Seile bestehen aus verseiltem Aluminiummantel mit Stahlkern zur Erhöhung der Zugfestigkeit. Die Seile werden durch Material und Querschnitt in mm² gekennzeichnet. Bild 3.4 zeigt den Aufbau eines Aluminium-Stahl-Seiles 300/69 mm² .

Bei 20- und 110 kV-Leitungen benutzt man Einfachseile. Bei höhere Bemessungsspannungen kann die Randfeldstärke an der Leiteroberfläche von Frei­leitungen grosser als einen kritischen Wert sein und kann Koronaerscheinung eintreten.

Die Koronaerscheinung ist elektrischer Teildurchbruch der Luft, wenn die elektrische Feldstärke einen kritischer Wert an der Oberfläche übersteigt. Für Freileitungen gelten allgemein 16 19 kV/cm.

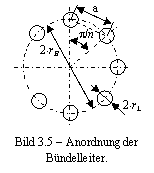
p/n

2 rL

2 rB

Bild 3.5 Anordnung der Bündelleiter.

a

Für die Leitungen mit Bemessungsspannung grosser als 110 kV benutzt man üblich Bündelleiter. Bild 3.5 zeigt die Anordnung der Bündelleiter. Aufteilung des Gesamtquerschittes in mehrere Teilleiter ergibt die Möglichkeit die elektrische Randfeldstärke zu begrenzen.

Die Oberflächen-Randfeldstärke E kann nach folgender Formel berechnet werden

. (3.1)

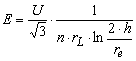
In der Gleichung (3.1) bedeuten: U Betriebsspannung (verkettete Spannung), n Anzahl der Leiter je Bündel, h Leiterhöhe über Boden, r_L Leiterradius, r_e Bündelleiterersatzradius.

Das Bündelleiterersatzradius kann nach folgende Gleichung berechnet werden

, (3.2)

mit

. (3.3)

În der Gleichung (3.3) bedeutet r_B Radius des Bündelumkreises und a Teilleiterabstand (Bild 3.5).

Für 400 kV-Leitungen benutzt man Zweierbündel (2 450/75 mm²), Dreierbündel (3 300/69 mm²) oder Viererbündel (4 240/40 mm²) (Bild 3.6).

Als Beispiel, für eine 400 kV-Leitung mit Viererbündel (4 240/40 mm²) ergibt sich E = 10,67 V/cm (a = 0,4 m ; r_L = 0,01095 m ; r_B = 0,2828 m; r_e = 0,1774 m ; h = 12,4 m)

Zwischen Masten sind die Seile nicht horizontal. Sie haben eine Form (Kettenlinie) die sie durch sein Durchhang f_s definiert lässt (Bild 3.7). Der Durchhang von Seilen wird von den Abspannketten, den Seilgewicht, der zu berücksichttigen Eislast, der Zusatzlast durch Abgänge oder Gegenkontakte für Einsäulentrenner, von der Seilzugkraft, von eingebauten Federn bzw der Federsteifigkeit der Stützpunkte und der Seiltemperatur bestimmt.

Bild 3.6 400 kV-Mast einer Leitung mit einem Stromkreis, Viererbündel und zwei Erdseilen.

Viererbündel

Erdseil

Für die Berechnung von Leitungs­grossen benutzt man normalerweise den mittleren Abstand h_mitt

, (3.4)

mit f_s Durchhang des Seiles; h_min minimaler Abstand gegen Erde; h_A die Höhe der Aufhänge­punkten des Seiles.

Elektrische Feldstärke kann gefährlich für Menschen sein. Deshalb soll man die Feldstärke unter der Leitung rechnen. Sie soll nicht mehr als 10 kV/m sein. Man rechnet die Feldstärke am Boden und an der Höhe von 1,8 m über die Erde (standardiesierte Höhe eines Mensches). Die Feldstärke E_P im Punkt P (Bild 3.8 a)) kann aus folgende Gleichung ermitteln

. (3.5)

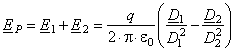
hmin

hmitt

hA

fs

Hängeklemme

Isolatorkette

Bild 3.7 Durchhang eines Seiles.

Wenn der Mensch direkt unter der Leitung steht (Bild 3.8 b)), ergibt sich

. (3.6)

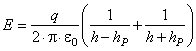
Die elektrische Ladung q kann aus Maxwellsche Gleichung rechnen

, (3.7)

worin U die Spannung zwischen unterspannungstehendem Leiter und Erde ist, a Potentialfaktor

. (3.8)

Elektrische Feldstärke ist am grösste in der Mitte des Spannfeldes. Deshalb nimmt man in der Gleichungen (3.6) und (3.8) h = h_min .

E1

P

E2

EP = E1 + E2

D1

D2

q

q

h

h

a) b) Bild 3.8 Die Berechnung der Feldstärke.

P

h + hP

q

q

h

h

h hP

hP

Als Beispiel, für eine 400 kV-Leitung, in der Mitte des Spannfeldes ergibt sich E_P = 13,51 kV/m (h_P = 1,8 m; h_min = 8 m; r_e = 0,1774 m; e 1/(4 p 10⁹) F/m; U = kV).

3.1.3 Erdseile

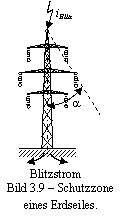
Bild 3.9 Schutzzone eines Erdseiles.

a

iBlitz

Blitzstrom

Schädliche Auswirkungen von Blitzeinschlägen sollen aus technischen und wirtschaftlichen Gründen vollständlich verhindert werden. Freileitungen werden durch Blitzschutzseile (Erdseile) vor direkten Blitz­einschlägen geschützt. Meist kommen St-mehrdrähtige Seile zur Anwendung.

Blitzeinschläge finden in das Erdseil oder in den Mast statt und die unterspannungsstehende Teile der Leitung werden geschützt gegen direkten Blitzeinschläge. Erdseile bestimmen eine Abschirmung der Stromleiter gegen direkten Blitzeinschläge. Die Seile, die in der Schutzzone befindet sich, sind nicht von den Blitzen eingeschlagen. Man kann einen Schutzwinkel kennzeichnen, der kleiner als 30 sein soll (Bild 3.9).

Blitzströme sollen durch niederohmige Erd­widerstände nach Erde geleitet werden.

3.1.4 Isolatoren

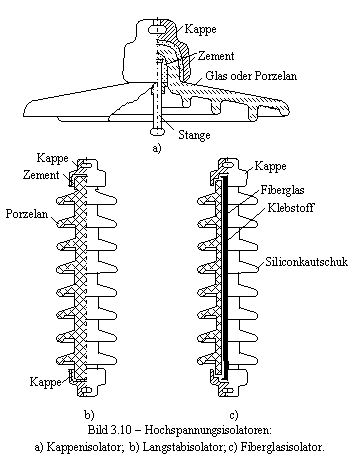
Unterspannungstehenden Leiter müssen gegen geerdeten Mast isoliert werden. Hierzu dienen Isolatoren aus Porzelan, Spezialglas oder Fiberglas. Bild 3.10 a) zeigt einen Kappenisolator aus Spezialglas. Für Isolierung von Phasenleiter von Hochspannungsleitungen verbundet man mehrere Kappenisolatoren in einer Kette. Bei 110 kV-Leitungen benutzt man 7 9 Kappenisolatoren und für die Isolierung einer 400 kV-Leitung benutzt man 22 25 Kappenisolatoren.

b) c) Bild 3.10 Hochspannungsisolatoren: a) Kappenisolator; b) Langstabisolator; c) Fiberglasisolator.

a)

Kappe

Glas oder Porzelan

Stange

Zement

Porzelan

Kappe

Zement

Kappe

Kappe

Fiberglas

Klebstoff

Siliconkautschuk

In Deutschland und in Japan erzeugt man auch Langstabisolatoren aus Porzelan (Bild 3.10 b)). Man benutzt ein Langstabisolator für 110 kV-Leitungen und drei Langstabisolatoren für 400 kV- Freileitungen.

Kappenisolatoren und Langstabisolatoren sind während des Betriebs gleichzeitig mechanisch und elektrisch beansprucht werden.

Heute benutzt man immer mehr Fiberglasisolatoren (Bild 3.10 c). Das Fiberglas soll die mechanische Beanspruchungen standhalten und der Siliconkautschukmantel wird für elektrische Beanspruchungen dimensioniert.

3.2 Ersatzschaltung einer elektrischen Leitung

Die wichtigste Grösse einer elektrischen Leitung, die parallel gegen Erde ist und eine Länge dx hat, sind im Bild 3.11 dargestellt. Dabei sind:

R₀ Wirkwiderstandsbelag [W/km];

L₀ Induktivitätsbelag [H/km];

C₀ Kapazitätsbelag [F/km];

G₀ Konduktanzbelag [1/(W km)].

R0 dx L0 dx

C0 dx

G0 dx

u

i

Bild 3.11 Element der Leitung mit der Länge dx.

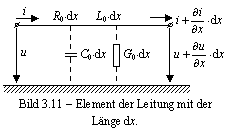
Mit dem ersten Kirchhoffschen Gesetz bekommt man vom Bild 3.11 folgende Gleichungen

. (3.9)

Mit dem zweiten Kirchhoffschen Gesetz bekommt man vom Bild 3.11 folgende Gleichungen

. (3.10)

Aus der Gleichungen (3.9) und (3.10) ergibt sich

( 3.11)

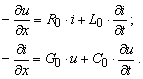
In der komplexen Ebene kann man die Gleichungen (3.11) auf folgende Form schreiben

(3.12)

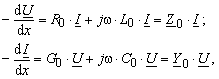
dabei sind Z₀ = R₀ + jw L Impedanzbelag der Leitung; Y₀ = G₀ + jw C Admitanzbelag der Leitung.

Für eine Drehstromleitung (Bild 3.12) kann die Gleichungen (3.12) in der Matrizenschreibweise darstellen.

IA

IB

IC

A B C

UA

UB

UC

Bild 3.12 Drehstromleitung.

;

,

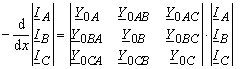
dabei sind:

U_A ; U_B und U_C die Spannungen der Phasen A, B und C gegen Erde;

I_A ; I_B und I_C die Leiterströme in der Phasen A, B und C;

Z_0A ; Z_0B und Z_0C Selbstimpedanzen der Phasen A, B und C;

Z_0AB = Z_0BA ; Z_0BC = Z_0CB und Z_0CA = Z_0AC Kopellimpedanzen zwischen der Phasen A B, BC und CA;

Y_0A ; Y_0B und Y_0C Selbstadmitanzen der Phasen A, B und C;

Y_0AB = Y_0BA ; Y_0BC = Y_0CB und Y_0CA = Y_0AC Kopelladmitanzen zwischen der Phasen A B, BC und CA.

A B C

A B C

l/6

l/3

l/3

l/6

l

Bild 3.13 Verdrillungsplan länger Leitungen.

Längere Leitungen werden verdrillt (Positionswechsel der Leiter an Verdrillmasten) Bild 3.13 um Symmetrie gegen Mast, Erdseil und Erdboden zu erreichen.

Für eine symmetrisierte Leitung kann man die Gleichungen (3.13) auf folgende Form schreiben

;

.

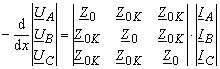
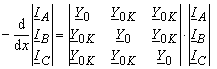
In der Gleichungen (3.14) kann man die Sebstimpedanzen, Koppelimpedanzen, Selbstadmitanzen und Koppeladmitanzen auf folgende Forme schreiben

(3.15)

Durch Differenzieren ergibt sich aus der Gleichungen (3.14)

. (3.16)

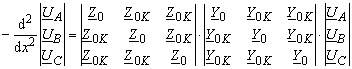
Die Lösung der matrizielen Gleichung (3.16) ist nicht zu bekommen, weil jede Unbekannte von allen anderen Unbekannten abhängt.

Man benutzt eine Transformation in „symmetrischen Komponenten”, bei der induktive und kapazitive Kopplung zwischen der Phasen nicht mehr eintritt (die Impedanz-und Admitanzmatrizen werden nur diagonalen Elementen haben).

3.3 Symmetrische Komponenten

Die Spannungen und die Strömen in der symmetrischen Komponennten­ebene (+, und Null) können auf folgende Form rechnen

(3.17)

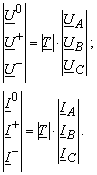
Symmetrierungsmatrix (Transformationsmatrix) ist von der Form

; (3.18)

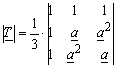
mit

(3.19)

Die Spannungen und die Ströme in der reellen Ebene kann auf folgende Form rechnen

(3.20)

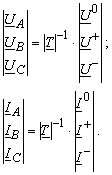
Für die Entsymmetrierungsmatrix gilt es

. (3.21)

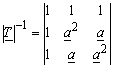
Natürlich

.

Durch Einsetzen der Transformation (3.20) in (3.14) ergibt sich

, (3.22)

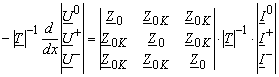
oder

. (3.23)

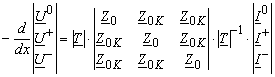
Durch Multiplication der Matrizen bekommt man

.

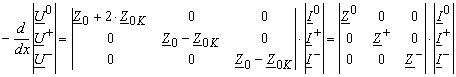
Üblich nennt man Z⁰ = Z₀ + 2 Z_0K als Nullimpedanz; Z⁺ = Z = Z₀ Z_0K als positive Impedanz (gleich mit der negativen Impedanz für elektrischen Leitungen).

Die Impedanzen Z⁰ , Z⁺ und Z lassen sich messtechnisch ermitteln mit den in Bild 3.14 angegebenen Schaltung.

Für die Ermittlung der Nullimpedanz speist man die Drehstromleitung mit dieselber Spannung ein, schliesst man Enden der Leiter kurz und verbindet man zur Erde. Man misst den Strom I_A = I⁰ und die Spannung U_A = U⁰ und man rechnet die Nullimpedanz als Z⁰ = U_A / I_A .

Für die Ermittlung der positiven Impedanz speist man die Drehstrom­leitung mit symmetrischen positiven Spannungen und schliesst man Enden der Leiter kurz. Man misst den Strom I_A = I⁺ und die Spannung U_A = U⁺ und man rechnet positive Impedanz als Z⁺ = U_A / I_A .

Für die Ermittlung der negativen Impedanz speist man die Drehstrom­leitung mit symmetrischen negativen Spannungen und schliesst man Enden der Leiter kurz. Man misst den Strom I_A = I und die Spannung U_A = U und man rechnet negative Impedanz als Z = U_A / I_A .

Wenn die symmetrische Grössen bekannt sind, kann man die Leitung in symmetrischen Komponenten durch die drei einpoligen Ersatzschlatungen im Null , positive und negative Systeme darstellen (Bild 3.15).

G 1~

A B C

U 0 = UA

I 0 = IA

a)

Erde

UA UB UC

UA = UB = UC

3 I 0

3 I 0

G 3~

A B C

U + = UA

I + = IA

b)

Erde

UA

UB = a2 UA

UC = a UA

Bei symmetrischen Speisung (E⁰ = E = 0) aus Drehstromgeneratoren, symmetrisch aufgebauten Betriebsmitteln und symmetrischer Belastung des Drehstromnetzes, die man in normalen, ungestörten Betrieb, sowie bei dreipoligen symmetrieschen Fehler vorausgesetzt kann, reicht es aus, das Drehstromnetz durch die einpolige Ersatzschaltung in der positiven System nachzubilden. Man benötigt Null- und negativen Systeme bei die Berechnung der unsymmetrischen Belastung des Netzes oder der unsymmetrischen Fehler.

IA

IB

IC

A B C

UA

UB

UC

Z0

I 0

Nullsystem

U 0 = Z0 I 0

Z+

I +

Positives System

U + = E Z+ I +

E

Z

I

Negatives System

U = Z I

Bild 3.15 Darstellung einer Drehstromleitung in symmetrischen Komponenten.

G 3~

A B C

U = UA

I = IA

c)

Erde

UA

UC = a2 UA

UB =a UA

Bild 3.14 Messtechnische Ermittlung der symmetrischen Grossen: a) Nullimpedanz; b) Positive Impedanz; c) Negative Impedanz.

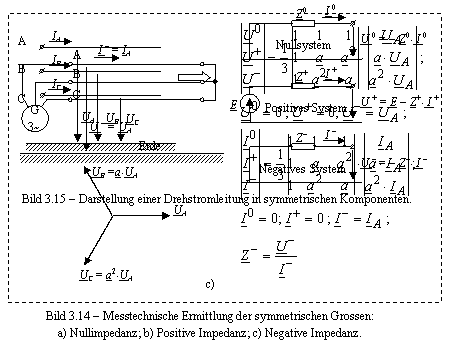
Für die einpolige Ersatzschaltung der Leiter im positiven System werden Impedanzbelag und Kapazitätsbelag aus folgende Gleichungen rechnen :

(3.25)

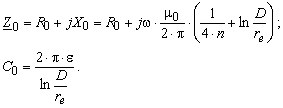
In den Gleichungen (3.25) wird nicht mehr (+) geschrieben aber soll wissen dass die positive Komponenten benutzt sind.

Für den mittleren geometrischen Abstand D, bei einer Drehstromleitung, gilt es (Bild 3.15)

DAB

DCA

A

B

C

Erdseil

DBC

Bild 3.16 Geometrischer Abstand der Stromleiter.

. (3.26)

Für das positiven System kann man Wellenwiderstand Z_W und naturliche Leistung P_nat rechnen

(3.27)

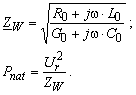
Bei einer verlustlose Leitung (R₀ = 0 und G₀ = 0) ergibt sich der Wellenwiderstand aus folgende Gleichung

. (3.28)

Als Beispiel, für eine 400 kV-Leitung mit Viererbündel (4 240/40 mm², r_e = 0,1774 m ; D_CA = 8,25 m, D_AB = D_BC = 14,5m) ergibt sich

;

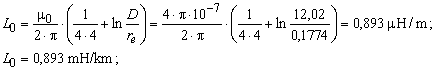
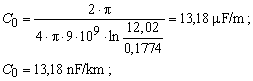
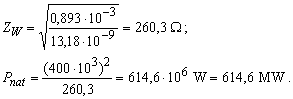
3.4 Leitungsgleichungen

Für einpolige Ersatzschaltung im positiven System kann man die Gleichungen (3.12) benutzen. Durch Differentiation ergibt sich

(3.29)

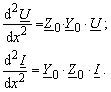
Die Lösung der ersten Differentialgleichung (3.29) ist bekannt

, (3.30)

worin A und B sind Konstanten, die aus Randbedingungen auswerten kann, und

. (3.31)

Aus der ersten Gleichung (3.12) und der Gleichung (3.30) ergibt sich

. (3.32)

Man nennt Z₀/g als Wellenwiderstand Z_W

. (3.33)

Die Gleichungen (3.30) und (3.32) können auf folgende Form geschrieben werden

. (3.34)

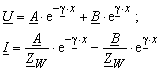
Man nimmt man an, dass die Grösse am Ende der Leitung U_E und I_E bekannt sind. Aus der Gleichungen (3.34) ergibt sich

(3.35)

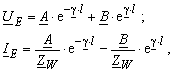
mit l die Leitungslänge.

Konstanten A und B können aus der Gleichungen (3.35) ausgewertet werden

(3.36)

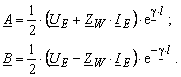
Aus der Gleichungen (3.34) ergibt sich

(3.37)

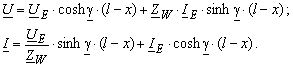
Die Grösse am Anfang der Leitung U_A und I_A kann man für x = 0 aus den Gleichungen (3.37) rechnen

(3.38)

Für eine verlustlose Leitung (R₀ = 0 und G₀ = 0; Z₀ = jw L und Y₀ = jw C ) ergibt sich

(3.39)

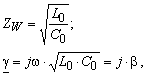
mit

. (3.40)

În der Gleichung (3.40)

(3.41)

ist die Ausbreitungsgeschwindigkeit (Wellengeschwindigkeit) auf eine elektrische Leitung.

Produkt f_l b l nennt man Leitungswinkel.

Für eine verlustlose Leitung kann man die Gleichungen (3.38) auf folgende Form screiben

(3.42)

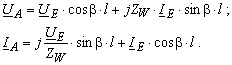
und auch

(3.43)

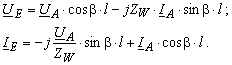
3.4 Bemessung des Leiterquerschnittes

KV iK

A

Aw

Bild 3.17 Wirtschaftlicher Leitungs­­querschnitt.

KV

iK

TK = iK + KV

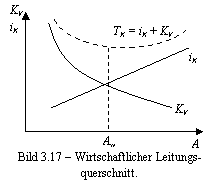Für die Bemessung des Leiterquerschnittes A benutzt man meistens wirtschaftliches Kriterium. Grosse Leiterquerschnitte setzen die Verluste ab, bedingen aber hohe Leitungskosten (Bild 3.17). Die Investitionskosten steigen mit steigendem Querschittt A, während die Verlustkosten K_V mit steigendem Querschittt abnehmen. Es wird somit bei vorgegebener Übertragungsleistung einen wirtschaftlichen Querschitt A_w und eine wirtschaftliche Stromdichte J_w geben, bei der die jährliche Kosten ein Minimum annehmen. Man rechnen heute, für Al/St Seile, mit etwa J_w 0,6 A/mm² .

Die Verlustkostenen K_V [€/Jahr] und auf das Jahr bezogene Investitionskosten i_K [€/Jahr] der Leitung, für eine bestimmte zu übertragende Leistung sollen einen wirtschaftlichen Querschnitt A_w bestimmen. Oder, für eine vorhandene Leitung gibt es eine wirtschaftlice Übertragungs­leistung.

Muss man während der Abschreibungs­dauer der Leitung (35 Jahre) pro Jahr z.B. a = 12% Investitionskosten für Zinsen (Abschreibung oder Amortiesierung) und Wartung bezahlen, so ergibt sich järliche Kosten

i_K a I_K (3.44)

mit I_k Investitionskosten der Leitung.

Die Investitionskosten für den Bau einer Freileitung kann man abhängig von der Spannung und dem Querschnitt abschätzen.

Die Verlustkosten K_V kann man aus folgende Gleichung rechnen

. (3.45)

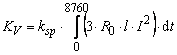
În der Gleichung (3.45) ist R₀ Wirkwiderstandsbelag der Drehstromleitung, l die Leitungslänge, I der Strom (Zeitabhängig), k_sp spezifische Verlustkosten (ungefähr 60 €/MWh), dt Zeitelement.

Für eine bestimmte Querschnittsfläche A der Leitung kann man die Wirtschaftliche Leistung S_w rechnen

, (3.46)

mit U_r Bemessungsspannung der Leitung.

Wichtigste Grössen einer 110 kV – und 400 kV Leitungen sind in der Tabelle 3.1 dargestellt.

Tabelle 3.1

110 kV – und 400 kV Leitungen

	Bemessungspannung der Leitung	kV
	Seilbelegung	mm2
	Bundelleiterersatzradius re	m
	Mittlerer geometrischer Leiterabstand D	m
	Wirkwiderstandsbelag R0	W/km
	Kapazitätsbelag C0	nF/km
	Induktivitätsbelag L0	mH/km
	Wellenwiderstand ZW	W
	Ausbreitungsgeschwindigkeit v	km/s
	Natürliche Leistung Pnat	MW
	Wirtschaftliche Leistung	MVA
	Maste aus Stahl	t/km
	Leiterseile Al/St	t/km

Als Beispiel, wird eine 400 kV Leitung angenommen, die wirtschaftliche Leistung übertragen soll (S = 399 MVA). Für eine Leitung mit der Länge von 100 km ergeben sich folgende Verluste

Man kann den Wirkungsgrad der Leitung rechnen (es wird angenommen dass der Leistungsfaktor der Übertragung l

Die Verlustkosten der Übertragung in einem Jahr sind

€ .

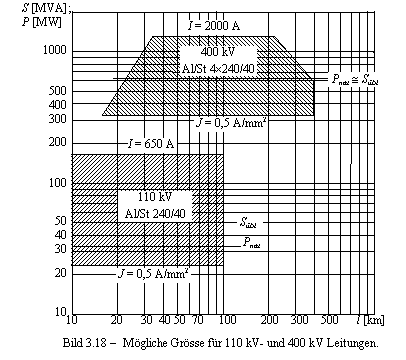
10 20 30 40 50 70 100 200 300 500 l [km] Bild 3.18 Mögliche Grösse für 110 kV- und 400 kV Leitungen.

S [MVA]; P [MW] 1000 500 400 300 200 100 50 40 30 20 10

Pnat

Sübl

J = 0,5 A/mm2

I = 650 A

110 kV Al/St 240/40

J = 0,5 A/mm2

I = 2000 A

400 kV Al/St 4 240/40

Pnat Sübl

Bild 3.18 zeigt die mögliche Grosse bei 110 kV – und 400 kV Leitungen. Es werden die natürliche Leistung und übliche Scheinleistungen eingezeigt. Als obere Grenze für den Leiterstrom (auch für Bundelleiter) wird etwa 2000 A nicht überschreiten, um aufwendige Hochstromkonstruktionen auch in den Schaltanlagen zu vermeiden.

Die Bemessungsspannung einer Freileitung in kV soll möglichst grösser sein als Transportentfernung l in km, anderfalls werden Wirkungrad der Übertragung und die Spannungshaltung zu schlecht.

Der Leitungswinkel f_l soll einen Grenzwert von 0,45 rad nicht überschreiten, anderfalls die Spannungshaltung im Betrieb und die Stabilität bei Störungen kann erschwert sein.

Die Übertragungskosten sollen nicht mehr als 1% der Erzeugungskosten der Leitung sein.

Um die Zuverlässigkeit der Versorgung möglichst hoch zu halten, wendet man nach (n + 1) Kriterim. Bei Ausfall eines Stromkreises, darf die n verbleibende belastende Stromkreise die Versorgung nicht unterbrechen.