Managementul productiei
Firma este entitatea organizatorica si tehnologica cea mai reprezentativa în societatea contemporana. Creativitatea si munca sociala sunt puse în valoare prin intermediul firmelor care indentifica nevoile societatii, antreneaza forta de munca si tehnologii si realizeaza si distribuie catre membrii societatii produsele si serviciile de care este nevoie.
Importanta deosebita a firmelor a determinat aparitia si dezvoltarea unei teorii a firmei care, pâna acum, a fost tratata la nivel microeconomic. Aceasta teorie încearca sa explice si sa previzioneze aparitia si comportamentul firmelor. În acest scop abordeaza o tematica din care fac parte subiecte ca: definirea notiunii de firma, alegerea tipurilor de firma, dimensionarea firmelor, stabilirea profilului firmei, localizarea geografica, determinarea si justificarea investitiei. Cu exceptia definirii notiunii de firma subiectele citate reprezinta repere importante ale studiilor de oportunitate - ca documente de baza necesare pentru înfiintarea firmelor si ale planului de afaceri - în care se actualizeaza valorile previzionate ale reperelor respective, pentru firmele aflate în functiune.
În cele ce urmeaza se vor prezenta succint fiecare din elementele tematice ale teoriei firmei în masura în care se considera ca este necesar pentru întelegerea managementului pe functiuni.
1 Dimensionarea firmelor
Prin dimensionarea unei firme se întelege determinarea mamii ei. Marimea poate fi exprimata, dupa caz, prin volumul de productie sau capacitatea de productie când este vorba de întreprinderi prelucratoare, putere - când este vorba de întreprinderi energetice, suprafata - în cazul firmelor cerealiere. În unele cazuri fimele din industria prelucratoare au marimea exprimata prin numarul de persoane angajate.
Dimensiunea firmelor este o caracteristica tehnico-economica si sociala importanta. De aceasta depind indicatorii economici vitali cum ar fi costurile de productie, profitul, cota de piata a firmei si contributia sa sociala- concretizate prin numarul de locuri de munca asigurate, prin salariile platite si prin influenta asupra gradului de instruire si civilizatie al populatiei din zona în care este amplasata.
Interesul pentru dimensiunea firmelor atinge sfera politicului, politicienii propunându-si în programele lor electorale sa promoveze dezvoltarea economica bazata pe initierea de întreprinderi mici si mijlocii si restructurarea întreprinderilor mari, sau pe internationalizare ce poate favoriza existenta unor întreprinderi mai mari, competitive cu "surorile" lor din alte tari. În viziunea politicienilor se observa uneori inadvertente pe aceasta linie. Procedând prin deductie din comparatii cu alte state, exista riscul sa se preia solutii improprii, asa cum, de exemplu, s-a observat în tarile supuse tranzitiei spre economia de piata, care au tendinta sa imite procesul de creare de întreprinderi în SUA si în alte tari occidentale cu alt nivel economic.
Într-adevar, în SUA firmele mici (atelierele de service, tapiterii, spalatorii chimice, bacanii, saloane de cosmetica, tipografii locale, croitorii, laboratoare, clinici medicale, clinici stomatologice etc.), produc aproximativ 50 % din Produsul Intern Brut (PIB) al tarii si, anual, cele circa 14 milioane de firme mici asigura 80 % din numarul de locuri de munca noi create încât s-a ajuns la formularea sintagmei "small is beautiful" care este si "exportata". Situatia este caracteristica stadiului de dezvoltare a economiei americane. Aceasta a trecut la faza postindustriala - faza serviciilor, iar pentru servicii cele mai potrivite sunt firmele mici, de importanta locala. Ca atare, în tarile care n-au atins acest nivel, se pare ca sintagma "small is beautiful" are sanse sa coexiste cu sintagma "biger is best".
În aceste conditii de pareri diferite, cel mai judicios mod de a opta pentru dimensiune mica, mijlocie, sau mare a întreprinderii este cel bazat pe calcule.
Experienta arata ca problema dimensiunii firmei se pune nu atât pentru firmele complexe, corporatii, holdinguri, concernuri nationale sau/si internationale, pentru care deocamdata nu se concep limite inferioare sau superioare (în cazul acestor firme se pun numai probleme de structura si comunicatii), ci pentru firmele elementare si mai ales pentru uzine sau fabrici individuale. Exemple de astfel de firme pot fi fabricile de bere, întreprinderile de confectii, fabricile de încaltaminte, spalatoriile chimice, întreprinderile industriei alimentare s.a.
Dimensionarea rationala a firmei este impusa
în aceste cazuri în principal de impactul economic al tehnologiei. Orice firma
lucreaza cu o tehnologie care determina costuri diferite în functie
de gradul în care echipamentele, spatiile si suprafetele de
productie sunt ocupate. Chiar si un comerciant detalist care îti
desfasoara operatiile într-un chiosc de aluminiu si
sticla de
Pot fi folosite 2 modele de determinare a marimii firmei:
analiza "punctului de echilibru" dintre cheltuieli si venituri; si
2. modelul "minimizarii costurilor" produsului fabricat.
Modelul analizei "punctului de echilibru" se aplica de obicei pentru firmele de importanta locala, iar modelul minimizarii costului îti are aplicatie pentru firmele de importanta nationala sau/si internationala la care intervin cheltuieli însemnate cu transportul produselor spre consumatori sau utilizatori.
Determinarea marimii convenabile a firmei
folosind analiza "punctului de echilibru" (Break-Even Analysis)
Analiza "punctului de echilibru" este un model care compara încasarile R cu costurile C, exprimate în functie de volumul activitatii X, potrivit reprezentarii grafice din figura 1.
În abscisa graficului din figura 1. se noteaza cu X
volumul productei firmei, în unitati de produse/an. Ordonata masoara
încasarile R, obtinute ca produs între volumul de productie si
pretul unitar p al produselor (R
= pX), si costurile totale C
date de suma dintre costurile fixe - Cf si costurile variabile
cu volumul productiei Cv, adica C = Cf + Cv;
Cv la rândul lor depind de costul variabil pe unitatea de produs v si
volumul productiei X, potrivit formulei Cv = vX. Rezulta costul unitar c al
produsului, c = 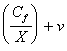 . Volumul critic al productiei, Xcr,
corespunde punctului de echilibru (R = C) al încasarilor R si
costurilor totale C. Pe baza formulelor pentru R si C exprimate mai sus în
functie de X, volumul critic Xcr va fi dat de relatia:
. Volumul critic al productiei, Xcr,
corespunde punctului de echilibru (R = C) al încasarilor R si
costurilor totale C. Pe baza formulelor pentru R si C exprimate mai sus în
functie de X, volumul critic Xcr va fi dat de relatia:
X = 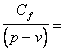 Xcr (2.1.)
Xcr (2.1.)
Cu datele de mai sus poate fi evaluat, de asemenea, profitul p, în lei/an, sub forma,
p = R - C = (p-c)X (2.2.)
Considerând acum un volum de activitate X dat al firmei, prin comparatia cu Xcr calculat cu (2.1.), se pot trage urmatoarele concluzii:
1. X < Xcr p = R - C < 0 (firma va înregistra pierderi);
2. X = Xcr p = R - C = 0 (echilibru între veniturile R si costurile C, respectiv R = C firma nici nu pierde, nici nu câstiga);
3. X > Xcr p = R - C > 0 (firma genereaza profit).
Prima concluzie (1) arata ca
firma care are marimea X mai mica decât cea critica, nu va putea
fi înfiintata pentru ca ar provoca pierderi de la început. Daca
totusi s-ar privi problema în perspectiva si ar exista o
prognoza a evolutiei lui X Xt (t = ![]() ani) de natura
crescatoare, s-ar putea ajunge la o situatie profitabila.
ani) de natura
crescatoare, s-ar putea ajunge la o situatie profitabila.
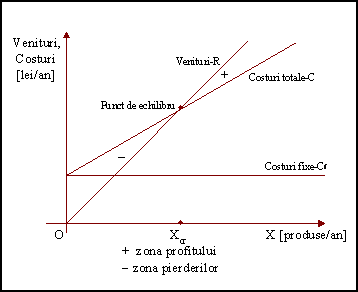
Fig. 1 Modelul grafic al analizei punctului de echilibru
(Break-Even Analysis).
A doua concluzie (2) se suprapune pe definitia metodei analizei punctului de echilibru. Asadar, în conditiile date, firma de dimensiune minima, care nu produce nici piederi nici câstiguri din operatii, are marimea Xcr. Pentru întreprinzatori, Xcr reprezinta un reper orientativ important, care caracterizeaza marimea firmei.
A treia concluzie (3) indica situatia cea mai promitatoare pentru organizarea unei afaceri. Fata de întreprinderea cu marimea critica Xcr, afacerea cu X > Xcr va aduce profit. Dar si în acest caz decizia de angajare în afacere mai necesita tatonari. Este necesar sa se examineze daca profitul p = R - C > 0 este satisfacator. În acest scop se determina rata r a recuperarii capitalului K investit în firma data,
r = ![]() , (2.3.)
, (2.3.)
urmând ca aceasta sa fie comparata cu dobânda d la capitalul depus la banca.
Marimea minima a firmei, acceptabila pentru întreprinzator prin comparatie cu avantajul pe care acesta l-ar avea din depunerea sumei K la banca, va fi cea care satisface conditia
r d (2.4.)
în relatia (2.3.) p reprezinta profitul mediu anual.
La un Xt variabil cu
timpul t =![]() profitul mediu p se poate calcula cu
formula:
profitul mediu p se poate calcula cu
formula:
p =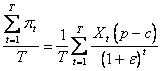 (2.5.)
(2.5.)
În (2.5.) raportul 1/(1+e)t este factorul
de actualizare a banilor, obligatoriu de utilizat în acest caz datorita însumarii
unor profituri pt = Xt (p-c) obtinute
în ani diferiti t = ![]() , deci în conditii de valoare diferita a banilor,
de obicei mai scazuta în viitor fata de prezent; e este rata diminuarii valorii banilor si
poate fi echivalata cu dobânda la credite; p-pret; c-cost unitar.
, deci în conditii de valoare diferita a banilor,
de obicei mai scazuta în viitor fata de prezent; e este rata diminuarii valorii banilor si
poate fi echivalata cu dobânda la credite; p-pret; c-cost unitar.
Daca în formula (2.5.) se admite T = tr, unde tr este timpul de recuperare a capitalului (payback time), se va putea calcula timpul de recuperare tr, verificând relatia:
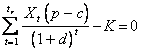 (2.6.)
(2.6.)
Folosind valorile xt (t = ![]() ) se poate gasi o medie a volumului activitatii
firmei de forma:
) se poate gasi o medie a volumului activitatii
firmei de forma:
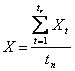 (2.7)
(2.7)
care este considerata dimensiunea caracteristica a firmei prin care se asigura recuperarea capitalului în decursul unui timp tr.
Exemplu de calcul al volumului critic al unei firme
Organizarea unui atelier foto color implica o investitie initiala de 5o mii $ pentru echipamente de laborator, cu durata de serviciu 5 ani, închirierea unui spatiu necesar laboratorului si magazinului de prezentare si desfacere pentru care trebuie platita chiria lunara de 500 $ si o taxa de asigurare de 1000 $/an.
Pretul pietii pentru fotografii color 10x15cm este p = 0,5$, iar costurile variabile (hârtie foto, substante chimice, energie, manopera, ambalaj) reprezinta 0,3 $/fotografie.
Patronul efectueaza aprovizionarea, receptioneaza comenzile clientilor si deserveste magazinul de desfacere în care scop îsi prevede un salariu de 6000 $/an.
Care este volumul critic de activitate al laboratorului foto exprimat în numar de fotografii (10x15)cm, pe an?
Raspuns: Se aplica formula (2.1.) pentru care cheltuielile fixe Cf vor cuprinde: amortizari echipamente (50000$/5 ani = 10.000 $), chiria (500 $/luna x 12 luni = 6000 $); asigurarea (1000 $) si salariul patronului (6000 $),
Cf = 10000 + 6000 + 1000 + 6000 = 23.000 $/an
Stiind ca pretul unei fotografii color este p = 0,5 $ si costul variabil v = 0,3 $, va rezulta volumul critic Xcr al productiei acestui atelier,
Determinarea marimii firmei dupa criteriul
costului minim
În cadrul teoriei manageriale a firmei exista mai multe modele ce optimizeaza output-ul (marimea) firmei cum ar fi modelul maximizarii vânzarilor (W.J. Baumol, 1959), modelul maximizarii cresterii (E.T. Penrose, 1959) si modelul maximizarii utilitatii (O. Williamson, 1964). În cele ce urmeaza se foloseste modelul minimizarii costului ca premiza a maximizarii profitului - obiectiv esential al oricarui model de optimizare a marimii firmelor. Modelul a fost initiat de Bain în 1966.
Se poate dimensiona capacitatea optima a unei uzine, linie de fabricatie sau a unei instalatii complexe care fabrica un singur gen de produse, sau chiar un mix de produse ce pot fi convertite într-un produs conventional.
Explicarea metodei porneste de la modelul grafic al variatiei costurilor în functie de marimea firmei, redat în figura 2.

Fig. 2. Variatia costurilor unitare: C - costul total, C1 - costul de productie si
C2 - costul cu transportul, în functie de volumul X al productiei firmei.
Costul unitar C este o suma a celor 2 costuri C1 si C2 de productie a produsului si de transport la destinatari, adica,
C = C1 + C2 (2.8)
Curba C din figura 2 are un minim caruia îi corespunde , pe abscisa, volumul optim (X*) al productiei. Acesta trebuie calculat. Calculul respectiv necesita explicitarea în functie de (X) a termenilor C1 si C2.
Costul de productie C1 scade cu cresterea volumului de produc]ie X deoarece capacitatea de productie a tehnologiei folosite este utilizata tot mai deplin si efectul "învatarii de a produce" este tot mai mare. Ca atare functia care expliciteaza acest cost în dependenta de X se considera a fi o hiperbola de forma,
În care v,
respectiv a, reprezinta costurile variabile pe unitatea de produs
(manopera directa, materialul de baza, energia tehnologica s.a.),
iar Cf, respectiv b, este cheltuiala anuala
Valorile v si Cf din formula (2.9) se
estimeaza prin metode uzuale de tipul celor fol 636q169g osite în alcatuirea
studiilor de oportunitate pentru asimilari de produse si capacitati
de productie noi, respectiv liste (devize) de cheltuieli si investitii,
bugete de cheltuieli, norme de consumuri de materiale, energie, manopera,
tarife si preturi de catalog. Ele se pot determina, de asemenea, prin
metoda celor mai mici patrate (m.c.m.m.p.), utilizând date statistice Xi
si C1i apartinând unor firme i = ![]() similare, din
similare, din
Costul cu transportul - C2, se stabileste pornind de la relatia,
C2 = DT (2.10)
în care D reprezinta distanta medie, în kilometri, dintre producator si beneficiari, iar T - tariful de transport pe produs si kilometru.
Pentru a face formula (2.10) o functie explicita de X se introduce relatia,
X = S G (2.11)
în care S este aria geografica deservita de firma, iar G - cererea specifica de produse pe unitatea de suprafata. Suprafata S este asimilata ariei cercului pentru ca orice firma deserveste de obicei o arie circulara de raza R. În consecinta (2.11) se poate transcrie sub forma,
X = p R2 G (2.12)
Revenind acum la formula costului transportului (2.10), este necesar a se preciza ca distanta medie într-un cerc are formula:
D = ![]() (2.13)
(2.13)
în consecinta costul cu transportul, explicitat în func]ie de X, va fi:
C2
= ![]() (2.14)
(2.14)
unde
s-a notat Z = ![]() , ca parte
, ca parte
Prin însumarea celor doua costuri C1 si C2 astfel explicitate, se obtine costul total C de forma,
![]() (2.15)
(2.15)
Anularea derivatei acestei functii în raport cu marimea firmei X si substituirea lui Z în formula, permite a se ajunge la dimensiunea optima a firmei,
Aplicatie numerica privind optimizarea marimii X* a
unei firme de calculatoare
Un antreprenor identifica urmatoarele posibilitati de a organiza o firma pentru ansamblare de calculatoare personale (PC) în România (exemplul este ipotetic):
cumpararea unei licente de fabricatie de la o firma consacrata, pentru care urmeaza sa plateasca redevente 50000 $/an;
închirierea unor hale de ansamblare existente, cu o chirie anuala echivalenta cu 10000 $/an;
preluarea în proprietate a unor active de lucru existente în hala închiriata, având o valoare ramasa de 50000 $ si timp de amortizare de 2 ani;
achizitionarea de utilaje noi în valoare de 500000 $, cu durata de amortizare de 5 ani;
salariu si impozite pe salariu pentru conducerea firmei, 50000 $/an;
utilitati pentru functionarea halei de ansamblare (iluminat, caldura, apa calda s.a.) - 50000 $/an;
costurile variabile (componente, materiale, manopera, energie, scule) - 1650 $/PC;
cheltuieli cu ambalarea, manipularea si transportul la beneficiari - 300 $/PC;
se considera ca piata româneasca absoarbe în prezent 50000 PC/an.
Antreprenorul doreste sa afle care ar fi marimea optim\ X* a firmei si daca la un pret p =2000 $, competitiv cu acela practicat de firmele concurente, ar putea obtine un profit pozitiv.
Rezolvare
Se aplica formula marimii optime a firmei (2.16), în care scop este necesar sa se determine:
b - costurile fixe;
G - cererea specifica de calculatoare PC pe km2 în conditiile pietii date;
T - tariful pentru transportul calculatoarelor la clienti.
Costurile fixe b vor fi:
b = 50000$ (licenta) + 10000$ (chirie spatiu industrial) + 50000$/2 ani (amortizare utilaje vechi) + 500000$/5 ani (amortizare utilaje noi) + 50000$ (salariu conducere) + 50000$ (utilitati) = 285000 $/an.
Pentru determinarea cererii specifice se ia în considerare volumul cererii anuale a pietii care se considera egal cu X = 50000 PC- uri si de exemplu, suprafata României S = 237500 kmp [1].
G = ![]() PC/kmp.
PC/kmp.
Tariful de transport T la clienti rezulta din formula (2.10) în care se substituie C2 = 300 $, conform datelor din enuntul problemei,
T = 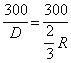 ,
,
unde R este raza cercului; la suprafata României S = 237500 kmp,
raza cercului asociat se obtine din formula,
S = pR2 pR2 R =
Asadar, T = 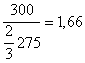 $/PC km.
$/PC km.
Marimile b, G si T calculate mai sus se introduc în formula (2.16) si rezulta
X* = ![]() calculatoare/an
calculatoare/an
La volumul de productie X* = 5300 calculatoare/an, fabrica va realiza cele mai mici costuri de productie si transport si anume:
Cmin = ![]() $
$
în aceste conditii se poate conta pe un profit pozitiv în valoare de,
p = p - Cmin = 2000 - 1805,67 = 194,33 $/produs
Tehnici de prognoza
"Prognoza" este cuvânt de origine greceasca fiind compus din "Pro" (înainte) si "Gnosis" (cunoastere). De aici rezulta ca "prognoza înseamna "cunoastere anticipata". Definitia data prognozei de UNIDO este: o evaluare probabila a evolutiei unor fenomene sau indicatori în decursul unei perioade de timp viitoare denumita orizont de prognoza.
Exista numeroase clasificari ale tipurilor de prognoze dintre care cel mai des sunt citate prognozele sociale, prognozele economice, prognozele financiare, prognozele tehnologice, prognozele meteorologice. La rândul lor metodele si tehnicile de prognoza cele mai cunoscute sunt cele sistematizate în schema din figura 3.
|
|
Întrucât planificarea nu poate fi conceputa fara prognoze, iar diversitatea aplicatiilor acestora este la fel de mare ca si diversitatea fenomenelor si proceselor ce se cer planificate, se impune ca în continuare sa se prezinte succint cele mai importante categorii de tehnici de prognoza mentionate în schema din figura 3. Se începe cu cele mai simple care sunt cele cantitative.
A. Metode cantitative
A1. Metode bazate pe analiza seriilor dinamice
Fenomenele si procesele constituind obiect al prognozei, evolueaza adesea sub forma unor serii de timp. Cele mai simple si mai des utilizate metode bazate pe analiza seriilor de timp sunt metodele mediei mobile si ajustarii exponentiale.
Metoda mediei mobile
Metoda mediei mobile determina prognoza pentru o perioada de timp viitoare (ora, zi, saptamânâ, luna, trimestru, an) prin medierea datelor din ultimele n perioade de timp potrivit formulei,
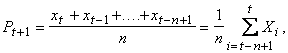 (7.10)
(7.10)
în care:
![]() - reprezinta
valoarea prognozata pentru perioada (t+1);
- reprezinta
valoarea prognozata pentru perioada (t+1);
![]() - valoarea
realizata în perioada t.
- valoarea
realizata în perioada t.
În tabelul 1 se prezinta informatii asupra vânzarii de computere personale (PC) de catre o firma specializata în distributia tehnicii de calcul.
|
Anul |
Trimestrul |
Numarul perioadei, ti |
Vânzari (103PC/an) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Datele din tabelul
1 sunt folosite ca exemplu pentru ilustrarea variatiei mediei mobile si
a prognozarii vânzarilor pentru perioda (t+1). Astfel, daca se adopta n=4 , atunci prognoza ![]() pentru primul
trimestru al anului 1998 va fi
pentru primul
trimestru al anului 1998 va fi ![]()
În graficul din figura 4 se prezinta comparativ variatia reala a vânzarilor de computere, conform datelor din ultima coloana a tabelului si prognozele vânzarilor calculate cu formula (7.10) în care ordinul mediei mobile este n=4.
Se observa masura în care media mobila urmareste evolutia datelor reale. Evident, adoptând un alt ordin al mediei mobile, se poate ajunge la o corespondenta mai apropiata sau mai departata a curbei prognozei fata de curba evolutiei datelor reale. Cu calculatorul electronic se pot testa diversele ordine ale mediei si se poate alege ordinul (n) care asigura abaterea minima a prognozei fata de realitate.
Eroarea poate fi apreciata pe baza diferentelor dintre realitate si prognoza folosind formula erorii medii
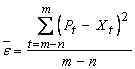 (7.11)
(7.11)
în care ![]() sunt valorile
prognozate pentru perioadele
sunt valorile
prognozate pentru perioadele ![]()
![]() - valorile reale
disponibile;
- valorile reale
disponibile;
m - numarul de valori ale seriei de timp disponibile (de ex. în tabelul 1., m = 16)
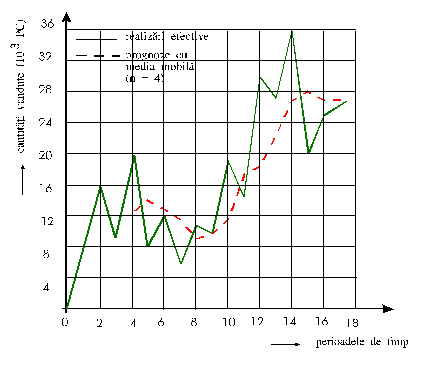
Fig. 4. Vânzari efective si prognozele acestora determinate cu
media mobila de ordin n = 4.
Metoda ajustarii exponentiale
Aceasta
metoda se bazeaza pe ipoteza ca prognoza pentru o perioada
viitoare ![]() trebuie sa contina
2 componente: valoarea reala a perioadei trecute
trebuie sa contina
2 componente: valoarea reala a perioadei trecute ![]() si valoarea
prognozata pentru perioada trecuta
si valoarea
prognozata pentru perioada trecuta ![]() (trendul) luate cu
ponderile
(trendul) luate cu
ponderile ![]() si respectiv
si respectiv ![]() , potrivit formulei:
, potrivit formulei:
Ponderile ![]() si
si ![]() denumite operatori de
ajustare au semnificatia unei atitudini fata de prezent si
trecut. Când
denumite operatori de
ajustare au semnificatia unei atitudini fata de prezent si
trecut. Când ![]() , rezulta
, rezulta ![]() . Înseamna ca în acest caz se pune accentul numai
pe trecut. Când
. Înseamna ca în acest caz se pune accentul numai
pe trecut. Când ![]() , rezulta
, rezulta ![]() ; se neglijeaza total tendinta din trecutul
fenomenului, contând numai realizarile prezentului. Folosita în
meteorologie, de exemplu, aceasta atitudine conduce la prognoza potrivit careia
" cel mai probabil este ca ziua de mâine sa fie ca azi". Denumirea de
ajustare exponentiala se explica în felul urmator. Fie
; se neglijeaza total tendinta din trecutul
fenomenului, contând numai realizarile prezentului. Folosita în
meteorologie, de exemplu, aceasta atitudine conduce la prognoza potrivit careia
" cel mai probabil este ca ziua de mâine sa fie ca azi". Denumirea de
ajustare exponentiala se explica în felul urmator. Fie ![]() prognoza pentru
perioada t data de relatia,
prognoza pentru
perioada t data de relatia,
![]() (7.13)
(7.13)
Se înlocuieste
![]() astfel exprimat în
(7.12) si rezulta,
astfel exprimat în
(7.12) si rezulta,
![]() (7.14)
(7.14)
Se constata astfel ca în evaluarea prognozei prin metoda ajustarii exponentiale, valorile trecutului nu au aceeasi pondere ca acelea ale prezentului, ci descresc exponential.
Prin aceasta
metoda se poate interveni în vederea atenuarii criticilor la adresa
prognozelor prin extrapolare, critici care imputa acestor metode neajunsul
de a proiecta viitorul prin copierea trecutului perimat. Asa cum s-a mentionat
mai sus, adoptând o valoare ![]() mai mica, se
imprima o importanta mai mica trecutului si
complimentar - una mai mare prezentului si viceversa.
mai mica, se
imprima o importanta mai mica trecutului si
complimentar - una mai mare prezentului si viceversa.
Formula (7.15) arata ca
prognoza ![]() se obtine prin
însumarea prognozei
se obtine prin
însumarea prognozei ![]() , aferenta perioadei prezente, cu eroarea de prognoza
, aferenta perioadei prezente, cu eroarea de prognoza
![]() luata de
luata de ![]() ori. Aceasta
constatare prezinta o mare importanta practica. Daca
seria de timp este una puternic oscilanta si contine o substantiala
variabilitate aleatoare înseamna ca pentru ca prognoza sa fie
cât mai apropiata de fapte este necesar a fi folosita o pondere mica
ori. Aceasta
constatare prezinta o mare importanta practica. Daca
seria de timp este una puternic oscilanta si contine o substantiala
variabilitate aleatoare înseamna ca pentru ca prognoza sa fie
cât mai apropiata de fapte este necesar a fi folosita o pondere mica![]() . Dimpotriva, pentru serii stabile, cu variabilitate
aleatoare redusa, constantele de ajustare
. Dimpotriva, pentru serii stabile, cu variabilitate
aleatoare redusa, constantele de ajustare ![]() mai mari sunt
preferate deoarece au avantajul ca în caz de producere a unor erori de
prognoza însemnate pot ajusta fara întârziere prognoza,
conferind astfel acesteia o capacitate de reactie rapida la schimbarile
de conditii.
mai mari sunt
preferate deoarece au avantajul ca în caz de producere a unor erori de
prognoza însemnate pot ajusta fara întârziere prognoza,
conferind astfel acesteia o capacitate de reactie rapida la schimbarile
de conditii.
Cele 2 metode de prognoza prezentate mai sus sunt intersanjabile ca destinatie: ambele sunt metode de prognoza pe termen scurt. În ce mod se ajunge a se apela la una sau alta dintre acestea, se arata în aplicatia ce urmeaza:
Exemplu numeric de aplicare a ajustarii exponentiale si de alegere a metodei optime pentru prognoza pe termen scurt (comparatie între ajustare si media mobila).
În tabelul 3 se prezinta valorile deverului real si prognozele aferente pentru o statie de benzina pe o perioada de 15 saptamâni.
Prognozele ![]() s-au calculat cu
formulele mediei mobile (7.10) si ajustarii exponentiale (7.12).
Ajustarea exponentiala s-a efectuat în doua variante ale
operatorului
s-au calculat cu
formulele mediei mobile (7.10) si ajustarii exponentiale (7.12).
Ajustarea exponentiala s-a efectuat în doua variante ale
operatorului ![]() si anume
si anume ![]() si
si ![]() . În figura 7.4 sunt reprezentate curbele variatiei
valorilor deverului real comparativ cu prognozele vânzarilor în cele 3
alternative de evaluare a prognozelor.
. În figura 7.4 sunt reprezentate curbele variatiei
valorilor deverului real comparativ cu prognozele vânzarilor în cele 3
alternative de evaluare a prognozelor.
Se poate observa ca prognozele se înscriu în apropierea valorilor reale ale deverului, existând unele diferente care constituie erorile prognozei.
Sarcina analistului planificator este sa identifice modelul de prognoza optim.
Vânzarile de benzina si prognozele saptamânale, exprimate în 103 litri, la o statie "PETROM"
|
S\pt\mâna |
Vânz\ri |
Prognoza |
||
|
t |
|
Ajustare exponen]ial\
|
Ajustare exponen]ial\
|
Media mobil\ (n=4) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Pentru alegerea metodei si alternativei de prognoza optime, analistul se poate ghida dupa criteriul erorii minime.
În cazul de fata
erorile de prognoza ![]() sunt prezentate
asociat fiecarei alternative de prognoza (i) în tabelul.4.
sunt prezentate
asociat fiecarei alternative de prognoza (i) în tabelul.4.
Erorile de prognoza în cazul a 3 alternative de calcul al
prognozelor pentru statia de benzina
|
Cu ajutorul erorilor din tabelul 7.4. se calculeaza eroarea medie absoluta (deviatia medie absoluta - DMA), iar valorile acesteia s-au notat pe graficul din figura 7.4.
Fig. 7.4. Deverul saptamânal
al unei statii "PETROM" si prognozele vânzarilor prin ajustari
cu Rezulta ca
dupa criteriul erorii de prognoza minime, cea mai buna dintre
cele 3 alternative de calcul a prognozei, în acest caz concret, este ajustarea
exponentiala cu Asadar, pentru cazul de fata alegerea metodei optime de prognoza necesita rationamente suplimentare. Spre a efectua aceste rationamente se precizeaza ca erorile cu (+) semnifica o subaprovizionare fata de cererea reala, iar cele cu (-), o crestere inutila a stocului. Trebuie calculate, prin urmare, pierderile cauzate statiei de fiecare din cele 3 alternative de prognoza. În ipoteza admiterii unui pret de 750 lei/litrul de benzina, a unei rentabilitati a statiei de benzina de 5% fata de vânzari si a dobânzii de 90% pentru creditarea stocurilor , pierderile asociate celor 3 alternative de prognoza sunt sistematizate în tabelul 7.5. În vederea evaluarii pierderilor s-au însumat, pe baza tabelului 7.4, erorilor cu (+) si cele cu (-) la fiecare alternativa de prognoza, rezultând: pentru ajustarea cu pentru ajustarea cu a=0,3 , erori cu (+) 41,7 tone, erori cu (-) 54,3 tone; pentru media mobil\ cu n=4, erori cu (+) 32,2 tone, erori cu (-), 49,85 tone. În urma calculelor economice prin care se evidentiaza pierderile datorate erorilor de prognoza, rezulta ca alternativa de prognoza cea mai buna este cea care foloseste media mobila cu n=4. Tabelul 7.5 Pierderile datorate erorilor de prognoza pentru o statie de benzina în decursul a 11 sapamâni în cazul a 3 alternative de prognoza
Se pune întrebarea daca o prognoza cum este cea optima realizata în cazul de mai sus prin folosirea mediei mobile cu n=4, pentru care pierderile determinate de eroarea de prognoza costa firma 1.890.540,9 lei pe 11 luni, este sau nu eficienta. Spre a raspunde la aceasta întrebare, se cere a se cunoaste modul în care se desfasoara aprovizionarea reala a firmei. Graficul evolutiei deverului real de benzina al statiei reprezentat în figura 7.4., sugereaza ca spre a fi posibila o asemenea evolutie, aprovizionarea s-a facut în mod acoperitor fata de vârfurile deverului. Înseamna ca firma a suportat cheltuieli substantiale cu plata dobânzilor pentru creditarea stocului suplimentar. Spre a avea comparabilitate cu situatia economica folosita în rationamentele referitoare la identificarea metodei optime de prognoza, urmeaza a evalua pierderea cu stocarea înregistrata de statie în acelasi interval de timp, de 11 saptamâni. Pe graficul din figura 7.4 se observa ca spre a face fata vârfurilor de consum al clientilor, firma s-a aprovizionat cu o cantitatea maxima de 87.000 litri, iar diferentele fata de consumul clientilor au reprezentat:
Pierderea datorata stocarii acestui plus de aprovizionare fata de cererea reala este,
De aici este evident ca oricare din cele 3 alternative de prognoza asigura un efect pozitiv pentru firma. Efectul maxim este asigurat de aplicarea prognozei prin metoda mediei mobile cu n=4. Efectul economic E adus firmei prin aprovizionarea saptamânala cu cantitatile prognozate prin metoda mediei mobile reprezinta: Cantitatea prognozata pentru saptamâna 16, cu media mobila de ordin n=4, va fi: Prognoze prin extrapolarea tendintei Metodele mediei mobile si ajustarii exponentiale sunt aplicabile în prognozele pe termen scurt, de pe o zi pe alta, de pe o luna pe alta, de pe un trimestru pe altul. Ca atare ele sunt utile în mod deosebit pentru elaborarea planurilor de actiune si la controlul îndeplinirii planurilor curente. în care Tipul de functie matematica asociat seriei se identifica prin metoda diferentelor finite dupa cum urmeaza: 1) Daca
momentele Pentru
exemplificarea modulului de calcul al diferentelor finite se considera
o serie de 4 valori 2) Daca
momentele Exemplu: Fie
seria Diferentele finite de ordinul 1 vor fi: în acest caz, functia ce trebuie extrapolata va fi polinomul de ordinul 2, 3) Daca
diferentele finite calculate succesiv: 4) Daca În oricare din
cazurile 1), 2), [i 4) de mai sus parametrii functiei se pot stabili prin
metoda celor mai mici patrate (mcmmp). Potrivit cu aceasta se scrie o functie
W a celor mai mici patrate ale diferentelor dintre valorile
statistice unde Pentru a îndeplini conditia de minim, derivatele acestei functii în raport cu a si b se anuleaza astfel: Rezulta sistemul de ecuatii normale:
În cazul functiei exponentiale (7.20) sistemul de ecuatii normale va rezulta dupa ce se face linearizarea prin logaritmare, Sistemul de ecuatii normale asociat acestei noi exprimari va fi Aplicatie numerica. Prognoza prin extrapolarea tendintei înzestrarii populatiei României cu autoturisme. Din anuarul statistic rezulta ca înzestrarea populatiei cu autoturisme consemnata din 5 în 5 ani este cea redata în tabelul 7.6. (valori rotunjite, pentru simplificarea calculelor). Tabelul 7.6 Înzestrarea populatiei cu autoturisme în perioada 1980-1995
Se cere: a) Sa se stabileasca functia evolutiei înzestrarii cu autoturisme; b) Sa se determine prognoza înzestrarii populatiei cu autoturisme pentru anul 2000; c) Sa se estimeze volumul de productie al industriei de automobile destinate pentru piata interna, în anul 2000, daca se admite ca numai jumatate din automobilele cu care este înzestrata populatia în 1995 vor fi apte sa functioneze în anul 2000. R\spuns: a). Se calculeaza diferentele finite de ordinul 1 O serie de timp având diferente finite de ordinul 1 constante, se rezolva printr-o dreapta de forma celei din formula (7.17). Se calculeaza parametri a si b ai dreptei, folosind sistemul ecuatiilor normale (7.22). Din examinarea structurii sistemului de ecuatii normale rezulta ca este necesar sa se alcatuiasca tabelul ajutator 7.7. Tabelul 7.7Pregairea datelor numerice necesare rezolvarii sistemului (7.22)
Se înlocuiesc datele situate pe ultima liniei a tabelului, în sistemul (7.22):
Se rezolva acest sistem în raport cu a si b, rezultând: Formula dreptei pentru prognoza înzestrarii populatiei cu automobile va fi, b) Prognoza
înzestrarii populatiei cu autoturisme în anul 2000, caruia îi
corespunde c) Pentru a
dispune de 70 autoturisme la 1000 locuitori în anul 2000, în conditiile în
care numai jumatate din numarul de autoturisme existente la 1000
locuitori în 1995, adica Metoda seriilor de timp decompozabile Din prezentarea metodei extrapolarii trendului s-a vazut ca atunci când seria de timp nu are diferente finite constante, ea comporta pe lânga trend si alte componente. Metoda seriilor de timp decompozabile preconizeaza existenta a 4 componente ce însotesc o serie de timp de acest fel: 1) Trendul (T); 2) Variatia sezoniera (S); 3) O variatie ciclica (C); Variatia aleatoare (R).
Fig. 7.6. Componentele unei serii de timp În figura 7.5
sunt reprezentate grafic, distinct, 3 dintre aceste componente: trendul (T), ciclul
(C) si variatia sezoniera (S). Economistii au ajuns la
concluzia ca aceste componente pot exprima prognoza Trendul ( Componenta ciclica ( Componenta sezoniera (St) se manifesta ca urmare a influentelor sezonale din timpul anului. Are oscilatie mai frecventa decât componenta ciclica. Uneori variatia sezoniera cantitativa coincide cu sezoanele ca, de exemplu, în cazul consumului casnic de energie electrica - mai mare iarna comparativ cu vara. Alteori, variatia sezoniera se manifesta în avans cu o etapa (sezon) ca de exemplu, productia de obiecte care constituie cadouri de iarna, accentuata în sezonul de toamna spre a face fata cerintei de cadouri în iarna. Componenta aleatoare ( Ca metodologie de evaluare, prognoza pe baza seriilor decompozabile, comporta doua tipuri de valuari: trendul ( componentele ciclica, sezoniera si aleatoare se determina prin metodele indexarii, asa cum se va explica pe un exemplu metodologic în continuare. În tabelul 7.8 sunt înregistrate valorile seriei vânzarilor de difuzoare stereofonice de catre firma "Stereoton" pe parcursul a 5 ani, divizati pe trimestre.Tabelul 7.8 Vânzarile de difuzoare stereo ale firmei "Stereoton" pe parcursul a 5 ani, în 103 buc. / trimestru
Se cere sa se prognozeze vânzarile în anul 6, cu divizare pe trimestre Raspuns Tipul functiei
trendului ( Dispunând de datele din tabelul 7.8 si aplicând mcmmp, se ajunge la sistemul de ecuatii normale asociat functiei (7.27),
De aici rezulta
parametrii dreptei:
Fig. 7.6. Graficul variatiei vânzarilor de difuzoare stereo pe 5 ani la firma
"Stereoton" si reprezentarea tendintei acestor vânzari
- Calculul indexului componentei ciclice Ct. Pe graficul din figura 7.6 se observa ca în acest exemplu numeric exista o variatie ciclica quasievidenta în jurul tendintei. Indexul cu ajutorul caruia urmeaza a fi luata în calcul variatia ciclica se va exprima ca proportie în raport cu tendinta. În acest scop se utilizeaza media mobila de ordinul 4 menita sa elimine influentele sezoniere care, dupa cum arata curba vânzarilor din figura, sunt si ele prezente în acest caz. Ordinul 4 al mediei este, asadar, dictat de variatiile trimestriale. Media pe 4 trimestre netezeste iregularitatile sezoniere. De asemenea, este necesar a preciza ca pentru a asigura variatia cicloidala se face un calcul suplimentar care introduce în procesul constructiei cicloidei asa numitele medii centrate (MMC). Ele se calculeaza cu formula,
în care În tabelul 7.9
se prezinta valorile indecsilor În figura 7.7 este
reprezentata curba cicloidala a indecsilor ( Fig. 7.7. Ciclul vânzarilor firmei "Stereoton" si extrapolarea lui în viitor Tabelul 7.9 Calculul indecsilor ciclului, cu aplicatie la vânzarile firmei "Stereoton"
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||