MODELE SI METODE DE CALCUL IN PROIECTAREA CONSTRUCTIILOR

MODELE SI METODE DE CALCUL ÎN PROIECTAREA CONSTRUCŢIILOR

INTRODUCERE

În limbajul uzual prin constructie se întelege o cladire executata din zidarie, lemn, metal, beton, etc., pe baza unui proiect, care serveste la adapostirea oamenilor, animalelor, obiectelor, etc. (1 DEX). Terminologia tehnica defineste constructia ca structura sau sistem fizic, aflat in permanenta actiune cu mediul inconjurator. Intrarile in sistem sunt actiunile exercitate de mediu asupra structurii, iar raspunsul structurii la aceste actiuni constituie iesirile din sistem .

Orice constructie are un schelet sau o structura de rezistenta, alcatuita din elemente simple numite elemente de constructii ( bare, placi, blocuri).

Având în vedere elementele care intra în componenta structurilor de rezistenta, acestea pot fi grupate în:

structuri din bare (articulate sau legate rigid în noduri);

structuri alcatuite din pereti structurali (de zidarie portanta, din beton turnat monolit sau în panouri prefabricate, din materiale compozite, etc.);

structuri mixte, alcatuite din bare si pereti structurali.

Proiectarea unei constructii este un proces complex în care ponderea cea mai mare o are analiza si proiectarea structurii de rezistenta ("structural analysis and design"). Prin aceasta proiectare se urmareste realizarea unei structuri care sa satisfaca exigentele esentiale functionale si economice, cu asigurarea cerintelor de rezistenta, rigiditate, stabilitate si durabilitate, deci a sigurantei in exploatare.

MODELAREA FIZICĂ A STRUCTURII, REAZEMELOR sI ACŢIUNILOR

Avand în vedere complexitatea de alcatuire a strucurilor de rezistenta, a legaturilor interioare si exterioare (rezemarilor), precum si complexitatea încarcarilor si a comportarii materialelor constitutive, analiza si proiectarea structurala se face pe un model structural simplificat (idealizat). Aceasta presupune schematizarea constructiei si a elementelor de constructii componente ca forma, dimensiuni geometrice, materiale constitutive si chiar neglijând unele elemente neportante (cu rol de compartimentare, de izolare higrotermica si acustica, decorativ etc.).

Similar, legaturile exterioare ale structurii (reazemele) si cele interioare, dintre elemente, se idealizeaza reducându-se la trei tipuri fundamentale: reazem simplu, articulatie, încastrare. Reazemele se diferentiaza în cazul plan, respectiv spatial, prin numarul si directia gradelor de libertate blocate (total în cazul reazemelor fixe, partial în cazul reazemelor elastice).

Actiunile (încarcarile) pe care trebuie sa le preia o constructie în decursul vietii sale sunt foarte variate ca natura, provenienta si mod de manifestare. Ele se schematizeaza si se reduc la forte si momente concentrate, respectiv distribuite, deplasari impuse, variatii de temperatura. Clasificarea actiunilor se poate face dupa mai multe criterii, cum ar fi (RM1):

dupa criteriul frecventei de aparitie la anumite intensitati (actiuni permanente - P, actiuni temporare - T, actiuni exceptionale - E);

dupa locul de aplicare (forte masice sau de volum si forte de suprafata - active sau reactive);

dupa modul de actiune în timp (actiuni statice, respectiv dinamice);

dupa pozitia actiunilor în timp (actiuni fixe, respectiv mobile).

În conceptul sistemic actiunile constituie modelul de încarcare al structurii, definit prin parametrii de intrare cunoscuti (P).

Modelul structural caruia i se ataseaza modelul de încarcare formeaza modelul structural de calcul.

MODELAREA COMPORTĂRII MATERIALELOR

Comportarea structurii de rezistenta a oricarei constructii este influentata semnificativ de materialele constitutive. Caracteristicile fizico-mecanice si elastice ale materialelor se obtin pe cale experimentala, prin încercari pe probe standardizate, în urma carora se obtin curbe caracteristice specifice fiecarui material. Diversitatea de curbe caracteristice ale materialelor frecvent utilizate în constructii a impus schematizarea lor prin folosirea unor modele de deformare (reologice) simple, corespunzatoare celor trei tipuri de deformatii elementare: elastice, plastice, vascoase (JUD). Din acest punct de vedere exista trei categorii de materiale, dupa cum urmeaza:

- materiale cu comportare elastica liniara, schematizeaza printr-un resort (modelul fundamental Hooke), având curba carasteristica din fig. 1.1.a; comportarea elastica liniara este descrisa matematic în cazul unei solicitari uniaxiale de legea lui Hooke:

σ = Eε (1.1)

unde E - constanta elastica a resortului este modulul de elasticitate longitudinal al materialului. La solicitari bi sau triaxiale legatura σ - ε este precizata de legea generalizata a lui Hooke;

- materiale cu comportare plastica, schematizeaza printr-o patina (modelul fundamental Saint-Venant), curba caracteristica fiind cea din fig. 1.1.b; ecuatia de stare (reologica) la solicitare uniaxiala este

σ = σ_c (1.2)

unde σ_c - valoarea tensiunii la care este invinsa frecarea dintre patine (limita de curgere a materialului); la solicitari bi sau triaxiale se utilizeaza criterii (teorii) de curgere;

- materiale cu comportare vascoasa, la care viteza de deformare variaza liniar sau neliniar în raport cu tensiunea (beton, materiale plastice, etc.); modelul de deformare este schematizat printr-un piston (modelul fundamental Newton- fig. 1.1.c), iar ecuatia de stare care descrie comportarea vascoasa este

σ = µέ (1.3)

unde µ - caracteristica pistonului ( coeficientul de vascozitate al materialului ), έ - viteza de deformare.

Curbele caracteristice ale multor materiale cu comportare elastica sau vascoasa sunt neliniare sau prezinta portiuni neliniare. Un material cu comportare elastica pronuntat neliniara este cauciucul (fig. 1.1d).

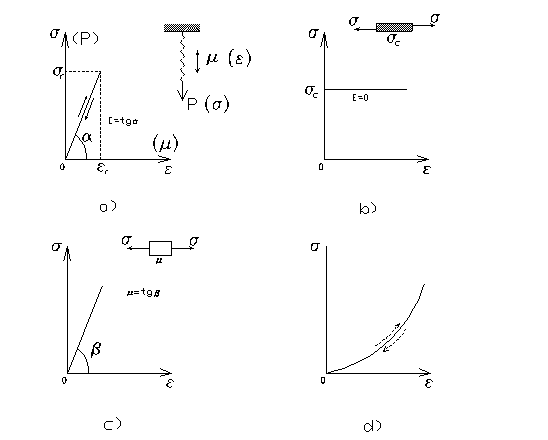
Fig. 1.1

Materialul constitutiv al unei constructii poate avea, la un moment dat, doua sau chiar toate cele trei tipuri de deformatii elementare, desigur în procente diferite, functie de material, gradul de solicitare, temperatura, etc.

De aceea a fost necesara crearea de modele reologice compuse, obtinute prin legarea în serie sau an paralel a modelelor fundamentale, ecuatiile de stare obtinându-se similar, pe baza conditiilor de echilibru si de compatibilitate geometrica a modelului compus.

Un astfel de model, prin care se aproximeaza comportarea elasto-plastica a otelului, este obtinut prin legarea în serie a unui resort cu o patina. Modelul elastic-perfect plastic obtinut

conduce la curba caracteristica din figura 1.2 a, numita si curba Prandtl. Matematic, comportarea

acestui model se traduce printr-o ecuatie de stare discontinua;

σ = Eε - pentru ε < ε_e ( < σ_c ) (1.4)

= σ_c - pentru ε > ε_e

unde ε_e - deformatia specifica la limita de elasticitate a materialului.

Curba caracteristica a otelului (fig. 1.2 b) poate fi aproximata si mai bine printr-un model elasto-plastic cu consolidare (fig. 1.2 c).

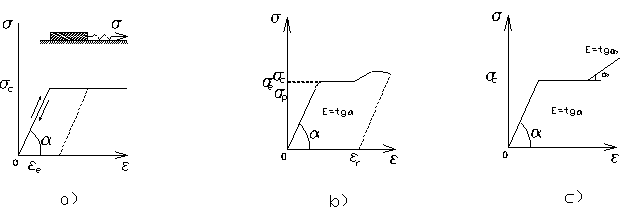
Fig. 1.2

În literatura de specialitate se întâlnesc si alte modele complexe de comportare a diverselor materiale, carora le corespund curbe caracteristice specifice (modelul biliniar, modelul neliniar elasto-plastic, curba Ramberg-Osgood, etc.).

Comportarea mecanica a materialelor de constructii care, asa cum s-a vazut, este de natura experimentala, se exprima mai general prin ecuatii reologice de forma:

f(σ,σ,..ε,έ,..,t,T) = 0 (1.5)

adica o functie de tensiuni, deformatii specifice si derivatele lor în raport cu timpul, precum si de timpul (t) si temperatura (T). În spatiul σ- ε- t ecuatia (1.5) reprezinta o suprafata caracteristica având ca proiectii în fiecare plan curba caracteristica σ- ε si curba de fluaj sau curgere lenta ε-t

Modelul structural obtinut prin schematizarea constructiei, la care se ataseaza modelele simplificate ale legaturilor, încarcarilor si ale comportarii materialelor constitutive formeaza modelul fizic al structurii reale.

MODELAREA EXPERIMENTALĂ

La unele constructii unicat sau speciale, de mare importanta, ce trebuie proiectate sau sunt deja executate, dar a caror capacitate de a fi utilizate în continuare trebuie expertizata, se impune efectuarea unor cercetari experimentale pe modelele fizice structurale. Daca este posibil, aceste modele pot fi identice cu structura reala, caz în care modelul experimental este un prototip. În caz contrar, modelul experimental se realizeaza la o scara redusa, pe baza legilor de similitudine cu structura reala. Aceste legi se refera la stabilirea dimensiunilor geometrice si a modulului de rezemare, la alegerea materialului constitutive si a schemei de încarcare a modelului.

Modelul experimental se echipeaza cu aparatura si dispozitive de actionare, de înregistrare, masurare si prelucrare a unor parametri de raspuns (deplasari, deformatii, acceleratii, etc.).

Modelul fizic este încercat pe baza unui program experimental,obtinându-se valori ale parametrilor de raspuns, fie direct prin masurare, fie dupa unele prelucrari, de obicei automate, bazate pe teoria similitudinii.

Rezultatele obtinute se folosesc la stabilirea modului de comportare a structurii reale, la confruntarea cu rezultatele teoretice obtinute prin analiza modelului structural de calcul si, pe aceste baze la luarea unor decizii de îmbunatatire a modelului structural de calcul si a proiectarii structurii reale.

În anumite situatii, costul mare si durata îndelungata a unui program experimental pot fi evitate prin înlocuirea cu un program de simulare numerica a experimentarilor.

MODELAREA MATEMATICĂ A COMPORTĂRII STRUCTURILOR sI DETERMINAREA RĂSPUNSULUI

Consideratii introductive

Comportarea sub actiuni a oricarei structuri de rezistenta (reale sau model de calcul) este un proces a carui evaluare se face printr-o serie de parametri fizico-mecanici (variabile), X(x,y,z,t), care sunt functii continue de coordonatele spatiale si de timp (procesul este stationar daca t=0, respectiv nestationar daca t≠0). Unele dintre aceste variabile, q, care constituie parametrii de intrare, în sistem si parametrii proprii ai sistemului, pot fi cunoscute sau stabilite apriori: actiunile (P), unele dimensiuni geometrice (L), caracteristicile fizico-mecanice ale materialului (E), conditiile la limita. Restul de u variabile, reprezentând parametrii de raspuns ai structurii, constituie necunoscutele problemei: deplasari, eforturi (tensiuni), temperaturi, viteze, etc. Prin urmare, parametrii de raspuns sau de iesire ai structurii pot fi reprezentati prin functii, în general continue, dependente de parametrii de intrare si de parametrii proprii ai sistemului:

Y=Y(x,y,z,t,P,L,E,T) (1.6)

Determinarea parametrilor de raspuns necesita folosirea unui model matematic (analitic), care se formuleaza pe baza a trei tipuri de conditii pe care trebuie sa le îndeplineasca structura deformata sub actiuni:

conditii de echilibru (static sau dinamic);

conditii de compatibilitate geometrica;

conditii fizice (de comportare a materialelor constitutive).

Corespunzator acestor conditii se stabilesc trei tipuri de ecuatii (ecuatii de echilibru, ecuatii geometrice sau de deformatie si ecuatii fizice sau constitutive) care, împreuna cu conditiile la limita si cu cele de continuitate a deformatiilor, permit determinarea variabilelor alese ca necunoscute.

Trebuie precizat ca între diversele clase de parametri de raspuns exista relatii de legatura, încât pentru definirea completa a starii deformate a structurii este suficient sa se determine numai parametrii dintr-o anumita clasa (de exemplu, a deplasarilor prin metoda matricei de rigiditate sau metoda deplasarilor, respectiv a eforturilor sau tensiunilor prin metoda fortelor sau a matricei de flexibilitate).

În esenta, formularea unui model matematic pentru orice sistem fizic rezida în a stabili o relatie matematica între parametrii u si q, prin aplicarea legilor fizice caracteristice sistemului. Aceasta relatie, numita si ecuatie operationala, este de natura unui sistem de ecuatii de definitie de forma:

L(q₁, q₂,....,q_m, u₁, u₂,....,u_n) = 0 (1.7)

sau, mai compact

L(u) + f_v = 0 (1.8)

pe domeniul de definitie V al variabilelor u si q, unde L este un operator liniar sau neliniar, de tip algebric (matricial), diferential, integral sau integro-diferential.

La ecuatia operationala se ataseaza un set de conditii la limita, precizat prin relatia generica

C(q₁, q₂,....,q_m, u₁, u₂,....,u_n) = 0 (1.9)

sau compact

C(u) = f_s (1.10)

pe frontiera S a domeniului V.

În probleme stationare conditiile la limita sunt conditii de rezemare (pe contur, pe frontiera), iar operatorul C se poate nota C_f, în probleme nestationare sunt necesare si conditii initiale C_i la timpul de origine t₀.

Ecuatiile de definitie (1.8) împreuna cu conditiile la limita (1.10) constituie ecuatiile de guvernare ale sistemului, care au solutii de forma

u = u(q₁, q₂,....,q_m) (1.11)

În ecuatiile de guvernare L si C sunt operatori liniari sau neliniari, q sunt parametrii proprii si de intrare ai sistemului, u sunt necunoscutele problemei, iar f_v si f_s sunt functii date pe V respectiv S.

Exemple de ecuatii de guvernare

a)      Calculul deplasarilor w la încovoierea barelor drepte (fig. 1.3. a)

Ecuatia operationala: 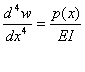( operatorul L=; p(x) - intensitatea încarcarii; EI - rigiditatea sectiunii la încovoiere);

Conditii la limita:

pentru x = 0 →w_A = w(0) = 0;

pentru x = l →w_B = w(l) = 0.

b)      Determinarea starii de tensiune la elemente structurale aflate în stare plana de tensiune (pereti structurali, plansee actionate în planul lor etc.) - fig. 1.3 b.

Ecuatia operationala:

Operatorul L=∆∆=∆²∆²= se aplica lui F(x,y) - functia de tensiuni sau functia lui Airy;

Conditii la limita (pe contur) - sub forma analogiei de cadru:

F_contur = M_cadru;

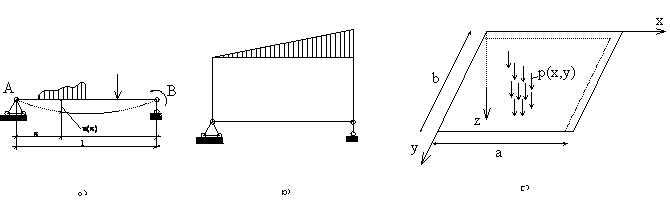Fig. 1.3

c)      Încovoierea placilor plane dreptunghiulare (fig. 1.3 c)

Ecuatia operationala:

Operatorul L=∆∆=∆²∆²= se aplica deplasarii normale w(x,y); D - rigiditatea placii la încovoiere.

Conditii pe contur:

x = 0 → w = 0;

x = a → w = 0; M_x = 0 →

y = 0 → w = 0; M_y = 0 →

y = b → w = 0;

Marimea unui parametru de raspuns (ca de exemplu deplasarea unui punct sau a unei sectiuni a structurii) poarta numele de grad de libertate (GDL). Întrucat acesti parametri de raspuns sunt functii continue de pozitia punctului sau sectiunii, rezulta ca structura are o infinitate de grade de libertate, care definesc starea deformata a acesteia. Din acest punct de vedere structurile reale ca si unele modele structurale de calcul pot fi considerate sisteme continue.

Adesea însa modelele structuralede calcul sunt prevazute cu un numar finit de grade de libertate (egal cu numarul n al parametrilor de raspuns necunoscuti u), caz în care structura este considerata un sistem fizic discret.

Problemele care apar la sistemele continue sau discrete se pot grupa în:

probleme stationare (de echilibreu si de valori proprii);

probleme nestationare (de propagare).

Componenta ecuatiilor de guvernare pentru fiecare tip de problema de mai sus este precizata în tabelul 1.1 (Pacoste).

Tabel 1.1

Exista mai multe posibilitati de analiza a comportarii unei structuri si de determinare a raspunsului acesteia.

Astfel, pentru proiectare este obligatorie efectuarea unei analize printr-un calcul de ordinul I liniar-elastic, care implica scrierea conditiei de echilibru static pe structura nedeformata (ipoteza micilor deplasari si a micilor deformatii), materialul având o comportare liniar-elastica.

La unele structuri ipoteza micilor deplasari nu mai este aplicabila,echilibrul trebuind sa fie scris pe structura deformata (neliniaritate geometrica), materialul având însa comportare liniar-elastica. Aceasta analiza printr-un calcul de ordinul al II-lea liniar-elastic, este necesara la structuri cu deplasari mari (structuri suspendate pe cabluri, structuri cu deschideri mari, structuri înalte si svelte -probleme de stabilitate).

La constructiile speciale, de importanta deosebita, la expertizari ale constructiilor existente, etc., pentru a stabili modul de cedare al structurii de rezistenta, se apeleaza la un calcul de ordin superior si la analize mai sofisticate, dintre care enumeram :

analiza elasto-plastica prin calcul biografic, când echilibrul se scrie pe structura nedeformata, iar materialul are comportare elasto-plastica;

analiza elasto-plastica bazata pe identificarea directa a mecanismului de cedare prin teoria plastica simpla;

analiza elasto-plastica bazata pe identificarea directa a mecanismului de cedare si luarea în considerare a efectului fortei axiale asupra formarii articulatiei plastice.

analiza neliniara cu luarea în considerare a ambelor tipuri de neliniaritate (geometrica si fizica);

Fazele principale ale modelarii precum si legaturile între parametrii implicati în procesul de proiectare sau expertizare a unei constructii se prezinta în fig. 1.4.

METODE DE CALCUL PENTRU DETERMINAREA RĂSPUNSULUI STRUCTURILOR

Determinarea parametrilor de raspuns, care sa satisfaca ecuatiile de guvernare ale unei structuri (ecuatia operationala si conditiile la limita aferente), se poate face prin doua tipuri de metode:

- metode analitice ("exacte"), care se bazeaza pe exprimarea variabilei de raspuns cautate prin functii analitice, valabil pentru orice punct al câmpului (domeniului) care se refera. Ca solutii analitice se pot folosi polinoamele algebrice, functiile transcendente elementare (trigonometrice, hiperbolice, etc.), seriile trigonometrice, seriile de puteri, functiile Bessel etc.

Gasirea unor solutii analitice însa, nu este posibila decât într-un numar redus de cazuri particulare de geometrie, rezemare si încarcare a structurii. Chiar si în acele cazuri, calificativul de solutie "exacta" nu îsi merita utilizarea pe deplin, deoarece modelul matematic pe care se opereaza are la baza un model fizic obtinut prin simplificari si idealizari ale structurii reale.

- metode numerice (aproximative) care constau în determinarea unor valori ale functiilor necunoscute (parametri de raspuns) dintr-un numar finit de puncte ale modelului structural (considerat sistem discret), sau a unor functii care sa aproximeze solutiile exacte, adica sa satisfaca, cu o eroare controlata si acceptabila, ecuatiile de guvernare. Daca functiile aproximante au ca domeniu de definitie întregul model structural, atunci aceasta are o infinitate de GDL (este un sistem continuu), iar daca definirea functiilor aproximante si determinarea lor se face numai pe subdomenii din modelul structural, atunci aceasta are un numar finit de GDL (este un sistem discret).

Întrucât volumul de calcule pe care îl implica metodele numerice este foarte mare, nu se poate vorbi de o folosire rationala a acestor procedee, decât în cazul cuplarii lor cu folosirea unor programe de calcul automat. Cu toate acestea, metodele numerice, de calcul au capatat o dezvoltare vertiginoasa o data cu dezvoltarea si cresterea performantelor calculatoarelor electronice.

Progresele în sectorul hardware antreneaza în paralel dezvoltarea si perfectionarea softului necesar (algoritmi, tehnici si metode numerice, programe de calcul, etc.).

Dintre metodele numerice (aproximative) se retin în continuare numai cele trei grupuri de metode, care pot fi formulate si pe cale matricilala []:

metodele matriciale directe, care au la baza teoremele lucrului mecanic virtual;

metodele variationale, care au la baza un criteriu de stationaritate impus energiei potentiale a structurii;

metodele reziduale, care se bazeaza pe conditia de stationaritate a functiei reziduale (functia reziduu exprima diferenta dintre solutia exacta si solutia aproximativa a problemei).

În cele ce urmeaza, se va aborda numai metoda elementelor finite (MEF), care actualmente este cea mai utilizata metoda numerica, întrucât ofera cele mai mari posibilitati, referitor atât la modelarea fizica a structurilor, cat si la procedurile numerice folosite. Formularea MEF se poate face utilizând oricare dintre criteriile considerate anterior în clasificarea metodelor numerice de calcul (fig. 1.5).

Fig.1.4

METODE DIRECTE Metoda fortelor Metoda deplasarilor METODA ELEMENTELOR FINITE (Metoda fasiilor finite) METODE VARIATIONALE Diferente finite Ritz Kantorovici Trefftz METODA ELEMENTELOR FINITE (Metoda fasiilor finite) Metoda elementelor de frontiera

METODE ENERGETICE

Fig. 1.5