|
Fig.2.2.1 |
Un tub de sticla vertical
de lungime L, īnchis la un capat contine aer, separat de
exterior cu ajutorul unei coloane de mercur de lungime h
= 20 mm. Cānd tubul este
asezat vertical, cu capatul
deschis īn jos , lungimea coloanei de aer este l1 = 0,39 m. Cānd tubul este vertical dar cu
capatul deschis īn sus ,
lungimea coloanei de aer este l2
= 0,37 m. Cunoscānd ![]() presiunea atmosferica
are valoarea :
presiunea atmosferica
are valoarea :
a. 1,01.105 N/m2; b. 0,94.105 N/m2; c. 1,2. 105 N/m2;
d. 0,8. 105 N/m2; e.1,3. 105 N/m2;
La mijlocul unui tub
asezat orizontal , īnchis la ambele
capete, de lungime L = 1 m se afla o coloana de mercur (![]() ) de lungime h = 0,2 m. Cānd tubul este adus īn
pozitia verticala, coloana de
mercur se deplaseaza cu l = 0,1 m. Sa se afle presiunea din tub
cānd se afla īn pozitia orizontala.
) de lungime h = 0,2 m. Cānd tubul este adus īn
pozitia verticala, coloana de
mercur se deplaseaza cu l = 0,1 m. Sa se afle presiunea din tub
cānd se afla īn pozitia orizontala.
a. 5.104 N/m2; b. 2. 104 N/m2; c. 2,5. 104 N/m2; d. 3. 104 N/m2; e. 104 N/m2.
Īntr-o camera de automobil cu volumul V = 1,2. 10-3 m3 presiunea aerului este pi = 0,5. 105 N/m2; Cāte apasari de piston trebuie sa se exercite asupra unei pompe de māna pentru a creste presiunea aerului la pf = 1,5. 105 N/m2, daca volumul pompei este v = 3.10-4 m3 iar presiunea aerului atmosferic po = 105 N/m2.
a. 5; b. 10; c. 15; d. 30; e. 40.
Un vas de volum V contine ![]() moli de gaz ideal
diatomic la temperatura to[C].
O fractiune f din molecule se
disociaza īn atomi. Presiunea finala a amestecului de gaze este :
moli de gaz ideal
diatomic la temperatura to[C].
O fractiune f din molecule se
disociaza īn atomi. Presiunea finala a amestecului de gaze este :
a. ![]() ; b.
; b. ![]() ; c.
; c. 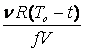 ;
;
d. 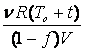 ; e.
; e.![]() .
.
Un cilindru orizontal īnchis la capete de lungime L = 1 m si sectiune S = 2.10-3 m2, este īmpartit īn doua parti egale printr-un piston mobil. Īn cele doua compartimente se afla aer la presiunea po = 105 N/m2. Se deplaseaza pistonul pe distanta h=0,4 m. Forta ce actioneaza asupra pistonului pentru deplasare are valoarea:
a. 444 N; b. 222 N; c. 111 N; d. 888 N; e. 1222 N.
|
Fig.2.2.6 |
Indicatiile unui barometru
cu mercur sunt eronate din cauza ca
īn tub a intrat o bula de aer. Cānd presiunea atmosferica este po = 1,013.105 N/m2,
barometrul indica ![]() , iar cānd presiunea
atmosferica este p = 0,957.105 N/m2,
barometrul indica
, iar cānd presiunea
atmosferica este p = 0,957.105 N/m2,
barometrul indica ![]() . Sa se afle īnaltimea L a tubului barometric (g
=10 m/s2;
. Sa se afle īnaltimea L a tubului barometric (g
=10 m/s2; ![]() (fig.2.2.6)).
(fig.2.2.6)).
a. 780 mm; b. 790 mm; c. 774 mm; d. 750 mm; e. 730 mm.
|
Fig.2.2.7 |
Un gaz īnchis īntr-un cilindru cu piston mobil (fig.2.2.7) se afla la temperatura T1 = 300 K. Sa se afle cu cāte grade variaza temperatura, daca volumul creste cu 20% , p = ct.
a. 30 K; b. 60 K; c. 90 K;
d. 120 K; e. 150 K.
Un gaz este īncalzit la presiune constanta de la temperatura T1 = 300 K la temperatura T2 = 400 K . Cu cāt la suta se modifica volumul gazului?
a. 11%; b. 22%; c. 33%; d. 44%; e. 55%.
Temperatura unui gaz scade izocor de la valoarea T1 = 400 K la T2 = 200 K. Sa se afle cu cāt la suta scade presiunea gazului?
a. 10%; b. 20%; c. 30%; d. 40%; e. 50%.
Īn doua recipiente se afla aer la temperatura T1 = 300 K si respectiv T2 = 400 K. Raportul dintre presiunile celor doua gaze este (p1/p2) = 3. Sa se afle raportul dintre presiunile celor doua gaze dupa ce sunt aduse la aceeasi temperatura.
a. 2; b. 3; c. 4; d.5; e. 6.
Doua baloane identice contin aer. Temperatura si presiunea īn cele doua baloane sunt T1, p1 si respectiv T2, p2. Baloanele sunt puse īn legatura iar gazele se amesteca , ajungānd la aceeasi presiune si temperatura. Din aceasta stare gazul este īncalzit la temperatura T. Sa se afle presiunea gazului p din sistem dupa īncalzire.
a.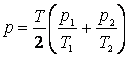 ; b.
; b.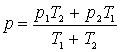 ; c.
; c. 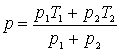 ;
;
d. 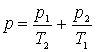 ; e.
; e. 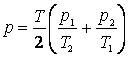 .
.
|
Fig.2.2.12 |
Un cilindru este īnchis la
ambele capete si contine un gaz oarecare, fiind īmpartit īn
doua parti de un piston mobil (fig.2.12). Īn cele doua
comportamente se afla aceeasi cantitate de gaz. stiind ca
la temperatura T raportul
volumelor este (V1/V2)
= n, sa se calculeze valoarea
raportului ![]() la temperatura
la temperatura ![]() . Se dau T1
= 300 K, n
= 5 si
. Se dau T1
= 300 K, n
= 5 si ![]() .
.
a. 3; b. 4; c. 5; d. 6; e. 7.
Īntr-un recipient īnchis, de volum V = 2 m3, se afla un amestec de azot biatomic (N) si oxid de azot (NO). Sa se afle masa m1 a oxidului de azot cunoscānd masa amestecului gazos, m = 14 kg, temperatura T = 300 K, iar presiunea p = 6.105 N/m2 (R = 8,31.103 J/kmol .K).
a. 5,4 kg; b. 4,3 kg; c. 3,2 kg; d. 2,1 kg; e. 7,6 kg.
Sa se afle presiunea unui gaz daca volumul V = 1 m3 contine un numar de N = 2,5.1028 molecule la temperatura de T = 300 K (k = 1,38.10-23 J/kg).
a. 1,03.105 N/m2; b. 2,09. 105 N/m2; c. 5,4. 106 N/m2; d. 8,4. 107 N/m2; e. 10,35. 107 N/m2.
Un balon de volum V = 2.10-3 m3 contine azot la temperatura T = 300 K si p = 1,38.10-4 N/m2. Sa se afle energia miscarii de translatie a tuturor moleculelor din vas (k = 1,38.10-23 J/K; NA =6,023.1026 molecule / Kmol).
a. 1,07.10-5 J; b. 2,3. 10-7 J; c. 4,14. 10-7 J; d. 6,2. 10-8 J; e. 7,3. 10-9 J.
Sa se afle presiunea la
care se afla un gaz , cunoscānd ca densitatea sa este ![]() iar viteza
termica a moleculelor
iar viteza
termica a moleculelor ![]() (HA = 6,023.1026mol/kmol).
(HA = 6,023.1026mol/kmol).
a. 0,25.105 N/m2; b. 0,50. 105 N/m2; c. 4,14. 105 N/m2;
d. 1,20. 105 N/m2; e. 105 N/m2;
Sa se afle exponentul
adiabatic ![]() pentru un amestec
gazos format din
pentru un amestec
gazos format din ![]() (He) si din
(He) si din ![]() (O2). Se
dau : CVHe =3R/2; CVO2
= 5R/2.
(O2). Se
dau : CVHe =3R/2; CVO2
= 5R/2.
a. 1,6; b. 3,2; c. 1,4; d. 1,2; e. 0,8.
Sa se calculeze caldura specifica a alamei, aliaj avānd compozitia procentuala: Cu 60% si Zn 40%. Se dau: cCu = 380 J/kg.K si cZn = 400 J/kg.K.
a. 388 J/kg.K; b. 270 J/kg.K; c. 340 J/kg.K; d. 420 J/kg.K; e. 350 J/kg.K;
Presiunea unui gaz ce ocupa volumul V1 = 2 m3, scade izoterm de la valoarea p1 = 8.105 N/m2 la valoarea p2 = 2.105 N/m2. Lucrul mecanic efectuat de gaz are valoarea (ln2 = 0,693):
a. 11.105 J; b. 22,2.105J; c. 32,3.103 J; d. 42,4.103 J; e. 52,3.105 J.
Un gaz ideal diatomic se destinde dupa legea p = aV, unde a este o constanta avānd valoarea a = 106 N/m5. Volumul final la care se ajunge este V2 = 20 l. Sa se calculeze lucrul mecanic efectuat de gaz.
a. 100 J; b. 200 J; c. 300 J; d. 400 J; e. 500 J.
|
Fig.2.2.21 |
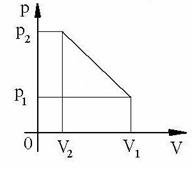
Īntr-un cilindru cu piston se afla m = 20 g He. Gazul sufera o transformare lenta (fig.2.2.21) din starea 1 īn care p1 = 0,41.106 N/m2, V1 = 32.10-3 m3 īn starea a doua īn care p2 = 1,6.106 N/m2 si V2 = 9 dm3. Sa se determine lucru mecanic efectuat.
a. 23,1.103 J; b. 20.102 J; c. 26.103 J;
d.25.103 J; e. 48,3.102 J.
Utilizānd datele din enuntul problemei 2.2.21, determinati temperatura maxima atinsa de gaz.
a. 496 K; b. 400 K; c. 396 K; d. 540 K; e. 480 K.
Sa se calculeze raportul dintre lucru mecanic efectuat īntr-o transformare adiabatica si una izoterma, la comprimarea unui volum de gaz de la V1 = 5 l la V2 = 1 l. (CV = 5R/2)
a. 1,2; b. 1,4; c. 1,6; d. 1,8; e. 2.
O cantitate de oxigen ocupa volumul V1 = 1 m3 si se afla la presiunea p1 = 2.105 N/m2. Gazul a fost īncalzit la p = ct. pāna la volumul V2 = 3 m3 si apoi la V = ct. pāna la presiunea p2 = 5.105 N/m2 (CV = 5R/2). Variatia energiei interne a gazului are valoarea:
a. 16,2.106 J; b. 32,5.105 J; c. 8.105J; d. 24,3.105 J; e. 30.106 J.
Utilizānd datele din problema 2.2.24, determinati lucru mecanic efectuat la trecerea din starea 1 īn starea 2.
a. 105 J; b. 2.105 J; c. 3.105 J; d. 4.105 J; e. 5.105 J.
O masa de azot m = 28.10-3 kg se afla īntr-un cilindru cu piston. Masa pistonului este m1 = 1 kg iar
sectiunea S = 10-3 m2. Gazul este īncalzit
izobar pāna la temperatura T2
= 400 K. Īn urma deplasarii
pistonului , energia potentiala a sa a crescut cu 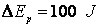 . Cunoscānd presiunea
atmosferica po = 105 N/m2 si Cp
= 7R/2, sa se afle volumul
initial ocupat de gaz.
. Cunoscānd presiunea
atmosferica po = 105 N/m2 si Cp
= 7R/2, sa se afle volumul
initial ocupat de gaz.
a. 10-2 m3; b 2. 10-2 m3; c. 3. 10-2 m3; d. 4 m3; e. 2 m3.
Utilizānd datele din enuntul problemei 2.2.26 determinati lucru mecanic efectuat.
a. 103 J; b. 1121 J; c. 1200 J; d. 1300 J; e. 1350 J.
|
Fig.2.2.28 |
Un tub cilindric vertical de
sectiuni diferite este īnchis la ambele capete prin doua pistoane de
sectiuni diferite (fig.2.2.28). Fiecare piston aluneca īn
portiunea de tub corespunzatoare. Īntre cele doua pistoane
legate printr-un fir inextensibil se gaseste un mol de gaz ideal.
Diferenta īntre sectiunile celor doua pistoane este ![]() , masa fiecarui piston este m iar presiunea
atmosferica este po.
Deplasarea l a pistonului se
obtine atunci cānd sistemul este īncalzit cu
, masa fiecarui piston este m iar presiunea
atmosferica este po.
Deplasarea l a pistonului se
obtine atunci cānd sistemul este īncalzit cu ![]() ,dat de relatia:
,dat de relatia:
a. ![]() ; b.
; b. ![]() ;
;
c.![]() ; d.
; d. 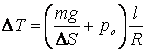 ; e.
; e. ![]() .
.
Utilizānd enuntul problemei 2.2.28, lucru mecanic efectuat de gaz are valoare:
a. ![]() ; b. pol; c.
; b. pol; c. ![]() ; d.
; d. ![]() ; e.
; e. ![]() .
.
Īn doua baloane izolate adiabatic fata de exterior se afla acelasi gaz. Parametrii de stare ai gazului din al doilea balon au valori de doua ori mai mari decāt parametrii de stare din primul balon. Cele doua baloane sunt puse īn legatura printr-un tub de volum neglijabil. Raportul dintre presiunea finala si presiunea initiala a gazului din primul balon este:
a. 5/3; b. 1; c) 2; d. 3; e. 3/5.
O masina termica ideala ce functioneaza dupa ciclul Carnot īntre temperaturile T1 = 400 K si T2 = 300 K produce īntr-un ciclu un lucru mecanic L = 80 kJ. Caldura cedata sursei reci are valoarea:
a. 80 kJ; b. 160 kJ; c. 240 kJ; d. 320 kJ; e. 40 kJ.
O masina termica ideala functioneaza dupa un ciclu Carnot reversibil īntre
temperaturile T1 = 1172 K si T2 = 293 K
avānd substanta de lucru o masa m
= 2 kg aer. Presiunea aerului la
sfārsitul destinderii izoterme este egala cu presiunea aerului la
īnceputul comprimarii adiabatice. stiind ca un ciclu se
efectueaza īn timp de 1 s (t = 1 s), sa se afle puterea consumata de masina (![]() ;
; ![]() ; ln2 = 0,693)
; ln2 = 0,693)
a. 1629 kW; b. 3254 kW; c. 2567 kW; d. 2900 kW; e. 1400 kW.
Utilizānd enuntul problemei 2.2.32, determinati puterea utila.
a. 2441 kW; b. 1220 kW; c. 610 kW; d. 3400 kW; e. 4400 kW.
Sa se calculeze randamentul unui ciclu Carnot efectuat de un gaz diatomic daca īn dilatarea adiabatica volumul gazului creste de la 6 m3 la 12 m3 (20,4 = 1,31).
a. 0,23; b. 0,46; c. 0,67; d. 0,34; e. 0,51.
O masina termica ce functioneaza cu carbune are un randament egal cu 80% din randamentul unei masini ideale ce ar lucra īntre aceleasi temperaturi extreme. Masina consuma timp de 1 h (t = 1 h) o cantitate de carbune mc = 23,8 kg cu puterea calorica q = 3,14.107 J/kg. Puterea utila a masinii are valoarea (T1 = 500K; T2 = 300 K) :
a. 1,1.105 W; b. 5.104 W; c. 4,8.104 W; d. 3,2.105 W; e. 5.105 W.
Doua corpuri cu masele, caldurile specifice si temperaturile initiale date: corpul 1, m1; c1, t1; corpul 2 m2 = m1/2 , c2 = 8 c1, t2 = 3t1/2 sunt introduse īntr-un calorimetru de capacitate calorica neglijabila. Pāna la atingerea echilibrului termic calorimetrul cedeaza īn exterior caldura q = 2 m1c1t1. Temperatura atinsa de corpuri la echilibru are valoarea:
a. t1/2; b. t1; c. 5t1/6; d. 10t1/11; e. 7t1/6.
Trei corpuri cu masele, caldurile specifice si temperaturile date: corpul 1 m1, c1, t1; corpul 2 m2, c2, t2; corpul 3 m3, c3, t3 īn care : m2 = 2m1, c1 = c2/2; t2 = 2t1; m3 = 3m1; c3 = c1, t3 = 4t1. Cele trei corpuri se introduc īn calorimetru cu capacitatea neglijabila. Temperatura de echilibru este:
a. 3t1; b. t1; c.t1/2; d. 3t1/2; e. 4t1/3.
Pe un cadru metalic cu aria S = 40 cm2 este formata o pelicula de apa cu
sapun. Sa se afle cu cāt se modifica energia peliculei daca
aria cadrului se micsoreaza la jumatate (T = ct. ![]() ).
).
a. -9,6.10-5 J; b. 4,6.10-5 J; c.9,6.10-5 J; d. 6.10-5 J; e. - 4.10-5 J.
Sa se calculeze coeficientul de tensiune superficiala a unui lichid daca se stie ca pentru desprinderea de la suprafata acestui lichid o rama metalica de forma unui patrat cu latura de 8,7 cm si masa m = 2 g este necesara o forta F = 0,035 N.
a. 7.10-3 N/m; b. 14.10-3 N/m; c. 21.10-3 N/m;
d. 28.10-3 N/m; e. 17.10-3 N/m;
Sa se calculeze energia eliberata prin
contopirea mai multor picaturi de glicerina de raza r = 5.10-4 mm īntr-o picatura mare de
raza R = 5 mm. (![]() )
)
a. 204.10-3 J; b. - 204.10-3 J; c. 102.10-2 J;
d. 402.10-3 J; e. - 402.10-3 J;
Un tub capilar asezat īn
pozitie orizontala contine ![]() coloana de
apa de cinci ori mai mare decāt īnaltimea ascensionala (l = 5 hmax). Adus īn pozitie verticala numarul
de picaturi ce curg din capilar este:
coloana de
apa de cinci ori mai mare decāt īnaltimea ascensionala (l = 5 hmax). Adus īn pozitie verticala numarul
de picaturi ce curg din capilar este:
a. 1; b. 2; c. 3; d. 4; e. 5.
Un vas comunicant avānd forma
literei U are ramurile formate din doua tuburi capilare. Cel din stānga
are diametrul d1 = 1 mm iar cel din dreapta d2
= 0,2 mm. Sa se afle
diferenta īntre nivelul lichidului īn cele doua ramuri cānd īn vas se
afla benzina (![]() ;
; ![]() ).
).
a. 1,6 cm; b. 5,6 cm; c. 4,9 cm; d. 8,9 cm; e. 12,3 cm.
O masa de 100 g apa
īncalzita de la t1
= 10oC absoarbe la
presiunea po = 105 N/m2 o cantitate de
caldura de 200 kJ. Volumul
ocupat de vaporii de apa are valoarea: (se cunosc: ![]() ;
; ![]() ;
; 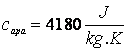 ;
; 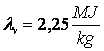 ).
).
a. 0,124 m3; b. 0,062 m3; c. 0,248 m3; d. 0,30 m3; e. 0,32 m3.
Īntr-un vas se afla īn
echilibru termic 150 g apa
si 50 g gheata.
stiind caldurile specifice 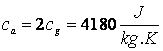 si caldura
latenta de topire a ghetii
si caldura
latenta de topire a ghetii 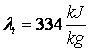 sa se determine
cāta caldura poate accepta sistemul fara a-si
modifica starea de echilibru termic.
sa se determine
cāta caldura poate accepta sistemul fara a-si
modifica starea de echilibru termic.
a. 22970 J; b. 16700 J; c. 6270 J; d. 1045 J; e. 24015 J.
Sa se afle caldura necesara
pentru a transforma īn vapori o bucata de gheata de masa m = 125 g, aflata la temperatura de 268 K (cg = 2090 ![]() ;
; 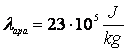 ;
; 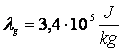 ;
; 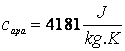 ).
).
a. 7,6.105 J; b. 2.105 J; c. 105 J; d. 8.105 J; e. 5.105 J;
Īntr-un calorimetru cu
capacitatea calorica neglijabila se introduce apa si
gheata. Se cunosc masele, temperaturile initiale si
constantele necesare; m1, c1, t1 pentru gheata; m2 = 2m1,
c2 = c1/2, t2
= -3t1. Caldura
latenta specifica a ghetii este ![]() . Īn acest caz la echilibru termic se obtine:
. Īn acest caz la echilibru termic se obtine:
a. t = - t1; b. t = t1/2; c. t = 0oC, masa de apa īn calorimetru 6m1/7;
d. t = 0oC, masa de apa īn calorimetru este 16m1/15;
e. t = 0oC, masa de apa īn calorimetru este 7m1/8.
|
Fig.2.2.47 |
Īntr-o galeata cu
capacitatea calorica neglijabila se afla 10 kg de amestec apa si gheata. Caldura
specifica a apei este 4200 J/(kg.K),
caldura latenta specifica de topire ![]() . Galeata a fost adusa īn camera iar
variatia de temperatura a sistemului īn functie de timp este
aratata īn figura 2.2.47 Īn timpul experimentului caldura
absorbita de sistem īn unitatea de timp este constanta. Īn momentul introducerii
īn camera masa ghetii a fost:
. Galeata a fost adusa īn camera iar
variatia de temperatura a sistemului īn functie de timp este
aratata īn figura 2.2.47 Īn timpul experimentului caldura
absorbita de sistem īn unitatea de timp este constanta. Īn momentul introducerii
īn camera masa ghetii a fost:
a. 1,23 kg; b. 0,72 kg; c. 1,46 kg; d. 1,8 kg; e. 0,5 kg.
Dintr-un vas īn care se
afla la temperatura t = 0o
C, se scoate rapid aerul. Ca urmare a
evaporarii rapide o parte din apa īngheata. Care este masa
de gheata ce se poate obtine īn felul acesta? (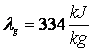 ;
; 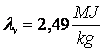 )
)
a. 88,17 g; b. 74 g; c. 16 g; d. 44,08 kg, e. 36 g.
Īntr-un vas cu V1 = 20 l se gasesc vapori saturati la t = 100oC. Care este lucru mecanic care trebuie efectuat pentru ca printr-o comprimare izoterma sa micsoram volumul vaporilor la V2 = 10 l? (Se neglijeaza volumul apei obtinuta prin condensare iar po = 105 N/m2).
a. 1kJ; b. 2 kJ; c. 1,39 kJ; d. 5 kJ; e. 10 kJ.
Se amesteca m1 = 5 kg apa la t1
= 5oC cu m2 = 10 kg gheata la t2
= - 15oC. Care este starea
finala a amestecului? (Se dau ca
= 4180 J/(kg.K); cg = 2090 J/(kg.K);
![]() ).
).
a. 15 kg apa; b. 15 kg gheata; c. 12 kg gheata; 3 kg apa;
d. 11,28 kg gheata, 3,72 kg apa; e. 10,625 kg gheata; 4,375 kg apa.
|