Subiectul 1
Introducere in cinematica:miscare,reper,spatiu,timp
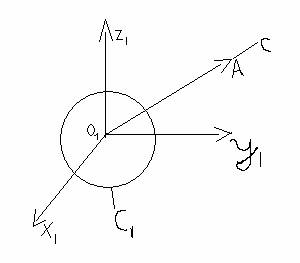 c-corp, c
c-corp, c![]() -corp
de referinta,O
-corp
de referinta,O![]() -observator
-observator
O![]() -zice
ca corpul c se afla in miscare da vee distantele pana la pc. lui c, variind in
timp.
-zice
ca corpul c se afla in miscare da vee distantele pana la pc. lui c, variind in
timp.
Miscarea-daca coordonatele pc. lor corpului C variaza in timp at. C se afla in miscare
(in rap cu
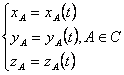
Spatiul-este absolute si metric
euclidian(dist![]() )
)
Timpul-este absolute(nu este influentat de material care umple spatial)
-este variabil independent
-se pune in corespondenta
-unitatea de timp secunda de tip atomic
Traiectoria-este locul geom..
al poz. successive ale pc. lui pt t>t![]() ,
e def.de ec. de miscare,parametrarea cu argum
,
e def.de ec. de miscare,parametrarea cu argum ![]()
Miscare poate fi def
prin: 1) TR: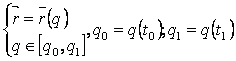
Viteza 2)legea de misc
pe TR: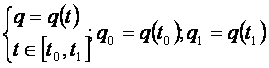
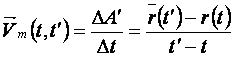
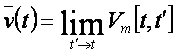
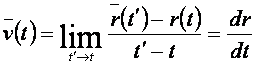
![]()
Acceleratia
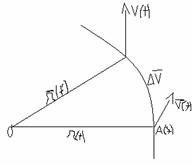
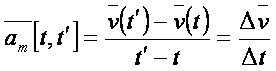
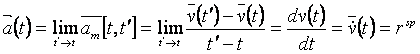
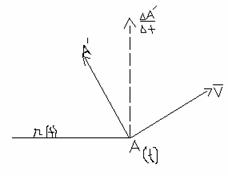
Deplasarea elemantara-este un
vectora coliniar si de acelasi sens cu viteza,dar de marime
infinitezecimala ->![]() -deplasarea elem la mom t pt cresterea dt a
timpului
-deplasarea elem la mom t pt cresterea dt a
timpului
Obs:deplasarea elem nu e
decat diferentiala ![]()
Subiectul 2 Coordonate carteziene.Miscarea rectilinie
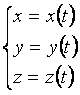
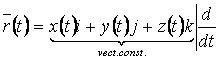
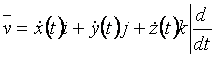 ;
; ![]()
 ;
; 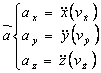
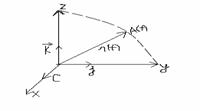
Coord polare
Reper polar-polul o;axa
polara ox;sens d.m aA![]()
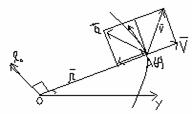 Baza atasata reperului polar-
Baza atasata reperului polar-![]() versorul
lui
versorul
lui ![]()
-![]() rotit
cu
rotit
cu ![]() ;-
;-![]() ; Coord polare-r = raza vect;
; Coord polare-r = raza vect;![]() =4
polar
=4
polar
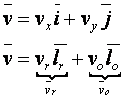
![]() viteza
radicala ;
viteza
radicala ; ![]() viteza
normala
viteza
normala
![]()
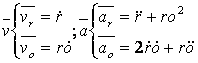
 ;
;![]()
![]() ;
; ![]() ;
; ![]() Reper cilindric(in sp)
Reper cilindric(in sp)
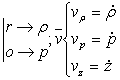 ;
; 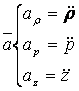
Sub 3- COORDONATE INTRINSECI
_ _ _
baza:βy,φ,ν-versori.
_
υ
![]()
 _ _ A1 -orig
axelor
_ _ A1 -orig
axelor
aυ φ φ - versorul tangentei dirijat in s.de m. a cerc
![]()
![]() a υ - versorul normalei
a υ - versorul normalei
![]()
![]() β β - versorul binormalei : β=φ^υ
β β - versorul binormalei : β=φ^υ
![]()
![]() _ A1
_ A1
aφ
Coordonate .
_ _
_ _ _
VA=(RӨ°)φ= (RӨ°) υ^β = R υ^ Ө°β = - Ө°β^ Ө°β = Ө°β^(-R υ)
R υ=AA'
w= Өk -viteza unghiulara a solidului
_ vA=w^AA' oricare ar fi A apartine S
A' proiectia lui A pe axa de rotatie
_ _
Mai general: vA=w^OA
_
VA →prOAvA=prOAv0
2.VITEZELE PUNCTELOR UNEI DREPTE DE DIRECTIE PARELELE SUNT EGALE
_ _ _ _
w||OA→vA=v0
3.PROPRIETATILE VITEZELOR PE w SUNT EGALE
_ _ _ _ _
vA*ww = v0* ww →prw*vA= prw*vB
4.C. in general nu exista in solid pct de viteza nul daca y0, v0=0 →y=0
z1
![]()
![]()
![]() z S
z S
![]()
 A_
A_
![]() _ _ rA y
_ _ rA y
![]()
![]() r1A r10 O
r1A r10 O
![]()
 O1
O1
y1 x
x1
SUB11 ANALOGIA STATICA
_ _ _ _
MA=M0+R^OA
_ _ _ _
vA=v0+w^OA
_ _ _ _
R →w M0→v0
-viteza variaza de la un pct la altul in solid dupa aceiasi formula dupa care variaza in statica mom resultant
_ _
ST: (R,M0) - tersor static
_ _
CINEM: (w, v0) - tersor cinematic(param cinematici)
AXA INSTANTANEE DE ROTATIE _ _
-exista puncte p in care viteza este coliniara cu w (vp||w). locul acestor pct este o
_
dreapta de directie w numita axa instantanee.
_ _ _ _
vA=v0+w^OA
_ _ _ _ _
vA=vp+w^pA→vp||w vp - componenta de translatie pA - comonenta de rotatie
ANALOGIE
{ y=0 din st (axa c) →axa instantanee de rotatie
REZ { R≠0
vp=0→vA=w^pA
_ _ _
ST: OP=R^M0 R2
_ _ _
CINEM: OP=w^v0 102 (w≠0)
SUB 12
![]() Miscarea generala a solidului
Miscarea generala a solidului
Formula acceleratiei. Campul de acc
![]() =
=![]() /
/![]()
![]() =
=![]()
![]() =
=![]()
![]()
![]()
![]()
![]()
![]() =
=![]() àformula acceleratiei
àformula acceleratiei
Campul de acceleratie
-Daca ![]() exista
j a.i. a=0 ; j=polul acc
exista
j a.i. a=0 ; j=polul acc
(coliniari)
-![]() dt
dt
a) ![]() invariant
invariant
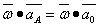
b) ![]() ànu exista pct de acc nula
ànu exista pct de acc nula
c) ![]() at
: exista pct de acc nula si locul lor este o dreapta de directia
at
: exista pct de acc nula si locul lor este o dreapta de directia ![]() ,
n. axa instantanee a acceleratiilor
,
n. axa instantanee a acceleratiilor
![]() SUB 13
SUB 13
Miscarea solidului in jurul unui punct fix:
Viteza si acceleratia. Deplasarea finite. Teorema lui Euler
-pct fix: este miscarea solidului in care un pct O al solidului este fix
Viteza: ![]()
![]()
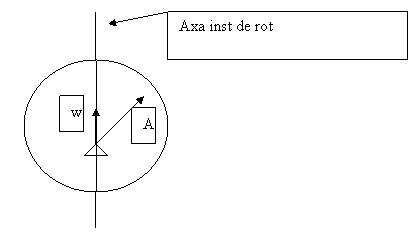

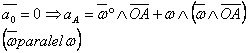
Deplasarea Finita
-deplasarea finite a solidului cu un pct fix se poate face prin rotatia in jurul unei axe plecand prin pct fix
Euler
-exista vectori ficsi la deplasarea solidului S dintro pozitie data intro alta pozitie
P=P' ; OP=OP'
DESEN EULER
(S.I.) 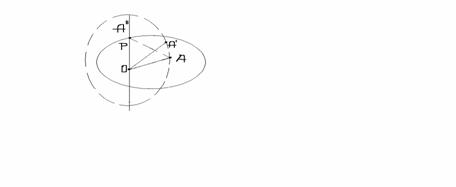
SUB 14
MISCAREA PLANA
Un solid
face miscare plana daca oriece pct al sau ramane la o distanta
AA'=ct
![]() fix
fix
S ![]() -sectiune(pl
mobil)
-sectiune(pl
mobil)
AB-directia
perpendiculara, ![]() -invariabil
-invariabil
-sens unic det
-modul constant àAB =const.
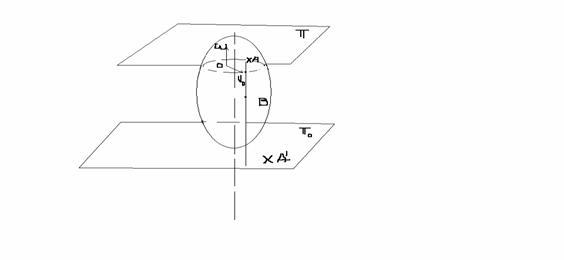
-orice sect plana a solidului cu un plan parallel cu planul director ramane intrun plan fix
Parametri cinematici

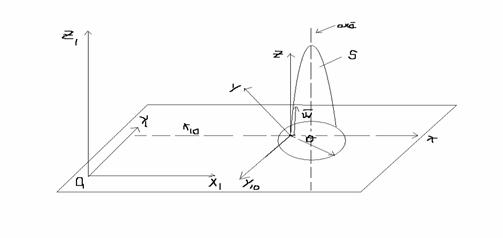
Ec de miscere (pt param cinematici)

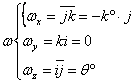 ;
; 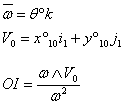
Centru instantaneu de rotatie
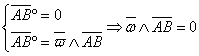 à
à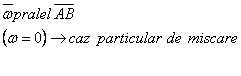
![]()
-Axa inst de rot=locul geom al punctelor de directie w
-I este
inst de rotatie al sectiunii S![]() ;
este seg pct care are v=0 la mom considerat
;
este seg pct care are v=0 la mom considerat
SUB 15
Distributie de viteze
In solid
AB
perpendicular pe S![]() ;
;
![]()
(AB paralel cu w)
a)Cu ![]()
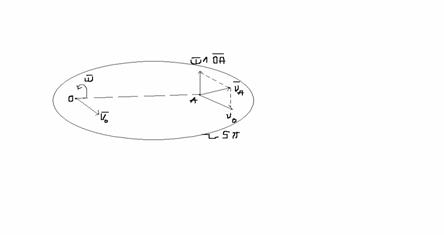
![]()
b)Cu I si w
![]()
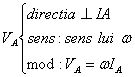
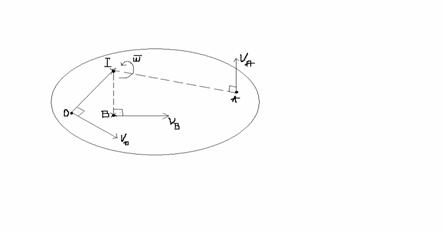
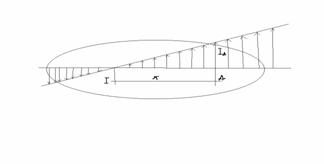
Distributia vitezei in lungul dr IA
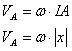
SUB 16
Miscarea plana
Distributia
si acceleratia S![]() Polul acceleratiilor distributia de acc in solid
Polul acceleratiilor distributia de acc in solid
Distributiade
acc in S![]()
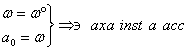
-intersectia
S![]() =j
=j
1)exista ![]()
2)![]()
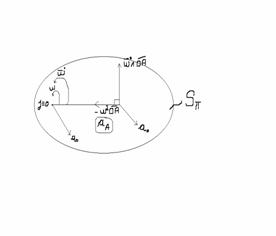
Distributia de acc in solid
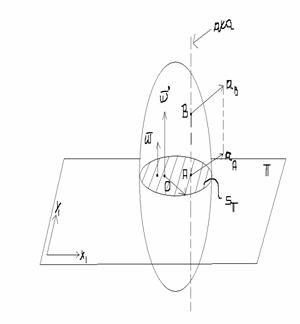

SUB 17
Miscarea plana
Det gometrica a centruluiinstantaneu de rotatie Exemple
![]()
1)disc care
se rostogoleste fara alunecare pe o curba fixa a pl ![]()

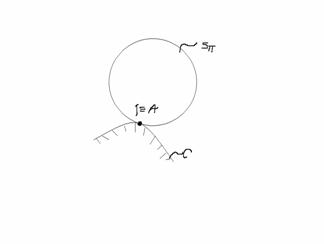

 2)
2)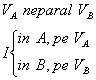
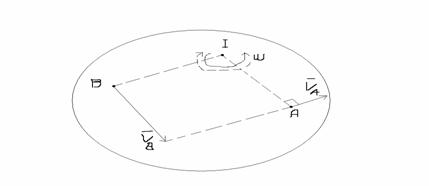
3)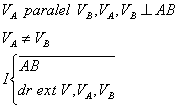
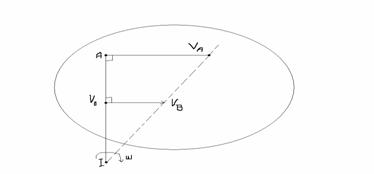
4)![]()
W=0àDistributia de viteze este ca intro translatie ànu exista I
![]() au acelesi sens a.i. este incal T
Proiectiilor
au acelesi sens a.i. este incal T
Proiectiilor
àaceleasi directii
àacelasi modul
SUB 18
Miscarea relative a pct
Repere si definitii
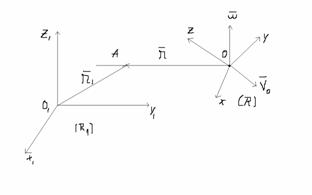
Se dau:
1)reperele R1,R
Se da miscarea R/R1
2)se da pct A in miscarea R si R1
1)Miscarea reperului Rfata de R1 se numeste miscare de transport
2)Misc lui A/R1 s. n. miscare absoluta
3)Misc lui A/R s. n. miscare relative
4) ![]() às. n. viteza relative
às. n. viteza relative
5) ![]() às. n. viteza absoluta
às. n. viteza absoluta
![]()
6) ![]() às. n. viteza de transport
às. n. viteza de transport
Se numeste miscare de transportare a pct A= miscarea pe care ar aveao pct A daca ar fi legat rigid de reperul R
SUB 19
Miscarea relative a punctului
Derivata absoluta si relative a unui vector
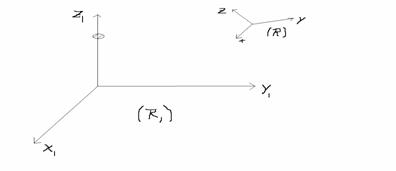
Obs 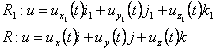
1) Derivata
lui u/R1 s. n. devivata absoluta, notatie ![]()
2) Derivata
lui u/R s. n. derivate absoluta, ![]()

SUB 20
Miscarea velativa a punctului
Formula vitezelor
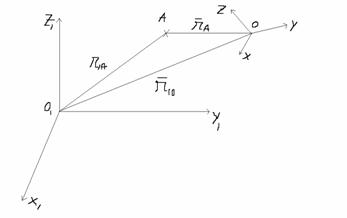

SUB 21
Miscarea relative a punctului
Formula acceleratiilor

SUB 22
Miscarea relative a solidului
Cente instantanee relative in miscarea plana: definitii; determinare geometrica; teoremele coliniaritatii
1)Def: Locul geometric al centrului instantaneu in planulfix ( sau urma lui I pe planul fix) este o curba numita BAZA.
2)Def:Locul geometric al centrului inst in plan mobil (urma luiIpe planul mobil) este o curba numita ROSTOGOLIRE.
Det geometrica
BAZA 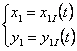 ROSTOGOLIRE
ROSTOGOLIRE 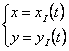

![]()
![]()
Rostogolire
Baza
![]()
![]()
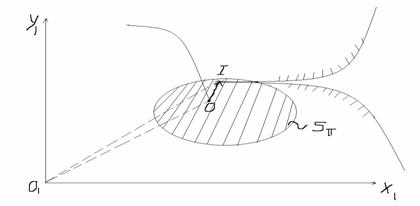
TEOREMELE COLINIARITATII
1) Cele 2 curbe sunt tangente in I (centrul inst de rotatie)
2) In
cursul miscarii placii S![]() rostogolirea se rostogoleste fara sa alunece peste baza.
rostogolirea se rostogoleste fara sa alunece peste baza.
T.C.-Determinam in prealabil cele 2 curbe si facand ca rostogolirea sa se rostogoleasca fara alunecare peste baza se reproduce miscarea din punct de vedere geometric.
SUBIECTUL 23
Principiile Mec. Clasice(Pr. Newtoniene)
Pr. Inertiei: un pct. Material nesupus la nici o actiune isi pastreaza la infinit starea de repaus sau de miscare rectilinie si uniforma
Pr. Act. Fortei: F=m*a
Pr. Independentei Actiunii Fortelor (paralelogram): daca forte aplicate unui punct mat. liber, au acelasi efect ca o sg. Forta aplicata pct. Reprezetata de diagonala paralelog. Cons. Pe cele 2 forte de laturi.
Pr. Reaactiunii: fortele cu care interactioneaza 2 pct. Materiale sunt direct opuse
![]()
![]()
![]()
![]()
![]() A1 A2
A1 A2
F12 F21
Pr. Conditiilor Initiale(Galilei): fortele de interact. Dintre 2 pct. Mat. sunt perfect determ. La orice mom. T daca se cunosc poz. Relative si vitezele relative ale celor 2 pct.
![]()
![]()
![]()
![]()
![]()
![]()
![]() A1 F12 F21 A2
A1 F12 F21 A2
![]() r12 V21=VA2/A1
r12 V21=VA2/A1
V21
F12=F21 (t, V12,V21) Forta-timp(t),-pozitie(r) F=F(t,r,v)-viteza(v)
6. Pr. De Relativitate: daca pp. dinamicii sunt vf. Intr-un reper Ratunci ele vor fi vf. In orice reper R' aflat in translatie rectilinie si uniforma R.
Problemele Mecanicii: 1. probl. Directa: se dau fortele care act. In system ul de corpuri . se cere misc. sist. 2. probl. Inversa: se dau misc. unui system de corpuri. Se cere sa se gaseasca forte care act. In systemul de corpuri
SUBIECTUL 24
![]()
 z A0(t)
z A0(t)
![]()
![]() Ec. Diferentiela Vectoriala: mr°°=F(t,r,v); A F1
Ec. Diferentiela Vectoriala: mr°°=F(t,r,v); A F1
r(t0)=r0, r°(t0)=v0![]()
![]() y
y
x
Ec. Carteziene consideratii analitice:
![]() mx°°=Fx(t,x,y,x°,y°,z°) x(t0)=x0,
y(t0)=y0, z(t0)=z0
mx°°=Fx(t,x,y,x°,y°,z°) x(t0)=x0,
y(t0)=y0, z(t0)=z0
my°°=Fy(t,x,y,x°,y°,z°) x°(t0)=x0,y° (t0)=x0,z°(t0)=z0
mz°°=Fz(t,x,y,x°,y°,z°) Nec. x(t),y(t),z(t)
![]() x=x(t) r0=x0*i+y0*j+z0*k
x=x(t) r0=x0*i+y0*j+z0*k
y=y(t) - sol ec. finale V0=Vox*i+Voy*j+Voz*k
z=z(t) r =x*i+y*j+z*k r° =x°*i+y°*j+z°*k
Probl.. unicitatii si existentei solutiei:
![]()
![]() z°=w, z°=1/m*Fz(t,x,y,z,u,v,w)
z°=w, z°=1/m*Fz(t,x,y,z,u,v,w)
y°=v , y°=1/m*Fy(t,x,y,z,u,v,w)
x°=u x°=1/m*Fx(t,x,y,z,u,v,w)
Consideratii analitice: Pp. ca s-a rezolvat sis. :
x=φ1(t) u= φ1(t)
y=φ2(t) v= φ2(t)
z=φ3(t) w= φ3(t)
Se numeste Integrala Prima a sist. Fctia F(t,x,y,z,u,v,w) cum propr. Ca
f(t,F1(t),.F6(t))= const.-integrala prima
SUBIECTUL 25
F A(t)
![]()
![]()
![]()
![]()
![]()
![]()
![]() lo
lo
![]()
![]() Ec. In
reper polar: ma=F(t,r,v)
Ec. In
reper polar: ma=F(t,r,v)
![]()
![]() mar
=Fr(t,r,v) lr O A0(t0)
mar
=Fr(t,r,v) lr O A0(t0)
![]() mao
=Fo(t,r,v) Oo
mao
=Fo(t,r,v) Oo
x
![]()
![]()
V Vr=r° a ar =r°°- ro
Vo=ro° ao =2r°o°- ro°°
![]()
![]()
![]() m(r°°-ro) =Fr (t,r,o,r°,o°) r(to)=ro
m(r°°-ro) =Fr (t,r,o,r°,o°) r(to)=ro
m(2ro°+ro°°) =Fo (t,r,o,r°,o°) o(to)=oo
----- ----- ----- conditii initiale
Ec. In reper cilindric: r→δ , o→φ
![]()
![]() m(δ°°- δ φ *φ)=Fδ(t,
δ,φ,z, δ°,φ°)
m(δ°°- δ φ *φ)=Fδ(t,
δ,φ,z, δ°,φ°)
m(2δ° φ° - δ φ°°)=Fφ (t, δ,φ,z, δ°,φ°) + z(t0)=zo
m z°° =Fz(t, δ,φ,z, δ°,φ°) z° (t0)=voz
SUBIECTUL 26
![]() Ec. In reper intrinsec: maζ= F(t,r,v) ms°°=Fζ(t,s,s°)
Ec. In reper intrinsec: maζ= F(t,r,v) ms°°=Fζ(t,s,s°)
maσ = Fσ (t,r,v) mi*i/ δ =Fσ (t,s,s°) + s(t0)=s0
maβ = Fβ (t,r,v) 0=Fβ(t,s,s°) j(t0)= Voζ
----cond initial
Pozitii de echilibru: poz. Ao se zice ,'poz de echilibru'' daca pct. Asezat in Ao, fara viteza, ramane indefinit la orice moment.
![]()
![]()
![]()

 σ ζ
σ ζ
F
 A(t)
A(t)
Mo![]()
![]()
![]() A0(t0) v0
A0(t0) v0
![]()
![]()
![]() A1
A1
S0
Pozitii de echilibru: poz. Ao se zice ,'poz. De echilibru''
Daca pct asezat in Ao fara viteza, ramane indefinit La orice moment
mr°°=F(t,r,v) existenta
r(to)=ro -------unicitatea
O1 O2 r°(to)=o(v=0) solutiei
F1 F2
![]()
A(m)
wg
Dem : to= poz. De echilibru == F'(t,ro,0)=0, orice t > 0 (rez se anuleaza in Ao)
Sub 27
![]() Teorema
Impulsului z A(t)
Teorema
Impulsului z A(t)
![]()
![]()

![]() v
v
Cantitatea H = m*vs*n*impuls
F mv
Sau cantitate de miscare
![]() H(t) = mv(t)àimpuls la moment y
H(t) = mv(t)àimpuls la moment y
H Hx = mvx = mx0
Hy = mvy = my0
Hz = mvz = mz0 X
![]() H=Hx*i+Hy*j+Hz*k // d/dt => H0=Hx0*i
+ Hy0*j + Hk0
H=Hx*i+Hy*j+Hz*k // d/dt => H0=Hx0*i
+ Hy0*j + Hk0
Hy0 = Fx La orice moment teorema derivata a impulsului
Hy0 = Fy => T. Impulsului = cu forta aplicata (rezultanta fortelor aplicate).
Hz0 = Fz
Cazuri de conservare
Fx = o => Hx=ct => mvx= ct. => Vx = ct. = Vox
![]() F = 0 conf.
Princ. Inertie v=ct = Vo
F = 0 conf.
Princ. Inertie v=ct = Vo
Aplicatii
F// axa => Tr. Plana si paralela cu axa
![]()
![]() z OZ//F
z OZ//F
![]() F
F
Fx = o => Vx = c1; Vx = dx/dt = c1=>
![]() Fy = o => Vy = c2 Vy = dy/dt = c2=>
Fy = o => Vy = c2 Vy = dy/dt = c2=>
o
j
x
=>dx/c1 = dy/c2=>c2dx - c1dy = o => d(c2x - c1y) = 0=> c2x-c1y = ct.
Sub 28)T. mom. cinetic: mom impulsului in rap cu un pct O sn mom kinetic in cu pct o.
Ko=r/mv -mom kinetic in rap cu o
Ko=KoxI+KoyJ+KozK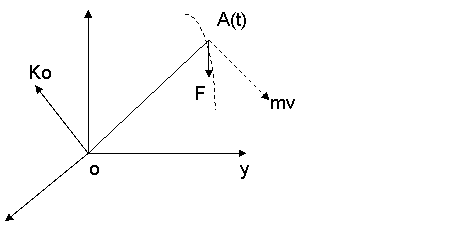

1)Reper cartezian Kox=m(z*y-y*z) Koz=m(xy*-yx*) !! *=o!! Koy=m(z*x-x*z)
I j k X y z X* y* z*
Ko=m
Er Eo k R 0 0 R* R*o 0
2)Coord polare Ko=m(r/v)=
T mom kinetic;la ori care ar fi mom t derivate mom kinetic in rap cu pct o =cu mom fortei aplicate in rap cu acelasi pct o. K*o=Mo(F)
DEM:Ko=m(r/v) Ko=r/mv; Ko*=r*/mv+r/m/v*=rma=r/F K*ox=Mox(F) K*oy=Moy(F) K*oz=Moz(F)-mom fortelor fata de
axele ox ox oz .
Sub 29)T.energiei cinetice ma=F mv*=F |vdt mvv*dt=Fvdt =>E=1/2mvv--.ener cinetica
d(mvv/2)=Fvdt Fvdt=Fdr=dδàlm elementar dEàdiferentiala Ec dδàlm
T1àdiferentiala Ec la mom t=lm al forteiin care actioneaza pct la mom t si pt dt. Eo= dδ/dt
T2àDerivata energiei=puterea la mom t
Forme ale teoremei Eº(t)tdt=dδ=Fvdt inmultim cu integrala de la t1 la t2
't1àt2Fvdt--.lm total in intervalul t1 t2 ; E1=E(t1); E2=E(t2); E2-E1=δ;
30)Calculul l.m total: δ12=integrala de la t1 la t2 di Fvdt
1)F=F(t,r,v); F depinde de toate variabilele conform teoremelor fundamentale ale mec. E necesar sa se cunoasca r =r(t) δ12=integr. De la t1 la t2 din F(t1,F(t),F*(t))ori(F(t,F(t),F*(t))dt=integrde la t1 lat2 oriФdt
F=F(r); Fàdepinde numai de pozitie
R=r(q)àec traiectoriei;q1:A1 q2 :A2;
Fie o lege arbitrara de miscare pe traiectorie q= q(t) unde q(t1)=q1 q(t2)=q2 ; δ12=integr.de le t1 la t2 din Fr(q(t))ori r'(q(t))q*(t)dt =integr.de le t1 la t2 din F(r(q)) r'(q)dq

3)Caz particular la 2):Exista U(r) a. i. F=grad U(r) ; U(r)=U(x,y,z,).
Exista U(xyz)a.i. F(x)=δU(xyz)/ δx; Fy=δU(xyz)/ δy; Fz=δU(xyz)/ δz
U se zice functie de forta iar relatia F=gradU se citeste 'F derivata dintro functie de forta. V(x,y,z.)= -U(x y z)àenergie potentiala.
δ12=integrala de la a1 la a2din(r(q))r'(q)dq=U(r2)-U(r1)=U(a2)-U(a1); E2-E1= δ12=U(a2)-U(a1); E2-U(a2)=E1-U(a1)àt. energiei
4)Exista U(xyz) ; dδ=dU(xyz); d(E-U(xyz))=0; E(t)-U(xyz)=ct. ; E-U=h=ct.=>integrala energiei.
31)Ecuatii.Forte de inertie.
R=oxyz; ma=F(t,r,v); R'=o'x'y'z'; aa=ar+at +acor
ar=a' ; m(a'+at+acor)=F(t,ro,r',v,vt); ma'=F-mat-macor
ma=fàforta de inertie
ma'=F+ft+fcor
-mat=ft ; -ma=fcor; ma'=F+ft+Fcor
Ec. de miscare: v'=D'r' a'=D'v'=D'D'r'
mx'=Fx'+(ft x' +(fcor x'
my'=....
mz'=....
Pozitii de echilibru relative:pct asezat fara viteza (relativa),intro pozitie raman la ori ce mom. In acea poz. F+ft=0 =>ec care dap oz. de echilibru.
32)Legaturi si forte de legatura.Metoda: principiul eliberarii de legaturi e valabil si in dinamica pc-lui dar reprez o met de lucru si nu o axioma.Princ elib. de legaturi: oricare system se poate considera ca liber suprimand legaturi si inlocuindu-le cu forte de legatura coresp. Pct liber: ma=F. pct legat ma diferit de F.=>rezultanta si acc. Nu au ac directie.
L=ma-F=> forta de legatura ;ma forta dinamica.Ec de misc: ma=F+L =>Princ.elib de legaturi care nu e o axioma ci o consecinta.Oricare ar fi probl. De pct. Legat se pot reduce la una de pct. Liber.

Sub. 33
Sistem Discret={Ai(ni); i=1,n}
 di= dist pct Ai la reperul
di= dist pct Ai la reperul
![]()
Mom de inertie fata de reperul R este suma maselor x patratul dist la reper.
Mom de inertie fata de un plan-plan ->planar
-axa ->axial
-pol ->polar
Continuum material
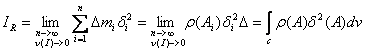
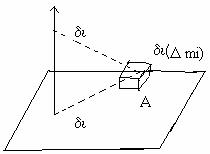 d(A)->continuum
bidimensional
d(A)->continuum
bidimensional
ds ->continuum unidimensional
Momente de inertie geometrice
I![]() ->mom de inertie geom.
->mom de inertie geom.
I![]() I
I![]()
![]()
![]()
![]()
![]()
Sub. 34
Deformarea in raport cu un reper Oxyz.
![]()
![]()
![]()
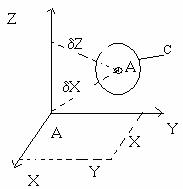
![]()
![]()
![]()
![]()
![]()
Matricea de inertie
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Sub 35
Deformarea cu reper O![]() .
Def unitara
.
Def unitara
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() |
|
![]() |
| ![]()
![]() |
|
![]() ; i=1,2,3
; i=1,2,3
![]() ; oricare i≠j ; I,j=1,2,3
; oricare i≠j ; I,j=1,2,3
![]()
![]() 0,
i≠j i,j=1,2,3
0,
i≠j i,j=1,2,3
1, i=j
Sub. 36
Variatia la translatia axelor
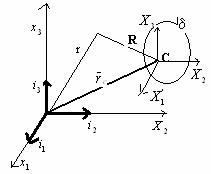
![]() - arbitrar
- arbitrar
![]()
![]() ;
;
c-centrul de masa al sistemului dat
![]()
I![]() =
[
=
[![]() ]
]
![]() -- T. lui
Steiner
-- T. lui
Steiner
![]()
![]()
![]() -
coordonatele sist dat
-
coordonatele sist dat
Particularizari pt mom centrifugale si axiale
![]()
![]()
![]() - mom centrifugale
- mom centrifugale
![]()
![]()
![]() +
+ ![]() - momentele axiale
- momentele axiale
![]()
![]()
![]()
Sub. 37
Variatia la rotatia axelor
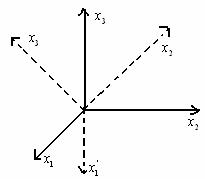
![]()
![]()
![]()
O marime def. de 9 coordonate ![]() ; I,j=1,2 si care la rotatia reperului se
modifica cu form
; I,j=1,2 si care la rotatia reperului se
modifica cu form ![]() s.n. Tensor de ordinal al-II-lea.
s.n. Tensor de ordinal al-II-lea.
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|
![]() => tensor simetric
=> tensor simetric
Tensorul de inertie
Mom de inertie def. de un tensor de ordin 2 simetric, s.n. tensor de inertie
Expresii matriciale ale legii de variatie
![]() à matricea tensorului in reperul
à matricea tensorului in reperul ![]()
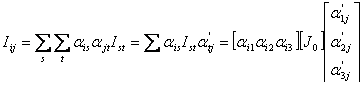
![]()
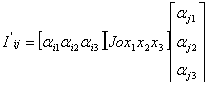
|