MARIMEA FIZICA SI MASURAREA

MĂrimeA fizicĂ si mĂsurarea

MĂrimea fizicĂ - definitii, clasificari

A. Se numeste marime (variable īn l.e, grandeur īn l.f.) o proprietate comuna pentru o clasa de obiecte, evenimente, stari, fenomene, procese, etc.

B. Marimea ce se poate evalua experimental, asa īncāt sa i se poata atasa o descriere simbolica (de tip numeric) se numeste marime fizica (sau marime masurabila); descrierea numerica atasata se numeste valoarea numerica a marimii fizice.

Dupa tipul simbolului matematic folosit pentru descrierea marimii fizice se identifica:

marimi fizice scalare, descrise doar prin intermediul unui numar real.

marimi fizice vectoriale, cu o descriere numerica n-dimensionala, componentele fiind de tip numar real;

marimi fizice tensoriale, descrise printr-o valoare numerica de tip matrice de numere reale, cu dimensiunile n, m; n este dimensiunea spat 838b11i iului īn care este descris tensorul iar m numarul de componente ce descriu o dimensiune a acestui spatiu.

C. Marimile fizice sunt notiuni abstracte si numai formele lor asociate unui obiect, eveniment, etc., pot fi descrise numeric prin masurare.

D. Dupa evolutia temporala a valorii numerice īntr-un interval de timp prestabilit, marimile fizice se grupeaza īn marimi de tip determinist si marimi de tip aleatoriu.

1D. Marimile de tip determinist (cu evolutie predictibila ) pot fi periodice sau neperiodice, dupa cum satisfac sau nu corelatia x(t)=x(t+kT), cu k numar īntreg iar T interval de timp de durata finita (numit perioada).

Marimile de tip periodic pot fi sinusoidale, compozite (combinatie lineara de marimi sinusoidale corelate -cu frecvente multipli īntregi ai unei valori numita frecventa fundamentala-) sau pseudoaleatoare (succesiune periodica a unui aceluiasi set de valori numerice ce sunt distribuite īntr-o perioada dupa o lege statistica prestabilita).

Marimile de tip neperiodic sunt: marimile cvasiperiodice (combinatie lineara de sinusoide necorelate), marimi de tip impuls (sau cu evolutie efemera), marimi de test (treapta, rampa, etc), s.a.

2D. Marimile de tip aleatoriu au o evolutie imprevizibila a valorii, putānd fi descrise doar pe baza unor observatii statistice.

MĂsurarea

1.2.1. Defini|ii

A. Masurarea unei marimi fizice atasate unui obiect sau eveniment real, reprezinta experimentul ce permite asocierea unei descrieri simbolice pentru marimea fizica respectiva. Experimentul poate presupune o singura operatie de evaluare a masurandului sau o succesiune de operatii (proces de masurare).

B. Marimea fizica ce face obiectul unei masurari se numeste masurand.

C. Formal masurarea reprezinta o operatie empirica si obiectiva de tip corespondenta univoca (homomorfism), M, avānd: ca multime de definitie, MPR -multimea manifestarilor individuale ale proprietatii ce defineste masurandul; ca multime a valorilor, MNU -submultime īn multimea numerelor reale, R; ca descriere a corespondentei, un set L de reguli empirice (de tip echivalenta, ordine, concatenare aditiva) ce, functie de specificul masurandului, poate fi definit pe MPR.

Ansamblul -ce sta la baza descrierii formale a masurarii- se numes-

te scara de masurare.

D. Procedura rationala de conducere a unei masurari se numeste metoda de masurare. Obiectele fizice specifice folosite īntr-o masurare se numesc mijloace de masura; ansamblul mijloacelor de masura implicate de o metoda de masura se numeste structura de masura.

E. Daca prin masurare se evalueaza nemijlocit masurandul, metoda de masurare si masurarea se numesc directe; daca pentru evaluarea masurandului se masoara direct alte marimi fizice, afate -fata de masurand- īntr-o corelatie cunoscuta apriori, metoda si masurarea se numesc indirecte.

F. Daca se realizeaza automat atāt masurarea cāt si memorarea valorii masurate se spune ca s-a realizat achizitia valorii masurate.

1.2.2. Tipuri de scĂri de mĂsurare

Diferentierea scarilor de masurare se face dupa structura corespondentei ce le defi-

neste (setul de reguli L). Exista patru tipuri de scari de masurare: nominala, ordinala, de raport, de interval.

A. Scara nominala, este definita numai pe baza unei relatii de echivalenta (egalitate a efectelor); valorile numerice obtinute au semnificatia unor "etichete numerice", singura prelucrare numerica fiind identificarea unei egalitati.

Exemplu: codului culorilor prin care se atribuie numere unor obiecte colorate diferit.

B. Scara de ordine, este definita prin relatii de ordine si de echivalenta; echivalenta -realizata prin masurare- cu un set de etaloane, stabileste numarul asociat masurandului (valoarea numerica a acestuia); relatia de ordine permite comparatia valorica īntre numerele obtinute prin masurare (de tip: mai mare, mai mic) dar nu si evaluarea un raport cantitativ (de tip: de atātea ori mai mare sau mai mic).

Exemple:scara Mohs pentru duritatea corpurilor, scarile Richter si Mercalli pentru intensitatea cutremurelor, scara Beaufort pentru taria vāntului.

C. Scari cantitative folosesc, īn plus fata de relatiile de echivalenta si de ordine, o relatie de concatenare (individuala sau de grup) prin care se permite definirea unui element etalon zis unitatea de masura a scarii; se poate astfel obtine descrierea numerica a masurandului prin valoarea raportului īntre el si unitatea de masura. Exista doua tipuri de scari cantitative: de raport si de interval.

1C. Scara de raport este definita pentru marimile fizice de tip extensiv (ce exprima proprietati aditive, precum lungimea, masa, intensitatea curentului electric, etc); unitatea de masura a unei asemenea scari se defineste explicit, printr-o marime fizica cu o valoare prestabilita.

2C. Scara de interval este definita pentru marimi de tip intensiv (ce exprima proprietati care nu sunt aditive, precum: temperatura, densitatea, permitivitatea electrica, s.a.); unitatea de masura a unei asemenea scari este descrisa implicit, printr-un interval (definit prin valorile sale extreme) care contine un numar prestabilit de unitati de masura.

Sistem de unitĂ|i de mĂsurĂ

1.2.3.1. Definitii, structura, conditionare

A. Se numeste sistem de unitati de masura, S_U, o reuniune de unitati de masura distincte ce permite masurarea tuturor marimilor fizice din unul sau mai multe domenii ale fizicii.

B. Un S_U contine trei categorii de unitati de masura: fundamentale, derivate si suplimentare.

Reprezinta unitati de masura fundamentale ale unui S_U, un ansamblu minim de unitati de masura independente care, prin relatii dimensionale simple, permit exprimarea unitatilor de masura derivate; unitatile de masura suplimentare sunt de tip fundamental dar cu arie restrānsa de utilizare.

C. Un sistem de unitati de masura trebuie sa īndeplineasca urmatoarele conditii: sa fie general, īn sensul de a permite masurarea a cāt mai multe marimi fizice; sa fie practic, adica potrivit masurarilor uzuale; sa fie coerent, ceea ce īnseamna ca relatiile prin care unitatile de masura fundamentale definesc unitatile de masura derivate nu contin coeficienti numerici; unitatile sale fundamentale sa fie usor de reprodus sub forma de etaloane.

1.2.3.2. Sistemul international de unitati de masura

#ncepānd din 1961 īn Romānia este acceptat oficial doar Sistemul international de unitati (SI).

SI are sapte unitati de masura fundamentale si doua suplimentare.

Unitatile de masura fundamentale din SI sunt: metrul (pentru lungime), kilogramul (pentru masa), secunda (pentru timp), kelvinul (pentru temperatura), amperul (pentru intensitatea curentului electric), molul (pentru cantitatea de substanta), candela (pentru intensitate luminoasa).

Unitatile de masura suplimentare din SI sunt: radianul si sterradianul (pentru unghiul plan respectiv pentru unghiul solid).

Valoarea numericĂ a mĂsurandului

1.3.1.Defini|ie

#n cazul general valoarea numerica a unui masurand reprezinta o descriere simbolica

(de tip numeric) rezultata experimental (prin utilizarea unei scari de masurare).

Deoarece pentru marimile electrice scarile de masurare sīnt numai de tip cantitativ valoarea numerica a unor asemenea marimi se mai poate defini ca fiind numarul real nenegativ care arata de cāte ori se cuprinde īn masurand unitatea de masura a sistemului de unitati de masura adoptat.

1.3.2. Exprimarea valorii numerice

1.3.2.1. Formatul de prezentare si conventia de reprezentare

Descrierea numerelor implicate īn indicarea valorii numerice a unui masurand (VANUM), presupune alegerea unui format de prezentare si a unei conventii de reprezentare.

Orice format de prezentare (FOP) este compus din cāmpuri de simboluri; atāt cāmpurile cāt si simbolurile au semnificatia fixata, fiecare cāmp avānd un numar finit de elemente. Principalele tipuri de FOP sunt: īntreg, real īn virgula fixa, real īn virgula mobila.

Conventia de reprezentare (COR) defineste simbolurile utilizate pentru descrierea cāmpurilor unui FOP, fiind īn esenta un cod numeric. Se folosesc:

Codul zecimal, daca VANUM este utilizata nemijlocit de experimentator;

Varietati de cod binar, atunci cānd un bloc numeric de calcul foloseste VANUM. Cele mai folosite coduri binare sunt: CBN -cod binar natural, ZCB -cod zecimal cu codificare binara, CCB -cod complement fata de doi, CBO - cod binar deplasat (offsetat).

1.3.2.2. Eroarea de cuantificare

Cum orice tip de FOP are un numar finit de componente ale cīmpurilor ce-l definesc, nu se pot descrie decāt un numar finit de valori distincte; deci descrierea unei VANUM implica, intrinsec, o aproximare.

Incertitudinea de exprimare a unei VANUM cu un FOP impus se numeste eroare de cuantificare si este egala cu cel mult jumatate din cea mai mica valoare ce poate fi exprimata folosind respectivul FOP.

Exemplu: daca pentru o tensiune se adopta exprimarea īn virgula fixa cu 4 cifre zecimale, de forma xx.xx V, eroare maxima de cuantificare este de 5mV.

1.3.2.3. Conditionarea exprimarii valorii numerice

FOP si COR sunt impuse de utilizator. Daca utilizatorul este uman, COR este numai de tip zecimal iar FOP este de tip īntreg sau real virgula fixa; daca utilizatorul este un echipament numeric, COR este numai de tip binar iar FOP poate fi de orice tip.

Pentru un COR dat, deschiderile cāmpurilor din FOP sunt alese functie de eroarea de cuantificare maxim admisa si de limitele intervalului de existenta a VANUM ce se reprezinta.

Exemplu: pentru exprimarea zecimala unor valori īn gama 0.1..1999 cu o eroare de cuantificare de cel mult 0.02 se va alege un FOP de forma XXXX.XX; daca eroarea maxima de cuantificare admisa este 0.05, FOP este de forma XXXX.X.

1.3.3. Suportul fizic al valorii numerice

1.3.3.1. Semnal, modulatie

Atunci cānd o valoare numerica masurata trebuie afisata, transmisa la distanta, memo-

rata, i se asociaza un suport informtional, numit semnal (sau marime suport sau marime modulata); pentru cazul masurarilor electrice, cel mai adesea semnalul este de tip curent sau tensiune.

#ncorporarea īntr-un semnal a informatiei se numeste modulatie; principalele tipuri de modulatie sunt: īn amplitudine, īn frecventa, īn faza, īn factor de umplere, īn cod.

1.3.3.2. Modulatia īn cod

#n masurari, modulatia īn cod tinde sa fie folosita preponderent datorita unor avantaje importante: obtinerea unei acurateti deosebite a transferului informational; stocarea si prelucrarea complexa a informatiei; reducerea complexitatii constructive si a pretului echipamentelor implicate (datorita gradului mare de integrare al circuitelor numerice).

Semnalul de iesire al unui modulator īn cod, este de obicei de tip tensiune sau curent si se numeste uzual marime numerica.

Marimea numerica descrie, prin reguli (conventii) -proprii COR folosita- exact valoarea numerica careia īi este asociata; fara exceptii COR sunt numai varietati de cod binar.

Una din cele mai folosite conventii pentru descrierea efectiva (fizica) a marimilor numerice este conventia TTL definita prin: marimea fizica utilizata - tensiune; nivelele ce descriu valorile logice binare (conventia pentru o iesire numerica) -unu logic ... 2.4V, zero logic ... 0.4V (valori adevarate pentru nivele impuse ale curentului de iesire maxim).

1.3.4. Descrieri matematice asociate marimilor fizice si masurarii

1.3.4.1.Pentru marimile de tip determinist

1.3.4.1.1. Cazul general

A. #n cazul marimilor fizice de tip determinist principalele descrieri matematice cu semnificatie pentru domeniul masurarii privesc evolutia temporala. Asemenea descrieri se pot face: explicit -printr-o functie de timp-; implicit -prin solutia unei ecuatii (algebrica sau diferentiala)-; sintetic -printr-un set de coeficienti si o "baza de functii prestabilite". Dintre aceste variante ultima este īntotdeauna posibila (cel putin ca o aproximare corectabila).

B. Descrierile de tip sintetic ale unei evolutii temporale x(t) privesc un interval de observare finit t₁,t₂ si folosesc o combinatie lineara de functii de timp cunoscute (reale sau complexe), ; evolutia x(t) este aproximata prin:

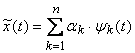(1.3.1)

setul de coeficienti numerici reprezentānd descrierea sintetica a lul x(t) fata de

setul de functii

Pentru ca descrierile sintetice sa fie cāt mai simple setul de functii Y sunt de tip ortogonal (ceea ce īnseamna ca produsul scalar pe intervalul t₁,t₂ este nul daca k l, daca k=l produsul scalar devine egal cu patratul normei, valoare notata l_k ) sau ortonormat (l_k=1); īntr-un asemenea caz:

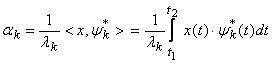(1.3.2)

Daca setul de functii ortogonale este complet (n ) atunci eroarea medie patratica de aproximare prin (1.1.1) a lui x(t) tinde spre zero.

C. Principalele ansambluri complete de functii ortogonale sunt: functiile Walsh (ansamblu de functii binare -ce au doar valorile 1 si -1, in intervalul deschis 0..T functia de ordin k schimbāndu-si de k ori semnul), poligoanele ortogonale (Jacobi, Legendre, Lageurre, Hermite si īn special Cebāsev) si functiile ortogonale exponentiale (cu W p/T, T fiind t₂-t₁) ce stau la baza seriilor Fourier. 

1.3.4.1.2. Pentru marimi periodice

Orice marime periodica de perioada T, x(t), se poate dezvolta īntr-o serie trigono-metrica:

(1.3.3)

īn care:

X₀ reprezinta componenta constanta, definita prin:

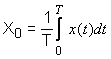(1.3.4)

x_k(t), k=1.. , marime sinusoidala, de perioada T_k=T/k , numita armonica de ordinul k a marimii periodice x(t). Armonica de ordinul īntāi, x₁(t), se numeste fundamentala, toate celelalte armonici reprezentānd reziduu deformant (deoarece ele determina abaterea marimii alternative de la o forma sinusoidala).

Descrierea analitica a armonicii de ordinul k este:

(1.3.5)

īn care:

w p/T -pulsatia marimii periodice x(t);

X_k -valoarea efectiva a armonicii x_k(t), legata de x(t) prin relatiile:

(1.3.5)

A_k, B_k, numite componente īn cuadratura, se determina cu:

(1.3.6)

j_k -faza armonicii x_k(t), determinata prin:

(1.3.7)

Multimea :

(1.3.8)

reprezinta structura spectrala a marimii periodice x(t); descrierea unei marimi periodice prin componente spectrale reprezinta cea mai completa descriere sintetica.

Daca pentru x(t) se foloseste o descriere trunchiata, īn relatia (1.3.3) suma limitāndu-se la k=N, se recomanda utilizarea aproximarii Lanczos -ce da bune rezultate īn special cānd evolutia x(t) contine puncte de discontinuitate-:

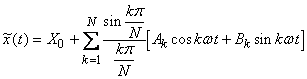(1.3.9)

X₀, A_k, B_k īsi pastreaza semnificatiile din (1.3.4), (1.3.6).

1.3.4.2. Pentru marimile de tip aleatoriu

A. In cazul general o marime aleatoare se caracterizeaza prin lipsa oricarei relatii ce sa-i permita predictia (atāt ca evolutie temporala cāt si ca evolutie repetabila).

B. Cea mai simpla marime aleatoare este o functie de doua variabile X (x,t), t fiind timpul, x luānd valori īn domeniul de valori al marimii X.

Descrierea lui X(x,t) se face numai statistic prin: functia de repartitie a probabilitatii, densitatea de probabilitate, media si dispersia statistica, media si dispersia temporala, functiile de autocorelatie si intercorelatie.

C. Valoarea medie statistica īntr-un moment de timp t₁ dat, se defineste ca media, la momentul t₁, a tuturor realizarilor posibile ale lui X(x,t):

(1.3.10)

M definind operatorul de mediere.

La momentul t₁,oarecare, dispersia statistica este:

(1.3.11)

s_x numindu-se eroare medie patratica.

Similar relatiilor (1.3.10), (1.3.11), se definesc media respectiv dispersia temporala, luīndu-se īn considerare o evolutie oarecare X(x,t).

Observatie: Daca m_x(t₁) si s_x(t₁) sunt constante īn timp atunci X(x,t) se numeste marime aleatoare stationara; daca pentru o asemenea marime media statistica este identica cu media temporala marimea aleatoare se numeste ergodica. Uzual marimile aleatoare se considera ergodice, deci proprietatile lor statistice pot rezulta din analiza unei singure evolutii temporale, oricare din cele posibile.

D. Descrierile matematice asociate marimilor de tip aleatoriu cu semnificatie pentru masurari privesc īn principal legile statistice ce definesc evolutia probabila; pe baza acestora se pot face evaluari privind corectitudinea masurarii (analiza erorilor de masurare).

1.3.5. Valori numerice specifice

1.3.5.1. Tipuri de valori numerice

Functie de obiectul sau fenomenul fizic caruia īi este atasat masurandul, descrierea simbolica rezultata prin masurare priveste fie valoarea momentana, fie o valoare sintetica (raportata la un ansamblu prestabilit de valori momentane) a marimii fizice respective.

Pentru fiecare dintre aceste valori, prin raportare la momentul "citirii" informatiei, descrierea poate fi: de tip indicator (sau punctuala) -prin prezentarea valorii temporale raportata la momentul prezent (al citirii); de tip īnregistrator -prin prezentarea desfasurata a evolutiei temporale dintr-un interval de timp anterior momentului prezent; de tip integrator - prin prezentarea cumulata a unor valori temporale anterioare timpului prezent.

1.3.5.2. Valori numerice sintetice

1.3.5.2.1.Justificare

Valorile numerice sintetice s-au definit pentru urmarirea eficienta a evolutiei marimilor fizice; ele descriu aspecte particulare ale marimii fizice, fiind relevante numai pentru o anumita analiza. Uzual se definesc valori sintetice numai pentru marimile periodice si pentru marimile aleatoare.

1.3.5.2.2.Valori sintetice definite pentru mĂrimi periodice

Pentru marimea periodica M_x - ce descrie procesul fizic P_x-, functie de aspectele specifice ale procesul fizic P_x care doresc sa fie evidentiate prin masurarea lui M_x, se utilizeaza una sau mai multe din urmatoarele valori sintetice: valoarea efectiva, valoarea de vārf, valoarea de c.c.,factorul de distorsiuni, factorul de forma, factorul de creasta.

Daca pentru un interval de timp (mult mai mare decāt o perioada) valorile sintetice ale marimii periodice sunt constante marimea se numeste stabilizata.

A.Valoarea efectiva, valoarea de vārf, valori medii

Definita pentru a descrie aspecte energetice, valoarea efectiva, X_ef, reprezinta cea mai utilizata valoare sintetica; se defineste prin relatia:

(1.3.12)

Utilizata pentru a descrie fenomene de saturatie, valoarea de vīrf se defineste ca fiind maximul, dintr-o perioada T, al valorii absolute ; uneori se definesc distinct maxi-

mul pozitiv si maximul negativ.

Numita si valoarea medie īntr-o perioada, valoarea de c.c., X_CC, se utilizeaza pentru a descrie fenomene constante sau cumulative si se defineste prin relatia (1.3.3)

Numai pentru o marime alternativa, care īndeplineste conditia x(t)=-x(t+T/2), se defineste valoare medie pe semiperioada X_med, prin:

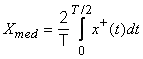(1.3.13)

descrie evolutia lui x(t) īn semialternanta pozitiva.

Deoarece exista relatia echivalenta:

(1.3.14)

X_med se mai numeste si valoare medie redresata (un redresor ideal avānd o caracteristica intrare-iesire de tip functie modul).

C. Factor de forma, factor de distorsiuni, factor de creasta

Factorul de forma, K_F, definit numai pentru marimi alternative, permite o descriere sintetica a abaterii de la forma sinusoidala; K_F se defineste prin:

(1.3.15)

X_ef si X_med fiind definite prin (1.3.12), respectiv (1.3.13). Pentru o marime sinusoidala factorul de forma este:

(1.3.16)

Definit numai pentru marimi alternative, factorul de distorsiuni, K_d, este o descriere derivata din descrierea spectrala, punānd īn evidenta influenta energetica a reziduului deformant fata de fundamentala; K_d se defineste prin:

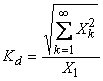(1.3.17)

īn care X_k, k=1.. , este valoarea efectiva a armonicii k (din dezvoltarea īn seie Fourier). Evident pentru marime sinusoidala K_d=0.

Factorul de creasta, K_c, se defineste prin relatia:

(1.3.18)

pentru marime sinusoidala , pentru marimi nesinusoidale fiind acceptate valori īn gama 2..10.

D. Observatie

Cerinta de masurare frecventa a unor valori sintetice -precum valoarea efectiva, factorul de forma, componentele spectrale- a impus constructia unor mijloace de masurat specializate.

1.3.5.2.3.Valori sintetice definite pentru mĂrimi aleatoare

Pentru marimi aleatoare, valorile sintetice utilizate curent sunt media si dispersia statistice.

Sunt foarte rare mijloace de masurat dedicate determinarii valorilor sintetice ale marimilor aleatoare, de obicei operatiile matematice presupuse prin relatiile de definitie (precum 1.3.10, 1.3.11) implementāndu-se, computerizat, folosind īnregistrarea numerica a respectivelor multimi de valori.

Bibliografie

1.1. Aurel Millea, Masurari electrice -principii si metode. ET, 1980.

1.2. Paul Manolescu, Carmen Golovanov, Masurari electrice si electronice,EDP 1980.

1.3. Emil Pop, s.a., Tehnici moderne de masurare. Ed. Facla, 1983.

1.4. Constantin Iliescu (coord.), Masurari electrice si electronice. EDP, 1983.

1.5. Gabriel Ionescu, Masurari si traductoare. EDP, 1985.

P. Paratte, Ph. Robert, Systemes de mesure, P. Polytech. Romandes, 1986.

1.7. F. de Coulon, Theorie et traitement des signaux, P. Polytech. Romandes, 1990.

1.8. A. Poularikas, S. Seely, Signal and Systems, PWS -KENT Publ. Comp., 1991