Polarizarea dielectricilor

Polarizarea dielectricilor

1.7.1. Starea de polarizație

Corpurile a căror densitate de sarcină electrică (adevărată) este în fiecare punct nulă, numite și corpuri neutre, se împart în două clase:

- corpuri neutre nepolarizate electric, care dacă sunt introduse în orice fel de câmpuri electrice (omogene sau neomogene) nu sunt supuse unor acțiuni ponderomotoare (forțe sau momente);

- corpuri neutre polarizate electric, care dacă sunt introduse în câmpuri uniforme cu orientări potrivite sunt supuse la cupluri, iar dacă sunt introduse în câmpuri neuniforme cu orientări potrivite sunt supuse și la forțe.

Corpurile polarizate electric pot fi încărcate în același timp și cu sarcină electrică (adevărată).

Starea corpurilor mici polarizate electric se caracterizează cu ajutorul unei mărimi de stare vectorială 24224c219y , numită moment electric. Starea locală a corpurilor masive polarizate se descrie cu ajutorul densității de volum , a momentelor electrice, numită polarizație electrică.

Polarizația electrică poate fi:

- permanentă, dacă nu depinde de intensitatea locală a câmpului electric;

- temporară, dacă depinde de intensitatea locală a câmpului electric în care este situat corpul.

Polarizația permanentă poate apare sub formă de:

polarizație piezoelectrică, prezentată de anumite cristale care se polarizează prin

deformare mecanică;

polarizație piroelectrică, prezentată de anumite cristale care se polarizează prin încălzire;

- polarizație permanentă a electreților (analogii magneților permanenți, în cazul stărilor electrice), prezentată de anumite materiale (rășini, plexiglas, ceruri) după ce au fost supuse unei încălziri prealabile, până la înmuiere, într-un câmp electric foarte intens și au fost lăsate să se răcească în acest câmp.

1.7.2. Momentul cinetic

Experiența arată că acțiunile ponderomotoare care se exercită asupra unui mic corp polarizat (permanent sau temporar) adus în vid, într-un câmp electric exterior de vector câmp , adică cuplul și forța exercitate în aceste condiții asupra micului corp, sunt date de relațiile:

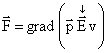
În a doua relație, săgeata indică mărimea care se derivează, astfel că proiecțiile forței pe axe sunt:

Această forță e nulă într-un câmp omogen .

Mărimea care apare în aceste relații este o mărime primitivă de stare a micului corp polarizat, depinzând de starea lui globală de polarizare, caracterizând complet această stare, și se numește moment electric al corpului.

Momentul electric total: , unde: este momentul electric permanent, iar reprezintă momentul electric temporar.

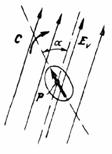
Fig. 1.13

Din figura 1.13 rezultă - în cazul particular al unui corp polarizat permanent, la care e constant și independent de - că acest corp are o direcție proprie de polarizație (direcția lui ), care tinde să se așeze paralel cu direcția câmpului electric (conform sensului de rotație definit de produsul vectorial ).

1.7.3. Polarizație electrică

Mărimea ce caracterizează starea locală de polarizație a unui corp masiv se numește polarizație electrică. Se numește polarizație electrică o mărime derivată definită de limita raportului dintre suma vectorială a momentelor electrice ale materialului dintr-un volum Dv și acest volum, când el tinde către zero:

. (1.37)

- polarizația electrică se mai numește și intensitate de polarizație. Ea poate fi scrisă și ca sumă dintre intensitatea de polarizație temporară și permanentă:

. (1.38)

Dacă se cunoaște se poate determina cu relația:

. (1.39)

1.7.4. Unități de măsură

Unitatea de moment electric în sistemul MKSA este metru - coulomb (Cm),

.

Unitatea de măsură pentru polarizație este coulombul pe metru pătrat (C/m²).

1.7.5. Sarcini de polarizație. Densitatea sarcinii de polarizație

Se consideră volumul unui corp polarizat împărțit în elemente de volum în lungul liniilor de polarizație, fiecare element de volum se poate înlocui cu un dipol (fig. 1.14). Excesul local de sarcini dipolare de un nume față de cele de nume contrar dă sarcina electrică de polarizație .

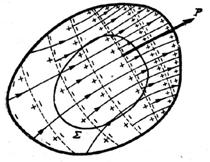
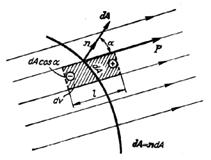
Fig. 1.14 Fig. 1.15

Considerând o suprafață închisă S, ea va avea exces de sarcini (negative în acest caz). Acest exces de sarcini este determinat numai de frontieră, care intersectează dipolii, deoarece sarcinile dipolilor din interior au suma nulă. Pentru un element de volum (fig. 1.15) cu baza dAcosa și lungimea l, în interiorul suprafeței S, sarcina este .

. (1.40)

Sarcina dipolară corespunzătoare rămasă în interior și care contribuie la sarcina de polarizație q_p din S, e de semn contrar:

(1.41)

iar sarcina totală de polarizație q_p din "interiorul" suprafeței S rezultă:

. (1.42)

Sarcina electrică de polarizație localizată în interiorul unei suprafețe închise este egală și de semn contrar cu fluxul polarizației electrice prin acea suprafață.

Dacă se introduce noțiunea de densitate superficială a sarcinii de polarizație, se obține:

. (1.43) Relația (1.43) arată că vectorul polarizație , este numeric egal cu densitatea superficială a sarcinii de polarizație r_sp

Prin urmare unitatea de măsură a polarizației este colombul pe metru pătrat (C/ m), iar a momentului dipolului este coulomb înmulțit cu metru (C. m.).

(1.44)

Relația (1.44) reprezintă forma integrală a expresiei sarcinii de polarizație. Prin urmare sarcina electrică de polarizație localizată în interiorul unei suprafețe închise , este egală și de semn contrar cu fluxul polarizației electrice prin acea suprafață. Notând cu q_VP, densitatea de volum a sarcinii de polarizație, se obține sarcina de polarizație din volumul

. (1.45) Aplicând formula lui Gauss - Ostrogradski relației (1.44) și egalând-o cu (1.45) rezultă:

(1.46)

care este forma locală a expresiei sarcinii de polarizație.

1.7.6. Rigiditatea dielectrică

Dacă se introduce un dielectric într-un câmp electric foarte intens, electronii sunt supuși la forțe electrice foarte mari care înving forțele de interacțiune dintre electroni și nucleu, smulgând electroni de pe orbitele atomilor, acești electroni devenind electroni liberi ce se deplasează, în interiorul dielectricului, sub acțiunea câmpului electric. În această situație, dielectricul și-a pierdut calitatea de izolant, adică a fost străpuns.

Se numește rigiditate dielectrică a unui mediu izolant intensitatea câmpului electric minimă de la care începe străpungerea dielectricului în punctul considerat.

Unitatea de măsură pentru rigiditatea dielectrică este kV/cm.