Fluxul câmpului electric în vid

Fluxul câmpului electric în vid

1.5.1 Fluxul electric

Se consideră un câmp electric și o suprafață S limitată de o curbă oarecare, aflată în câmp. Notăm cu a unghiul format de vectorul câmp electric în vid și normala pozitivă a suprafeței. Componenta normală a intensității câmpului pe elementul de suprafață dS este E_n = E cosa

Se numește fluxul vectorului intensității câmpului electric prin suprafața S integrala de suprafață a produselor dintre elementele de suprafață și componentele vectorului câmp, normale pe aceste elemente:

.

Notând cu d un vector de modul egal cu suprafața dS și având sensul normalei , expresia fluxului devine:

(1.16)

unde este produsul scalar al vectorilor și d.

1.5.2. Unghiul solid

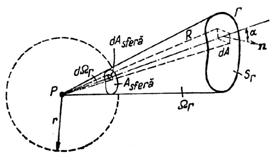
Unghiul solid este o mărime geometrică care caracterizează deschiderea unui con sub care se vede un contur G dintr-un punct P exterior conturului. Unghiul solid se definește ca fiind raportul dintre aria interceptată de generatoarele arcului pe o suprafață sferică de rază R și pătratul acestei raze. (fig.1.5)

Fig. 1.5

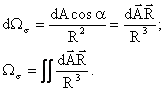(1.17)

Dacă suprafața este o suprafață închisă care conține punctul P în interior, atunci:

. (1.18)

Dacă suprafața este un plan infinit, atunci:

. (1.19)

1.5.2. Teorema lui Gauss

Conform acestei teoreme fluxul vectorului intensității câmpului electric printr-o suprafață închisă dusă în vid, este egal cu raportul dintre sarcina electrică aflată în interiorul suprafeței și permitivitatea vidului:

. (1.20)

Vom demonstra această teoremă în două cazuri particulare:

a) sarcina punctiformă aflată în interiorul suprafeței

Vectorul câmp electric creat de sarcina electrică fiind:

, (1.21)

fluxul elementar prin aria elementară (fig.1.6) are expresia:

(1.22)

iar fluxul total va fi:

. (1.23)

Acest flux rămâne constant chiar dacă liniile de forță intersectează suprafața de mai multe ori, deoarece fluxul lui E₁ și E₂ se anulează, fiind egale și de semne contrare.

b) sarcina punctiformă aflată în exteriorul suprafeței S

În acest caz, un con de linii de forță intersectează suprafața de un număr par de ori și fluxurile se anulează două câte două (Fig. 1.7):

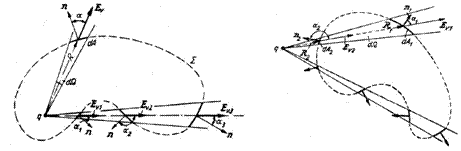
	Fig. 1.6		Fig. 1.7

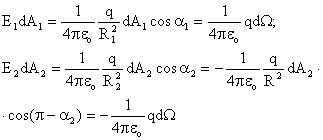
Deci:

(1.24)

Cu ajutorul teoremei lui Gauss se calculează foarte ușor intensitatea câmpului electric când forma liniilor de câmp este cunoscută și prezintă simetrie.