Exemple subiecte de examen la Metode Numerice

Exemple subiecte de examen la Metode Numerice

Gabriela Ciuprina

17 ianuarie 2008

TIP 1 - pseudocoduri, declaratii, ordine de complexitate, variante imbunatatite

Fie urmatorul pseudocod

Scrieti declaratii posibile pentru variabilele care apar

Estimati ordinul de complexitate dpdv al timpului de calcul

Estimati ordinul de complexitate dpdv al necesarului de memorie

Scrieti formula matematica de calcul a rezultatului s, in functie de datele problemei

Propuneti o varianta imbunatatita a acestui cod

Obs. Operatia elementara considerata pentru rezolvarea punctului 2 este evaluarea functiei f (la varianta 1) si evaluarea functiei trigonometrice (la varianta 2). Aceasta se considera ca dureaza mult mai mult decat orice opera 252w227c tie algebrica.

rez = 0

pentru i = 1,n

term = p + f(b_i)

term = term*f(a)

rez = rez + term

p = 1

pentru i = 1,n

t = sin(a_i) + c

t = t*bi

s = 0

pentru k = 1,n

s = s + cos(d_k)

t = t*s

p = p*t

TIP 2 - Calcule cu intervale

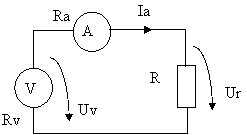
Pentru masurarea rezistentei unui rezistor se utilizeaza metoda ampermetrului si voltmetrului in conexiune amonte cf. schemei de mai jos.

Rezistentele aparatelor sunt Ra = 1ohm, respectiv Rv = 100kOhmi.

Tinand cont ca precizia ampermetrului este de 1%, iar cea a voltmetrului este de 2%, sa se determine valoarea rezistentei R in doua cazuri:

1. Se utilizeaza relatia aproximativa R = Uv/Ia
2. Se utilizeaza relatia exacta R = Uv/Ia - Ra

Indicatiile aparatelor sunt: Ia = A, Uv = V

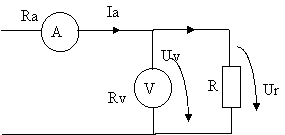
Pentru masurarea rezistentei unui rezistor se utilizeaza metoda ampermetrului si voltmetrului in conexiune aval cf. schemei de mai jos.

Rezistentele aparatelor sunt Ra = 1ohm, respectiv Rv = 100kOhmi.

Tinand cont ca precizia ampermetrului este de 1%, iar cea a voltmetrului este de 2%, sa se determine valoarea rezistentei R si precizia ei in doua cazuri:

3. Se utilizeaza relatia aproximativa R = Uv/Ia
4. Se utilizeaza relatia exacta R = 1/(Ia/Uv - 1/Rv)

Indicatiile aparatelor sunt: Ia .. A, Uv = ... V

TIP 3 - Gauss

Enunt:

Sa se rezolve cu metoda Gauss fara pivotare urmatoarele 2 sisteme.

Care este ordinul de complexitate (timp si memorie) pentru metoda Gauss fara pivotare?

1 a) 2*x + 3*y - 4*z = 20

4*x + 4*y + z = 9

8*x - y + 2*z = 0

1.b) 2*x + 3*y - 4*z = 20

4*x + 6*y-8*z = 40

8*x - y + 2*z = 0

1.a) x + 2*y - 3*z = 7

3*x - 4*y + 2*z = -11

4*x + 2*y - 5*z = 8

1.b)   x + 2*y - 3*z = 7

3*x - 4*y + 2*z = -11

6*x - 8*y +4*z = -22

TIP 4 . Factorizare LU

Fie sistemul algebric liniar

3x + 7y - 2z = 5

6x - 10y + z = -23

-9x-21y+2z = -27

Care sunt factorii L si U ai matricei coeficientilor?

Sa se rezolve sistemul folosind metoda factorizarii LU

TIP 5 - Metode iterative

Varianta 1

Fie sistemul algebric liniar

3x + 7y - 2z = 5

6x - 10y + z = -23

-9x-21y+2z = -27

Daca x₀= 0, z₀= 0, x₀= 0, calculati prima iteratie Jacobi si prima iteratie Gauss Seidel.

Varianta 2

Fie sistemul

x - 2y = -2

-3x + 2y = -6

In cazul rezolvarii lui iterative cu metoda Jacobi / Gauss-Seidel, daca initializarea este nula, cat este solutia la primul pas. Reprezentati geometric procesul iterativ si indicati pe figura pozitia celei de a doua iteratii. Comentati convergenta. Ce se intampla daca se schimba ordinea ecuatiilor?

TIP6 - Structuri de date, matrice asamblate pentru circuite rezistive liniare

Se va da un circuit rezistiv liniar (cu rezistente si surse de tensiune).

Sa se scrie structurile de date ce descriu acest circuit

Exemplificati modul de asamblare al matricei coeficientilor si vectorul termenilor liberi. Comentati dimensiunea sistemului asamblat fata de dimensiunea sistemului supus rezolvarii.

TIP 7 - Interpolari, derivare numerica

Varianta 1

Fie tabelul de valori

sau

Care sunt polinoamele Lagrange de ordinul doi asociate diviziunii pe x?

Deduceti expresia polinomului de interpolare de grad doi (folosind metoda Lagrange). Comentati rezultatul

Deduceti expresia polinomului de interpolare de grad doi (folosind metoda clasica).

Deduceti expresia polinomului de interpolare de grad doi (folosind metoda Newton, calculand mai intai tabelul diferentelor divizate).

Calculati y'(0) folosind trei formule diferite de derivare numerice (precizati formulele, numele lor si ordinul, si efectuati si calculul numeric propriu-zis)

Varianta 2

Fie tabelul de valori

Sa se scrie algoritmul complet al unui program care calculeaza derivata numerica f'(5).

Varianta 3

a) Sa se deduca formula diferentelor centrate de ordin 4.

b) Sa se deduca formula diferentelor regresive de ordin 3.

Varianta 4

Fie tabelul de valori

Sa se calculeze polimonul de interpolare liniara pe portiuni.

TIP8 - Aproximari (regresii) liniare

Fie tabelul de valori

Care este expresia care se minimizeaza in metoda celor mai mici patrate, atunci cand se calculeaza regresia liniara a datelor din tabel?

Calculati regresia liniara pentru datele din tabel.

TIP9 - Integrare numerica

Varianta 1

Fie tabelul de valori

Calculati 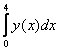folosind metoda trapezelor si metoda Simson.

Varianta 2

Fie y(x) = x*x - 2

Calculati 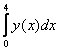folosind metoda trapezelor si metoda Simson, folosind o retea de discretizare uniforma cu 3 puncte in intervalul [0,4]. Calculati erorile relative fata de valoarea exacta. Comentati rezultatul.

TIP 10 - Ecuatii algebrice neliniare

Varianta 1

Fie ecuatia x^2 = 3, unde x este in [0,3].

Ilustrati grafic metoda bisectiei. Calculati primele doua iteratii

Ilustrati grafic metoda Newton daca initializarea este 1.5. Calculati prima iteratie

Ilustrati grafic metoda Newton daca initializarea este 0. Comentati

Varianta 2

Sa se scrie algoritmul complet pentru rezolvarea ecuatiei e^x=2, x apartine intervalului [0,5], cu metoda bisectiei.

TIP 11 - Sisteme de ecuatii algebrice neliniare - aplicatii pe circuite

Se va da un circuit rezistiv neliniar (contine surse de tensiune, rezistoare si diode).

Sa se scrie structurile de date ce descriu acest circuit

TIP12- Ecuatii diferentiale - aplicatii pe circuite

Se da un circuit liniar in regim tranzitoriu (tranzitia se face de la o stare stationara la alta stare statioara - probleme cu intrerupatoare sau comutatoare)

a)      Care sunt structurile de date ce descriu circuitul in regim tranzitoriu

b)      Care sunt conditiile initiale (curentii prin bobine si tensiunile la bornele condensatoarelor)

c)      Desenati circuitul discretizat la primul pas de timp t₁ = h

d)      Calculati noile valori ale variabilelor de stare (curentii prin bobine si tens pe condensatoare), necesare urmatoarei iteratii.

TIP - OBLIGATORIU (subiect de 20 pct din 40 posibile)

Sa se scrie pseudocodul complet al unui algoritm pentru rezolvarea unui circuit

rezistiv liniar

sau

rezistiv neliniar

sau

liniar in regim tranzitoriu

Diferite cerinte sunt posibile (solvere diferite pentru sistemul algebric liniar, folosirea sau nu a zeroului masinii pentru oprirea iteratiilor, impunerea numarului maxim de iteratii a.i. rezolvarea sa dureze cel mult cat Gauss, etc)

Succes!