Calculul integral pentru functiile pare si impare generalizate

Calculul integral pentru functiile pare si impare generalizate

VI.I. Asupra calculului integral pentru functiile pare si impare.

Propozitia 1.

Fie

o functie continua.Atunci:

.

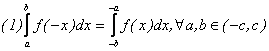In particular,

.

(2) f este para, daca si numai daca ,

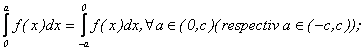
(3) f este impara, daca si numai daca,

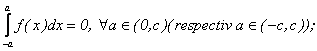
(4)Daca, in plus, f este para, atunci

;

(5)(i) daca f este para, atunci

;

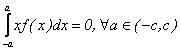(ii) daca f este impara, atunci

;

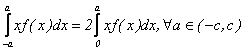(iii) daca f este arbitrara, atunci

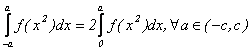
Si

;

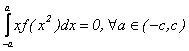Demonstratie:

Fie fixati; facand substitutia x=-t, obtinem c.c.t.d.

Daca f este para, si deci:

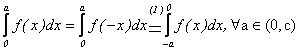
Reciproc, sa presupunem ca

.

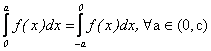Atunci:

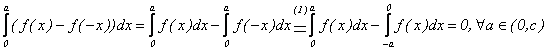
Rezulta ca

Daca si deci adica f este para.

(3)Daca f este impara , si deci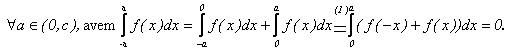

Reciproc, fie fixati. Conform ipotezei, avem:

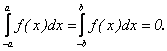
Dar,

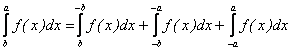si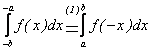

Rezulta ca

,

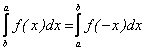deci

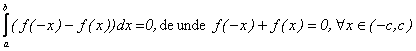
; prin urmare f este impara.

Daca f este para, avem si deci: .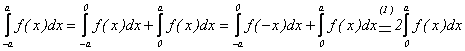

(i) Daca f este para, atunci functia este impara, si deci .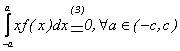

(ii) Analog ca in (i)

(iii) Rezulta imediat din (i) si (ii), tinand seama de faptul ca, functia este para (respectiv impara).

Propozitia 2.

Sa se arate ca o functie , continua este impara, daca si numai daca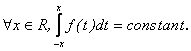

Demonstratie:

f fiind continua, admite primitive; fie F o primitiva a sa; rezulta ca :

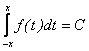
daca si numai daca , prin derivare, daca si numai daca , adica f este impara .

Reciproc, daca f este impara implica .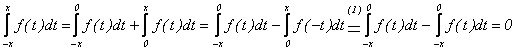

VI.II. Asupra calculului integral pentru functiile pare si impare generalizate.

Definitie. Functia se numeste a-para, daca respectiv a-impara, daca .

Propozitia II.1.

Fie continua, cu proprietatea ca: ; atunci :

;

.

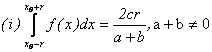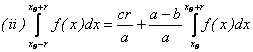Demonstratie:

Consideram

este continua , putem aplica schimbarea de variabila :

;

Rezulta ca

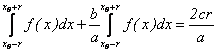
si deci

.

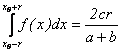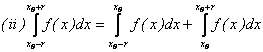. Dar ;

rezulta ca

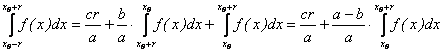
Propozitia II.2.

(i)          Daca  este continua atunci :

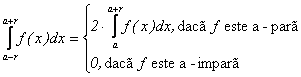
(ii)Produsul (catul) a doua functii de a-paritati diferite este o functie a-impara si produsul (catul) a doua functii de aceeasi a-paritate este o functie a-para.

Demonstratie:

(i)          Daca f este a-para, atunci ; deci in II.1. punand a=1, b=-1, c=0, x₀=a si conform II.1.(ii) rezulta ca :

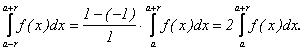
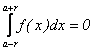Daca f este a-impara, atunci, si punand in II.1.(ii) a=b=1, c=0, rezulta ca .

; rezulta ca si analog , ; rezulta ca si sunt a-pare, analog aratandu-se si restul.

Propozitia II.3.

Pentru orice functie , exista o functie a-para si o functie a-impara, astfel incat .

Demonstratie:

;

rezulta ca rezulta ca

Propozitia II.4.

Daca sunt integrabile si f este a-para, atunci:

.

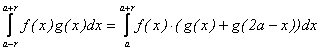Demonstratie:

Din II.3. rezulta ca , unde g₁ este a-para si g₂ este a-impara. Rezulta

Propozitia II.5.

Fie integrabile si f este a-impara. Atunci:

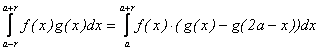
Demonstratie:

Se demonstreza analog cu propozitia II.4 utilizand II.2. si II.3.

Bibliografie

V. Arsinte, Probleme elementare de calcul integral, Editura Universitatii Bucuresti, 1995.

VII. Calculul  integral in cazul functiilor periodice

Propozitia 1. Fie o functie continua. Atunci avem:

a)      este periodica de perioada T, daca si numai daca, 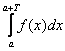= c(constant)

a;

b)      Urmatoarele afirmatii sunt echivalente:

(i)          Orice primitiva a lui , este periodica de perioada T;

(ii)        f este periodica, de perioada T;

(iii)       ,

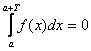Demonstratie:

a) . Din ipoteza, 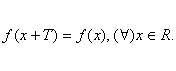Avem:

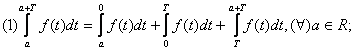
Facand in ultima integrala, schimbarea de variabila t=y+t, , obtinem:

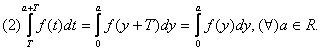
Din (1) si (2) rezulta: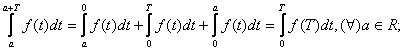

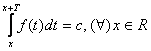Presupunem ca si fie F o primitiva a lui .

Atunci , si deci prin derivare obtinem:

de unde rezulta ca este periodica de perioada T.

b)  (i) (ii) Mai intai, observam ca , orice primitiva a lui este periodica de perioada T, daca si numai daca, exista o primitiva a lui , periodica, de perioada T, daca si numai daca, functia 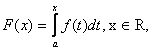este periodica de perioada T.

(ii)(i). Daca f este periodica, de perioada T, avem: si deci, exista un ,

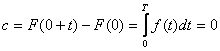astfel incat Atunci , deci , si deci F este periodica, de perioada T.

(ii)(iii). Rezulta din a).

(i)(iii). Daca (i) este adevarata, atunci F este periodica, de perioada T, si avem: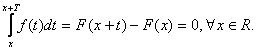

(iii). Din 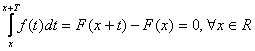si deci F este periodica, de perioada T.

Bibliografie

V. Arsinte, Probleme elementare de calcul integral, Editura Universitatii Bucuresti, 1995.