Campul scalar

Câmpul scalar

1. Câmpul scalar si suprafetele de nivel

Definitie: Fie un domeniu D din spatiu(fig.1). Acestui domeniu îi atribuim o functie scalara f cu o valoare numerica bine determinata în fiecare punct. Vom numi o astfel de functie, functie de punct în domeniul considerat, iar domeniul D îl vom numi câmp scalar al functiei f.

Fig.1. Camp scalar si suprafete de nivel

Daca ne referim la coordonate carteziene, atunci pozitia fiecarui punct va fi determinata de coordonatele lui x, y si z. Prin urmare, putem caracteriza functia f drept o functie scalara oarecare de coordonatele x, y, z,

f(x, y, z).   (1)

În general, când nu ne vom referi la un anumit sistem de coordonate, vom scrie:

f(M) sau f( r)   (2)

Aceste notatii ne indica faptul ca f depinde de pozitia punctului M.

Domeniul D poate ocupa o parte limitata a spatiului sau întreg spatiul. În prima situatie trebuie precizate în fiecare caz concret suprafetele care-l limiteaza. În particular, domeniul D poate degenera într-un plan(sau o portiune din plan). În acest caz vom spune ca avem un câmp scalar plan.

Notiunea de câmp scalar este foarte raspândita în fizica si în stiintele matematice.

Sa consideram astfel domeniul D care reprezinta un volum oarecare ocupat de un corp fizic la un anumit regim termic. Temperatura T are o valoare bine determinata în fiecare punct al corpului.

T(x, y, z) (3)

Ansamblul valorilor lui T în toate punctele volumului considerat constituie câmpul scalar al temperaturilor. Daca vom întelege prin domeniul D volumul unui solid oarecare, atunci putem considera densitatea materialului ρ(x, y, z) în fiecare punct al solidului. Obtinem câmpul scalar al densitatilor.

Sa consideram un exemplu din teoria electricitatii. Un câmp electrostatic este produs de sarcina punctiforma q, situata într-un punct oarecare A. Fie M punctul considerat al acestui câmp, situat la distanta r de sarcina. Fiecarui punct M îi putem atribui o marime scalara V egala cu

  (4)

Acestei marimi scalare îi vom spune potentialul câmpului scalar în punctul dat. Numeric, aceasta marime este egala cu lucrul mecanic pe care l-ar efectua fortele câmpului deplasând o sarcina unitara +1 din acest punct la infinit. Totalitatea valorilor functiei V în toate punctele spatiului constituie un câmp scalar oarecare numit câmp scalar al potentialului. Daca acest câmp electrostatic va fi produs de câteva sarcini punctiforme, potentialul lui într-un punct arbitrar se exprima prin formula:

(5)

unde r_k reprezinta distanta punctului considerat M de la sarcina q_k.

2. Metode de cercetare a câmpurilor scalare

2.1. Trasarea suprafetelor de nivel

Prima metoda si cea mai simpla consta în trasarea suprafetelor de nivel sau a suprafetelor izostatice. Sa atribuim scalarului f o valoare numerica oarecare C

f(x, y, z) = C   (6)

si sa cautam locul geometric al tuturor punctelor regiunii în care functia primeste aceasta valoare data.

Vom obtine, în general, o suprafata S bine determinata, stiind faptul ca locul geometric al punctelor ale caror coordonate satisfac o ecuatie de forma (6) reprezinta o suprafata. Aceasta suprafata se numeste suprafata izostatica sau suprafata de nivel. Relatia (6) reprezinta ecuatia suprafetei de nivel în coordonate carteziene.

Atribuim constantei C diferite valori numerice

C₀+ C₁ = C₀ + ΔC₀; C₂ = C₁ + ΔC₁; .   (7)

si vom obtine o familie de suprafete de nivel.

În inginerie aceste suprafete poarta nume speciale. În electrostatica li se spune suprafete echipotentiale(potential constant), în teoria caldurii li se spune izoterme etc.

În cazul particular al unui câmp scalar plan, vom obtine linii de nivel definite de ecuatia f(x, y) = C. De exemplu, în meteorologie se traseaza pe harti linii de temperatura constanta (izoterme) si de presiune constanta (izobare).

În practica liniile sau suprafetele de nivel se traseaza la cresteri egale una de alta, adica

ΔC₀ = ΔC₁ = ΔC₂ = .=ΔC   (8)

Imaginea suprafetelor trasate în câmpul respectiv descrie structura acestuia. Aceasta imagine ne permite sa observam directiile în care functia creste, scade sau pastreaza o valoare constanta. Putem face si aprecieri cantitative astfel încât acolo unde suprafetele de nivel sunt mai apropiate unele de altele si în care "densitatea" lor este mare le corespunde o variatie mai mare a functiei f dintre doua puncte vecine, si invers.

Observatie: Daca f reprezinta o functie univoca, atunci suprafetele de nivel nu se intersecteaza.

Exemplul 1. Se cere sa se cerceteze suprafetele echipotentiale ale câmpului electrostatic produs de o sarcina punctiforma q.

Solutie: Fie q>0. Egalam functia scalara (3) cu o constanta C

  (9)

Relatia (9) reprezinta ecuatia unei suprafete echipotentiale, de forma

    (10)

Expresia de mai sus reprezinta locul geometric al punctelor egal departate de punctul dat A, unde este situata sarcina q(fig.2)

Fig.2. Suprafete echipotentiale în câmp electrostatic

S-a obtinut ecuatia unei suprafete sferice cu centrul în punctul A si cu raza egala cu (fig.2). Daca modificam parametrul C, atunci obtinem o familie de suprafete sferice concentrice. Raza r descreste pe masura ce creste C, deci functia creste atunci când ne apropiem de punctul A, rezulta ca suprafetele de nivel devin mai dese pe masura ce ne apropiem de punctul A.

Exemplul 2.

În planul xOy sunt date doua puncte F₁ si F₂. Distanta dintre ele este egala cu 2c(fig.3). Fiecarui punct M al planului îi atribuim o marime scalara

r₁ +r₂   (11)

Valoarea numerica a acestei functii scalare este egala cu suma distantelor dintre punctele date F₁ si F₂.

Se cere sa se determine liniile de nivel ale functiei r₁+r₂.

Fig. 3. Liniile de nivel ale functiei r₁+r₂

Solutie:

Egalam functia cu o constanta si obtinem:

f = r₁+ r₂ = C   (12)

Obtinem astfel ecuatia unei familii de elipse omofocale cu focarele în punctele F₁ si F₂(fig.3).

3. Derivata unei functii scalare în raport cu o directie data. Gradientul

Consideram dat un câmp scalar al unei functii oarecare f si punctul M în interiorul lui. Valoarea functiei în acest punct va fi f(M). Ne deplasam din punctul M într-un punct vecin M₁ situat la o distanta infinit mica Δs pe o directie paralela cu versorul dat s(fig.4).

Fig.4. Ilustrarea obtinerii gradientului

Functia va lua în punctul M₁ o valoare oarecare f(M₁). Diferenta f(M₁) - f(M) = Δf reprezinta cresterea functiei corespunzatoare deplasarii Δs. Calculam raportul dintre cresterea functiei si deplasarea Δs.

  (13)

Acest raport reprezinta viteza medie de variatie a functiei pe unitatea de lungime a drumului parcurs în directia data. Facem pe Δs sa tinda catre zero paralel cu versorul s. Punctul M₁ se va apropia de punctul M de-a lungul unei drepte paralele cu s. În general, raportul va tinde catre o limita determinata.

  (14)

Aceasta limita este derivata lui f în punctul M în raport cu directia s si o notam simbolic cu .

Astfel, prin definitie

  (15)

Simbolul ∂ indica faptul ca functia poate avea în punctul M mai multe derivate în raport cu toate directiile asociate cu M.

4. Gradientul în coordonate carteziene

Alegem ca sistem de referinta al câmpului scalar dat sistemul de coordonate rectangulare Oxyz. În acest caz, deplasându-ne de la punctul M(x, y, z) pâna la punctul M₁(x+Δx, y+Δy, z+Δz) functia va creste cu

(16)

Introducem diferentiala totala

(17)

Obtinem:

  (18)

Dar,

  (19)

unde α, β, γ sunt unghiurile versorului s cu axele de coordonate.

Rezulta:

(20)

În concluzie

(21)

Expresia de mai sus reprezinta valoarea derivatei în coordonate carteziene, în punctul M, în raport cu directia s.

Gradientul functiei scalare f este dat de expresia:

  (22)

Teorema: Într-un punct dat derivata unei functii scalare f în raport cu o directie oarecare s este egala cu proiectia gradientului acestei functii în punctul considerat pe directia data.

Valoarea gradientului este data de expresia:

  (23)

Gradientul unei functii într-un punct oarecare reprezinta un vector egal în valoare numerica cu maximul vitezei de variatie a functiei f în punctul considerat si a carui directie coincide cu directia celei mai rapide dintre variatii.

Gradientul unui câmp scalar reprezinta un invariant al câmpului. Marimea si directia lui depind numai de proprietatile functiei f, fiind independente de alegerea sistemului de referinta.

5. Gradientul si suprafetele de nivel

1. Gradientul este perpendicular pe suprafata de nivel

Consideram o suprafata de nivel S care trece prin punctul M si satisface ecuatia

f = C   (24)

Vom arata ca gradientul este perpendicular pe aceasta suprafata.

Fie MT o directie oarecarec tangenta la suprafata de nivel în punctul considerat(fig.4) si situata în planul P tangent la suprafata de nivel. Derivata în raport cu aceasta directie este nula, deoarece functia este constanta pe suprafata de nivel. Pe de alta parte, derivatele trebuie sa fie egale cu proiectia gradientului pe aceasta directie.

Rezulta ca

G_t = 0   (25)

adica gradientul este perpendicular pe orice dreapta dusa în planul tangent prin punctul M. Prin aceasta gradientul este perpendicular pe planul tangent. Deci gradientul este orientat de-a lungul normalei la suprafata de nivel.

Fig.5: Constructia gradientului într-un punct

al unei suprafete de nivel

2. Gradientul este orientat în sensul cresterii functiei

Construim în punctul M versorul normalei(fig.5) n pe suparafata f = C si orientat în sensul cresterii lui f. Presupunem ca acest vector intersecteaza o suprafata infinit vecina

f = C + ΔC = C₁; ΔC > 0 (26)

în punctul M₁ si ca MM₁ = Δ n.

În acest caz,

  (27)

Consideram semnul ± deoarece nu stim înca daca unghiul dintre G si n este 0^o sau 180⁰. Membrul stâng al egalitatii de mai sus este pozitiv deoarece ΔC > 0. Prin urmare, trebuie ca si membrul drept sa fie pozitiv. Acest lucru ne arata ca unghiul dintre gradientul G si n este nul si deci gradientul este orientat în sensul cresterii functiei.

Rezulta

  (28)

Corolar.

Cele doua proprietati de mai sus ne permit sa dam o definitie a gradientului. Gradientul unei functii scalare f într-un punct oarecare poate fi definit ca vectorul normal la suprafata de nivel în punctul considerat. Gradientul este orientat în sensul cresterii functiei si este egal în valoare numerica cu derivata ei în raport cu normala pe suprafata

  (29)

Acest lucru confirma din nou faptul ca gradientul este independent de sistemul de coordonate, adica are un caracter invariant.

Problema:

Campul electrostatic este produs de sarcina punctiforma q situata în punctul A(fig.2) Se cere sa se afle gradientul potentialului

    (30)

Solutie: Alegem sistemul de coordonate carteziene rectangulare cu originea în punctul A. În acest caz, pentru punctul considerat M putem scrie:

  (31)

Determinam proiectiile gradientului pe axele de coordonate

  (32)

Din expresia lui r avem

  (33)

Analog, obtinem:

  (34)

Componentele gradientului pe cele trei axe sunt:

(35)

Înmultim egalitatile de mai sus cu si le adunam

(36)

În expresia de mai sus suma din paranteza reprezinta vectorul de pozitie al punctului considerat, si putem scrie

(37)

Cunoastem ca într-un câmp electrostatic vectorul intensitate E este egal în valoare numerica cu gradientul potentialului V si este orientat în partea opusa acestui gradient

  (38)

Rezulta ca

E = -grad V   (39)

Egalitatea de mai sus se descompune în trei egalitati analitice

(40)

Într-un câmp electrostatic proiectiile vectorului E pe axele sistemului rectangular de coordonate sunt egale cu derivatele partiale ale functiei V în raport cu x, y si z, luate cu semnul schimbat.

6. Exprimarea simbolica a gradientului.

Operatorul lui Hamilton sau operatorul nabla

Consideram expresia geadientului unei functii f în coordonate carteziene

  (41)

În expresia de mai sus consideram, în mod conventional, pe f ca factor

(42)

Expresia din paranteza o notam cu simbolul nabla( )

(43)

Cu aceasta notatie expresia gradientului are forma:

grad f = f  (44)

Simbolul se numeste operatorul lui Hamilton sau nabla. Expresia de mai sus se numeste expresia simbolica a gradientului.

Problema:

Se cere sa se gaseasca gradientul sumei a doua functii scalare f + h .

Solutie:

Calculam derivatele partiale ale sumei de functii în raport cu x, y si z

(45)

Înmultim relatiile de mai sus cu , le adunam si obtinem:

grad(f + h) = grad f + grad h (46)

sau, în sciere simbolica:

(f + h) = f + h    (47)

Problema:

Se cere sa se deterime gradientul produsului a doua functii scalare f.h

Solutie:

Calculam derivatele partiale ale produsului de functii în raport cu x, y si z

(48)

Înmultim relatiile de mai sus cu versorii si adunam pe coloane.

Obtinem:

grad(f.h) = f.grad h + h.grad f   (49)

sau, în scriere simbolica

(f.h) =f. h+h. f    (50)

Problema:

Se cere sa se calculeze gradientul unei functii scalare compuse

Solutie:

Consideram o functie oarecare F(u) care depinde de u, iar u este functie de x,y, z, u = f(x, y, z).

Calculam derivatele partiale ale functiei F.

(51)

Înmultim relatiile de mai sus cu , le adunam si obtinem:

grad F(u) = F '(u).grad u   (52)

sau, simbolic

F(u) = F'(u). u    (53)

Problema:

Se cere sa se gaseasca gradientul lui r, r fiind distanta punctului M fata de un punct A considerat ca origine(fig.6).

Fig.6.

Alegem ca sistem de referinta al functiei r un sistem de coordonate carteziene rectangulare cu originea într-un punct arbitrar O, diferit de punctul A.

Functia r are expresia:

(54)

Derivam functia r în raport cu x si obtinem:

(55)

Analog obtinem:

(56)

Înmultim relatiile de mai sus cu , le adunam si obtinem:

(57)

Problema:

Consideram un câmp electrostatic produs de n sarcini electrice punctiforme q₁, q₂, .,q_n. Se cere sa se determine gradientul functiei

(58)

unde r_k sunt distantele dintre punctul considerat M si punctele A_k în care sunt situate sarcinile punctiforme.

Solutie:

Folosim formulele de mai sus si obtinem:

(59)

7. Câmpul vectorial. Linii vectoriale.

Consideram în spatiu un domeniu D(fig.7). Fiecarui punct M îi vom atribui un vector cu o valoare numerica si o orientare bine determinate. Vom numi pe functie vectoriala de punct în domeniul considerat, adica

= (M)    (60)

Domeniul D este câmpul vectorial al vectorului . Pentru a definin un câmp vectorial trebuie sa indicam legea conform careia putem determina în orice punct M al domeniului considerat atât marimea cât si orientarea vectorului.

Fig.7: Câmp vectorial

În coordonate carteziene rectangulare, unde

(61)

trebuie sa cunoastem cele trei proiectii ale vectorului

a_x = a_x(x, y, z); a_y = a_y(x, y, z); a_z = a_z(x, y, z)  (62)

sub forma a trei functii scalare de coordonatele x, y, z. ale punctului M.

Exista, în fizica, multe câmpuri vectoriale, de exemplu: câmpul electrostatic al unor sarcini punctiforme, câmpul magnetic al unui conductor parcurs de curent, câmpul gradientului unei functii scalare oarecare f.

În mecanica exista câmpuri vectoriale ale vitezelor si acceleratiilor unui solid într-un moment oarecare, fiecarui punct al solidului în miscare fiindu-i atribuite un vector viteza si un vector acceleratie.

În cele ce urmeaza ne vom ocupa de câmpuri vectoriale în general. În particular, când vectorul reprezinta o forta vom spune ca avem un câmp de forte.

Exista multe metode de creare a câmpurilor vectoriale întâlnite în teoria electricitatii, a magnetismului, a elasticitatii, mecanica fluidelor, teoria potentialului etc.

7.1. Linii vectoriale

Prima metoda de studiu a câmpurilor vectoriale consta din trasarea asa numitelor linii vectoriale. Vectorul câmp este tangent la linia vectoriala în fiecare punct al ei(fig.7) În cazul particular al câmpurilor de forte, liniile vectoriale sunt numite linii de forta, în mecanica fluidelor se numesc linii de curent etc.

Linia de forta a unui câmp electrostatic reprezinta linia de-a lungul careia s-ar misca o sarcina libera +1, fara viteza initiala, ea fiind doar sub actiunea fortelor câmpului.

Determinam ecuatia diferentiala a liniei vectoriale.

Observam în figura 8 vectorul de pozitie al punctului curent M, care apartine acestei linii si satisface relatia

=(s)   (63)

care reprezinta ecuatia sub forma vectoriala.

Fig.8. Linii vectoriale

Punem conditia ca vectorul câmp sa coincida în fiecare punct M cu versorul tangent 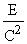. Este suficient sa punem conditia ca si sa fie paraleli, deoarece au un punct comun M, obtinem:

(64)

Relatia de mai sus este chiar ecuatia cautata. Pentru a o transpune în forma analitica folosim faptul ca proiectiile vectorilor paraleli sunt proportionale între ele.

Obtinem:

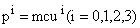(65)

sau

(66)

Am obtinut un sistem de ecuatii diferentiale scrise sub forma de proportii. Prin urmare, problema determinarii liniilor vectoriale se reduce la integrarea unui sistem de ecuatii diferentiale de forma de mai sus.

Presupunem ca am gasit doua integrale independente ale sistemului de mai sus

f₁(x, y, z) = C₁

f₂(x, y, z) = C₂     (67)

Ansamblul celor doua ecuatii va determina linia vectoriala, aceasta constituind intersectia a doua suprafete. Modificând arbitrar parametrii C₁ si C₂, vom obtine o familie de linii vectoriale care depind de doi parametri. În cazul general, integrarea sistemului de ecuatii diferentiale de mai sus este uneori foarte dificila. De aceea, în practica, se obisnuieste mai ales în cazul câmpurilor plane si paralele, sa se traseze liniile prin metode grafice aproximative.

7.2. Densitatea liniilor vectoriale

Deoarece putem lua drept punct initial orice punct A, pentru trasarea liniei vectoriale, înseamna ca numarul liniilor este infinit si din punct de vedere teoretic, ele pot acoperi întregul domeniu D în mod uniform. Câmpul vectorial are o densitate diferita a liniilor vectoriale în diferitele sale puncte; densitatea este mai mare acolo unde a este mai mare si invers. Daca vectorul are aceeasi marime, orientare si sens în toate punctele unui domeniu oarecare, atunci liniile vectoriale vor umple câmpul în mod uniform. Acest câmp se va numi câmp uniform.

Problema:

Intensitatea H a campului lung si rectiliniu în punctele exterioare se determina prin expresiile:

(68)

unde

(69)

Se cere sa se determine liniile vectoriale si forma lor.

Solutie:

Scriem sistemul de ecuatii diferentiale corespunzator problemei noastre

(70)

Deducem ca dz = 0 deoarece numai în acest caz ulimul raport poate fi egal cu primele doua.

Rezulta

z = const. = C₁   (71)

Ecuatia de mai sus reprezinta o familie de plane paralele cu planul xOy, situate la distante corespunzatoare diferitelor valori pe care le ia constanta C₁.

Din primele doua relatii obtinem:

x.dx + y. dy = 0 (72)

sau

  (73)

de unde rezulta:

(74)

Am obtinut o familie de cilindri circulari drepti. Axele lor coincid cu axa z, iar razele sunt determinate de C₂.

Ansamblul ecuatiilor

z = const. = C₁

  (75)

determina liniile vectoriale ca fiind intersectia de plane cu familia de suprafete cilindrice. Liniile reprezinta niste cercuri cu centrele situate pe axa z. Cercurile se afla în plane perpendiculare pe axa conductorului.

Daca am fi studiat proiectiile câmpului magnetic interior

H_x = -2π u y; H_y = 2πux; H_z = 0 (76)

am fi obtinut un sistem de ecuatii diferentiale de forma de mai sus. Prin urmare si liniile vectoriale ale câmpului interior reprezinta niste cercuri.

Problema

Se cere sa se determine divergenta câmpului electrostatic produs de o sarcina punctiforma situata în punctul A(a, b, c).

Solutie:

Expresia intensitatii câmpului electrostatic este

  (77)

unde

  (78)

În acest caz

(79)

Derivatele partiale ale lui E_x, E_y, E_z în functie de x, y, z sunt:

(80)

(81)

(82)

Adunam relatiile de mai sus si obtinem:

(83)

 

Se observa ca numaratorul celei de a doua fractii din relatia de mai sus este chiar r².

Rezulta ca

  (84)

Deci, divergenta câmpului unei singure sarcini electrostatice este nula în toate punctele acestuia.

Problema

Se cere sa se demonstreze ca:

div(a+b) = div a +div b (85)

Solutie:

Se stie ca daca adunam geometric doi vectori, atunci proiectiile lor se vor aduna algebric. Deci

  (86)

si

  (87)

Analog

  (88)

  (89)

Adunam relatiile de mai sus si obtinem:

div(a+b) = div a+ div b   (90)

Problema:

Se cere sa se demonstreze ca

div fa = f.div a + a.grad f   (91)

sau

(f.a)=f a+a f    (92)

unde f este o functie scalara oarecare, iar a este o functie vectoriala de punct.

Solutie:

Daca se înmulteste un vector printr-un scalar, atunci fiecare proiectie a vectorului pe axele de coordonate se va înmulti cu acel scalar.

Deci

  (93)

  (94)

  (95)

Adunam relatiile de mai sus, pe coloane, si obtinem:

(96)

Expresia din paranteza în relatia de mai sus reprezinta tocmai produsul scalar dintre vectorul a si gradientul functiei scalare f.

8. Rotorul câmpului vectorial

Integrala de linie a unui vector

Consideram ca în campul vectorial a am trasat o linie arbitrara pe care am ales doua puncte A si B(fig.9).

Divizam segmentul de linie cuprins între A si B într-un numar mare de puncte M₁, M₂, .M_n-1.

Fixam directia de parcurgere a liniei de la A catre B. Consideram punctele destul de apropiate astfel încât fiecarui element M_kM_k+1 sa-i corespunda un segment. Vom considera aceste elemente ca vectori

.

Fig.9: Rotorul unui câmp vectorial

Construim în fiecare punct M_k un vectorsi calculam suma considerata de-a lungul liniei.

Trecem la limita în relatia de mai sus si obtinem:

  (97)

În cazul particular, când linia AB este închisa, adica atunci când punctul final B coincide cu cel initial A, linia se numeste contur si se noteaza cu C, iar integrala de mai sus se numeste circulatia vectorului a de-a lungul conturului C, si se noteaza cu

  (98)

Se poate da o interpretare fizica a integralei de mai sus, în cazul când vectorul a reprezinta o forta, iar câmpul este un câmp de forte. În acest caz produsul a.dl reprezinta lucrul mecanic al fortei a de-a lungul elementului de drum dl, iar toata integrala reprezinta lucrul mecanic al fortei de-a lungul drumului parcurs AB.

Raportam curba la o origine oarecare O. Se observa din figura 9 ca elementul de drum dl este egal cu cresterea dr a vectorului de pozitie corespunzator punctului M

dl = dr    (99)

si integrala de mai sus se poate scrie sub forma:

  (100)

Descompunem vectorul a si elemenul dr dupa versorii fundamentali ai unui sistem rectangular de coordonate carteziene.

  (101)

În acest caz

  (102)

si

(103)

Rezulta ca efectuarea integralei pe conturul C în coordonate carteziene se reduce la calcularea integralei de forma de mai sus.

Problema:

Se cere sa se calculeze integrala de linie a vectorului

(104)

de-a lungul elipsei din figura 10, în directia indicata de sageata.

Fig.9. Elipsa

Solutie:

Integrala de contur, în acest caz, are forma:

(105)

Consideram ecuatia elipsei sub forma parametrica

x = a.cos t

y = b.sin t   (106)

Obtinem urmatoarea expresie de sub integrala

(107)

Astfel,

(108)

Daca schimbam directia de integrare de-a lungul liniei AB, atunci integrala îsi schimba semnul, fara sa-si schimba valoarea absoluta

(109)

9. Rotorul unui vector

Fie un punct M dintr-un câmp vectorial oarecare a(fig.10). Prin acest punct ducem un element plan infinitezimal de suprafata ΔS de forma arbitrara si marginit de conturul C. Consideram pe contur un sens de parcurs. Vom calcula circulatia vectorului a de-a lungul acestui contur, adica .

Fig.10. Rotorul unui vector

Fie câmpul definit de relatiile:

  (110)

a_x = a _x(x, y, z)

a_y = a _y(x, y, z)   (111)

a_z = a _z(x, y, z)

Integrala de forma

  (112)

se numeste rotorul campului a

Efectuand integralele pe contur se obtine expresia:

(113)

unde cos(n, x), cos(n, x), cos(n, x) sunt cosinusurile directoare ale unghiurilor formate de normala n cu directiile x, y, z.

10. Vectorul rotor

Consideram în punctul M(fig.11) un vector auxiliar W astfel încât proiectiile lui pe axele de coordonate sa fie egale cu valorile corespunzatoare cuprinse în parantezele din relatia de mai sus, adica

  (114)

iar

  (115)

Vectorul W este complet determinat în marime si directie prin aceste egalitati. Îl vom numi vectorul rotor al câmpului în punctul M, sau simplu rotorul vectorului a si-l vom nota conventional prin simbolul rot a astfel încât

(116)

Fig.11: Vectorul rotor

Putem scrie acum

(117)

Relatia de mai sus ne arata ca circulatia vectorului de-a lungul conturului elementului infinitezimal de suprafata S dus prin punctul considerat poate fi exprimata prin fluxul vectorului rotor W prin acest element de suprafata, în directia normalei n legata de directia de parcurgere a conturului.

11. Exemple de rotori frecvent întâlniti în practica

1. Câmpul vitezelor unui solid în rotatie

Consideram un solid care se roteste în jurul unei axe imobile l cu viteza unghiulara ω. Rationamentul ramâne valabil daca vom considera axa l identica cu axa z.

Alegem pe M( r) punctul reprezentativ din câmp, astfel încât

  (118)

Vectorul ω se exprima astfel

  (119)

Vectorul v care reprezinta viteza liniara a punctului M se exprima sub forma:

(120)

sau

    (121)

de unde rezulta:

(122)

Fig.12: Câmpul vitezelor

Calculam acum rotorul vectorului v. Din relatiile date mai sus obtinem:

  (132)

Rezulta

rot v = 2ω   (124)

Rotorul câmpului vitezelor unui solid în rotatie este acelasi în toate punctele câmpului, paralel cu axa de rotatie si egal în marime cu dublul vitezei unghiulare de rotatie.

Exemplul considerat reprezinta cazul cel mai simplu de câmp fizic, care are un vector rotor în fiecare punct al sau. Daca ne imaginam un lichid ce se roteste în jurul unei axe ca un tot, putem întelege notiunea de rotor.

Problema:

Câmpul magnetic al unui conductor rectiliniu infinit lung

Cazul 1. Câmpul exterior.

Câmpul exterior este caracterizat de relatiile:

(125)

unde

(126)

Calculam proiectiile rotorului pe axele de coordonate

  (127)

sau

(128)

Rezulta ca:

rot H_ext= 0    (129)

Deducem ca în câmpul magnetic exterior nu exista rotori. Acesta este un câmp potential.

Cazul 2. Câmpul interior

În cazul câmpului interior avem relatiile:

  H_x = -2π.u.y; H_y = 2.π.u.x; H_z = 0   (130)

unde u reprezinta densitatea de curent.

Rezulta:

(131)

= 2.π.u + 2.π.u = 4 π.u

Deci,

= 4π.u (132)

În câmpul magnetic interior al curentului exista un rotor. Acest câmp este acelasi în toate punctele din interiorul conductorului, este paralel cu sensul curentului si este egal cu 4π.u. Aceasta formula este valabila nu numai pentru un conductor rectiliniu ci în general.

Problema:

Câmpul electrostatic

Consideram câmpul unei singure sarcini punctiforme

(133)

Rezulta:

(134)

Analog se poate arata ca si celelalte doua proiectii sunt nule.

Astfel

rot E = 0    (135)

ceea ce înseamna ca un câmp electrostatic produs de o singura sarcina punctiforma este lipsit de rotor.

12. Câmp rotoric

Consideram un câmp oarecare a. Construim rotorul lui în fiecare punct si obtinem un nou câmp vectorial oarecare, care se numeste câmp rotoric al câmpului dat. Liniile vectoriale ale câmpului rotoric se numesc linii rotorice. De exemplu, pentru câmpul magnetic interior liniile lui rotorice sunt chiar liniile de curent, deoarece rot H este orientat dupa liniile de curent; în cazul câmpului vitezelor unui solid în rotatie, liniile lui rotorice sunt niste drepte paralele cu axa de rotatie.

Un câmp rotoric are o proprietate importanta aceea ca divergenta lui este nula în toate punctele

div rot a = 0    (136)

Aceasta afirmatie poate fi verificata pe cale directa

Într-adevar

  (137)

Deducem ca

  (138)

Calculam derivatele partiale si obtinem:

  (139)

Adunam relatiile de mai sus si obtinem zero, deci afirmatia de mai sus este demonstrata.