Conform teoremei lui Pitagora
obtinem ecuatia cercului r
= (x-c)
+ (y-d) . Daca centrul cercului se afla in origine, atunci c
= d = 0 si cercul are ecuatia x+ y= r.
|
Ecuatia generala a cercului Centrul M(c,d) Raza r |
(x - c) |
|
Ecuatia cercului cu centrul in origine si de raza r |
x |
y P(x,y)
 |
rr
 |
|||
 |
|||
Conform teoremei
cosinusului, 
+ 
- 2
cos (
-) = r
|
Ecuatia cercului de raza r si centru M ( |
|
|
Caz particular |
|
 |
|||
 |
|||
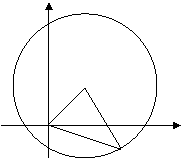
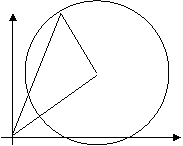
Ecuatiile parametrice, ale cercului
sunt x
= c + r cos t si y = d + r sin t, unde t este unghiul dintre
directia pozitiva a axei Ox si raza trasata
in punctual de pe cerc P(x,y).
|
Ecuatiile parametrice ale cercului de raza r si centru M(c, d) |
x = c + r cos t y = d + r sin t |
 |
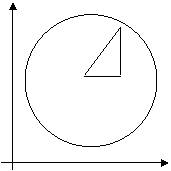
NORMALA CERCULUI y
- d Pentru punctual P (x
,y) care se afla pe cercul (x - c)+ (y - d) = r, -------
x- c
y - y d - y y- d
este directia normalei iar ------- = -------- sau y - y= ------- (x - x) sunt ecuatiile
x
- x c - x x- c
normalei
|
Ecuatia normalei care trece prin punctual P |
y y y x |
|
Ecuatia normalei care trece prin punctual P |
y y y x |
Fie punctual P (x,y) care se afla pe
cercul (x
- c)+ (y - d) = r. Panta
y- d
razei care intersecteaza cercul in punctual
respective este m= ---------- iar
x- c
1 x- c
panta tangentei m
= - ---- = - -------- .
m y- d
Deci, sub forma ecuatiei unei drepte care trece printr-un punct fix si are o
x- c
directie data, ecuatia tangentei va fi y y= -------- (x - x), de unde
y- d
y y- y
- yd + yd = - x x+ x+ cx - c x,
x x+ y y- cx - dy = x+ y- c x - d y.
Adunam in fiecare parte a egalitatii expresia c+ d- c x- d y deoarece P se afla pe cerc, adica (x- c + (y- d) = r, obtinem ecuatia tangentei (x - c) x - (x - c)c + (y - d) y - (y - d)d = r.
|
Ecuatia tangentei in punctul P |
(x - c)( x x x |
 |
|
