Functii hiperbolice
1) Functia ![]() ,
, ![]() , numita ''sinus hiperbolic'' ,
, numita ''sinus hiperbolic'' , 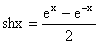 ,
, ![]() .
.
sh
x : R![]() R,
R,
Functia ![]() este impara pentru ca
este impara pentru ca
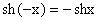 .
.
Graficul este simetric fata de originea axelor.
2) Functia ![]() ,
, ![]() , numita ''cosinus
hiperbolic'' ,
, numita ''cosinus
hiperbolic'' , 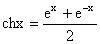 ,
, ![]() ,
,
ch x : R![]()
![]() ,
,
Functia ![]() este o functie para, deoarece
este o functie para, deoarece
![]() .
.
Graficul este simetric fata de Oy si se numeste
curba lantisor,
deoarece da pozitia de echilibru a unui fir omogen, flexibil, inextensibil, supus la actiunea gravitatiei si ale carui capete sunt fixate.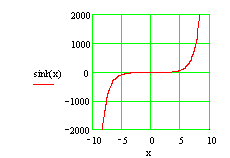
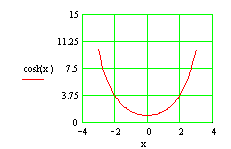
Graficul functiei sh(x) Graficul functiei ch(x)
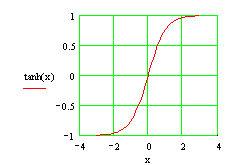
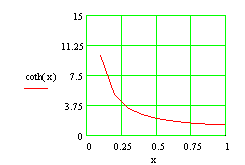
Graficul functiei th x) Graficul functiei cth(x)
3) Functia ![]() ,
, ![]() , numita "tangenta
hiperbolica" este definita de
, numita "tangenta
hiperbolica" este definita de
![]() .
.
4)Functia ![]() ,
, ![]() , numita "cotangenta
hiperbolica" este definita de
, numita "cotangenta
hiperbolica" este definita de
![]() .
.
Proprietatile functiilor hiperbolice. Īnlocuind functiile hiperbolice cu expresiile lor īn functie de exponentiale, se pot demonstra proprietatile:
![]()
![]()
![]()
![]()
si altele analoage cu proprietatile de la functiile circulare.
Inversele functiilor hiperbolice sunt
![]() ,
, ![]() ,
,![]() ,
, ![]() ,
, ![]()
|