Limite de functii

Limite de functii

Notatii: f:D R, D R, a - punct de acumulare a lui D;

II.1. Definitii ale limitei

Definitia II.1.1. , dacã pentru orice vecinãtate V a lui l existã o vecinãtate U a lui a astfel încât " x D U, x a, sã rezulte f(x) V.

Definitia II.1.2. , dacã pentru orice sir (x_n)_{n 0}, x_n D\, având rezultã (criteriul cu siruri);

Definitia II.1.3. , dacã "e>0, d_e >0 astfel încât "x D\ si x - a < d_e rezultã f(x) - l < e;

Definitia II.1.4. , dacã l_s = l_d = l, unde 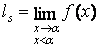si .

II.2. Operatii cu limite de functii

f:D R, g:D R, a - punct de acumulare a lui D, , , l₁,l₂ R;

II.3. Limite tip

, ;

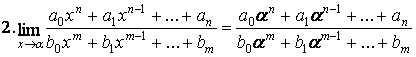
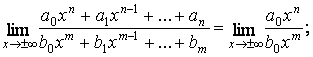
4.

, , dacã a > 1;

, , dacã 0 < a < 1;

si dacã a > 1;

si dacã 0 < a < 1;

6.,

,

,

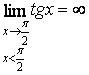7. ,

,

,

,

, ;

8. , , , ;

9.

,

.

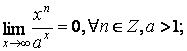
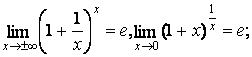
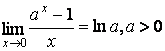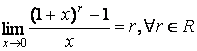II.4. Continuitatea functiilor

Definitia II.4.1. Fie f:D R, x_o D, x_o - punct de acumulare a lui D, f este continuã în x_o, dacã , x_o se numeste punct de continuitate.

Definitia II.4.2. Fie a D, a este punct de discontinuitate de prima spetã dacã existã si sunt finite limitele laterale în a, dar functia nu este continuã în a.

Definitia II.4.3. Fie a D, a este punct de discontinuitate de speta a doua dacã nu este de prima spetã.

Teoremã. Dacã f:I R, I - interval si f continuã pe I, atunci J = f(I) este interval ( o functie continuã pe un interval are proprietatea lui Darboux pe acel interval).