Teste statistice parametrice de comparare

Teste statistice parametrice de comparare

8.2.1 Testul Student de comparare a unei medii cu media teoretica

Uneori cunoastem din literatura de specialitate care este media populatiei din care presupunem ca este extras un lot si dorim sa verificam ipoteza ca esantionul apartine într-adevar populatiei respective.

Sa presupunem ca este media teoretica si sa presupunem ca valorile masurate pentru indivizii din lotul de comparat dau seria statistica: , iar media de esantionare este . Atunci variabila aleatoare , obtinuta dupa formula:

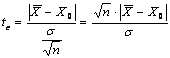
are o repartitie Student cu n-1 grade de libertate. Decizia o vom lua stabilind care este plauzibilitatea ca sa apartina repartitiei Student cu n-1 grade de libertate. Vom cauta limitele dreapta-stânga între care avem cuprinsa 95% sau 99% din aria de sub crba repartitiei Student. Va fi deci suficient sa cauta 343b110d m valoarea lui , sau , data de tabelele statistice pentru t, si sa o comparam cu valoarea lui

O interpretare, a acestui test este deci urmatoarea:

Daca , atunci exista o diferenta semnificativa între media de esantionare si media teoretica

Daca , atunci nu avem motive suficiente pentru a afirma ca exista o diferenta semnificativa între media de esantionare si media teoretica

În figura 8.3, este aratat motivul pentru care comparam cu limita de cuprindere a 95% (99%) din repartitie. Daca este la dreapta acestei limite, este putin probabil sa apartina repartitiei respective si ipoteza H₀ va fi respinsa ca falsa.

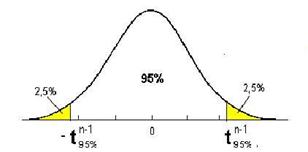
Figura 8.3 Pragul de 95% arata ca valori mai mici decât acest prag sunt plauzibile, iar valori mai mari decât acest prag sunt neplauzibile.

Exemplu practic:

Media esantionare =14,5

Media teoretica =18

Deviatia standard s =12,5

Pragul teoretic t_t = = =1,998

Volumul esantionului n = 84

Deci, calculam valoarea lui t_c :

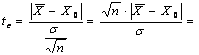
Deoarece t_t < t_c, luam decizia ca diferenta între media de esantionare si media propusa de ipoteza este semnificativa cu pragul de semnificatie de 95%

8.2.2 Testul z pentru compararea unei medii de esantionare cu o medie teoretica când dispersia teoretica este cunoscuta

Este cazul când este cunoscuta si deviatia standard teoretica s. Statistica

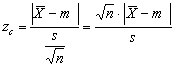
are o distributie care se apropie de distributia normala cu media 0 si abaterea standard 1. În figura 8.4, este aratat modul cum se alege pragul de semnificatie.

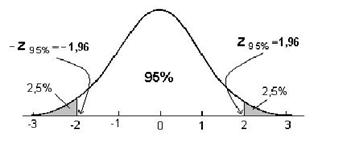
Figura 8.4 Alegerea pragului de semnificatie de 95% pentru testul z de comparare a unei medii de esantionare cu o medie teoretica când dispersia teoretica este cunoscuta

Se observa din figura 8.4, ca testul se bazeaza pe proprietatea distibutiei Gauss standard ca între -1,96 si 1,96 margineste sub curba 95% din aria egala cu 1 sau 100%, marginita de întreaga curba si axa orizontala.

Exemplu de calcul:

Se stie ca pe un lot reprezentativ de pacienti bolnavi de meningita, în anul trecut, s-a obtinut o medie latentei semnalului nervos pe nervul optic, de la retina la lobul occipital, de 105ms iar abaterea standard 8,5ms. Pe un esantion de 54 de pacienti bolnavi de meningita de diverse etiologii, s-a obtinut anul acesta o medie a latentei de 109,3ms. Sa se testeze daca media obtinuta compatibila cu cea de anul trecut la un prag de semnificatie de 95%.

Testarea se face prin calculul lui z_c si compararea cu 1,96.

Deoarece valoarea statisticii întrece pragul theoretic, ipoteza de nul se respinge la pragul de semnificatie de 95%. Media calculata pe esantionul de 54 de pacienti nu este compatibila cu media luata ca teoretica. Explicatia ar putea fi ca lotul de 54 de pacienti luat în studiu nu este reprezentativ, probabil din cauza faptului ca a continut un procent prea mare de tipuri de meningite care modifica latenta.

8.2.3 Testul Student de comparare a mediilor. Cazul esantioanelor mari.

Vom face urmatoarele conventii pentru o mai buna întelegere:

Populatia afectata are media m₁ si abaterea standard s₁, necunoscute.

Populatia neafectata are media m₂ si abaterea standard s₂, necunoscute.

Seria X, extrasa din populatia afectata are volumul n₁, media de esantionare si abaterea standard .

Seria Y, extrasa din populatia neafectata are volumul n₂, media de esantionare si abterea standard .

Ipotezele sub care lucreaza testul sunt:

H₀: m1=m2 Mediile populatiilor din care provin cele doua esantioane sunt aceleasi).

H₁: m1m2 (Mediile populatiilor din care provin cele doua esantioane nu sunt aceleasi).

Testul se bazeaza pe statistica:

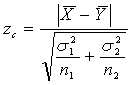
care are o repartitie Gauss standard. Din tabele se ia pragul teoretic de 95% (sau de 99%), care este 1,96 (respectiv, 2,57).

Decizie:

Daca , atunci exista o diferenta semnificativa între mediile de esantionare si .

Daca , atunci nu avem motive suficiente pentru a afirma ca exista o diferenta semnificativa între mediile de esantionare si

Exemplu de calcul:

Determinari ale latentei semnalului nervos pe nervul optic la pacienti cu scleroza multipla si la normali, au aratat urmatoarele:

Ipotezele sunt:

H₀: m1=m2 Mediile populatiilor din care provin cele doua esantioane sunt aceleasi).

H₁: m1m2 (Mediile populatiilor din care provin cele doua esantioane nu sunt aceleasi).

Statistica testului este: 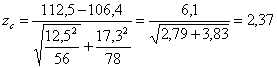. Deoarece este mai mare decât pragul de 1,96, ipoteza de nul se respinge, diferenta între cele doua medii de esantionare este semnificativa la pragul de semnificatie de 95%

8.2.4 Testul Student de comparare a mediilor. Cazul esantioanelor mici si dispersii egale

Fie seriile statistice:

, extras din populatia cu media m₁ si dispersia s² si

, extras din populatia cu media m₂ si dispersia s²

Asadar, avem doua medii de esantionare, si , doua deviatii standard de esantionare si, iar ipotezele pe care le facem sunt:

H₀: m1=m2 Mediile populatiilor din care provin cele doua esantioane sunt aceleasi).

H₁: m1m2 (Mediile populatiilor din care provin cele doua esantioane nu sunt aceleasi).

Daca populatiile sunt de aceeasi dispersie, atunci putem amesteca cele doua esantioane si sa estimam s² prin dispersia de esantionare calculata luând în considerare ambele esantioane:

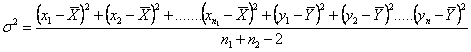
sau cum se poate scrie mai pe scurt:

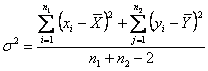
unde la numitor s-a luat n₁+n₂-2, deoarece mediile celor doua loturi sunt doi parametri care se cunosc si deci trebuie sa scadem 2 din numarul de grade de libertate.

Cum din formulele de calcul pentru si , avem:

si

,

vom pune în formula lui la numarator, in locul celor doua sume care se aduna, expresiile si . Deci, formula de calcul a dispersiei comune de esantionare este:

Testul se bazeaza pe statistica

,

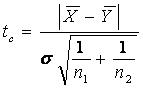care are o distributie Student cu n₁+n₂-2 grade de libertate.

Pentru a alege între ipotezele H0 si H1, ne folosim de aceasta statistica. Decizia este:

Daca , diferenta este semnificativa la pragul de semnificatie de 95%.

Daca , diferenta este nesemnificativa la pragul de semnificatie de 95%.

Sa mai amintim ca am folosit tacit ipoteza ca masuratorile efectuate pe indivizii din lot sunt independente, adica nu depind unele de altele ceea ce de fapt se si întâmpla în majoritatea cazurilor când este vorba de esantioane de pacienti.

Astfel, testul Student pentru loturi mici poate fi aplicat daca sunt îndeplinite urmatoarele conditii, numite conditii de aplicare pentru teste parametrice:

• Repartitiile populatiilor din care provin loturile sunt normale
• Deviatia standard este aceeasi la cele doua populatii.
• Masuratorile sunt independente.

Exemplu de calcul:

Masurând frecventa cardiaca la 9 pacienti cu hipertiroidie si la alti 9 pacienti cu hipotiroidie, au fost obtinute valorile din tabelul 8.1. Primul pas este calculul mediilor, al deviatiilor standard si al dispersiilor. Cum statistica testului foloseste direct dispersiile, deviatiile standard nu sunt absolut necesare.

Tabelul 8.1 Valorile frecventei cardiace la 9 pacienti cu hipotiroidie si 9 pacienti cu hipertiroidie. Mediile, deviatiile standard si dispersiile sunt calculate

pe ultimele trei linii

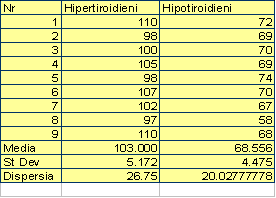
Calculele, decurg în felul urmator:

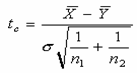
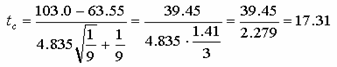
Valoarea prag a lui t_95% din tabele statistice este 2,12. Cum statistica testului depaseste valoarea prag, ipoteza de nul se respinge, diferenta între cele doua medii de esantionare este semnificativa la pragul de semnificatie de 95%.