ORGANIZAREA CA SPATII EUCLIDIENE, NORMATE, METRICE

ORGANIZAREA CA SPAŢII EUCLIDIENE, NORMATE, METRICE

Fie X spatiu vectorial real

Definitie   Functia <,> : X∙X→R se numeste produs scalar pe multimea X daca:

<x,y>=<y,x> ,(simetrie)

(aditivitate īn prima variabila)

(omogenitate īn prima variabila)

Observatie: Produsul scalar <,> este liniar si īn a II-a variabila si este o functionala biliniara ,pozitiv definita.

Exemple:

X=C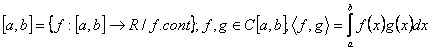

Definitie Se numeste spatiu euclidian un spatiu pe care s-a definit un produs scalar.

Propozitie (Inegalitatea Cauchy Buniakovski)

Intr-un spatiu euclidian X ,are loc relatia:

Exemple:

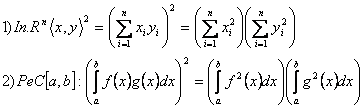
Definitie   Functia:

se numeste norma a spatiului euclidian.

Norma are urmatoarele proprietati:

N1)

N2)

N3) ( inegalitatea triunghiului)

Observatii: 1) se numeste norma indusa de produsul scalar.

2) Din inegalitatea Cauchy Buniakovski se poate defini unghiul dintre x si y.

,

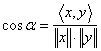Definitie Vectorii x si y se numesc ortogonali daca:

Propozitie Un sistem de vectori nenuli si ortogonali doi cate doi este liniar independent

Definitie O baza a spatiului X se numeste ortogonala vectorii ei sunt ortogonali doi cate doi.

Propozitie Īntr-un spatiu finit dimensional X exista o baza ortogonala.

Procedeul Gramm Schimdt de ortogonalizare a unei baze oarecare,

si determinam astfel īncāt

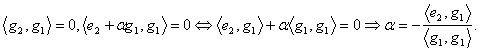
Presupunem ca s-au construit astfel vectorii g₁,g₂,.g_k-1 nenuli si ortogonali doi cāte doi.

Construim determinānd astfel īncāt

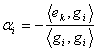sau si

Se obtine baza G=cu vectorii ortogonali doi cāte doi.

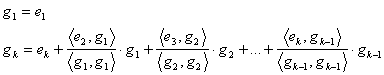
Definitie Functia 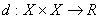se numeste distanta īn X.

Un spatiu vectorial pe care s-a desfinit o distanta se numeste spatiu metric.

Functia distanta are propretatile:

P1)

P2)

P3)

Exemplu: Īn Rⁿ distanta īntre vectorii x,y este

iar norm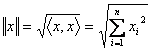a Pt.n=2,n=3 se obtine distanta obisnuita din geometria euclidiana.