VARIABILE ALEATOARE

3.1 Definitia variabilei aleatoare

Majoritatea experimentelor de interes practic au ca rezultate valori numerice. Aceasta īnseamna ca rezultatul unei probe al unui experiment, poate fi caracterizat de un numar sau de un cuplu de numere. Se poate, astfel considera ca fiecarei probe al unui experiment i se poate asocia un numar sau de un cuplu de numere. Se poate atunci introduce notiunea de variabila aleatoare (īntāmplatoare) ca o functie reala definita pe multimea evenimentelor elementare asociate experimentului considerat. Cuvāntul aleator, subliniaza faptul ca se lucreaza cu elemente generate de fenomene īntāmplatoare, care nu sunt guvernate de legi strict deterministe. Elementul dificil īn analiza acestor fenomene consta īn faptul ca desi acestea au o anumita regularitate, este imposibil de precizat cu certitudine rezultatul unei probe īntāmplatoare.

Fie multimea evenimentelor elementare asociata unui anumit experiment, rezultatele posibile fiind notate cu . Este posibil ca acesta sa nu fie un rezultat numeric īn sine, dar i se poate atribui o anumita valoare numerica. De exemplu, la distribuirea unor carti de joc, se poate atribui o anumita valoare numerica fiecarei carti samd.

DEFINIŢIE Orice functie f definita pe si care ia valori īn multimea numerelor reale R, se numeste variabila aleatoare.

Prin urmare, fiecarui rezultat , , īi corespunde numarul real , .

OBSERVAŢIE Numarul rezultatelor , distincte este mai mic cel mult egal cu n.

EXEMPLU Se considera experimentul aruncarii unui zar. Fie , evenimentele care constau īn aparitia fetei cu un numar i de puncte. Se poate defini o variabila aleatoare, ca fiind data de

Se considera acum ca variabila aleatoare f īnregistreaza s valori distincte , īn conditiile īn care sunt īnregistrate n evenimente elementare Fie , evenimentele elementare pentru care , . Notānd , atunci:

.

EXEMPLU Se considera o variabila aleatoare g, data de recolta de grāu pe un hectar. Īn aceasta situatie variabila aleatoare poate avea orice valoare dintr-un interval si prin urmare apare urmatoarea clasificare, generata de natura valorilor īnregistrate.

DEFINIŢIE O variabila aleatoare se numeste discreta (discontinua) daca poate lua numai valori izolate. Numarul valorilor posibile ale unei variabile aleatoare discrete poate fi finit sau infinit.

O variabila aleatoare se numeste continua daca poate lua valori care umplu un interval finit sau infinit. Evident, numarul valorilor posibile ale unei variabile aleatoare continue este īntotdeauna infinit.

3.2 Repartitia unei variabilei aleatoare discrete

Pentru a defini o variabila aleatoare discreta este suficient sa se enumere toate valorile posibile pe care aceasta le poate lua. Īnsa, pentru a o cunoaste complet trebuie enumerate si probabilitatile corespunzatoare fiecarei valori īnregistrate.

Se numeste repartitie a unei variabile aleatoare discrete enumerarea valorilor posibile ale variabilei aleatoare si a probabilitatilor corespunzatoare acestora. De obicei repartitia unei variabile aleatoare discrete se scrie sub forma unui tablou īn care prima linie contine toate valorile posibile, iar a doua linie, probabilitatile corespunzatoare :

, sau

Ţinānd seama ca īntr-un experiment variabila aleatoare ia una si numai una din valorile sale posibile, rezulta ca evenimentele care constau īn aceea ca variabila ia valorile sau ,., sau formeaza - dupa cum se stie - un sistem complet de evenimente. Prin urmare, suma probabilitatilor acestor evenimente este egala cu unitatea :

.

3.3 Operatii cu variabile aleatoare discrete

DEFINIŢIE Puterea de ordinul k a variabilei aleatoare f este variabila aleatoare cu repartitia :

.

DEFINIŢIE Daca este un numar real, produsul dintre si este variabila aleatoare , cu repartitia :

.

Fie si doua variabile aleatoare, avānd respectiv repartitiile:

si .

Se considera evenimentul care consta īn aceea ca ia valoarea , si ia valoarea , . Acest eveniment notat si care este intersectia evenimentelor si , constānd īn aceea ca ia valoarea , respectiv ia valoarea , are o probabilitate bine determinata:

Cum evenimentele , īn numar de , formeaza un sistem complet de evenimente, atunci :

DEFINIŢIE Variabila aleatoare are repartitia:

DEFINIŢIE Variabila aleatoare are repartitia:

,

Exista vreo legatura īntre probabilitatile si ? Raspunsul la aceasta īntrebare este afirmativ, īnsa legatura dintre aceste probabilitati nu este īntotdeauna simpla. Un caz īn care aceasta legatura este foarte simpla este acela īn care si sunt independente.

DEFINIŢIE Variabilele si se numesc independente probabilistic daca pentru orice si , , evenimentele si sunt independente. Prin urmare:

,

adica

.

Īn mod analog se pot defini sumele si produsele a mai mult de doua variabile aleatoare, ca si notiunea de independenta a unui numar oarecare de variabile aleatoare.

3.4 Momentele unei variabile aleatoare discrete

Se considera doua variabile aleatoare si si se presupune ca poate lua valorile , iar poate lua valorile Pentru fiecare pereche , fie probabilitatea ca sa ia valoarea si sa ia valoarea , adica:

DEFINIŢIE Probabilitatile constituie repartitia comuna a variabilelor aleatoare , .

DEFINIŢIE Variabilele aleatoare si sunt independente, daca pentru orice , si orice are loc:

.

Se considera acum mai mult de doua variabile aleatoare. Fie , variabile aleatoare, unde variabila aleatoare ia valorile , .

DEFINIŢIE Probabilitatile :

constituie repartitia comuna a variabilelor aleatoare

DEFINIŢIE Variabilele aleatoare sunt independente, daca pentru orice

DEFINIŢIE Variabilele aleatoare [1] sunt independente, daca orice numar finit de variabile aleatoare din acest sir sunt independente.

Introducem acum o caracteristica numerica foarte importanta, asociata unei variabile aleatoare.

DEFINIŢIE Numarul

se numeste valoarea medie a variabilei aleatoare

EXEMPLU Īn experimentul cu zarul :

DEFINIŢIE Fie un numar īntreg, . Numarul

se numeste moment de ordinul al variabilei aleatoare

OBSERVAŢIE Momentul de ordinul este valoarea medie.

DEFINIŢIE Numarul

se numeste dispersia variabilei aleatoare

Cu ajutorul acestor notiuni introduse, se pot demonstra o serie de proprietati.

PROPRIETATEA 1 Fie o variabila aleatoare si un numar īntreg, . Atunci

Demonstratie Fie variabila aleatoare cu repartitia

Atunci variabila aleatoare va avea evident repartitia :

cu alte cuvinte, valorile si au aceeasi probabilitate ,

si deci

()

Din proprietatea anterioara se deduce imediat:

PROPRIETATEA 2 Fie o variabila aleatoare care poate lua o singura valoare cu probabilitatea (adica). Atunci:

.

PROPRIETATEA 3 Fie o variabila aleatoare si un numar real. Atunci:

.

Demonstratie. Fie variabila aleatoare cu valorile , avānd probabilitatile si fie . Aceasta noua variabila aleatoare ia valorile cu aceleasi probabilitati si deci:

()

PROPRIETATEA 4 Fie variabile aleatoare . Atunci valoarea medie a sumei acestor variabile aleatoare este egala cu suma valorilor medii, adica:

.

Demonstratie. Fie mai īntāi numai doua variabile aleatoare si . Se presupune ca variabila aleatoare ia valorile cu probabilitatile , iar variabila aleatoare ia valorile cu probabilitatile . De asemenea fie :

, , .

Fie  ; aceasta noua variabila aleatoare ia valoarea cu probabilitatea , , . Prin urmare :

Suma , este suma probabilitatilor tuturor evenimentelor de forma , unde indicele este acelasi pentru toti termenii sumei, iar indicele variaza de la un termen la altul, parcurgānd toate valorile de la la . Deoarece evenimentele pentru indici diferiti sunt incompatibile doua cāte doua, suma este probabilitatea producerii unui eveniment oarecare din cele evenimente , . Dar, a spune ca s-a produs un eveniment oarecare din evenimentele , , este echivalent cu a spune ca s-a produs evenimentul . Īntr-adevar, daca s-a produs unul din evenimentele , , este evident ca s-a produs si evenimentul ; reciproc, daca s-a produs evenimentul , atunci īntrucāt variabila aleatoare ia neaparat una din valorile sale posibile , trebuie sa se produca si un eveniment oarecare din evenimentele , . Asadar, fiind probabilitatea producerii unui eveniment oarecare din evenimentele , , este egala cu probabilitatea evenimentului , adica

, .

Īn mod analog se deduce:

, .

Ţinānd seama de aceste expresii īn relatia , se obtine :

Pentru mai mult de doua variabile aleatoare, se procedeaza prin inductie. Fie

si se presupune teorema adevarata pentru . Atunci :

Aplicānd proprietatea pentru doua variabile aleatoare, se obtine :

PROPRIETATEA 5 Dispersia unei variabile aleatoare este data de relatia :

.

Demonstratie.

,

daca se tine seama de proprietatea precedenta. Mai departe, aplicānd de doua ori proprietatea 1., se obtine :

.

PROPRIETATEA 6 Fie si doua variabile aleatoare independente. Atunci valoarea medie a produsului acestor variabile aleatoare este egala cu produsul valorilor medii, adica :

Demonstratie. Se presupune ca variabila aleatoare ia valorile cu probabilitatile , iar variabila aleatoare ia valorile cu probabilitatile . De asemenea :

, ,

si cum f si g sunt variabile independente:

Fie ; aceasta noua variabila aleatoare ia valoarea cu probabilitatea . Prin urmare:

PROPRIETATEA 7 Fie variabile aleatoare independente doua cāte cāte doua. Atunci dispersia sumei acestor variabile aleatoare este egala cu suma dispersiilor, adica:

Demonstratie. Din proprietatea 6 se deduce

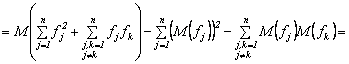
Daca se tine seama de faptul ca variabilele aleatoare sunt independente, atunci din proprietatea 6 rezulta ca cele doua sume duble de mai sus se reduc si deci :

.

PROPRIETATEA 8 (Inegalitatea lui Cebīsev) Fie o variabila aleatoare si un numar pozitiv oarecare. Atunci

,

sau

Demonstratie Fie o variabila aleatoare care ia valorile cu probabilitatile . Dispersia variabilei aleatoare este :

Fie este un numar oarecare; daca din suma de mai sus se elimina toti termenii pentru care si ramān numai termenii pentru care , suma poate numai sa se micsoreze, adica

.

Aceasta suma se va micsora si mai mult daca īn fiecare termen al ei vom īnlocui factorul prin valoarea inferioara:

Suma din partea dreapta reprezinta suma probabilitatilor tuturor acelor valori ale variabilei aleatoare care se abat de la valoarea medie de o parte si de alta cu mai mult de ; conform proprietatii de aditivitate a doua evenimente incompatibile, aceasta este probabilitatea ca variabila aleatoare sa ia una din aceste valori. Cu alte cuvinte, aceasta suma este . Adica :

ceea ce permite aprecierea probabilitatii abaterilor mai mari decāt un numar dat dinainte, cu conditia numai sa fie cunoscuta dispersia .

Cu ajutorul proprietatilor 7 si 8 se poate demonstram urmatorul rezultat foarte important, cunoscut sub numele de legea numerelor mari.

PROPRIETATEA 9 Fie un sir de variabile aleatoare independente care au aceeasi repartitie si deci, aceeasi valoare medie si aceeasi dispersie . Atunci, pentru orice si arbitrari, , exista un numar natural astfel īncāt īndata ce , are loc :

Demonstratie. Din proprietatile 1 si 4, se deduce:

si deci, aplicānd proprietatea 8, se obtine:

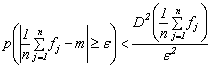
Dar:

,

de unde rezulta:

.

Fiind dati , se poate determina un numar natural , care depinde de si , astfel īncāt īndata ce , sa rezulte :

Prin urmare :

Cu alte cuvinte, proprietatea 9 arata ca daca variabilele aleatoare sunt independente si daca au aceeasi medie si aceeasi dispersie , atunci pentru un suficient de mare, expresia va diferi oricāt de putin de cu o probabilitate oricāt de apropiata de .

Studiul independentei a doua variabile aleatoare se poate realiza si prin intermediul coeficientului de corelatie.

DEFINIŢIE Se numeste corelatie a doua variabile aleatoare, media produsului abaterilor acestora:

.

PROPRIETATE

Demonstratie

DEFINIŢIE Se numeste coeficient de corelatie:

.

TEOREMĂ Corelatia a doua variabile aleatoare independente este nula.

Demonstratie Daca variabilele X, Y sunt independente, atunci si , respectiv sunt independente.

PROPRIETĂŢI

1)  ;

2) daca si numai daca īntre variabilele X si Y exista o relatie de legatura liniara.

Demonstratie 1) Fie 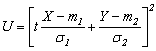, . , . Calculānd media variabilei aleatoare U, se obtine :

.

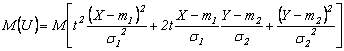
Calculānd discriminantul si impunānd conditia ca acesta sa fie pozitiv, rezulta proprietatea data.

2) Fie , , .

3.5 Repartitii discrete clasice

Repartitia binomiala

Parametrii acesteia sunt : ,

Repartitia Poisson

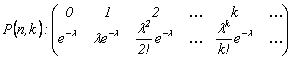
Parametrii acesteia sunt : , .

Repartitia Poisson poate fi scrisa si īn forma:

, .

Distributia hipergeometrica

.

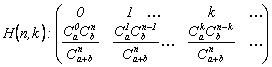Parametrii acesteia sunt : ,

Revenind la calculul parametrilor repartitiilor, se obtine :

Repartitia binomiala

Fie binomul :

.

Derivānd dupa x, rezulta:

Īnmultind cu x, rezulta:

Pentru

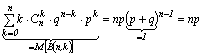
Daca derivam īnca o data dupa x, rezulta:

si īnmultind cu x .

Pentru , de unde rezulta ca:

Repartitia Poisson

Considerānd dezvoltarea īn serie Taylor a functiei īn jurul originii rezulta:

,

.

Atunci

, adica.

Pentru determinarea dispersiei este necesar sa se calculeze:

.

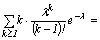
Prin urmare, repartitia Poisson are .

Repartitia hipergeometrica

.

.

.

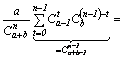
, unde , .

3.6 Mediana, cuantile, moda, asimetrie si exces

DEFINIŢIE Fie o variabila aleatoare care are densitatea de repartitie Se numeste moda a lui si se noteaza cu abscisa punctului de maxim a lui

Daca are un singur maxim, atunci se numeste unimodala, iar daca are mai multe puncte de maxim se va numi plurimodala.

EXEMPLU Se poate observa usor ca daca , atunci are un singur maxim īn si deci

OBSERVAŢIE Īntre valoarea medie , mediana si moda exista asa numita relatie a lui Pearson:

DEFINIŢIE Raportul

daca exista, se numeste asimetrie a repartitiei lui , sau a lui

DEFINIŢIE Expresia

daca exista se numeste exces.

OBSERVAŢIE Marimile sau indicatorii numerici definiti mai sus sunt utili īn general īn statistica pentru a studia diferite repartitii.

3.7 Functia de repartitie

DEFINIŢIE Pentru orice variabila aleatoare , de numeste functie de repartitie a lui functia

.

OBSERVAŢIE Din definitie, se observa, ca daca este o variabila aleatoare discreta, atunci este data de suma tuturor probabilitatilor valorilor lui situate la stānga lui .

EXEMPLU Fie . Atunci, conform definitiei :

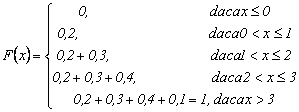
Expresia se numeste salt al functiei īn punctul si se poate observa ca:

.

PROPOZIŢIE Daca este o variabila aleatoare discreta si functia de repartitie a acesteia, atunci pentru orice doua numere date, Are loc:

Demonstratie. Fie , , si . , , . Ca urmare a proprietatilor probabilitatii , se poate scrie ca:

,

,

adica tocmai afirmatiile din propozitie.

PROPOZIŢIE Daca este functia de repartitie a variabilei aleatoare , atunci , ( este nedescrescatoare).

Demonstratie. Din propozitia 1.:

, adica

3.8 Functia generatoare de momente

DEFINIŢIE Daca exista, expresia

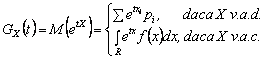
se numeste generatoare de momente asociata variabilei aleatoare .

OBSERVAŢIE Precizarea ,,daca exista'' se refera la convergenta sumei sau a integralei cānd acestea o cer. Se presupune ca si derivatele sale de ordin superior exista. Īn plus, se constata ca:

OBSERVAŢIE Utilizarea functiei generatoare de momente este recomandata atunci cānd se pot calcula mai repede momentele decāt pe cale directa.

EXEMPLU Fie , , , , .

Atunci .

3.9 Functia caracteristica

DEFINIŢIE Fiind date variabilele aleatoare si , se numeste variabil& 919b12j #259; aleatoare complexa , unde se numeste partea reala, iar se numeste partea imaginara. Valoarea medie a lui este, prin definitie .

Fie o variabila aleatoare reala cu functie de repartutie este o variabila aleatoare complexa, avānd si deci, marginita. Valoarea medie a acesteia exista si este o functie , , pe care o numim functie caracteristica a variabilei aleatoare .

DEFINIŢIE Numim functie caracteristica a variabilei aleatoare expresia:

presupunānd ca suma este convergenta.

PROPOZIŢIA 1

PROPOZIŢIA 2 Doua functii de repartitie si sunt identice daca si numai daca functiile lor caracteristice si coincid.

PROPOZIŢIA 3 Fie si doua variabile aleatoare. Daca , atunci

Demonstratie

.

PROPOZIŢIA 4 Daca si sunt variabile aleatoare independente, atunci

Demonstratie

PROPOZIŢIA 5 Daca momentul de ordinul () al unei variabile aleatoare exista, atunci derivata exista pentru orice si au loc relatiile :

EXEMPLUL 1

3.10 Probleme rezolvate

1. Variabila aleatoare are si . Se cere o margine inferioara pentru probabilitatea

Solutie. Inegalitatea lui Cebīsev : ,

. , deci

, de unde, conform inegalitatii lui Cebīsev: .

2. Pentru variabila aleatoare sunt cunoscute media si momentul initial de ordinul doi . Stabiliti o margine inferioara pentru probabilitatea .

Solutie. Putem determina dispersia variabilei . Din

.

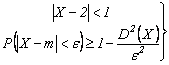
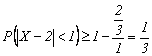3. Sa se determine dispersia variabilei aleatoare cu media si daca inegalitatea lui Cebāsev este

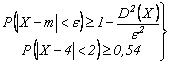
Solutie. si , , .

. Variabila aleatoare discreta este data de 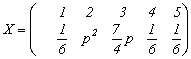. Determinati constanta si aflati .

Solutie. este variabila aleatoare daca astfel īncāt

, .

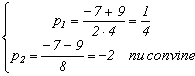Distributia variabilei este .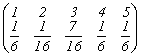

.

5. Consideram ca si sunt variabile aleatoare independente, iar distributiile lor sunt:

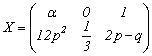
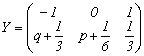
Sa se scrie distributia variabilelor , , , . Pentru ce valori ale lui  ?

Solutie.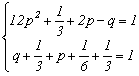

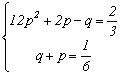
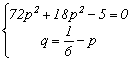
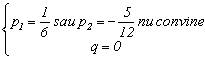
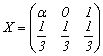
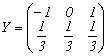
Distributia variabilei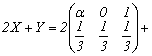

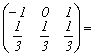
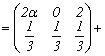
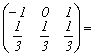
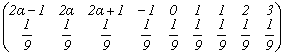
3.11 Probleme propuse

1. Fie X si Y doua variabile aleatoare discrete ale caror repartitii sunt date īn tabelele incomplete de mai jos:

a) Sa se completeze tabelul īn fiecare caz (daca este posibil) pentru ca sa contina repartitia comuna () precum si repartitiile individuale () si () ale lui si ;

b) scrieti variabilele aleatoare si corespunzatoare;

c) calculati .

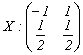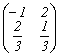2. Fie variabilele aleatoare si . Daca sa se determine repartitia comuna a variabilelor aleatoare si si apoi sa se calculeze .

3. Pentru variabilele aleatoare:

a) 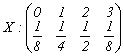; b) ;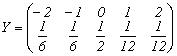

a₁) calculati , , , , , ;

a₂) care din urmatoarele marimi pot fi calculate si care nu? De ce?

a₃) calculati marimile de la punctul a₂) pentru care raspunsul este afirmativ.

4. Fie variabila aleatoare discreta 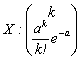. Sa se calculeze functia generatoare si apoi functia caracteristica si cu ajutorul acestora, pe rānd sa se determine si .

5. Calculati functia generatoare de momente si functia caracteristica pentru variabilele aleatoare

1) 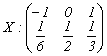; 2)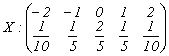

si apoi verificati daca momentele obtinute pe cale directa coincid cu cele obtinute cu ajutorul acestor functii.

6. Scrieti functia de repartitie si schitati graficul acesteia pentru variabilele aleartoare:

; .

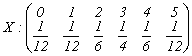7. Fie variabilele aleatoare independente:

; .

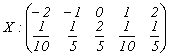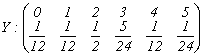a) calculati , , , , , ;

b) care din urmatoarele marimi pot fi calculate si care nu? De ce?

c) calculati marimile de la punctul b) pentru care raspunsul este afirmativ.

8. Fie variabilele aleatoare 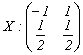si . Daca , sa se determine repartitia comuna a variabilelor aleatoare si si apoi sa se calculeze . Sa se faca discutie dupa .

9. Daca , , , si . Calculati pentru:

.

10. Sa se determine variabilele aleatoare si , stiind ca, , si . Calculati apoi , si presupunānd ca X si sunt independente.

11. Fie variabilele aleatoare

1) 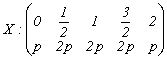; 2) .

a) sa se determine variabilele aleatoare;

b) sa se scrie functia de repartitie;

c) Sa se reprezinte grafic

12. Fie variabilele aleatoare 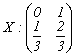si 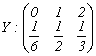. Daca si determinati repartitia comuna a variabilelor aleatoare si si apoi calculati .

13. Fie variabila aleatoare discreta , , . Sa se calculeze functia generatoare si apoi functia caracteristica si cu ajutorul acestora, pe rānd sa se determine si .

14. Sa se determine variabilele aleatoare:

si stiind ca si . Sa se calculeze apoi ; , , si .

15. Daca si sunt doua variabile aleatoare astfel ca,, si , sa se calculeze pentru stiind ca .