Cānd reducerea se face la axul unui mecanism al ML <
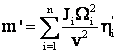 .
.
La stabilirea masei totale redusa la un ax oarecare
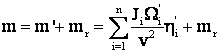 .
.
CONSIDERAŢII PRIVIND CULUL
M.E.A.
Discutie ec. E. M.
![]()
cuplul static rezistent
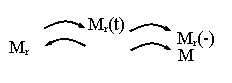
cupluri statice potentiale acelea cu semn (+) sau (-)
cupluri statice de reactie sau cupluri statice reactive tot tipul (+)
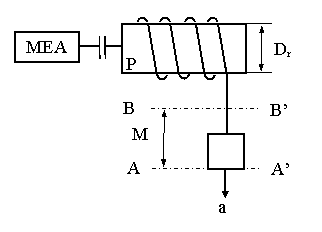 La pornirea MEA pt. ridicarea
sarcinii
La pornirea MEA pt. ridicarea
sarcinii
![]() - īn cazul
cuplarii directe
- īn cazul
cuplarii directe
![]() , iar
, iar ![]()
![]()
La ridicarea sarcinii īn regim stabilizat
(v
= ct. sau W
= ct.)
![]()
deci Md M =Mr
La frānarea motorului īn timpul ridicarii sarcinii
![]()
Īntrucāt Mr > Md (de obicei) M > 0.
La pornirea motorului pt. coborārea sarcinii
cuplul dat de sarcini īn
coborāre este de acelasi sens cu cuplul motorului
Mr <
0, iar W Md
> 0
M = -Mr + Md
daca ![]() va lucra īn regim de
frānare
va lucra īn regim de
frānare
daca ![]() nu dezvolta cuplu
trebuie frāna mecanica
nu dezvolta cuplu
trebuie frāna mecanica
daca ![]() dezvolta cuplu de
accelerare.
dezvolta cuplu de
accelerare.
Asupra
cuplului static
![]()
f - cuplu de frecari
n - cuplu static util
Mf > 0 totdeauna (reactiv)
Mn īnsa (potential)
Daca
![]() - sarcina de
coborāre mica
- sarcina de
coborāre mica
- sau mecanismul de ridicare a sarcinii coboara gol
Daca ![]() , deci la pornire
, deci la pornire
M = Md pt. imprimarea acceleratiei.
Daca
![]() , deci semnul lui M este dat de valoarea absoluta a
cuplului static si cel dinamic.
, deci semnul lui M este dat de valoarea absoluta a
cuplului static si cel dinamic.
La coborārea sarcinii īn regim stabilizat
Deoarece
![]() .
.
Semnul cuplului static depinde de raportul dintre cuplul static de frecare si valoarea absoluta a cuplului static util.
La frānarea motorului īn timpul coborārii sarcinii
Mr
0, iar ![]() , din cauza lui
, din cauza lui ![]() M = Mr - Md
M = Mr - Md
Deci
semnul lui M este precizat īn primul rānd de semnul lui Mr, īn functie de
raportul dintre cuplul static la frecari Mf si valoarea absoluta
a cuplului static util ![]() .
.
Daca Mr < 0 Md < 0 - MEA va functiona īn regim de frāna.
Daca
Mr > 0
semnul
lui M este dat de raportul Mr
si ![]() .
.
Graficul de sarcina pt. "tc" ca semn si valoare pt. fiecare perioada.
STABILIREA GRAFICULUI DE VARIAŢIE A LUI "M" IAR "tc" COMPLET DE FUNCŢIONARE A S.A.E.
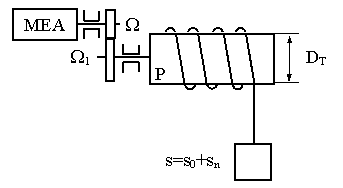 Īntre
M si Toba un organ de transmisie cu i si h
Īntre
M si Toba un organ de transmisie cu i si h
Pt. perioada de pornire la ridicarea sarcinii maxime:
s = s + sn
s - greutatea cārligului
sn - sarcina utila ridicata
M - cuplul pe arborele motor la ridicarea sarcinii maxime
M - cuplul pe arborele motor la coborārea sarcinii maxime
Deci: La pornire:
![]()
![]() si
si ![]() si deci:
si deci:
![]()
asadar: ![]() , deci:
, deci: 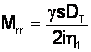 .
.
Sarcina se deplaseaza liniar cu "a"
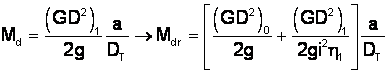
![]() - momentul de volant
al pieselor īn miscare de rotatie de pe arborele motorului
- momentul de volant
al pieselor īn miscare de rotatie de pe arborele motorului
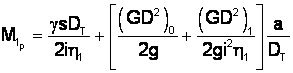 .
.
pt. perioada de regim stabilizat la ridicarea sarcinii maxime
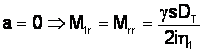
pt. perioada de frānare la ridicarea sarcinii maxime
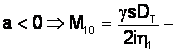
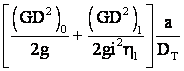
OBS
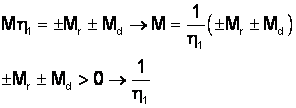
daca
![]() .
.
pt. perioada de pornire la coborārea sarcinii maxime:
![]() , iar
, iar ![]() si este > 0
si este > 0
deci ca semnul cuplului rezistent static total este:
![]()
este dat de valoarea lui g, anume
pt. g <2, ![]()
pt. g = 2, ![]()
pt. g > 2, ![]()
|
M |
|
Mr |
Pentru a se putea determina sensul de transmitere al energiei, sa se stie si Md, iar ac. este > 0.
Deci Mrt
daca ![]() miscarea se
produce de la ML la MEA
miscarea se
produce de la ML la MEA
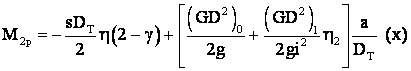
daca ![]() deci cuplul dinamic
necesar pt. accelerare la coborārea sarcinii maxime va fi furnizat de
īnsasi sarcina īn coborāre (fara interventii a MEA)
deci cuplul dinamic
necesar pt. accelerare la coborārea sarcinii maxime va fi furnizat de
īnsasi sarcina īn coborāre (fara interventii a MEA)
daca ![]()
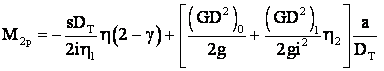
Dat fiind īnsa ca este
vorba de pornire la coborārea sarcinii maxime 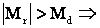 ac. relatie (x)
ac. relatie (x)
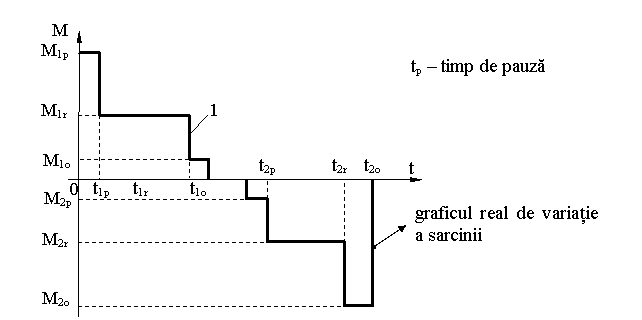
pentru perioada de regim stabilizat la coborārea sarcinii maxime
![]()
pentru perioada de frānare la coborārea sarcinii maxime pt. ca a < 0
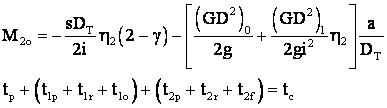
sarcina la cārlig poate varia īnsa īntre s .....(s +sn
graficul de sarcina pt. deplasare īn gol s
se va considera un grafic de sarcina mediu din 1 si 2
calcule eficiente si apropiate de realitate
pt. ML cu Mr reactive trasarea graficelor de sarcina se simplifica Mr ~ Md la oprire (metode de frānare)
METODĂ GRAFICĂ PENTRU DETERMINAREA VALORII sI SEMNULUI CUPLULUI REZISTENT TOTAL PE ARBORELE MOTORULUI
![]() 1
- pornire ridicare
1
- pornire ridicare
2 - regim stabilizat la ridicare
3 - oprire la ridicare
4 - pornire la coborāre
5 - regim stabilizat la coborāre
6 - oprire la coborāre
Constructia
grafica este facuta īn ipoteza ca randamentul trans. ![]() .
.
Īn sistemul s0M:
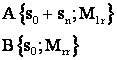
s - cārlig
sn - sarcina utila (sarcina maxima)
M1r - cuplul rezistent static raportat īn regim stabilizat la ridicare
![]() sarcina maxima
sarcina maxima
M3r - cuplul rezistent static raportat la ridicarea īn gol (s
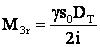
Dreapta
![]() permite sa se
determine Mrr,
la ridicare, pt. "
sarcina īntre s
si s +sn si chiar mai mare.
permite sa se
determine Mrr,
la ridicare, pt. "
sarcina īntre s
si s +sn si chiar mai mare.
Cuplul dinamic raportat
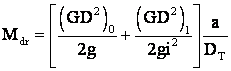
Īn
ipoteza ca Md
si a = ct., indiferent de sarcina segmentele: ![]()
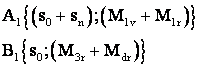 dreapta
dreapta ![]() permite sa se
determine cuplul Mr
total pt. perioada pornirii la ridicarea oricarei sarcini.
permite sa se
determine cuplul Mr
total pt. perioada pornirii la ridicarea oricarei sarcini.
Īn mod analog:
![]() si
si 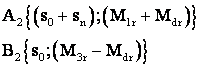 din
din ![]() permite determinarea Mrr la oprire a ridicare.
permite determinarea Mrr la oprire a ridicare.
Īn
punctul ![]() unde
unde
![]() - Mr la coborārea sarcinii
maxime īn regim stabilizat.
- Mr la coborārea sarcinii
maxime īn regim stabilizat.
Deci
![]() - permite det. Mrr pt. orice sarcina
la coborāre.
- permite det. Mrr pt. orice sarcina
la coborāre.
Daca se ia la fel ca si pentru ridicare
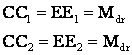
![]() care permite det. Mrr pt. pornire la coborāre
care permite det. Mrr pt. pornire la coborāre
![]() oprire la coborāre
oprire la coborāre
![]() cu verticala de
abcisa s E a
carei ordonate
Mrr la
coborāre īn gol (s
cu verticala de
abcisa s E a
carei ordonate
Mrr la
coborāre īn gol (s
constructia grafica pt. ML a carei Mr este de tip potent.
pt. tip reactiv se rezuma
doar la ![]() .
.
DETERMINAREA MOMENTELOR DE INERŢIE (VOLANT) ALE ELEMENTELOR UNUI S.A.E.
J det. M semn, valoare
- īn regim tranzitoriu
- momente de inertie (de volant) interne (J
- momente de inertie (de volant) externe (Je
-
laminoare reversibile 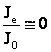
-
la MU ![]()
-
SAE cu volant 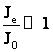 (10)
(10)
Det. lor se poate face: calcul, experimental, dupa cataloage sau empiric.
Determinarea mom. de inertie pe baza de calcul analitic
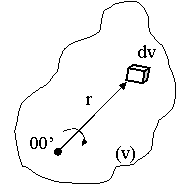
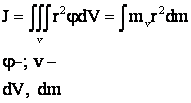
simplificare pentru cazuri particulare cānd axa de rotatie trece prin centrul de greutate al corpului
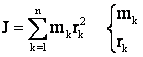 sau pentru calcule
practice
sau pentru calcule
practice ![]()
UM kg m
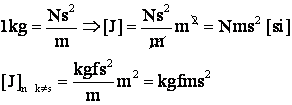
- raza de inertie prin "C"
DETERMINAREA MOMENTELOR DE INERŢIE PRIN METODE EXPERIMENTALE
De ex.:
metoda īncetinirii (sau lansarii)
metoda caderii greutatii
metode de oscilatie
METODA ĪNCETINIRII
atāt intern cāt si total
Det. mom. de volant al rotorului motorului
n Watt-metru P
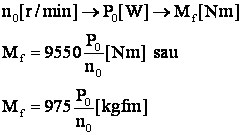
Dni Dti 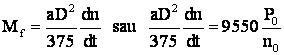
deci
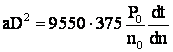 sau
sau 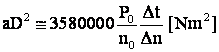 cu
cu ![]()
dar
![]()
cu
![]() la curba n(t) din n
la curba n(t) din n
deci
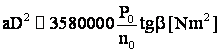 .
.
Determinarea momentului de inertie (de volant) total al sistemului
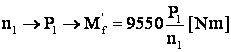
iar la decuplarea mot. 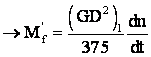
(aD - mom. de volant total (int. plus ext).
METODA CĂDERII GREUTĂŢII
moment de inertie intern (pt. mot. de putere redusa)
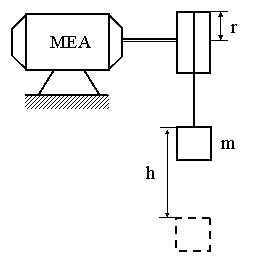 r,
m, h, t
r,
m, h, t
![]()
sau
![]()
Deoarece
![]()
adica
![]()
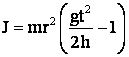
deci din m, r, h, t J.
METODE DE OSCILAŢIE
Pt. rotoare de m.c.a.: - oscilatii de torsiune
- oscilatii pendulare
Metoda bazata pe oscilatii de torsiune
![]()
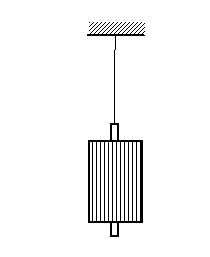 ax. torsiune
ax. torsiune 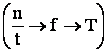
![]()
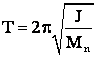 Mn cuplu de torsiune pt. a produce o
Mn cuplu de torsiune pt. a produce o
torsiune de "m" radiani
M a ![]()
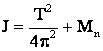 .
.
Dar:
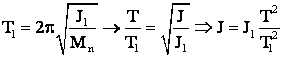
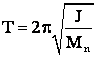
Metoda bazata pe oscilatii pendulare
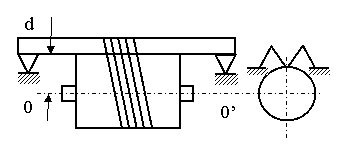
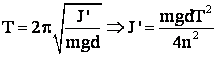
(īn raport cu axa la "d" de 00')
STEINER J īn rap. cu 00'
J'=J=md sau J = J'- md =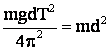
sau:
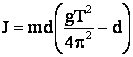
- Metode empirice q.e.d.
C.M. si R.F. ale M.L.
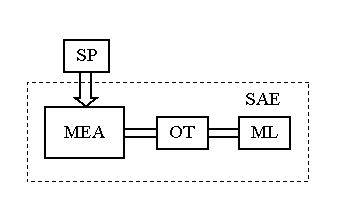 MEA si ML+OT
MEA si ML+OT
C.m. a ML Mr(m+f)
a, x....)
R.F. = f(t) al ML
Mrt = f(t)
- functie de c.m.
- clasificare
- functie de R.F.
CLASIFICAREA M.L. ĪN FUNCŢIE DE C.M.
M.L.
M.L. la care ![]()
M.L. la care ![]()
M.L. la care ![]()
M.L. la care ![]()
![]()
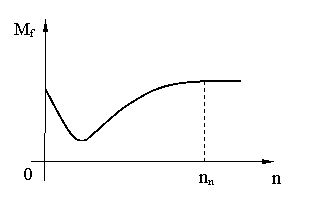
CONSIDERAŢII GENERALE ASUPRA CUPLURILOR REZISTENTE DATORATE FRECĂRILOR
la funct. īn gol Mr ~ Mf
![]()
![]() si lim.
si lim.
pt. un lant cinematic f. complex Mr det. de Mf (ca forma si valoare)
probleme la pornire
probleme la ML la care Mf ~ Mr u
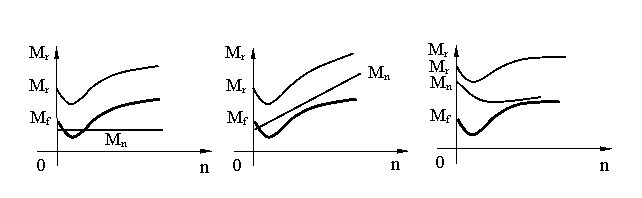
- Mf Mr (la pornire)
Am - c.m. dat de MEA
Ar - c.m. dat de ML
Af - c.m. dat de frecari
M
ML 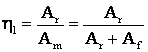 , daca
, daca ![]()
Cānd
ML M ![]()
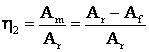 , daca
, daca ![]() .
.
C.M. ALE M.L.
C.M. ale M.L. cu Mr = f(n)
Expr.
gen: ![]()
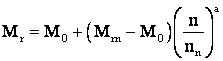
M - cuplul de mers īn gol
Mr - cuplul rezist. static f(n)
Mrn nn cuplul nominal
a = - 1; 0; 1; 2; sau 5; 6 - mici variatii.
-
īn marimi relative 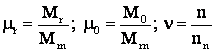
![]()
pt. a = - 1 ![]()
pt. ![]()
asimptote axa ordonatelor si o paralela la abscisa de ordonata m0i
![]() si
si ![]()
la mas. unelte aschietoare
mas. de depanat si oriunde se reclama un asemenea regim de functionare.
pt. a = 0
![]()
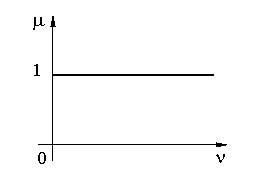
![]()
masimi de ridicat, deplasare poduri, ascensoare, benzi transportoare, laminoare, ascensoare cu funie de echiplibrare, calandre din ind. hārtiei.
pt. a = 1
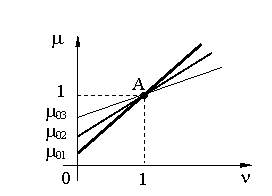
![]()
calandrele din ind. textila
valturile din ind. cauciucului
pt. a = 2 ![]()
pt. diferiti m
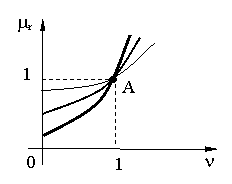
cu cāt ![]() o īnclinare mai mica
o īnclinare mai mica
ventilatoare, pompe centrifuge, elice, propulsoare de pe mare, turbocompresoare
a = 5; 6 - la M.L. de viteza mare si f. mare: supracentrifuge, ultracentrifuge din ind. chimica si alimentara.
C.M. ALE M.L. CU CUPLU REZISTENT STATIC DEPENDENT DE "a ![]()
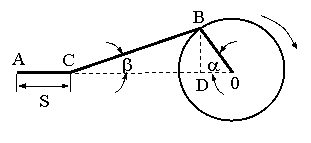 vc = ? - a glisierei C
vc = ? - a glisierei C
Notam cu "s" cursa pe care o executa glisiera C
![]() se observa
ca s = 0A - 0C
se observa
ca s = 0A - 0C
dar 0A = r + b, iar
![]()
Deci: ![]() .
.
Din
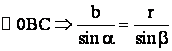 , adica
, adica 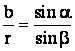 sau
sau
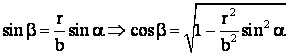 .
.
Din dezvoltarea īn serie 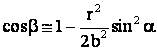
si
deci 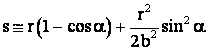 , dar r << b
, dar r << b
si
deci: ![]()
dar
![]()
deci mecanismul functioneaza permanent īn regim tranzitoriu:
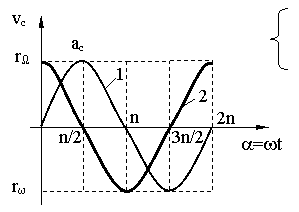 vc(t)
vc(t)
ac(t)
![]()
definesc raportul de transmitere al mecanismului bielei manivelei:
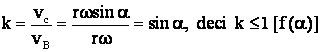
vB = rw - viteza periferica a fusului.
Dinamica sistemelor de actionare a ML cu mec. biela-manivela
Din EFM:
![]() necesitatea determinarii expr. Mrr si a lui Jr, ambele raportate la
arborele MEA.
necesitatea determinarii expr. Mrr si a lui Jr, ambele raportate la
arborele MEA.
- pt. det. cuplului rezistent static se considera fig.
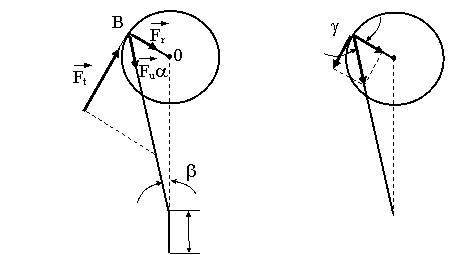
Fu - forta utila ce se transmite prin biela
Ft - forta tg; Fr - forta radiala
Ft - produce cuplu
Dar: ![]()
dar: 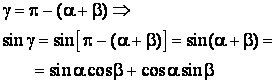
Dar: ![]() si
si 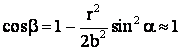
Asadar: ![]() .
.
Prin urmare:
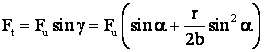 .
.
Cuplul rezistent util pe axul "O" al mec. biela-manivela
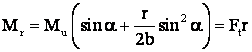 .
.
Daca īntre axul "O" si arborele motorului este un OT, cu "ht" si "i"
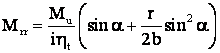 .
.
Dar mom. "J" numar de momente.
J0r - mom. de inertie axial al organelor īn misc. de rotatie (manivela, arborele O, etc)
Jbg - moment de inertie axial al bielei, fata de un ax ce trece prin centrul de greutate "G" al bielei, perpendicular pe axul bielei
Jt - un mom. de inertie fictiv datorat maselor īn miscare de translatie (glisiera ....)
![]()
![]() , deci din
, deci din ![]()
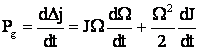 dar
dar
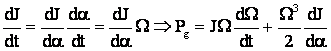
Deci: 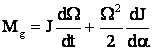 sau
sau ![]()
deci
EFM 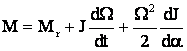 .
.
Aceasta este ec. generalizata a miscarii, cānd J = ct. ec. obt. este EFM cunoscuta deja.
Deci expr. lui J, se pleaca de la expr. energ. cinetice = cu o suma a tuturor pieselor īn rot. sat translatie.
centrul de greutate al bielei misc. de tr. cāt si rotatie īn jurul centrului de greutate (rb si Wb
![]()
mb - mom. bielei
mc - masa glisierei rc
Deci: ![]()
sau 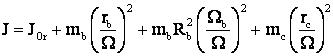 .
.
Rb - raza de inertie a bielei.
Deci trebuiesc cunoscute: vb Wb si rc
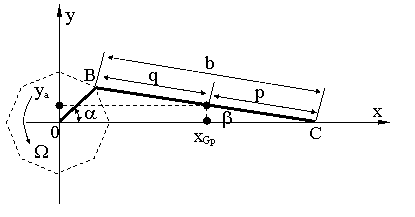 Din
figura
Din
figura
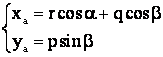
cu expresiile lui sinb si cosb, stabilite anterior.
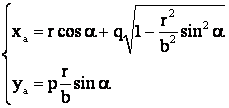
Dar 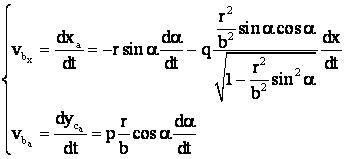
Īntrucāt
![]()
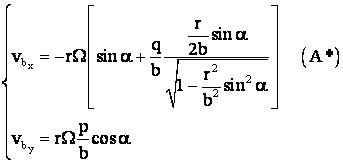
Deci
viteza punctului G
va fi: ![]() .
.
Iar
pt. glisiera, mai exact
din componentele ![]() din relatia (A*) la care se ia q = b
si p = 0
din relatia (A*) la care se ia q = b
si p = 0
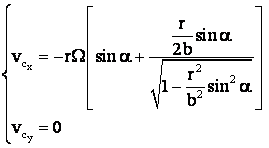
![]()
|