PROIECTAREA UNUI MECANISM CU ROŢI DINŢATE
.1 DETERMINAREA GRADULUI DE MOBILITATE AL
.DETERMINAREA NUMĂRULUI DE DINŢI AL ROŢII 3 , A VITEZELOR UNGHIULARE sI A RAPOARTELOR DE TRANSMITERE
3.3.CALCULUL NUMĂRULUI DE SATELIŢI ns
3.4 DETERMINAREA PARAMETRILOR GEOMETRICI AI ROŢILOR 5 sI 6
3.5 REALIZAREA DESENULUI DE EXECUŢIE
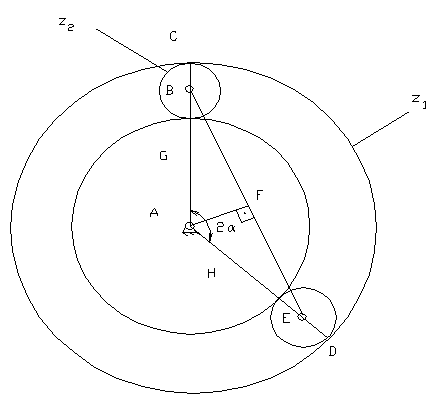
Sa se proiecteze mecanismul cu roti dintate din figura , cunoscând urmatoarele date:
turatia n1=250rot/min
modulul normal mn=2mm
unghiul de înclinare
nr. de dinti al rotii 2 z2=20
nr. de dinti al rotii 3 z3=19
nr. de dinti al rotii 4 z4=45
nr. de dinti al rotii 5 z5=18
nr. de dinti al rotii 6 z6=40
Mecanismul elementar cu roti dintate este format din doua elemente dintate (roti dintate), mobile în jurul a doua axe cu pozitie relativ invariabila, unul antrenându-l pe celalalt prin actiunea dintilor aflati succesiv în contact.
Transmiterea miscarii între doua roti dintate conjugate (care angreneaza una cu alta) se face prin intermediul unei cuple superioare. Suprafetele dintilor care formeaza cupla se numesc flancuri.
CLASIFICAREA ANGRENAJELOR
Unul dintre criteriile de clasificare al angrenajelor este legat de variatia raportului de transmitere. Daca raportul de transmitere este constant, axa instantanee a miscarii relative are o pozitie invariabila, iar suprafetele de rostogolire sunt de revolutie. Rotile dintate care formeaza astfel de mecanisme se numesc circulare. Când raportul de transmitere este variabil suprafetele de rostogolire nu sunt de revolutie, iar rotile se numesc necirculare.
Un criteriu de clasificare important îl constituie pozitia relativa a axelor. În mod firesc, pozitia relativa a axelor determina forma suprafetelor de rostogolire. Conform acestui criteriu se întâlnesc:
angrenaje cu axe paralele si cu suprafete de rostogolire cilindrice;
angrenaje cu axe concurente si cu suprafete de rostogolire conice;
angrenaje cu axe încrucisate si cu suprafete de rostogolire în forma de hiperboloizi de rotatie cu o pânza.
O importanta deosebita, pentru definirea geometrica a rotilor dintate, prezinta cazurile în care dintre suprafetele de rostogolire se reduce la un plan. Daca acest element are miscare de rotatie se numeste roata plana, iar daca are miscare de translatie - cremaliera.
În categoria angrenajelor paralele se întâlneste angrenajul particular format dintr-o roata cu suprafata de rostogolire cilindrica si cu cremaliera. Axa de translatie a cremalierei este perpendiculara pe axa de rotatie a rotii, deci mecanismul sete plan.
Angrenajele concurente înregistreaza cazul particular în care angreneaza o roata cu suprafata de rostogolire conica si o roata plana.
Angrenajul încrucisat prezinta doua situatii particulare: un angrenaj format dintr-o roata cu suprafata de rostogolire cilindrica si o cremaliera, formând un mecanism spatial si un angrenaj format dintr-o roata cu suprafata de rostogolire conica si o roata plana.
Dupa modul de definire, rotile dintate si angrenajele formate cu ajutorul lor se clasifica în felul urmator:
Roti dintate cilindrice - au suprafata de divizare cilindrica. Doua roti cilindrice formeaza un angrenaj cilindric, care poate fi cu axe paralele sau cu axe încrucisate (angrenaj elicoidal).
Roti dintate conice - au suprafata de divizare conica si se definesc printr-un angrenaj fictiv concurent. Doua roti conice cu axe concurente formeaza un angrenaj conic.
Roti dintate pseudoconice - se definesc cu ajutorul unei roti de referinta plane, cu care formeaza un angrenaj fictiv încrucisat. Suprafata de divizare este un con.
Roti dintate hipoide - roti conice sau pseudoconice care formeaza un angrenaj încrucisat, numit angrenaj hipoid.
3.1.DETERMINAREA GRADULUI DE MOBILITATE AL MECANISMULUI
n=5
c5=4(A;D;F;G)
c4=3(B;C;E)
M=3(n-1)-2c5-c4=3(5-1)-2*4-3=1
Deci mecanismul are gradul de mobilitate 1.
De aici rezulta ca avem de-a face cu un mecanism planetar.
3.2.DETERMINAREA NUMĂRULUI DE DINŢI AL ROŢII 1, A VITEZELOR UNGHIULARE sI A RAPOARTELOR DE TRANSMITERE
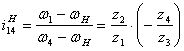
![]()
![]()
![]()
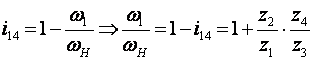
Nu cunoastem numarul de dinti al rotii 1;de aceea ne folosim de conditia de coaxialitate dintre axul rotii 2 si axul rotii 3.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() dinti
dinti
![]()
![]()
![]()
![]()
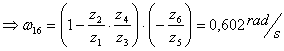
c
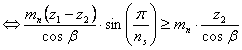
![]()
2.Conditia de montaj:
![]()
![]()
Pentru a calcula numarul de sateliti ,în relatiile
(1),(2),(3) luam pe ns ,
astfel încât k![]() Z.
Z.
ns=1: (64-19)sin /ns >Z 45sin >20; --nu este verificata conditia(1)
ns=2: (Z -Z )sin /ns>Z ; 45sin /2>20 --se verifica conditia (1)
+Z ) sin /ns>Z ; 63sin /2>19 -se verifica conditia (2)
(Z *Z -Z *Z ns=k; 13 este nr. Intreg -se verifica conditia (3)
Rezulta ca numarul de sateliti ns
|
Elementul geometric |
Formula de calcul sau /si indicatia de adoptare |
Valoare numerica |
|
Angrenaj cu dinti înclinati |
||
|
|
|
|
|
Date initiale privind definirea geometrica a danturilor angrenajului |
||
|
Numerele de dinti
|
|
Z5=18 Z6=40 |
|
Unghiul de înclinare a dintelui |
|
|
|
Modulul (standardizat) |
STAS 822-82 |
ms=2 |
|
Modulul normal |
STAS 822-82 |
mn=2 |
|
Profilul de
referinta standardizat |
STAS 821-82 |
αno=20˚ hao=1 co*=0,25 |
|
Parametri de baza ai rotilor de baza si ai angrenajului |
||
|
|
|
αn=200 hao*=1 co*=0,25 |
|
Unghiul de presiune de referinta frontal |
|
αt=20,090 |
|
Modulul frontal |
|
mt=2,04 |
|
Distanta între axe de referinta |
|
a=58 |
|
Distanta între axe aw |
Se rotunjeste la o valoare întreaga sau conform STAS 6055-82 |
aw=62 |
|
Unghiul de angrenare frontal |
|
αtw=29,320 |
|
Coeficientul normal al deplasa- pinionului
rotii 4 |
|
ξa5=0,865 ξa6=0,531 |
|
Alunecarea relativa la piciorul dintelui, pinionului 3 rotii 4 |
|
ξa6=- 6.43 |
|