VARIABILE ALEATOARE. FUNCŢII DE REPARTIŢIE. INDICATORI STATISTICI

realizeaza niciodata în cadrul unui experiment dat.

Evenimentele ce apar ca rezultat al unor experimente le vom nota , etc. Evenimentul complementar unui eveniment este acel eveniment care se realizeaza atunci si numai atunci când nu se realizeaza Evenimentul care consta în realizarea simultana a evenimentelor se noteaza cu (se citeste evenimentul si

Probabilitatea unui eveniment este o masura a sanselor de realizare a acelui eveniment. Daca un eveniment se desfasoara astfel încât producerea oricarui eveniment legat de acesta are un numar finit de sanse egal-posibile, probabilitatea evenimentului este raportul dintre numarul rezultatelor favorabile producerii evenimentului si numarul tuturor rezultatelor posibile.

Se considera exemplul cunoscut al urnei care contine bile de aceeasi marime, dintre care sunt albe si sunt negre. Probabilitatea de a extrage o bila alba sau neagra va fi

, (2.1)

respectiv

. (2.2)

Din relatia (2.1) se vede imediat ca probabilitatea unui eveniment este cu 535h79f prinsa între zero si unitate, adica

Evident, când în urna sunt numai bile negre, iar când în urna sunt numai bile albe etc.

Teorema probabilitatii totale

Sa presupunem ca pentru producerea unui eveniment din cazuri posibile, egal probabile, sunt cazuri favorabile, adica

(2.3)

De asemenea, pentru producerea evenimentului , pentru care avem cazuri favorabile, putem scrie

(2.4)

Se mai considera ca cele doua evenimente se exclud reciproc, adica când se produce , nu se produce

Probabilitatea ca în cele cazuri posibile sa se produca sau , va fi

(2.5)

relatie care reprezinta principiul probabilitatii totale, si anume:

Când un eveniment se poate realiza în mai multe moduri posibile care se exclud reciproc, probabilitatea producerii lui este egala cu suma probabilitatilor care corespund diferitelor moduri de producere.

Teorema probabilitatii compuse

Se considera cazul unui eveniment mai complex care rezulta din realizarea succesiva a doua evenimente dependente si . Pentru examinarea acestei situatii mai presupunem:

- în cazuri se produce atât evenimenul cât si

- în cazuri se produce evenimenul dar nu se produce

- în cazuri se produce evenimenul dar nu se produce

- în cazuri nu se produce nici nici

Fie numarul de cazuri total posibile.

Pentru producerea evenimentelor si probabilitatea este

si (2.6)

Pentru a se produce , probabilitatea este

(2.7)

deoarece are , cazuri favorabile, fiind acelasi.

Dupa ce s-a produs evenimentul , ramâne sa examinam probabilitatea lui . Evident, acesta are numai cazuri favorabile. Deoarece producerea lui este conditionata de aceea a lui (numai acele cazuri vor fi favorabile când are loc ), numarul cazurilor posibile pentru va fi . Prin urmare,

Pentru probabilitatea definita de (2.8), se foloseste notatia ceea ce înseamna probabilitatea ca sa se produca dupa ce s-a produs (probabilitate conditionata).

Din compararea relatiilor (2.6), (2.7) si (2.8) rezulta principiul probabilitatii compuse

si (2.9)

care arata ca: Daca producerea unui eveniment presupune realizarea altor evenimente si , atunci probabilitatea producerii lui este egala cu produsul dintre probabilitatea producerii lui si probabilitatea lui , dupa ce s-a produs

În conditiile de mai sus, numarul cazurilor posibile este limitat. De aceea, definitiile si probabilitatile de mai sus se refera la asa numita teorie a probabilitatilor discontinue, care se apropie de teoria probabilitatilor continue daca numarul cazurilor favorabile este destul de mare.

Probabilitatea evenimentului se noteaza si este un numar cuprins între 0 si 1, valoarea 0 corespunzând unui eveniment imposibil, iar 1 unui eveniment sigur.

Daca masurarea unei marimi se efectueaza, în conditii identice, de un numar mare de ori , obtinându-se siruri de valori aleatorii , iar din acestea, valori se afla în intervalul , probabilitatea

(2.10)

este o caracteristica a intervalului si se numeste frecventa relativa a variabilei în intervalul considerat.

Variabile aleatoare

Se numeste variabila aleatoare o marime reala care, în raport cu rezultatul unui experiment, poate lua orice valoare dintr-o multime bine definita de valori reale (domeniul de definitie al variabilei).

Variabilele aleatoare se clasifica dupa multimea pe care sunt definite. Astfel, se deosebesc variabile aleatoare de tip discret si de tip continuu.

Variabilele aleatoare discrete sunt definite pe o multime cel mult numarabila de evenimente. Numarul valorilor posibile ale unei variabile aleatoare discrete poate fi finit sau infinit.

Variabila aleatoare continua este definita pe o multime continua. Variabila aleatoare continua poate lua orice valoare între doua numere. Numarul valorilor posibile ale unei variabile aleatoare continua este infinit.

Functia de repartitie

Functia de repartitie a variabilei aleatoare se noteaza cu si este definita ca probabilitatea evenimentului

(2.11)

Din punct de vedere probabilistic, functia de repartitie caracterizeaza complet o variabila aleatoare, indiferent daca este vorba de o variabila aleatoare discreta sau continua.

Functia de repartitie (sau functia cumulativa a probabilitatilor) a unei variabile aleatoare discrete este suma probabilitatilor de la stânga punctului de abscisa (Fig. 2.1)

(2.12)

Se numeste repartitie a unei variabile aleatoare legea de probabilitate dupa care ea se produce. Repartitia unei variabile aleatoare discrete se scrie sub forma

sau

Fig. 2.1. Repartitia unei variabile discrete

Daca este o variabila aleatoare continua, functia de repartitie se defineste astfel (Fig. 2.2):

. (2.14)

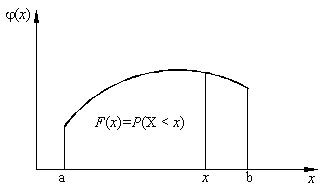
Fig. 2.2. Repartitia unei variabile continue

Functia de repartitie are urmatoarele proprietati:

1. Functia de repartitie este o functie monoton nedescrescatoare

, daca ; (2.15)

2. Pentru cea mai mica valoare posibila a variabilei aleatoare , functia de repartitie este egala cu zero

; (2.16)

3. Pentru cea mai mare valoare posibila a variabiei aleatoare , functia de repartitie este egala cu 1

; (2.17)

4. Functia de repartitie fiind o probabilitate, satisface dubla inegalitate

; (2.18)

5. Probabilitatea ca variabila aleatoare sa fie cuprinsa între si este egala cu diferenta dintre valorile functiei de repartitie la extremitatile intervalului, adica cu cresterea functiei în intervalul considerat

. (2.19)

Functia de repartitie a unei variabile discrete este o functie discontinua, în scara, admite salturi, salturile de la o treapta la treapta curenta sunt egale cu , suma tuturor salturilor fiind egala cu 1 (Fig. 2.3.a).

a) b)

Fig. 2.3. Functia de repartitie

Functia de repartitie a unei variabile aleatoare continue este, de asemenea o functie continua (Fig. 2.3.b, în care functia are drept asimptote dreptele si

Densitatea de repartitie

Se numeste densitate de repartitie (sau densitate de probabilitate) prima derivata - daca exista - a functiei de repartitie

.(2.20)

Densitatea de repartitie exista numai pentru variabile de tip continuu.

Probabilitatea ca variabila aleatoare continua sa ia valoare în intervalul este egala cu integrala densitatii de repartitie pe intervalul

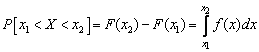, (2.21)

adica evenimentul este imposibil, iar este sigur.

Operatii cu variabile aleatoare

Fie si doua variabile aleatoare având repartitiile

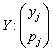
si (2.22)

Daca este o constanta reala, atunci este o variabila aleatoare având repartitia

(2.23)

Suma a doua variabile aleatoare si este o variabila aleatoare având repartitia

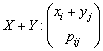
(2.24)

în care este probabilitatea realizarii simultane a evenimentelor si adica si

Produsul a doua variabile aleatoare si este o variabila aleatoare având repartitia

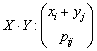
(2.25)

în care

si (2.26)

Densitatea de repartitie are proprietatile:

1. Densitatea de repartitie este nenegativa si aceasta rezulta din proprietatea functiei de repartitie de a fi nedescrescatoare,

2. Integrala densitatii de repartitie, în cadrul limitelor de variatie infinite, a variabilei aleatoare continue, este egala cu unitatea,

(2.27)

Valorile tipice ale variabilei aleatoare

O variabila aleatoare este caracterizata prin repartitia sa. Daca repartitia unei variabile nu este cunoscuta, pentru caracterizarea variabilei aleatoare se pot folosi anumite marimi numite valori tipice, asociate variabilei aleatoare.

Media

Prin definitie, valoarea medie (speranta matematica) a unei variabile aleatoare discrete cu repartitia (2.13) este egala cu suma produselor dintre valorile pe care le poate lua si probabilitatile corespunzatoare

(2.28)

Fie o variabila aleatoare de tip continuu si densitatea sa de repartitie. Media unei variabile aleatoare continue este definita de relatia

(2.29)

Daca variabila aleatoare este definita pe intervalul , atunci valoarea medie este

(2.30)

Mediana

Se numeste mediana a variabilei aleatoare , numarul care satisface ecuatia

(2.31)

sau

. (2.32)

Rezulta din ecuatia (2.32) ca mediana este solutia ecuatiei

(2.33)

Pentru o variabila aleatoare continua, mediana este data de ecuatia

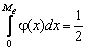(2.34)

Dispersia

Dispersia unei variabile aleatoare discrete reprezinta valoarea medie a patratului abaterii

(2.35)

sau

(2.36)

adica, diferenta dintre media patratului variabilei aleatoare si patratul mediei variabilei aleatoare.

Dispersia unei variabile aleatoare continue este media patratului abaterii lui

(2.37)

Abaterea medie patratica

Abaterea medie patratica a unei variabile aleatoare este radacina patrata a dispersiei acestei variabile aleatoare

. (2.38)

Dispersia si abaterea medie patratica sunt indicatorii cei mai utilizati pentru a caracteriza împrastierea valorilor unei variabile aleatoare.

Momente

Momentul simplu (initial) de ordinul k al unei variabile aleatoare discrete , calculat în raport cu originea abaterilor, care este zero, are expresia

(2.39)

Momentul simplu (initial) de ordinul 1 reprezinta media aritmetica

(2.40)

Folosind momentele simple, dispersia se poate exprima dupa cum urmeaza:

(2.41)

în care reprezinta momentul simplu de ordinul 2.

Momentul centrat de ordinul k al unei variabile aleatoare discrete , calculat în raport cu media aritmetica a variabilei aleatoare, este

(2.42)

Momentul centrat de ordinul 1 este zero, datorita proprietatii mediei aritmetice conform careia

(2.43)

Momentul centrat de ordinul 2 în raport cu media aritmetica este dispersia

(2.44)

Momentul ordinar de ordinul k, calculat în raport cu o valoare arbitrara , este media variabilei aleatoare

(2.45)

Momentul initial de ordinul al unei variabile aleatoare continue este

(2.46)

În particular, pentru se obtine valoarea medie a variabilei aleatoare continue

Momentul centrat de ordinul al unei variabile aleatoare continue este

(2.48)

În particular, pentru rezulta dispersia variabilei aleatoare continue

Momentul ordinar (conventional de ordinul este

(2.50)

Între momentele initiale si momentele centrate exista urmatoarele relatii:

(2.51)

(2.52)

Coeficientul de covarianta

Covarianta a doua variabile aleatoare si reprezinta momentul centrat mixt al celor doua variabile

(2.54)

Dezvoltând (2.54) se obtine formula echivalenta de calcul

(2.55)

Se numeste coeficient de covarianta raportul

(2.56)

în care sunt elementele matricei de covarianta, iar sunt numite corelatii.

Daca variabilele si sunt independente atunci , reciproca nefiind adevarata. Daca exista, atunci . Inegalitatea este o consecinta a inegalitatii lui Schwarz [ ].

Proprietatile valorilor tipice ale variabilei aleatoare

Proprietatile mediei

Media unei variabile aleatoare are proprietatile:

1. Daca este o constanta , atunci

(2.57)

2. Daca este o variabila aleatoare si si doua constante, atunci valoarea medie a variabilei aleatoare este egala cu

(2.58)

3. Daca si sunt doua variabile aleatoare independente având valorile medii si respectiv, , atunci valoarea medie a variabilei aleatoare exista si este egala cu

(2.59)

4. Daca si sunt doua variabile aleatoare independente pentru care exista valorile medii si respectiv, atunci valoarea medie a variabilei aleatoare exista si este egala cu

(2.60)

5. Daca este o variabila aleatoare a carei valoare medie exista, atunci variabila aleatoare se numeste abatere de la valoarea medie.

Proprietatile dispersiei

Dispersia unei variabile aleatoare are proprietatile:

1. Fie o variabila aleatoare cu dispersia ; atunci oricare ar fi numerele reale si , dispersia variabilei aleatoare este

(2.61)

2. Daca si sunt doua variabile aleatoare independente având dispersiile , respectiv , atunci pentru oricare doua constante , dispersia variabilei este

(2.62)

3. Daca este o variabila aleatoare având dispersia si o constanta reala, atunci

(2.63)

egalitatea având loc doar pentru

4. Pentru orice variabila aleatoare are loc inegalitatea Cebîsev [ ]

arbitrar.    (2.64)

Functii derivate

Se numeste functie caracteristica a variabilei aleatoare , valoarea medie a unei noi variabile aleatoare, obtinute din , înlocuind argumentul prin , unde este unitatea imaginara, iar - un parametru real.

Daca variabila este distribuita discret atunci functia caracteristica este data de relatia

(2.65)

Daca variabila are distributie continua cu desinatea atunci functia caracteristica este

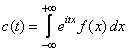(2.66)

Daca repartitia variabilei este de tip continuu, densitatea sa de repartitie este data de relatia

(2.67)

Functia de supravietuire sau de fiabilitate reprezinta probabilitatea ca o variabila aleatoare sa ia o valoare mai mare decât

(2.68)

Functia hazard sau rata cedarii a unei variabile este definita ca raportul dintre densitatea de repartitie si functia de supravietuire:

(2.69)

(2.70)

sau

(2.71)

Functia generatoare a unei variabile aleatoare care ia numai valori întregi pozitive este definita de relatia

(2.72)

Între funtia caracteristica si functia generatoare exista relatia

(2.73)

Functia caracteristica se utilizeaza pentru calculul mometelor factoriale, obisnuite si centrate de diferite ordine.

Indicatori statistici

Indicatorul statistic reprezinta expresia numerica a unei trasaturi observate pe o colectivitate definita în timp si spatiu.

În functie de metoda obtinerii indicatorilor si de rolul jucat în cercetarea statistica, indicatorii pot fi împartiti în doua categorii: (a) indicatori absoluti (primari); (b) indicatori derivati (secundari).

Indicatorii absoluti sunt rezultatul observarii si sistematizarii datelor; în consecinta acestia reflecta dimensiunea, marimea, amplitudinea fenomenului în unitati concrete, specifice, de masura.

Indicatorii derivati se obtin în procesul de calcul statistic si reflecta într-o maniera abstracta, aspecte calitative, evolutive ale colectivitatii cercetate. Dintre indicatorii derivati amintim: marimile relative si marimile medii, indicatorii variatiei si ai asimetriei, indicii statistici, parametrii functiilor de regresie si ajustare analitica etc.

Functiile indicatorilor statistici sunt: de masurare, de comparare, de sinteza, de estimare, de verificare a ipotezelor statistice, de testare a semnificatiilor parametrilor statistici utilizati.

Orice indicator statistic trebuie sa îndeplineasca doua conditii: (a) sa aiba un continut stiintific bine determinat, o definitie sau o formula a sa; (b) sa indeplineasca conditia de compatibilitate.

Indicatorii tendintei centrale

Principali indicatori ai tendintei centrale sunt: (a) indicatorii medii de control: media aritmetica, media geometrica, media armonica etc; (b) indicatorii medii de pozitie: modul, mediana, cuartilele si decilele.

Media aritmetica

Media este expresia sintetizarii într-un singur nivel reprezentativ a tot ce este esential, tipic si obiectiv în aparitia, manifestarea si dezvoltarea unei variabile (caracteristici) [1].

Functie de natura datelor înregistrate si de natura variatiei, media poate fi: media aritmetica (simpla), media armonica, media geometrica, media patratica, media cubica, media parabolica, media cronologica etc.

Media aritmetica simpla de sondaj (sau de selectie) a unui sir de valori se calculeaza cu relatia

(2.74)

Media aritmetica ponderata a unui sir de valori se calculeaza cu relatia

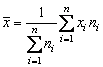(2.75)

în care reprezinta frecventa sau numarul de aparitii al variabilei

Media aritmetica ponderata este influentata atât de nivelul caracteristicii cât si de nivelul frecventei.

Media aritmetica este o valoare interna a seriei din care a fost calculata (trebuie sa fie mai mare decât valoarea minima si mai mica decât valoarea maxima),

Principiul pe care se bazeaza media este cel al compensatiei abaterilor (+ sau -); suma abaterilor nivelurilor individuale ale variabilei aleatoare fata de media lor diind egala cu zero.

Media armonica

Media armonica reprezinta acea valoare care înlocuid termenii reali din colectivitate nu modifica suma inverselor. Media armonica este o valoare interna seriei din care a fost calculata. Se disting doua cazuri:

- Media armonica simpla

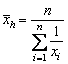; (2.76)

Media armonica ponderata

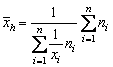. (2.78)

Când nu se cunosc frecventele se foloseste media armonica special ponderata. Ponderarea nu se face cu ci cu . În acest caz, media armonica este un artificiu de calcul pentru a determina media aritmetica când datele nu permit aflarea directa a acesteia

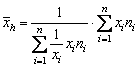(2.79)

Media geometrica

Media geometrica este acea valoare care înlocuid termenii reali din colectivitate nu modifica produsul acestora. În cazul mediei geometrice functia determinanta este de tip multiplicativ si se disting doua cazuri:

- Media geometrica simpla (neponderata)

sau , (2.80)

- Media geometrica ponderata

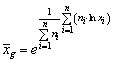. (2.81)

Media geometrica nu este influentata nici de valorile cele mai mici, nici de valorile cele mai mari, dar nu poate fi determinata daca unele valori sunt nule sau negative. Media geometrica se utilizeaza pentru calculul indicelui mediu de crestere sau descrestere.

Media patratica

Se foloseste când nivelul variabilei prezinta cresteri din ce în ce mai mari, modificându-se aproximativ dupa o functie exponentiala. Se disting doua cazuri:

- Media patratica simpla

; (2.82)

- Media patratica ponderata

.

Media patratica se poate calcula si pentru variabile nule sau negative. Media geometrica este sensibila la variatii mari care prin ridicare la patrat devin foarte mari.

Într-o serie statistica în care se pot calcula toate mediile exista relatia

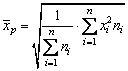(2.84)

Media cronologica

Media cronologica este utilizata pentru determinarea nivelului mediu al seriilor cronologice de momente. Media cronologica este o medie care are la baza principiul de calcul al mediei aritmetice.

Daca intervalele de timp care separa termenii seriei cronologice sunt egale, se calculeaza media cronologica simpla

(2.85)

Daca intervalele de timp dintre termenii seriei cronologice de momente sunt neegale atunci se calculeaza media cronologica ponderata. În acest caz, mediile partiale din care se calculeaza media întregii perioade sunt ponderate cu durata perioadelor partiale cuprinse între termenii seriei dupa formula

(2.86)

Media progresiva

Media progresiva reprezinta o medie a timpilor de nivel calitativ superiori în cadrul colectivitati date. Media progresiva se calculeaza cu relatia

(2.87)

în care este media generala a seriei, iar - media termenilor calitativ superiori mediei generale.

Mediana

Mediana este acea valoarea a caracteristicii fata de care frecventa valorilor mai mica decât ea este egala cu frecventa valorilor mai mari decât ea, deci mediana împarte sirul de date în doua parti egale. Din punct de vedere analitic, mediana corespunde valorii abscisei pentru care ordonata împarte suprafata delimitata de curba de repartitie în doua parti egale.

Daca sirul de date este constituit dintr-un numar impar de valori , mediana este reprezentata de valoarea de rang . În cazul în care sirul de date este constituit dintr-un numar par de valori , mediana se situeaza între doua valori mediane si n general, s-a convenit sa se considere ca mediana media aritmetica a celor doua valori mediane:

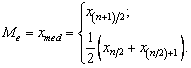
Mediana unei functii de repartitie este valoarea pentru care valoarea mai mare si mai mica a lui au probabilitati egale

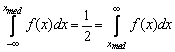(2.89)

În cazul seriilor de distributie, mediana se determina cu formulele:

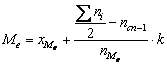, unde este numar par; (2.90)

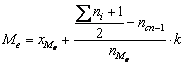unde este numar impar, (2.91)

în care: este limita inferioara a intervalului median; - frecventele caracteristicii - marimea intervalului; - frecventa intervalului median; - marimea intervalului.

Modul

Modul este, prin definitie, valoarea caracteristicii cu frecventa cea mai mare de aparitie în colectivitate. Modul mai poate fi definit ca valoarea caracteristicii careia îi corespunde densitatea maxima de repartitie. Minimul densitatii de repartitie este antimod. Daca sirul de masuratori are doua valori maxime, repartitia se numeste bimodala, iar daca sunt mai multe, plurimodala.

Modul unei functii de repartitie este valoarea lui pentru care functia are un maxim. Intervalul modal este intervalul cu frecventa cea mai mare.

În cazul seriilor de distributie, modul se calculeaza cu relatia

(2.92)

unde: este limita inferioara a intervalului modal; - diferenta dintre frecventa intervalului modal si frecventa intervalului premodal (anterior); - diferenta dintre frecventa intervalului modal si frecventa intervalului postmodal (urmator); - marimea intervalului modal.

K. Person [ ] a stabilit o expresie care da valoarea modului în functie de media aritmetica si mediana pentru toate repartitiile unimodale

(2.93)

Media, mediana si modulul caracterizeaza tendinta centrala si forma de variatie a caracteristicii. În cazul unei distributii simetrice ele coincid.

Valoarea centrala a sirului

Valoarea centrala a sirului de date este

(2.94)

în care este valoarea cea mai mare dintre valorile , iar , cea mai mica.

Cuantilele

Cuantilele sunt valori ale caracteristicii care împart seria în parti egale. Ele descriu pozitia anumitor termeni în cadrul seriilor statistice. Functie de valorile lui , cuantilele se numesc: mediana, ; cuartile, ; decile, ; centile,

Cuartile

Cuartilele sunt marimi de pozitie în seriile statistice. Cuartilele, în numar de trei, împart seria în patru parti de frecvente egale cu 1/4

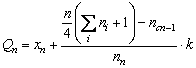(2.95)

unde este limita inferioara a cuartilei - frecventa cumulata pâna la intervalul - frecventa intervalului - marimea intervalului în care se afla cuartila

Cuartila centrala a seriei se noteaza cu , ea reprezentând valoarea unitatii mediane. Ordonata corespunzatoare acestei unitati împarte aria delimitata de curba distributiei în doua parti egale. Cuartila inferioara este unitatea mediana a valorilor situate în partea inferioara a medianei , iar cuartila superioara este mediana valorilor situate în partea superioara a medianei propriu-zise.

Locul unei cuartile oarecare este dat de relatia

(2.96)

Decilele

Decilele, în numar de noua, împart seria în zece intervale de frecvente egale cu 1/10

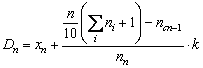(2.96)

unde este limita inferioara a decilei - frecventa cumulata (suma frecventelor anterioare) pâna la intervalul - frecventa intervalului - marimea intervalului în care se afla decila

Locul unei decile oarecare este dat de relatia

(2.96)

Centilele

Centilele, în numar de 99, împart seria în 100 de intervale egale

(2.97)

unde este limita inferioara a centilei - frecventa cumulata pâna la intervalul - frecventa intervalului - marimea intervalului în care se afla centila

Indicatorii de masura a împrastierii

Dispersia

Dispersia (sau varianta) sirului de date, denumita si dispersie de sondaj (esantion) este indicatorul de baza al împrastierii.

Pentru o serie simpla, dispersia se calculeaza cu formula

(2.98)

Pentru o serie de frecvente variate, dispersia se calculeaza cu formula

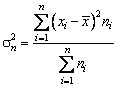(2.99)

Dispersia de sondaj se poate folosi ca estimatie a dispersiei din populatia originara (dispersie de selectie), considerându-se relatia

(2.100)

Abaterea medie patratica

Pentru o serie simpla, abaterea medie patratica (sau deviatia standard de sondaj; abaterea standard) se calculeaza cu formula

(2.101)

Pentru o serie de frecvente variate, abaterea medie patratica se calculeaza cu formula

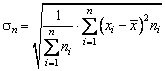(2.102)

Abaterea medie patratica a populatiei originara este

Abaterea medie liniara

Abaterea medie liniara (sau abaterea medie absoluta) se calculeaza ca media aritmetica din valorile absolute ale abaterilor variantelor caracteristicii fata de media acestor variante.

Abaterea medie liniara se foloseste pentru a caracteriza omogenitatea colectivitatii statistice.

Coeficientul de variatie

Coeficientul de variatie al sirului de date se calculeaza ca raportul dintre abaterea medie patratica si media aritmetica a sirului de date

. (2.106)

Coeficientul de variatie ia valori începând cu 0. Daca este pâna în 35% se considera ca intensitatea variatiei este redusa, colectivitatea este omogena si media este reprezentativa. Daca depaseste 35% se considera ca intensitatea variatiei creste si colectivitatea este eterogena iar media tinde sa fie o marime nereprezentativa.

Abaterea medie intercuartilica

Abaterea medie intercuartilica este definita ca jumatatea intercuartilei

(2.107)

Intercuartila este o masura a dispersiei exprimata prin diferenta dintre cuartila superioara si cea inferioara.

Abaterea medie intercuartilica este folosita în analiza dispersionala si are avantajul ca poate fi usor calculata. Abaterea medie intercuartilica reprezinta aproximativ din abaterea standard si este mai putin exacta decât abaterea medie liniara. Având în vedere ca se exprima în aceeasi unitate de masura ca si variabila analizata, abaterea medie intercuartilica nu se poate utilize pentru comparatii între serii statistice diferite din punct de vedere al unitatilor de masura.

Coeficientul de variatie intercuartilica

Coeficientul de variatie intercuartilica este rapotrul dintre semiintercuartila si mediana

(2.108)

Coeficientul de variatie intercuartilica prezinta avantajul unei comparabilitati mai largi.

Amplitudinea

Amplitudinea variatiei exprima marimea câmpului de împrastiere în jurul mediei.

Amplitudinea absoluta este diferenta dintre valoarea cea mai mare si valoarea cea mai mica a sirul de date

(2.109)

Amplitudinea se poate calcula si ca marime relativa. Amplitudinea relativa este raportul dintre amplitudinea absoluta si media aritmetica a sirului de date

(2.110)

Amplitudinea variatiei are aplicatie în studiul statistic al calitatii productiei.

Momente

Momentele sunt acele valori care caracterizeaza o repartitie si permit precizarea anumitor caracteristici ale repartitiei. Exista mai multe tipuri de momente:

Pentru serii simple, momentul simplu de ordinul are expresia

(2.111)

Pentru serii de distributie, momentul simplu se calculeaza cu relatia

(2.112)

Momentul centrat de ordinul , pentru serii simple, are expresia

(2.113)

Pentru serii de distributie, momentul centrat are expresia

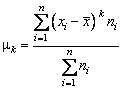(2.114)

Pentru serii simple, momentul ordinar de ordinul , calculat în raport cu o valoare arbitrara , are expresia

(2.115)

Pentru serii de distributie, momentul ordinar are expresia

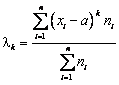(2.116)

Indicatorii asimetriei

Coeficientul de asimetrie

Pentru caracterizarea seriilor de distributie unidimensionale si unimodale este necesara cunoasterea gradului de oblicitate, de îndepartare a acestor distributii de la simetrie, aspect denumit asimetrie.

Pentru cuantificarea gradului de asimetrie se foloseste coeficientul de asimetrie definit de relatia

(2.117)

sau în functie de momentele centrate

(2.118)

în care este momentul centrat de ordinul trei, iar este momentul centrat de ordinul doi.

De asemenea, coeficientul de asimetrie poate fi definit ca diferenta dintre medie si mod

. (2.119)

Daca: atunci exista simetrie perfecta; exista asimetrie pozitiva sau de stânga; exista asimetrie negativa sau de dreapta.

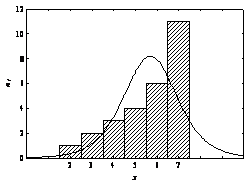
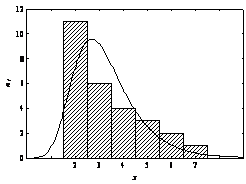
a) b)

Fig. 2.4. Distributii asimetrice:

a) asimetrie negativa; b) asimetrie pozitiva.

Pentru masurarea asimetriei se foloseste cel mai des coeficientul de asimetrie Pearson [ ] definit de relatia

(2.120)

în care este modulul; - abaterea medie patratica; - media aritmetica.

Daca repartitia prezinta o asimetrie negativa. Daca repartitia este simetrica. Daca repartitia prezinta o asimetrie pozitiva. Pentru repartitii moderat asimetrice

Coeficientul de asimetrie determinat pe baza metodei Fisher [ ] are expresia

(2.121)

în care reprezinta mediana.

Coeficientul de asimetrie are valori între -3 si +3; cu cât se apropie de zero cu atât sirul este mai simetric.

Coeficientul de asimetrie determinat pe baza cuartilelor are expresia

(2.122)

Coeficientul de asimetrie determinat pe baza centilelor are expresia

(2.123)

Coeficientul de boltire

Coeficientul de boltire se calculeaza ca raport între momentul centrat de ordinul patru si patratul momentului centrat de ordinul doi

în care:

(2.125)

(2.126)

Coeficientul de boltire este un indicator al pantei curbei densitatii de repartitie, în vecinatatea modului de sondaj.

Curtozisul

Curtozisul arata gradul de concentrare al frecventelor în zona centrala a distributiilor unimodale. Pentru determinarea curtozisului se foloseste coeficientul de boltire.

stiind ca pentru repartitia normala si considerând aceasta valoare ca nivel standard în masurarea gradului de boltire al distributiei unimodale, curtozisul este dat de relatia

(2.127)

Daca , curba densitatii de repartitie se numeste leptocurtica si este mai ascutita la vârf decât curba normala. Daca repartitia se numeste platicurtica si are vârful mai plat decât o curba normala. Daca repartitia se numeste normala sau mezocurtica.

Curtozisul se poate determina si cu ajutorul cuartilelor si al centilelor cu relatia

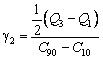(2.128)

Se pot utiliza urmatoarele functii Excel:

1. AVERAGE - Media aritmetica.
2. MEDIAN - Mediana
3. MODE - Modulul
4. VARP - Variatia populatiei (se calculeaza numai daca avem in studiu o populatie)
5. VAR - Variatia de selectie
6. STDEVP - Abaterea standard a populatiei (se calculeaza numai daca avem in studiu o populatie)
7. STDEV - Abaterea standard de selectie
8. STDEV/AVERAGE - Coeficientul de variatie
9. QUARTILE- Cvartila 1,2,3,4 
10. AVEDEV - media deviatiei de la media aritmetica
11. DEVSQ - suma de patrate a deviatiilor valorilor de la media aritmetica
12. GEOMEAN- media geometrica
13. HARMEAN - media armonica
14. KURT- boltirea sau kurtosis-ul
15. MAX - maximul
16. MIN - minimul
17. PERCENTILE - returneaza a k-a percentila
18. SKEW - asimetria

daca CV este sub 10% atunci populatia poate fi considerata omogena;

daca CV este intre 10%-20% atunci populatia poate fi considerata relativ omogena;

daca CV este intre 20%-30% atunci populatia poate fi considerata relativ eterogena;

daca CV este peste 30% atunci populatia poate fi considerata eterogena.