MODELUL DE PIATA AL RENTABILITTATII SI RISCULUI VALORILOR MOBILIARE

MODELUL DE PIATA AL RENTABILITTATII SI RISCULUI VALORILOR MOBILIARE

Preocuparea cotidiana a investitorilor financiari si a gestionarilor prtofoliilor de titluri este de a anticipa tendintele de crestere sau de scadere ale indicelui general al pietei bursiere. De aceste tendinte este legata evolutia valorii de piata a fiecarui titlu din portofoliu. Fiecare valoare mobiliara urmareste, mai mult sau mai putin, tendintele pietei. Cand indicele pietei este in crestere, majoritatea titlurilor au un curs crescator si invers in perioada de scadere. Sunt destul de rare valorile mobiliare care urca intr-o Bursa in scadere si invers. Anumite valori mobiliare sunt mai sensibile decat altele la miscarile pietei bursiere.

Aceasta relatie intre rentabilitatea realizata de o valoare mobiliara si rentabilitatea, ca indice general al valorilor mobiliare, este formalizata in cadrul conceptului de model de piata. Modelul de piata, in forma sa cea mai simpla, reprezinta relatia liniara ce poate exista intre ratele de rentabilitate constatate, intr-o perioada de timp, asupra unei actiuni sau asupra unui portofoliu de valori mobiliare si ratele de rentabilitate realizate in aceeasi perioa 151y2416b da, prin indicele general al pietei bursiere.

8.1. Componentele riscului valoriolr mobiliare

Surprinderea acestei caracteristici principale a titlurilor individuale, ca dde altfel a intregului portofoliu, se face prin utitlizare modelului de piata, care este unul dintre primele modele de determinare a rentabilitatii si riscului investitiilor in valori mobiliare. Ideea centrala a modelului de piata eficienta este aceea ca fluctuatiile de curs ale valorilor mobiiare sunt inflluentate, in general, de modificarile indicelui general al bursei de valorisi, in particular, de modificarile in conditiile specifice ale societatilor emmitente ale titlurilor.

Variabilitatea totala a rentabilitatii unei valori mobiliare se imparte in doua parti:

(1) - o parte determinata de influenta pietei bursiere, parte care determina riscul sistematic, numit si risc nediversificabil = risc de piata;

Acest risc este legat de variabilitatea principalilor indicatori macroeconomici:

produsul intern brut (PIB);

rata inflatiei;

rata medie a dobanzii;

cursul valutar etc.

Variabilitatea acetor indicatori macroeconomici induce o influenta mai mare sau mai mica asupra rentabilitatii titlurilor. Marimea acestei influente este determinata de marimea dependentei activitatii intreprinderii emitente de conditiile mediului economic national.

(2) - o parte determinata de influenta caracteristicilor specifice fiecarui titlu, parte care determina riscul specific sau diversificabil. In opozitie cu riscul de piata, acesta se mai numeste risc nesistematic sau undividual.

Riscul specific poate fi impartit, el insusi, in:

(2.1) - risc specific fiecarui titlu, determinat de modificarile in comportamentul economic al intreprinderii care l-a emis.

Asa cum se va vedea in capitolele de analiza financiara, riscul specific intreprinderii emitente se refera la variabilitatea rentabilitatii economice, determinata de ponderea cheltuielilor fixe in cifra de afaceri (risc economic, operational), la variabilitatea rentabilitatii financiare, determinata de ggradul de indatorare (risc financiar) si la variabilitatea trezoreriei nete, datorata gestitunii echilibrului financiar (pe termen lung, pe termen scurt si, in general, de imposibilitatea onorarii datoriilor contractate = risc de faliment).

(2.2) - risc specific ramurii industriale de care apartine intreprinderea emitenta.

Este vorba de pozitia ramurii (sectorului) industriale pe piata interna si internationala privind cererea pentru produsele si serviciile ramurii, privind sursele de aprovizionare, privind motivatia personalului ramurii, privind implicarea statului in sustinerea ramurii etc.

Se demonstreaza usor (prin Legea numerelor mari) ca partea de risc specific se reduce corespunzator pe masura ce se diversifica portofoliul de valori mobiliare prin adaugarea de noi titluri. Este cunoscutul avantaj al diversificarii titlurilor detinute .

In ceea ce priveste riscul sistematic, acesta nu este majoritar in influentarea variatiilor de curs ale titlurilor, el ocupa in medie, o pondere de 33% in cazul valorilor mobiliare franceze, 30% in cazul celor americane si 41% pentru cele britanice. Pe de alta parte, fiecare intreprindere raspunde in mod diferit la miscarile pietei in functie de gradul ei de īndatorare, de structura costurilor, de stabilitatea beneficiilor, de pozitia ei pe piata concurentiala etc.

8.2. Modelul liniar al rentabilitatii titlurilor

Relatiadintre rentabilitatea indilviduala a titlurilor si rentabilitatea generala a pietei (rata medie a dobānzii de piata, rentabilitatea indicelui general al valorilor mobiliare) este atat de evidenta (statistic), īncat este preluata ca un postulat de baza al teoriei flnanclare. Pornind de la aceasta evidenta, cercetatorii financiari au fost preocupati de masurarea acestei relatii si testarea generalizarii ei.

Modelul de piata, datorat cercetarilor profesorului William Sharpe, īn forma sa simpla, reprezinta relatia 1iniara dintre rentabilitatea individuala a titlurilor sau a portofoliilor de titluri, pe de o parte, si rentabilitatea generala (indicele general) al pietei bursiere, pe de alta parte (one-factor model, in engleza).

Figura 8.1. Metoda grafica de reprezentare a modelului de piata

Prin metoda grafica a reprezentarii punctelor de intersectie dintre rentabilitatile titlurilor indivlduale si rentabilitatea generala a pietei, se poate vizualiza functia de regresie a acestor variabile (vezi fig. 8.1.). In continuare, prin metoda celor mai mici patrate, se pot determina parametrii a si b ai functiei de regresie. Acesti parametri vor trasa traiectoria curbei functiei, astfel īncat sa se obtina cele mai mici patrate ale diferentelor īntre punctele de intersectie si valorile functiei. Metoda celor mai mici patrate, a lui Gauss, aproximeaza cel mai bine valorile functiei, īntrucat, īn conformitate cu legea repartitiei normale, cele mai mici diferente fata de medie au cele mai mari probabilitati de realizare (pentru valori mai mici, probabilitatile sunt cele mai mari).

Functia care aproximeaza corelatia dintre variabilitatea rentabilitatilor individuale ale unei actiuni si variabilitatea rentabilitatii generale a pietei este o dreapta, numita si dreapta de regresie. Panta acestei drepte sau coeficientul ei unghiular semnifica volatilitatea actiunii, respectiv sensibilitatea rentabilitatii el la modificarile rentabilitatii generale a pietei. Imprastierea punctelor de intersectie fata de dreapta de regresie da masura caracterului sistematic (de piata) sau nesistematic (specific) al riscului de variatie a rentabilitatii titlului: cu cat punctele individuale de intersectie se afla mai aproape de dreapta de regresie, cu atat riscul sistematic va avea o pondere mai mare si invers.

Ecuatia dreptei care, statistic, ajusteaza cel mai bine punctele de variatie are

urmatoarea expresie (a se vedea si fig. 8.1.):

R_i = a_i b_i R_M +e_i

īn care:

R_i = rata rentabilitatii, estimata pentru titlul i;

a_i = parametru al functiei, egal cu marimea R_i atunci cand R_M = 0;

b_i = coeficient de regresie, de volatilitate sau coeficient beta (pe scurt, "beta");

R_M = rata rentabilitatii pe piata, masurata prin indicele general de bursa;

e_i = parametru specific titlului "i", prin care se masoara riscul individual.

8.3. Volatilitatea titlurilor individuale

Cel mai important dintre parametrii functiei de regresie este coeficientul beta, care exprima rentabilitatea marginala a titlului "i", īn raport cu variatia rentabilitatii generale pe piata bursiera. Estimarile coeficientilor beta, pentru flecare titlu īn parte, au o anumita doza de aproximare, mai mare sau mai mica. De aceea, cea mai buna estimare se face pentru un portofoliu de titluri unde au loc compensari (conform legii numerelor mari).

Se porneste de la ipoteza constantei īn timp a coeficientilor beta. In consecinta, estimarea rentabilitatii sperate R_i porneste de la un beta deja calculat si care se presupune ca ramāne constant īn perioada urmatoare. Practica dovedeste īnsa ca acesti coeflcienti sunt modificabili īn timp. Nefiind alta posibilitate de estimare, se pastreaza beta calculat anterior ca o marime de referinta determinata pe seama variabilitatii anterioare atāt a R_i, cat si a R_M .

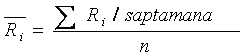
Coeficientii beta se determina pe baza observatiilor asupra rentabilitatilor saptamānale privind tltlul "i" si portofoliul de piata (indicele bursier = M). In consecinta, mediile acestor rentabilitati vor fi:

unde n = nr. de saptamani observate

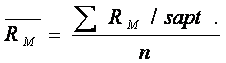
Pentru relevanta coeficientului beta, observatiile asupra lui R_i si R_M se fac pe o perioada anterioara de minimum doua ori mai mare decat orizontul de estimare a rentabilitatilor viitoare.

Aflarea coeficientului beta se face prin metoda celor mai mici patrate. Minimul patratelor diferentelor se obtine in punctele īn care derivata functiei s_i , īn raport cu R_M, este egala cu 0:

Din calculul derivatei si prin egalarea ei cu 0 se determina beta:

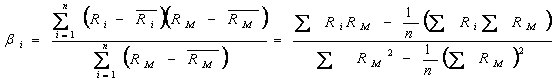
Exemplu: Se foloseste o baza de date formata din rentabilitatile medii trimestrlale ale titlului "i" si ale indicelui general al pietei. Analize mai pertinente ale acestei corelatii se vor face, asa cum am afirmat mai sus, pe baza rentabilitatilor saptamānale, sau cel putin pe baza rentabilitatiior lunare.

Asadar, īn tabelul 8.1. se prezinta cele doua serii de date si calcule premergatoare aflarii coeficientului beta si ale celorlala1ti parametri ai functiei.

Tabelul 8.1.

In aceste conditii, coeficientul beta se calculeaza astfel:

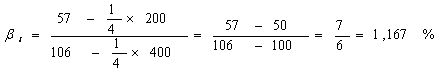
Cu cat coeficientul b este mai ridicat, cu atat riscul sistematic de piata al titlului va fi mai mare.

In raport cu b, titlurile se clasifica īn:

1) - titluri volatile (foarte volatile) cu beta b > 1, care semnifica faptul ca o

variatie de 1% a indicelui general a1 pietei bursiere (R_Ml - R_MO = 1%) determina o variatie mai mare de 1% a rentabilitatii titlului "i" (R_i1 - R_io > 1%). In exemplul nostru, titlul analizat are o volatilitate ridicata: la o variatie a rentabilitatii pietei cu 1%, rentabilitatea titlului se modifica cu

Fig. 8.2. Titlurl foarte volatile

0 astfel de volatilitate se inregistreaza, de regula, la titlurile emise de intreprinderi de produse chimice, de sticlarie, de, echipamente electrice si electronice, de aparate casnice, de automobile etc. Sunt deci ramuri industrlale producatoare de bunuri de consum, cu o sensibilitate mai mare īn raport cu comportamentul cumparatorilor din, randul populatiei.

2) - titluri putin volatile cu    beta b < 1 care exprima o variabilitate mai mica a rentabilitatii titlului "i" determinata de variatia rentabilitatii de piata, deci pentru DR_M = DR_i< 1%. Aceasta volatilitate redusa poate fi īntalnita, de regula, la titlurile īntreprinderilor producatoare de material rulant, de locuinte, la societatile de asigurari.

Fig. 8.3. Titluri putiN volatile

3) - titluri cu b = 1, pentru care o variatie a rentabilitatii generale antreneaza

aceeasi variatie a rentabilitatii titlului "i". Astfel de volatilitati direct proportionale pot fi īntilnite īn societati de tip holding, īn īntreprinderi de constructii industriale, de textile- īncaltaminte, īn banci si societati de credit etc.

In general, coeficientul beta are valori pozitive b > 0 . Pentru societatile de asigurari si minele de aur se poate īnregistra un beta negatlv (b < 0) , semnificand o influenta inversa a rentabilitatii titlurilor acestor societati asupra rentabilitatii generale a titlurilor financiare pe piata bursiera.

Deci coeficientul beta al volatilitatii titlului "i", este egal cu "covariatia" (s_iM) ratelor rentabilitatii titlului "i" cu cele ale pietei bursiere, raportata la dispersia indicelui general al pietei titlurilor.

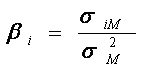
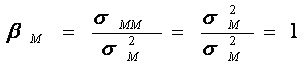
Covariatia rentabilitatilor pietei bursiere cu ele īnsele (s_MM) este chiar dispersia acestora (s_M ). In consecinta, coeficientul beta al pietei bursiere este egal cu 1 :

Coeficientul beta al titlurilor individuale exprima deci cantitatea de risc sistematic (de piata) al titlurilor: de cāte ori covariatia rentabilitatii acestora cu rentabilitatea de piata este mai mare (sau mai mica) decāt riscul de piata (s_M ) . Spre exemplu, un beta egal cu doi exprima un risc de piata dublu al titlului respectiv īn raport cu riscul pietei financiare.

Parametrul alfa a_i) al functiei de regresie se obtine din acelasi sistem de ecuatii rezultat prin metoda celor mai mici patrate si utilizat pentru calculul coeficientului beta (b) sau dln relatia care verifica rentabilitatea medie

individuala:

īn care e_i = 0 prin definitie

3..5. Intensitatea corelatiei dintre rentabilitatea titlurilor si

rentabilitatea pietei bursiere

Pentru o estimare fiabila a riscului de piata este necesara o testare a intensitatii corelatiei care conduce la determinarea coeficientului beta. Masurarea statistica a acestei intensitati o putem avea prin doi indicatori: coeficientul de corelatie (r) si patratul acestuia (R²).

Coeficientul de corelatie (r) exprima gradul de determinare a rentabilitatii titlului "i" de catre rentabilitatea pietei bursiere "M".

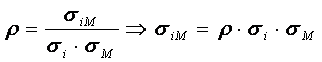
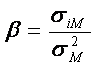
Unde r_iM = covarianta

Cum īnsa

putem exprlma pe b īn functie de coeflcientul r

si invers

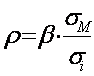
Pentru valori pozitive (0 < r < 1) coeficientul releva o dependenta direct proportionala īntre rentabilitatile "i"si "M". Valoarea 1imita egala cu 1 (r = 1) semnifica o corelatie strict pozitiva, respectiv īntreaga variatie a rentabilitatii titlului "i" este determinata de variatia rentabilitatii de piata "M" si īn aceeasi proportie. In acest caz riscul specific nu exista, singurul care se

manifesta este riscul de piata.

Pentru valori nule, coeficientul r evidentiaza o 1ipsa de corelatie īntre rentabilitatile "i" si "M", respectiv o independenta a determinarilor acestora. Pentru titlul "i", singurul risc care se manifesta este riscul specific (riscul de piata este egal cu zero).

Valorile negative (-l r < + 0 ) ale coeficlentului r releva o dependenta invers

proportionala īntre rentabilitatea "i" si "M". Valoarea limita egala cu -1 (r = -1) semnifica o corelatie strict negativa care elimina de asemenea riscul specific. Diferenta fata de corelatia strict pozitiva consta īn faptul ca variatia rentabilitatii "M" determina aceeasi variatie dar īn sens invers a rentabilitatii "i".

Coeficientul R² exprima proportia īn care variabilitatea rentabilitatii titlului "i" este explicata (determinata) prin modelul (liniar) de piata:

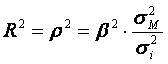
3.7. Variabila e ca masura a riscului specific

Revenind la modelul (liniar) de piata, suntem acum īn masura sa identificam proportia sistematica (datorata evolutiei de ansamblu a pietei) si proportia specifica aferente rentabilitatii si riscului titlului individual "i".

rentabilitatea legata de

evolutia pietei

rentabilitatea legata de

evolutia intreprinderii

risc sistematic risc specific

Prin interpolare putem identifica proportia sistematica a rentabilitatii titlului individual (R_i^*):

In aceste conditii, variabila e_i din modelul de piata se obtine ca diferenta intre rentabilitatile efective (R_it) si cele estimate mai sus (R_it ^*):

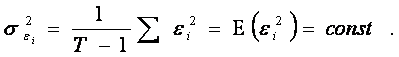
Din relatia de mai sus deriva si denumirea de variabila reziduala atribuita termenului e_i. Media acestei variabile aleatoare este zero si deci, prin extrapolare, speranta matematica a acesteia este zero. Din acelasi motiv ( e_i = 0), dispersia variabilei reziduale (s _ei ) este egala cu media (respectiv speranta matematica) a patratului acesteia:

Definind componenta speciflca a rentabilitatii si cea a riscului titlului "i", este evident faptul ca variabila e_i este independenta de evolutia rentabilitatii "M". In consecinta, covariatia (s_ei,M) dintre s_et si R_Mt si coeficientul lor de corelatie (r_ei, M) sunt egale cu zero:

Independenta dintre R_M si e_i, ca variabile ale modelului de piata, explica atunci si relatia de calcul a dispersiei totale

ca dispersie a sumei a doua variabile aleatoare independente (teorema de aditivitate a dispersiei).

Figura 3.4. Reprezentarea grafica a componentelor riscului unul titlu financiar

Grafic, riscul total al titlului "i" se poate explica si prin intermediul teoremei lui Pitagora (vezi figura 3.4.).

Independenta variabilei e_i se manifesta, de asemenea, fata de variabilele e_j ale altor titluri (j i): s_{ei ,ej} r_{ei ,ej}

Capitolul 9

EVALUAREA si GESTIUNEA PORTOFOLIILOR

speram ca cltltorul atent 81 demersulul nostru explicativ prIvlnd teorla flnanaelor 8

retlnut ca cercetarea performantel Investltlonale se face īn cadrul crlteriulul ren-

tabllltate-risc. rn conseclnta, evaluarea si gestlunea eflclenta 8 portofliulul se vor

anallza si antlclpa īn cadrul acelulasi crlteriu rentabllltate-risc.

fntruc§t orlce portofoliu se constitule dlntr-o anumlta comblnatie de tltlurl flnanclare,

este natural sa regaslm la nIvelul portofliulul aceleasi caracteristicl ale performantel

tltlurllor: caracterul aleatorlu al rentabilitatii, componenta slstematlca Cde piata) si cea

speclflca Ccomblnatiei de tltlurl) a rentabilitatii si a risculul etc. Daca īntr-un caz par-

tlcular rentabilltatea si riscul unul portofoliu colncld cu cele ale unul tltlu, atunciputem

Inversa sensul anallzel. Putem sa aflrmam astfel ca flecare tltlu financlar nu este

altceva decat 0 combinatie speclflca a portofliulul de piata Cmai mult sau mai putln

dlversiflcat).

Oblectlvul urmarit īn acest capitol prlveste performanta portofliulul ca 0 comblnatie

de titlurl. vom analiza īntr-un capitol urmator CCAPM) Impllcatlile unul portofoliu de piata

eflclent asupra rentabllltatli flecarul titlu Indlvldual. rn acest capltol ne Intereseaza

mod deoseblt comblnatlile eficiente de tltlurl (portofolllle situate pe frontiera eflclenta)

care sa satlsfaca functla de utilitate a Investitorilor, respectiv atitudlnea lor fata de risc.

0 data definita frontiera eflclenta, putem determlna portofliul optim, respectlv por-

tofoliul cu dlspersie (varlanta) mlnlmaia care sa satisfaca functla de utilitate 8 unul

Investltor cu averslune fata de risc.

At§t portofolllle eflciente c§t si cel optim sunt poslblle pe orlce piata flnanclara

īntruc§t: .

Cl) : exlsta 0 proportionalltate dlrecta īntre riscul asumat

pentru 0 Investltie financfara: comportament ratlonal Impllclt;

C2) exlsta 0 corelatie pozltiva īntae rentabilitatiie tltlurllor, flecare cu flecare si flecare

cu ansamblul titlurllor (respectiv cu portofliul de piata);

C3) evolutla pretulul de piata 81 titlurilor si a rentabilitatiior urmeaza 0 tralectorle

aleatoare Crandom walk, īn engleza) : piata flnanclara eficienta Impllclta, cel putln īn

varlanta de eflclenta slaba (autocorelatie neglijablla).

Princlpala caracteristlca urmarlta si "exploatata" īn gestlunea unul portofoliu este

reducerea si chlar ellminarea risculul speclflc prin diverslflcarea tltlurilor. Pun§nd ouale

īn mai multe cOsurl se reduce senslbll riscul de a le sparge printr-o manlpulare greslta a

lor. Slgur ca dlverslflcarea nu poate apara proprletatea (multlmea oualelor) d.e fenomene

exterioare (furtuna, grindlna etc.). Am utillzat dellberat aceasta metafora īntruc§t prin-

si rentabilitatea ceruta 158

clpiul dlverslficarli se asociaza cel mai semnlflcativ cu recomand- area īnteleapta de 'la nu

pune toate ouale īn acelasi paneril. ,

3.8. Rentabilitatea si riscul unui portofoliu de doua titluri

Un portofoliu de doua titluri se constituie īn proportii diferite de participare a unuia si a altuia dintre titluri (1 si 2). Din multimea de combinatii posibile (teoretlc, o infinitate) numai o parte a acestora este eficienta. Din submultimea de portofolii eficiente numai unul singur este optim pentru investitorul cu aversiune fata de risc.

Ecuatiile de portofoliu

Se refera la:

- rentabilitatea medie a portofoliulului R_p sau rentabilitatea sperata a porfofoliulului [E(R_p)] este media ponderata a rentabilitatilor sperate (medii) ale celor doua titluri E(R₁) si E(R₂) :

E(R_p) =x E(R_p) + (1-x) E(R₂)

Sau

R_p = x R₁+ (1-x) R₂

in care:

exprima ponderea de participare a unui titlu la constituirea portofliului "P".

Rentabilitatea portofliului este deci direct proportionala cu rentabilitatile titlurilor componente dar si cu ponderea de participare a fiecarui titlu la compunerea portofoliului. Pentru a creste rentabilitatea portofliului ar fi suficient sa crestem ponderea titlului celui mai rentabil. Dar aceasta crestere de rentabilitate este īnsotita de cresterea corespunzatoare a riscului. Suntem animati de a cerceta modul de interactiune a riscurilor celor doua titluri.

Riscul atasat unui portofoliu (s²_p) este o combinatie īntre dispersiile (s s²₂) ale fiecarui titlu component, īn functie de ponderile de participare la formarea portofoliului:

īn care 011 = covarlatia dintre abaterile probablle ale rentabilitatiior Rl si RJ, īn raport

cu speranta lor matematica:

ail

N

= a Proa . [Rj. - E (Rj )] tRt. - E (Rj )]

,s=l

= E [Ria - E (RI ) ] [RI. - E (RI )]

unde: 5 - - 1;2...N stari poslblle ale naturil īn perioada de prevlzlune;

Probg = probabilltatlle asociate flecarel stari posiblle a naturll.

Covariatla oil se poate determlna si pe baza coeflclentulul de

abaterilor medll patratlce ale celor 2 titlurl (oi si 01):

corelatie cPlj) si a

rn fapt, riscul unul portofoliu este suma elementelor unei matrlcl patrate a comblnatlilor īntre riscurlle celor doua tltlurl. Totalitatea covarlatlllor īntre rentabilitatiie celor doua titlurl Clnclusiv covarlatia rentabilitatii fiecarul titlu cu ea īnsasi = dlspersla) formeaza 0 matrice patrata (covarlance matrlx, īn engleza) a carel dlagonala cuprinde dlsperslile celor doua tltlurl (a si of) : .

Tltlul

Tltlul

Riscul portofliulul (OZp) se obtlne prin ponderarea covariatlllor cu ponderile Cx si y) de * partlclpare a tltlurllor nl constitulrea acestula :

OZp =

= x2a+y2of+2xyoI)

lx,YI

PI) . aj . a)

* a acelaŗi rezultat se ajunge

a=x-Ri+y-Rj iar E(RP)=x

si prin dezvoltarea relatiei oZp = E [R - E (Rp )]2 fu care

E (Ri ) + y . E (Rj ).

1a

TE08lA FlNANCIARA si GESTlUNEA pomOFoliuWI

9.2. Tipuri de corelatii rentabilitatearisc īntraun portofoliu

de doua titluri

In raport cu coeflclentul de corelatie PU' īntre rentabilitatiie celor doua tltlurl se pot identlflca 3 tipurl de corelatie extrema: pozitiva, zero si negativa.

Corelatia strict pozitiva este aceea īn care coeflcientul de corelatie este egal cu unu a11 = 1), cand unei cresteri a rentabilitatii prlmulul tltlu "1" n corespunde 0 crestere, īn aceeasi maSUra, a rentabilitatii celul de-al dollea tltlu "1" Cvezl flg g.l.a.). Riscul portofoliulul acestor tltluri, total dependente unul de celAlalt, este cel mai mare; la flecare crestere a rentabllitatll portofliulul are loc 0 crestere dlrect proportlonala a risculul.

Drept urmare, pe dreapta de corelatte rentabilitate-risc a unul 8stfel de portofoliu nu vom gasl vreo comblnatie de tltlurl mai performanta decat detlnerea Integrala a unula sau a altula dintre tltlurl Cvezl flg. g.l.b) :

B)

Rentabllltate

51a

b)

a

5J RlsG

Rentabllitate a1 = 1

Flg.9.1. Corelalla strict-pozltlva tntre doua titlurl ce compun un porfofoliu

Corelalla nula Czero) este egala cu coeflclentul zero de corelatie (P11 = 0), īn care rentabilitatiie celor doua titlurl varlaza īn tlmp total Independent. Absenta vreunei corelatll face ca riscul portofliulul Sa se dlmlnueze Cvezl flg. 9.2. 5 si b) .

EVAWAREA si GESTlUNEA PORrOFOUILOR

a = xZof + Y2a

īntruc§t 2xyoU = 2xy PU 01 01 = 0

. Ca urmare a dlmlnuarll risculul portofliulul de tltlurl Independente, exlsta 0 comblnatie optlma CM) īntre tltlurlle componente, care conduce la portofliul cu varlanta mlnlma absoluta CPVMA, vezl flg. 9.2.b).

Dln punctul l p§na-n punctul M avem comblnatll, īntre titlurlle "1" si nJII, care conduc progreslv spre cresterea rentabllltAtl1 portofoliulul, īn conditlile dlmlnuarll risculul 8ces-tula. Punctul M evldentlaza porfofoliul cu varlanta mlnlma absoluta CPVMA). rn con- tlnuare, pe curba M l (frontiera eflclenta) se obtln cresteri de rentabllltate a portofliulul dar cu asumare de riscurl dan ce īn ce mai marl Cvezl flg. 9.2.b.)

īn care PII = 0

Rentabilitaa a1=0

Flg.9.2. Corelatiaa doua tltlurl Independentee

Corelatiastrlct negatlva, īn care coeflclentul de corelatie este egal cu l Imlta sa Inferioara cPll = -1), este aceea īn care cresterea rentabilitatii titlului "1" este īnsotlta de 0 scAdere, īn egala maSUra, a rentabllitatll titlului complementar 11J" Cvezi flg. 9.3.a.).

Riscul unul astfel de portofoliu de tltlurl, total dependente negatlv, este cel mai mlc. 0

Rentabllitaa a1=-1 Renabflitate

a) b) .

Fig.9.3. Corelatia strlct negativa lntre doua tltlurl ce compun un portofoliu

1a TEORIA FlNANCIARA si GESTlUNEA pomOFOUUWI

comblnatie optlma a celor doua titlurl conduce chlar la risc zero al portofliulul Cvezl flg.9.3.b, punctul M).

02 = aa + Y2a +2xYull

īn care U1) = (-1) U1 ; 0] -

rn aceasta comblnatie optlma CM), prlmll dol termenl al ecuatiel sunt egalatl (negatlv) de termenul flnal, decl: 4 = 0 -

Trebule remarcat faptul Ca, īn general, corelatllle negatlve sunt foarte rare pe piata flnanclara cu atat mai pualn cele perfect negatlve. Cele mai multe sunt corelatllle slab pozltlve.

9.3. Aplicatii

Vom prezenta la fnceput sltuatla si parametril antlclpatl a doua portofol II a cate doua tltlurl strlct corelate (pozitia1 negatlv). Vom fncileia cu exemplul mai general al portofoliulul de tltlurl cu corelatie de mai mlca Intensltate.

Cl) Un Investltor flnanclar se Intereseaza de performantele portofliulUI (Rp sf 4) ce se poate forma īn ponderi egale Ccu 0,5) dln actlunea "1" a unei īntreprinderi de tratamente asfaltice si dln actlunea nln a unei īntreprinderi de fabrlcatie a gudroanelor asfaltlce.

Dln statlstlca rentabilitatiior anterioare s-a constatat 0 varlatie destul de sem nlflcatlva determinata de starea vremll Czlle īnsorlte, cer acoperit si tlmp plolos).

Tabelul 9.1. prezlnta frecventa (si deci probabllltatea) celor trel starl ale naturli, rentabilitatiie 8s0clate acestor etarl si calculele de antlclpare a sperantel de rentabllltate si de risc ale actlunilor'si ale portofliulul:

Tabelul 9.1.

StArl ale Rl. - )2 . Rt. Rt. - a (RI9-a1)2. (RI.-a1)2 .

naturll . Probab . Probab (RJ.-aT)2 .

EVALUAREA si GESTlUNEA PO8rOFOUILDR

Ptj = 94,65 = 1 = corelatie strict pozltlva

Rp = 0,5 . 7,5 + 0,5 . 6,5 = 7 %

4 = 0,a . 110,85 + 0,# . 80,58 + 2 . 0,5 . 0,5 . 94,65 = 95,25 pct.

a = 9,7596 pct.

Riscul unul astfel de portofoliu nu s-a dlmlnuat, el reprezlnta īn fapt medla ponderata a riscurllor tltlurllor componente.

Aceasta 1lpsa de amellorare a parametrllor portofliulul 8pare mai evldenta pentru tltlurl corelate strlct pazltlv si care 8U 8celeasl caracteristlcl: .

PII = 1 ; RI = RI; a = 0?

si care partlclpA īn mod egal Cechlponderat) la formarea portofliulUl

(a = a = 0,5):

Rp = x . Rl + x . Rj = 2"x . Rl = 2 .0,5 . Rl - - RI = Rj

oZp = 2X2a + 2 . x . x . 1 . a1 . a1

= 4 .X2a

= 4 . 0,25. a

=a=00. . .

rn concluzle, rentabilitatea si riscul acestul portofoliu sunt aceleasi cu ale tltlurllor componente si decinu avem nlcl 0 amellorare a performanael prin dlverslflcare.

TEORIA FlNANCIARA si GESTlUNEA PORrOFOUUWI

C2) ExemplUI care u,.meaza se sltueaza la cealalta extrema a coeflclentulul de

corelatie a11 = -1). EF'e cazul unul portofoliu egal constitult dln actlunea "111 8 unei īntreprinderi speclallzate īn confectlonarea artlcolelor de turlsm Cde plala, de sport, de agrement īn general) si din actlunea njn a unei īntreprinderi speclalizate īn confectlonarea de umbrele SI īmbracamlnte Impermeablla. Sltuatla rentabilltatllor īnreglstrate anterior īn functie de aceleasi trel starl ale naturll si calculele de antlclpare sunt prezentate īn tabelul nr. 9.2.

Tabelul 9.2.

Starl ale naturil Cs) īnsorlte

PII = -140,25 = - , 0,9993 8 -1 , corelatie strict negativa.

Rp = 0,5 . 10,5 + 0,5 . 3,5 = 7 %

-0,# . 206,85 + 0,# . 95,25 a 2 . 0,5. 0,5. 140,25 = 5,4 pct.

Op = 2,3 pct.

a = 0,77.

19,7'a =

RI

Dlmlnuarea risculul unul asl rentabilitatiie RI SI RI nu sunt pelel de portofoliu este ect corelate negatlv, Plt a)roape totala Ccu foarte putln -0,9993). fntr-un porfofoliu

EVAWAREA si GESTlUNEA PORTOFOUILDR 185

echlponderat (RI = RI , a = u1' a = a = 0,5) si cu corelalle perfect negatlva

ail = -1 ) riscul este complet ellmlnat (4 = 0). Rentabilitatea lul (np) ramane īn contlnuare egala cu rentabllitatea fiecarul titlu component:

Rp = x . Rl + x . RI = 2 . x . Rj = 2 . 0,5. RI = RI = RI

UZp = 2 . X2a + 2 . x . x . (-1) uj . uj = 0

fn realltate nu fntalnlm corelatll strlct negatlve. Chlar si-n exemplul de mai SU8 unde s-ar Justlflca 0 astfel de corelatie am fost nevola1 sfi 8dmltem 0 mlca, foarte mlca 1llmperfectlunen a corelatiei tltlurllor 111" SI 11JII. .

C3) Pentru generalizare apelam la portofolille ce pot fl constituite īn proportil diferite de partlclpare a unei actiuni 111'1 SI a unei obllgatiuni 11JII. Antlclparea parametrllor por-tofoliulul se face pentru un an polltlc agitat īn care au loc alegeri locale, leglslatlve $1 prezldentlale. #llnd vorba de tltlurl ale unor socletatl cu 0 pozltie Importanta īn economla natlonala, rentabllitatlle lor au 0 volatilitate ridicata īn rapoat cu evolutla sltuatiel polltlce dln tara. Nemultumlrlle acumulate fac ca $ansele lor Sa fie mlci si relatlv egale cu 20% pentru flecare dln cele doua tabere. Tabelul urmator prezlnta estlmarlle prIvlnd ren-tabilitatiie tltlurllor $1 corelatiaCmai slaba) dintre ele:

Sarl ale naturll a RI.

Tabelul 9.3.

rEORIA FINANCIARA si GESTIUNEA PORrOFOUUWI

. Ptl = 0,36 = 0,29; corelatie pozitiva de slaba Intensltate

rncep§nd cu acest exemplu vom testa' mai multe combinatll posibile Cteoretlc numarul ior este Inflnit) pentru a evidentla frontiera eficienta si pentru a ldentlflca portofoliul cu varianta Ccu risc) mlnim absoluta CPVMA, a se vedea subcapltolul urmator). Tabelul nr. 9.4. slntetizeaza rezultatele acestor comblnatli echldlstante Cpentru exempliflcare s-a ales 0 varlatie de a 20 pct. īn compozitla celor doua tltlurl Incluslv comblnatla PVMA) :

Tabelul 9.4.

Rp

a,1128

Pe masura ce creste ponderea obligatiunil "11' īn constltuirea portofliulul are loc dlminuarea risculul total al portofliului si a risculul marginal īn raport cu varlatia constanta Cdlrect proportlonala) a rentabilltatll acestula. Aceasta dlmlnuare se fI.lreglstrea-za p§na la 0 anumlta comblnatie optlma ce constitule portofliul cu varlanta mlnlma absoluta CPVMA: 3216%, 67,4%). Dincolo de aceasta comblnatie optlma evolutia risculul oZp īsi schlmba sensul : īn tlmp ce rentabilltatea Rp contlnua Sa scada constant, riscul oZp īncepe Sa creasca exponential.

Aceste observatil ne vor fl foarte utile īn identiflcarea frontierei eflciente si a PVMA.

Dar mai īnt§1 Sa observam parametrll unui portofoliu echlponderat CRT = RI' a = af' a = a = 0,a de tltlurl total Independente ail = 0 ) :

Rp = x . Rl + x . RI = 2 . x. Rj m 2 . 0,5. Rj = RI = RI.

EVALUAREA $1 GESTlUNEA PORrOFOUII.DR -.

4 = 2'X2'a+2'X'X'0'ul'ul =

= 2 ..0,# . a = 2 a 0,25. a = 0,5. a = 0,5. of

Daca rentabilltatea Rp ramane in contlnuare egalA cu cea a orlcarul tltlu, riscul a:

se reduce proportlonal cu (atentie 1) numArul de tltlurl echlponderate dln portofoliu a = a). Aceasta concluzle este esentiala pentru vlrtutile dlverslflcArl1 por.foliulul (asa cum vom vedea mai tarziu).

9.4. Frontiera eficientA. Portofoliul cu variantA minimaiA

absolutA (PVMA)

Obiectlvul uRmARIT in gestlunea eflclenta a portofliulul este gasirea celei mai perfoamante combinatll de tltlurl la un nlvel de risc dat, respectlv cel pe care Investltorul este dlspus īn mod sublectlv Sa si-1 asume. fn conseclnta, trebule cautat locul geometrlc al tuturor comblnatlllor performante posiblle pornlnd de la cea cu risc mlnlm. Aceasta cercetare conduce la ldentlflcarea "frontierel eflclente si a portofliulul cu varlanta mlnlma absoluta. .

Reluand rezultatele Ctabelul 9.4.) si graflcul (fig. 9.4.) dln ultimul exemplu, se pot evldentia douA categorll de comblnatll Cde portofolll) poslbile ale celor doua tltlurl componente ("1'1 si 11JII) :

- portofolll domlnate, respectlv comblnatllle de pe curba PVMA J, total Ineflclente:

scaderea rentabilitatii 8cestor portofolll este īnsotita (atentiel) de cresterea risculul acestula:

- portoaolll domlnante, superioare cresterea rentabilitatll este īnsotlta, īn

asumate. Pentru riscul portofliulul egal cu cel al obligatiunil 'IJlll avem doua comblnatll poslbllel Cx = 0 si x = 0,6518), cu rentabllltatl dlferite Rp(x = 0) = 412 si RpCx = 0,6518) = 6. Este loglc Ca, la ac,.elasi risc, se va 8lege portofoilul domlnant Cx = 0,6518) .cu rentabllltate mai mare CRp =6).

celor anterioare, mod natural, de sltuate pe curba PVMA, 1: riscurl mai marl ce trebule

1) Din ultimA earesie mATEmATICA a dispersiei portofoliuluide doua titluri (sau de n titluri) se REmARCA e,dstenta unei ecuatii de gradul doi cu 0 necunoscutA (x) si dea cu doua solutii posibile. Pentru cazul ANaIizaT ecuatia devine 1.84a - 1,a = 0, de unde se obtin solutiile evocate mai 5us: xl s 0 sia , = 0,6518.

1a TEORIA FlNANClARA si GESTlUNEA PORTOFOlJUWI

Multlmea portofollllor domlnante, pornlnd de la cel cu risc mlnlm CPVMA) pentru

Investltorul cu averslune la risc si a

i 1 l l

īn care, constanta 2 este Introdusa pentru slmpliflcarea ecuatiel.

Rezolvarea functiel de mlnlmlzare se face prin slstemul de derivate partlale

functiel Lagrange īn functie de cele clncl necunoscute (xl , X2 , x3' Al si A2) :

ale

TEORIA FlNANCIARA si GESTlUNEA PORTOFOUUWI

a-- Xl=ax)atj

J

aL =aXI-EI

t.

LAA2=aX'=1

Al Et + A2

= E.p

Sub forma matrlclalA, slstemul de ecuatll de mai 5us se poate scrle astfel:

Ll

E2 E3

0J

LA2J

Ll J

a12 a13 El

AZZ A23 E2

a32 a33 E3

W

X -

Solutllle cautate (a, Al , A2) vor fl gaslte prin rezolvarea slstemulul matrlclal:

X a

K,

īn care W-l este matrlcea "Wn Inversata . Ecuatllle parametrlce ce se vor construl dln

ultlmul slstem matrlclal ne permlt ldentlflcarea portofollllor eflclent e Cdeci8 frontierel

eflclente) pentru 0 speranta de rentabilltate scontata 8 portofliulul (a).

178 . TEORIA FlNANCIARA si GESTIUNEA PORrOFOUUWI

Pentru determlnarea frontierel eflclente se proCedeaza la mlnlmlzarea functiel

Lagrange: . - -

L = Mln 4 + Al [a1 + 3X2 + 4x3 - E:] + A2 [Xl +a X2 + x3 - 1 ]

īn care 4 = 10,4x2+4,2x: + 5a +2 . 1,2xlx2+2 .2,4Xlx3 + 2. 0,8x2x.3

Slstemul de derivate partlale devlne astfel:

axl = 10,4xl + 1,2x2 + 2»4x3 + 6Al + A2 = 0

aL = 1,2xl + 4,2x2 + 0»8x3 + 3Al + A2 = 0

ax3 = 2,4xl + 0,8x2+5x3 +4Al +A2 = 0

aAl = 6 xl + 3 X2 + 4x3 + 0 + 0 = E.p

= Xl + X2 + x3 + 0 + 0 = 1

rn exprlmare matrlclala obtlnem urmatorul slstem:

1,2 4,2 .D,8 3

L 1 1 1 0

0j LA2J

Ll J

Matrlcea Inversa Wl are urmatoarele valorl:

l .

MODEUTL Markowitz DE DIVERSIFlCARE A PORTOFOUUWI

L-1,166 1,6679 0,498 4,878 -0,2084]

ln

Slstemul de ecuatll parametrlce va fl decide forma:

. = 0,3434 . E.p - 1,166

. = -0,31321 . E.p + 1,6679

= -0,0302 . a + 0,498

= -1,3502 . a + 4,978 .

TA2 = 4,978 . E.p - 0,2094 ,

Pentru d lferite valorl date Cdorlte) ale sperantel de rentabllltate Ea obtlnam

urmatoarele valorl ale frontierel eflclente Cincluslv ale PVMA).

xl - 13,6% 10% 20,8% 55,1%

. Tabelul 10.2.

Prlmul portofoliu (pentru E: =3%) este domlnat de m _ultlmea portofollllor eflclente.

La acelasi risc CO'p = 2,06) se poate ol;tlne 0 rentabllltate superioara Cīntre 4 si 5%, a se

vedea flg. 10.1.).

TEORIA FINANCIARA si GESTlUNEA pOmOFOUUWI

- Din multlmea de portofolll eficlente, ultimul (pentru Ea = 6 % ) este nelegltim Cx2 =

-21,1% <0). Aceasta īnseamna Ca tltlul dol este vāndut la descoperire, lar banll īncasatl

. .dln aceasta operatlune sunt plasatl īn tltlurlle 1 si 3 Cīn plus fata de bugetul Initlal).

0 concluzle interesanta se desprinde dln graflcul de la flg. 10.1. Rentabllltatile

Indlvlduale ale tltlurllor pot fi obtlnute din comblnatii eficlente ale lor īn portofolil cu risc

mai mic. Daca piata financlara ofera aceasta performanta Cmlnlmizarea risculul la 0

rentabllltate data) atuncititlurlle cu risc mai mare devln neperformante. Pentru un risc

a = 4,a tltlul dol are 0 performanta Inferioara unui portofoliu eflclent care, la acelasi

risc, poate avea 0 speranta de rentabliitate apropiata de 5% (cu mult superioara

sperantel E2 = 3%). .

a l l' l l l

Frontiem efidenM

l .1=3

aa jl=2

aaaa

Portotolil

doain*

i

l = 1

. Fig. 10.1. Frontiera Ma'kowitz a combinatillo' celor trel titluri

īn aceste condltii, piata flnanclara ofera 0 "hon.ma" de rentabilitate pe unitatea de

risc. Aceasta norma va fi 0 referinta fiablla pentru a stabili rentabilitatea ceruta de

Investitor. Managerul flrmel emitente va trebui Sa faca remunerarea activulul riscant

(prolect de Investitll, titlu flnanclar etc.) cel putin la aceasta rentabllitate normata.

Evaluarea acestui activ riscant se va face deci īn raport cu aceasta norma de perfor-

manta a pietel flnanclare.

MODEWL Markowitz DE DIVERSIFICARE A PORTOFOUULUI

10.3. Rentabilitatea si riscul unui portofoliu format

din "n" titluri

Rentabllitatea unui portofoliu de 'Int' titluri este media ponderata a rentabilitatllor

medii CRT) ale tltlurilor care-1 compun. fn mod necesar aceasta se va afla īntre 1lmltele

prlvlnd cea mai buna si cea mai slaba rentabllltate a tltlurllor care compun portofliul, īn

functie de ponderile ce se acorda titlurilor componente CXI):

n

Rp = a xl

unde l =1; 2....n feluri de tltlurl dln portofoliu.

Rentabilitatea portofliulul este deciIndependenta de corelatlile dintre rentabllitatile

Indivlduale ale titlurilor componente. Nlcl 0 comblnatie a tltlurllor nu va duce la 0

rentabilltate a portofliului superioara celel mai mari rentabiiltatl indlvlduale.

rn conformltate cu avantajul diverslflcarll unui portofoliu se poate aprecia Ca riscul

acestula depinde, īn primul rand, de numarul de titluri care n compun Cca urmare a

compensarii varlatlllor contrare ale rentabilitatll acestor tltluri). rn acelasi timp, este

semnlficativa structura porfofoliulul: daca titlurile au ponderi relatlv egale īn com-

punerea portofoliuiul, atunciriscul acestuia este mai mic decat atuncicand 0 actiune

detlne 90% din portofoliu, lar celelalte actiuni OCUpa restul de 10%. Pe de alta parte, un

portofoliu, compus dln actiuni ale unor socfetatl recunoscute si Importante, va fl mai

putln riscant decat un portofoliu ce cuprinde titlurl ale unor socletatl micl si care nu

coteaza la bursa. rn sfarslt, un portofoliu dlverslflcat pe mai multe ramuri economlce va

fl mai putln riscant decat portofliul care cuprinde tltlurl dlntr-o slngura ramura.

rn slntezA, riscul unul portofoliu deplnde de trel factorl:

1) riscul flecarel actiuni Incluse īn portofoliu;

2) gradul de Independenta 8 varlatlllor actlunilor īntre ele.

3) numarul de tltlurl dln portofoliu.

Riscul acestul portofoliu poate Sa rezulte dln urmatoarea matrlce a disperslllor (001)

si a covarlatlllor (001) rentabilltatllor tltlurllor componente:

n

aaa

aaaaoll =

l 1a1

(N2 - n ) covarlatll

n n

a a xl a 011

n dlspenll

l ... aa aa aann

TEORIA FlNANCIARA si GESTlUNEA PORTOFaUWI

a a

N2-N covarlail oia

cula1

N2-N

, -2- covarla11 oil

n dlspersll oil

cula1

Riscul portofliulUI de nnn tltlurl rE prezlntA decisuma tuturor comblnatlllor poslblle

īntre variatille de rentabllitate ale titiurllor componente Clncluslv proprlile dlspersll), īn

functie de ponderile de partlclpare a tltlurllor la compunerea portofliulul.

10.4. Selectia portofDliului de nnn titluri

lpoteze ale modelului Markowiaz:

1. Crlteriul de selectie a camblnatlllor eflclente de nn" tltlurl este cel cunoscut:

"speranta-d lspersle".

2. Toate cele "n" tltlurl sunt riscante, caracterizate printr-o anumlta speranta de

rentabllltate CEI), dlspersle (a a all) si covarlatie cu flecare dintre celelalte tltlurl dln

portofoliu. .

3. Rentabilitatea scontata a portofliulul (Ea) este 0 varlablla exogena modelului fllnd

furnlzata d In afarA de aaatre Investitorl. Compozitia eflclenta a portofliulul Cun punct

speclflc pe frontiera eficlenta) trebule Sa determlne 0 medle ponderata a sperantelor de

rentabllltate ale tltlurllor (EI) egala cu (Ea):

aXIEI = E*p

Sub aceste lpoteze, problema de selectie a portofolillor eflclente Clncluslv a celul

cu varlanta mlnlma absoluta = PVMA) corDsta īn mlnlmlzarea risculul OZp la 0 speranta

de rentabll ltate scontata Ea: .

MODELUL MAR 1<0VlTZ DE DrvERSIFlCARE A PORTOFOUUWI

Mln a a xl >1 all

i l

stlind Ca: a xl EI = E.p

l

a xl

i

Pentru mlrimfzarea unei functii sub restrlct'l ae recurge la functia Lagrange.

L = Mln a a xl xl all + a1 X.IEI- +a2 xl - 1

l l l l

Compozlala eflclenta a portofliulul īn xl cu l = 1,2...n, sub restrictlile prlvlnd Ea si

Investlrea Integrala a bugetulul Investitorulul se determina prin sistemul de n +2 derivate

partiale egalate cu zero:

n

= a a ail + a1 EI + a2 . 1

Bxl 1=1

n

= a xl E, = E.p

Bal 1=1

BL n

= a x = 1

Sub forma matrlclala, slstemul de ecuaa11 de mai 5us devlne:

a12 ... aln El

a ... A2N

E2

a

an2 ... 02 En

E2 ... En 0

W

TEORIA FlNANClARA si GESTlUNEA POaFaUWI

Solutla cercetata, sub forma matrlclala, este X = W-l . K Ecuatllle parametrlce

astfel rezultate ne conduc la compozitia porfofollllor eficlente (frontiera eflclenU)

pentru orice speranta de rentabllltate scontata de Investltorl (Ea) īn functie de profllul lor

de risc.

Pentru ldentlflcarea portofliulul cu varlanta minlma absoluU PVMA se porneste

de la aceeasi expresle a risculul portofliulul cu 0 slngura restrlctie prIvlnd alocarea

bugetulul Investltorulul nriscofob".

1a

Mln aa xl.xioll

. l J

stiind cA: a xl

l

Functla Lagmnge pentru PVMA va fl decimai slmpla Ccu un slngur multlpllcator

a1):

L = Mln a a xl xl 011 + a1 xl -

l J l

Sub formA matrlclalA vom avea urmatorul slstem de derivate partlale cu n + 1 ecuatll:

Ll

LalJ

LIJ

K

012 ... 01N

a ... 0a

On2 ... a

Portofol lul cu varlanta

temulul matrlclal X = H-l

a, PVMA poate fl:

- legltlm, cu toate ponderile a pozltIve: xl a 0 pentru V l - - 1,2...n

mlnlma absoluta CPVMA) se va obtlne prin rezolvarea 815-

. K. rn functie de natum pozltlvA sau negativa a ponderilor

MODELUL MARKOVlTZ DE DIVERSIFICARE A PORTOFOUULUI

- nelegitlm, care adrnite si ponderi negative xl > 0 si xl < 0 dar cu respectarea

restrlctiei PVMA: a xj = 1.

i

Calculul riscului presupune cunoasterea a 'In" sperante de rentabilitate, a "nll dlspersli

si a n(n-l) informatii predeterminate. Pe masura cresteril numarulul de titluri dln

portofoliu asistam la 0 crestere exponentlal.a a numarulul de Informatii necesare īn

modelul Markowitz. Acest "apetit pantagruelic" de Informatii constltule principala 1lmlta

a modelului Markowitz. rn modelul sAu diagonal Sharpe reduce considerabil necesarul

de informatil Cla 3n + 2) ceea ce face ca modelul SaU Sa fle mult mai operatlonal. rn

tabelul 10.3. se prezinta comparativ necesart'l de informatii pentru diferite mariml ale

numarulul de titluri din portofoliu:

Tabelul 10.3.

Nr. de titluri

"n"

aodelul Markowitz

2n + n (n-l)

Modelul diagonal

3n+2

10.5. Riscul specific si riscul sistematic al portofoliului de

"n" titluri

Revenlnd la formula de calcul a risculul portofliulul de n tltlurl se ldentlflca UsOI cele

douA componente ale acestuia: riscul specific Cdiversificabll) si riscul slstematic Cde

piatA si deci nediversiflcabll) :

TEORIA FINANCIARA si GESTlUNEA PORrOFOUUWI

OZp = aaa + aaxlxloll

, l l 1

l = 1

l a 1

risc

slstematic

risc

speclfic

a

Se impun, credem, cateva remarcl prellmlnare prlvlnd riscul sistematlc. Dupa cum

rezulta dln expresia de mai 5us, acesta este determlnat de valoarea covarlatlflor tltlurllor

īntre ele. Or, valoarea unef covariatfl este functie de abaterfle standard ale celor doua

TFTIUTI (01 si 0'1) si de coeflclentul de corelatie a11) dintre rentabllitatile (RI si Rl) ale

tltlurilor anallzate: .

011 = Pll . 01 . 0'1

Varlabila care Intervlne supllmentar īn riscul slstematic fata de cel speclflc este decl

coeffcfentul de corelatie a11) care determlna natura (pozltfva sau negatlva) si marlmea

risculul slstematlc. un coeflclent negatlv va conduce, īn mod natural, la 0 marlme

negativa a risculul slstematlc si deci0 dlmlnuare (pana la ellmlnare, daca PII = -1) a

risculuf total al portofoliulul.

Din nefericire, corelatlile dintre rentabllltatile titlurllor financlare nu StlBt, dec§t foarte

rar, negative. Acestea sunt, cel mai adesea, pozltlve si de mlca Intensltate (asa cum am

mai aflrmat anterior si cum .rezulta, de altfel, din aplrcatia numerica de trel tltlurl). fn

conseclnta, riscul slstematlc are 0 marlme pozltlva mai mare sau mai mlca īn functie

ae coeflclentll PIl, de abaterile standard (01' 01) ai de ponderile (xl si xl) de par-

tlcipare a titlurllor la constltulrea portofoliului.

Existenaa, īn mod oblectlv, a corelatlllor pozltlve este 0 caracteristlca a pietei finan-

clare, respectlv a lichidltatll, transparentel si securltatil acestela. La randul lor, perfor-

mantele pietei flnanclare sunt determlnate de evolutla Indicatorllor macroeconomici

semnlficatlvl īn plan national si chlar Internatlonal CPIB, rata Inflatiel, rata dobānzll etc.).

rn functie de factoril macroeconomlci luatl īn calculul risculul slstematlc s-au dezvoltat

doua modele celebre: CAPM (Sharpe, Llntner, Mossln, Treynor) si APT CRoss). Pana la

anallzarea acestora mai avem mult "de furca" īn domenlul diversiflcarli pentru ellmlnarea

risculul speclflc.

Princlplul dlverslflcarfl eflciente Cdeterminarea frontierel eflclente) presupune

stablllrea, conform crlteriulul "speranta-dlspersle", a portofliulul cu varlanta mlnlma

pentru flecare speranta de rentabllltate scontata a portofliulul. rn modelul Markowitz,

pentru orlcare Investltor cu un profil de risc personal si cu un comportament ratlonal,

portofoliul eflclent ales este un portofoliu optlm dlverslflcat. .

MODEWL MARKOVlTZ DE DrvERSIFlCARE A PORTOFOUUWI

Dlverslflcarea Cchlar optlmA) 8rQ 0 1lmlta InsurmontabllA: riscul slstematlc. Prin dlver-

slflcare eflclenta putem Qllmlna riscul speclflc al portofliulul dar ramane dQ asumat Cde

catre Investltor) riscul slstQmatlc al acestula.

10.6. Situatia unui portofoliu echiponderat

Ellmlnarea risculul speclflc prin dlverslficare este 1lustrata īn mod semnlflcatlv īn

cazul pOrfofoliului echlponderat . Acesta este portofliul īn care toatQ cele nn" tltlurl

Intercorelate care-1 compun au aceeasi pondere , respectlv a "nn-a parte dln total:

)q - -. V l =1,2...n tltlurl.

-n'

La aceste ponderi egale se poate calcula usor 0 dlspersle medle 8 rentabilitatiior

tuturor tltlurllor Ca) si 0 covarlatie medle a1). fn aceste condlall, riscul portofliulul

echlponderat este:

4 = - n a + (N2-N) a1 = 1a + (1 - *) a1

N2 N2 n

La limlta, respectiv pentru n -. a, vom 8ve8 riscul unul astfel de portofoliu egal cu

covariatia medle a1) a portofliului, adica egal cu riscul de piata a = a1. Un astfel de

portofoliu este total (optlm) dlversiflcat, conducand astfel la ellmlnarea completa a

risculul speclflc Cdlversiflcabll, dlspersla medle = a). Slngurul care mai conteazA, īn

evaluarea acestui portofoliu, este riscui slstematlc, de piata Cnedlverslflcabll, covariatia

medie = a1).

Evaluarea acestui risc slstematlc presupune remunerarea lul pe piata financlara cu 0

prlma de risc de piata Cce va fl determinat prlri modelul CAPM). Riscul specific nu este

remunerat īntrucat el poate fl ellmlnat prin dlverslflcare.

Efectul diverslflcarlf īn functie de numarul de tltlurl este foarte blne 1lustrat īn cazul

porfofoliului de aslgurari care raspunde urmatoarelor lpoteze de lucru:

1. - portofoliu echlponderat: xl = - pentru

n

2. - toate titlurlle au aceeasi speranta CEI) si aceeasi dlspersiQ (a);

3. a toate titlurlle sunt independente dln punct de vedere statlstlc: Ptl = 0. rn con-

secinta, riscul sistematic al acestul portofoliu este egal cu zero.

Riscul total al portofliului este eg81 cu riscul SaU speclfic si deci dlverslficabll:

V 1=1,2...n;

lB6

TEORIA FINANCIARA si GESTlUNEA PORTOFOUUWI

= a a00 = 1 a00 = a

i a i n

Exemplu: Pentru 0? = 625, aceeasi pentru toate cele n titluri (polite de asigurare),

riscul portofoliulul īn functie de numarul n do titlurl evolueaza dupa cum urmeaza Ca se

vedeatabelul nr. 10.4.). .

Tabelul 10 4.

0,25 l

L.-

a

a

Mai multe teste emplrice au demonstrat Ca un portofoliu este suflcient de diversiflcat

daca este compus din 20-30 de tltluri. Dlncolo de acest numar, reducerea marglnala a

risculul specific este nesemnificatlva sl oricum inferioara costurilor antrenate de ges-

tiunea unor portofolil asa de mari Cvezl flg. nr.10.2.).

Riscul total al unul portofoliu nu poate fl dimlnuat, prin dlverslflcare, dincolo de 0

1lmlta de 30-40% ce reprezinta ponderea riscului de piata al portofliulul. Economla

nationala, piata financiara sunt, prin ele fnsele, variablle (variatla PIB, a Inflatiel, a

dobanzll, a cursulul valutar etc.). Aceasta varlabilitate a pletef flnanclare deflneste riscul

de piata si are proportii d iferite Cde la tara la tara) īn riscul total al valorilor moblllare.