Obecná diskrétní Fourierova transformace

1. Výchozí pojmy a vztahy

Obecný pohled na integrální transformace

Četné inženýrské aplikace se vyznačují výraznou potřebou uchovávat a zpracovávat množství informací, v nichž zkoumané veličiny vystupují jako rozsáhlé soubory spojitých či diskrétních dat. Mezi nejrozšířenější metody sloužící k jejich analýze patří různé typy integrálních transformací, jejichž společným principem je obecně 'poměření' zkoumaného vstupu množinou testovacích funkcí , kde L je vybraná množina indexů. Tato analýza - ve smyslu dekompozice - vychází ze vztahu

,

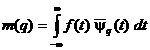kde pruhem značíme komplexně sdruženou veličinu, která tvoří jádro transformace.

Funkce zpravidla patří do množiny funkcí integrovatelných s kvadrátem mající nekonečně mnoho prvků.

Chceme-li při analýze rozlišit dvě funkce, musí být rovněž množina

testovacích funkcí Q nekonečná. Jen tehdy jsme také schopni rekonstruovat z hodnot . Říkáme, že je transformací funkce , v operátorové symbolice 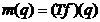. Inverzní transformace je pak syntézou z veličin a píšeme Tento výraz je často označován jako rekonstrukce nebo rozvoj funkce

Studium transformací v různých funkčních prostorech má bohatou tradici, přičemž jednou z klíčových otázek je výběr vhodného prostoru testovacích funkcí pro danou aplikaci. Přes různorodost přístupů existují některé společné požadavky, zejména

jednoduchost algoritmů pro výpočet transformace a její inverze,

dostatečná univerzálnost algoritmu,

jednoznačnost a stabilita algoritmu.

Poslední z podmínek zajišťuje, že malým změnám ve vstupních datech odpovídají také malé odchylky v transformaci. 353b18d

Z teorie Fourierovy transformace víme, má-li spektrum funkce finitní nosič, tj. spektrum je ohraničeno, pak při diskretizaci Fourierového integrálu dochází

k vyhlazování „špiček“ ve Fourierovském spektru ,

ke vzniku falešných „špiček“ (kmitů),

není-li spektrum finitní , pak vzniká překrývání spektra v důsledku nevhodné diskretizace spojité funkce, tzv. „aliasing“ či „mimikry“,

navíc při takto nepřesně vypočteném spektru, například v důsledku diskretizace, numerických metod nebo zatížení signálu náhodnou chybou, při rekonstrukci funkce (signálu) dochází k divergenci v normě , tj. k porušení stability řešení, jinými slovy, malým změnám ve vstupních datech odpovídají velké odchylky v řešení.

Při diskretizaci tzv. multiplikativního integrálu tyto nedostatky mizí.

Definujeme stručně multiplikativní integrál a multiplikativní systém funkcí.

Definice 1:

Multiplikativní integrál je obecně definován , zde množina funkcí tvoří multiplikativní systém.

Číselná realizace tohoto integrálu (za podmínky jeho konvergence) je dána přímo hodnotou integrálu vypočtenou obdélníkovou metodou, tj. zde N je počet bodů,

jsou funkční hodnoty v diskrétních bodech,

je krok vzorkování,

je diskrétní multiplikativní systém.

Definice 2:

Multiplikativní systém na je ortonormální soustava nenulových funkcí 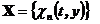, nIZ , pro něž platí, že pro každé IC k m:

soustava Cobsahuje jejich součin c_k c_m c_a IC

soustava Cobsahuje podíl C

Například soustava je multiplikativní, ortogonální na [0,1].

Patří k nim i soustavy Rademacherovu, Haarovu a Walshovu, které uvádíme dále.

Věta 1. Nechť f je měřitelná funkce na intervalu [0,1], potom rozvoj f dle úplného multiplikativního systému (báze lineárního prostoru) konverguje k  f skoro všude na intervalu[0,1]:~ .

Důkaz.

Částečný součet řady bude

resp.

Nechť číslo charakterizuje funkční hodnotu v bodech intervalu bázové funkce, tj. v bodech , potom .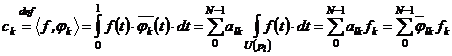

Čísla nezávisí na vstupu f, ale závisí jen na bázových funkcích .

2. Speciální diskrétní ortogonální systémy

Rademacherova soustava

Definice Posloupnost funkcí definovaná na intervalu

pro n = 1,2, 3,

Soustava je tzv. Rademacherova ortogonální soustava funkcí .

S výjimkou bodů pro tuto soustavu platí vztah:

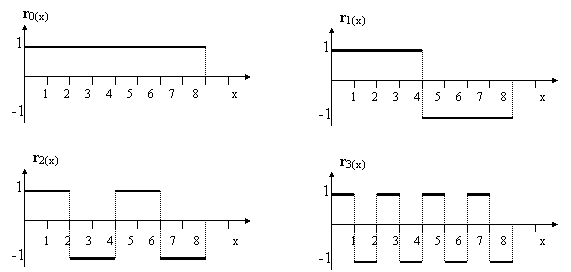
Konstrukce: Rozdělíme interval na stejných dílků a v příslušných dílčích intervalech položíme střídavě rovno +1 a -1. Například při systém bude tvořen , počet bodů je 8 a indexy p = 0,1, 2,,n-1

Matice R tvořená vektory a představuje Rademacherovu bázi.

Definice na základě dvojkového rozkladu čísla

zde z = 0,1, 2,N-1 a indexy k = 0,1, 2,n-1:

, n = 1,2,3,

Rademacherova soustava je tvořena stochasticky nezávislými funkcemi a v důsledku své jednoduchosti je velice rozšířená a používá se v teorie pravděpodobnosti při analýze náhodných procesů. Velkou výhodou této báze je, že index řádků matice souvisí s počtem nulových bodů v řádků (konkrétně

Grafická reprezentace Rademacherovy báze:

2.Walshův systém (Walsh-Paley)

Definice 4. Walshův systém je ortogonální v l₂ a je tvořen součinem Rademacherových funkcí a funkci

,

čísla m, p_k jsou určeny z dvojkového rozkladu čísla n :

například pro = 8 dostaneme

Walshova báze W je tvořena pomocí vektorů W_n , například pro N = 8: matice , n,k =0,1,,7

Výhodou Walshovy báze je, že je úplná, oproti Rademacherově bázi má však tu nevýhodu, že index řádku není totožný s počtem nulových bodů a proto ji lze obtížně přímo využít pro analýzu náhodných procesů.

Walshova modifikovaná soustava

Výhodou této báze je , že se jedná o bázi úplnou a navíc index řádku matice souhlasí s počtem nulových bodů.

Tuto bázi lze vytvořit rekurentně z Walshovy báze podle vzorce:

, zde p= 0,1; j=0,1,2,3,…,k; N=2^k.

Pro N=2ⁿ=8 platí modifikovaná WP báze W^*:

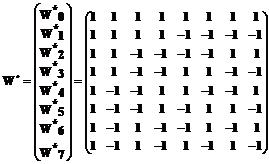
Haarova soustava

Dalším diskrétním ortogonálním systémem je Haarova soustava.

Definice 5. Haarův systém je ortogonální v l₂ a je definován na intervalu x I

, pro n = 1,2, 3,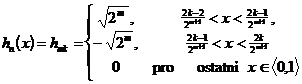

, m =0,1,2,, k = 1,2, ,2^m . Pomocí sestavíme matici H.

Pro názornost zvolme délku intervalu 8, což představuje počet subintervalů 2ⁿ =2

Haarova ortogonální báze bude

Někdy Haarův systém se zapisuje jako ortogonální systém pomocných funkcí:

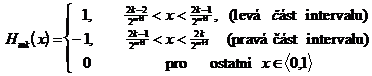
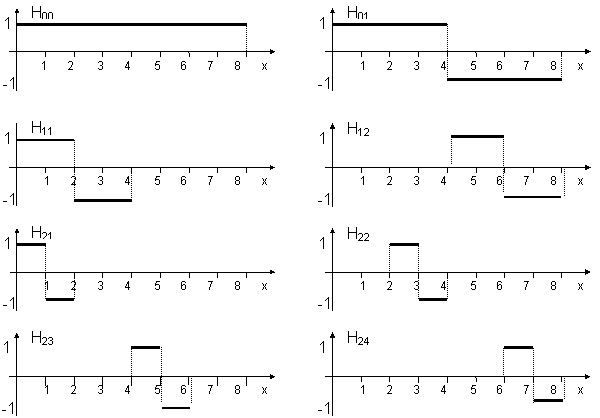
Abychom obdrželi Haarův systém ortonormální stačí matici H, popisující ortogonální systém pomocí funkcí vydělit , zde N je počet bodů.

3 Zobecněná Fourierova řada

Věta 2. Nechť jsou prvky prostoru l₂(n) a tvoří ortonormální bází (tj. úplný ortonormální systém) a nechť je libovolná číselná posloupnost (reálná nebo komplexní), potom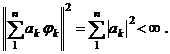

Důkaz.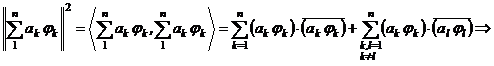

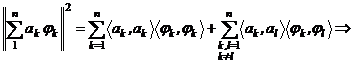
Jelikož tvoří ortonormální systém, pak ,

Potom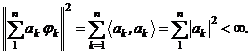

Věta Nechť N, každý prvek f lze rozvinout v konvergentní řadu (platí i pro ): kde koeficienty jsou .

Poslední řada se nazývá ortogonální nebo zobecněná Fourieriva řada,

Tato řada konverguje právě, když , pro ní platí Besselova nerovnost a Parsevalova rovnost. (Viz. Minimální vlastnost Fourierových koeficientů).

Protože všechny výše uvedené systémy jsou ortogonální, pak každý signál v prostoru l₂(n) lze rekonstruovat pomocí zobecněné Fourierovy řady.

přitom koeficienty , , v příslušném ortonormálním systému jsou určeny skalárním součinem :

, , zde

tvoří Walshovu bázi W ,

tvoří modifikovanou Walshovu bázi

tvoří Haarovu bázi H.

Rekonstrukci funkce f se provádí pomocí násobení matici inverzní k bázové matici W (resp.H) na vektor vypočtených koeficientů c, tj. f =W^-1c .

Rademacherova soustava v prostoru l₂(n) tvoří neúplný systém, pak výpočet koeficientů a rekonstrukce funkce je neúplná.

Příklad 1. Zvolme osm čísel, která budou představovat vektor dat Y = ( 3,1,6,2,3,7,9,5)^T.

Postupně vytvoříme jednotlivé matice bází a provedeme transformaci, tj. vynásobíme jednotlivé matice vektorem dat Y : resp. nebo

Výsledkem transformace budou koeficienty jednotlivých bází tvořené vektory

.

Zpětně postupujeme obdobně . Vytvoříme inverzní matice k daným bázím a postupně je vynásobíme příslušným vektorem koeficientů Výsledný vektor Y_x ( zde x je označení příslušné báze ) tvoří koeficienty zpětné transformace neboli rekonstrukcí vstupního vektoru a jak je vidět v tabulce, souhlasí s původním vektorem dat Y. V důsledku úplnosti použitých systémů rekonstrukce je u všech bází stejná.

4. Fourierova transformace (opakování)

Předpokládáme, že studenti jsou seznámeni s Fourierovou transformaci,např.v předmětu Integrální transformace, který se vyučuje ve ročníku. Připomeňme důležité vlastnosti Fourierovy transformace, na něž se budeme příležitostně odvolávat

Zavedeme pro stručnost označení pro Fourierův obraz: . Reálnou množinu všech t (časovou) budeme značit R, reálnou množinu všech (frekvenční)

Nechť jsou Fourierovy obrazy originálů , pak platí věty:

1) Lineárnost: jsou konstanty.

2) Podobnost (dilatace) originálu: reálná konstanta.

3) Substituce (kmitočtový posun, modulační věta):

kde reálná konstanta.

4) Posunutí (translace) originálu:

5) Derivování originálu:

6) Derivování obrazu: ,

7) Obraz integrálu originálu: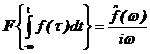

8) Obraz konvoluce:

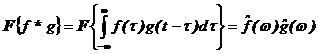zde

9) Obraz součinu:

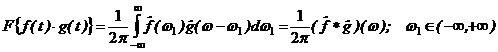
10) Inverzní Fourierova transformace je dána předpisem

.

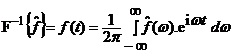11) Princip symetrie: definujeme-li Fourierův obraz takto:

pak zpětná Fourierova transformace bude

Znamená to, že v ortonormální bázi existuje typická symetrie mezi originálem, například časovou funkcí, a jejím obrazem ve frekvenční oblasti. Tedy, je-li Fourierův obraz funkce, potom funkce je Fourierovou transformací funkce a k výpočtu lze použit stejný algoritmus.

12) Parsevalova rovnost: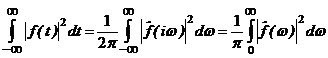

V ortonormální bázi: , potom a

tj. Tento vztah platí i v prostoru

Umožňuje určit energii signálu z obrazu signálu.

13) Plancherelova věta : :

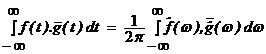
V ortonormální bázi: , potom a

5 Minimální vlastnost Fourierových koeficientů

Věta 4 Nechť 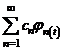je zobecněná Fourierova řada funkci , jsou koeficienty této řady a je ortonormální systém funkcí , potom Fourierův mnohočlen řádu n je nejlepší aproximací funkce f ve smyslu normy :

, tj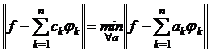

Toto kriterium lze vyjádřit pomocí integrálů :

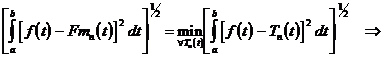
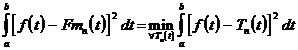
Důkaz. Provedeme důkaz pro reálnou funkci f(t) s použitím axiom a vlastností skalárního součinu v ortonormované soustavě funkcí :

= = =

=

= = =

= =

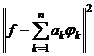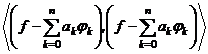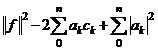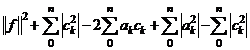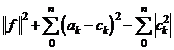
Je evidentní, že = 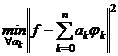bude právě, je- li .

Tímto věta je dokázána. 

Tento důležitý výsledek lze vyjádřit slovy: na intervalu má ze všech mnohočlenů n-tého stupně v bázi nejmenší střední kvadratickou odchylku od funkce f právě mnohočlen s Fourierovými koeficienty.

Teď lze napsat : = =

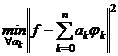Poslední výraz je znám pod názvem Besselova nerovnost,

při přechází v Parsevalův vzorec (Parsevalova identita): .

6. Diskrétní Fourierova transformace DFT

Definice 6. Nechť posloupnost patří do prostoru , pak diskrétní Fourierova transformace může být definována:

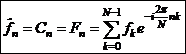(1)

resp. , resp., kde

N . . . celkový počet vstupních hodnot diskrétní (mřížkové) funkce,

. . . hodnota vstupní funkce v bodě k,

. . . koeficient n-té harmonické.

Označme: , pak je zřejmé, že můžeme vyjádřit ve tvaru matice pro různá n a k.

Matice bude mít tedy tvar:

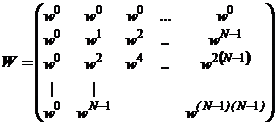(2)

Zde matice W je tvořená ortogonální soustavou funkcí na intervalu , . V případě ortonormální soustavy matice bude .

Diskrétní Fourierovu transformaci lze tedy vyjádřit takto:

, zde K je konstanta rovná 1 resp. resp.,

kde f vektor vstupních hodnot.

Maticový tvar zpětné diskrétní Fourierovy transformace bude: , zde K₁ je konstanta rovná resp. resp, 1.

Vlastnosti matice W:

Matice W je regulární a symetrická, tj.

a , zde I je jednotková matice.

2) Matici lze vyjádřit pomocí vztahu ,

kde je komplexně sdružená matice k matici W, tj. má prvky: .

3) W je unitární tj. .

Obecně W je unitární matici, jestliže platí : , tj.

4) W je permutační periodická matice 4. stupně:.

a , kde

P je permutační matice řádu N, která vznikne přehozením řádků jednotkové matice.

Pro matici P platí, že PP = I, zde prvek permutační matice

.

Potom matice bude mít prvky:

Je zřejmě, že , neboť

5) Vlastní čísla matice W jsou čísla : : ,

Bude-li přímá Fourierova transformace dána vztahem ,

pak zpětná Fourierova transformace bude

a vlastní čísla matice budou

6) Označíme –li druhý řádek matice W : , pak každý další bude , jednotlivé prvky kterého jsou mocniny prvků .

7) Prvky , k =0,1,2,…N –1, vektoru jsou kořeny rovnice

Čísla leží v komplexní rovině na kružnici o poloměru 1 a dělí tuto kružnici na N stejných dílů, počínaje kořenem , přitom platí, že

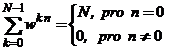a .

Pro n = N/2 a k=0,1,…,N (resp. k= N/2 a n=0,1,…,N) bude nk= kN/2 (resp. nk=nN/2),

potom .

Funkce je periodická s periodou mN, mI Z (tj.m=0,) :

Příklad 2.

Nechť je zadána posloupnost jako sloupcový vektor, pro :

Pro přímou transformaci použijeme tvar : , kde

matice je čtvercová matice řádu N x N=8 x 8.

Prvním úkolem bude sestavit matici bázových vektorů W.

Prvky matice W: se nachází na jednotkové kružnice (viz. obr.):

Vektor bázových funkcí :.

Matice po dosazení bude

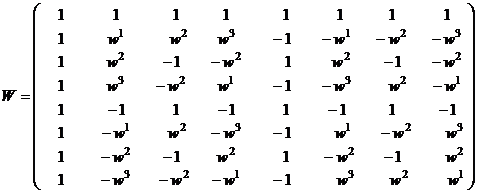
Dále násobením matice vstupním vektorem dostaneme spektrum :

Výsledek obsahuje 8 hodnot, přičemž druhou polovinu tvoří hodnoty komplexně sdružené k prvním.

Výsledek charakterizuje amplitudové spektrum a fázové , k=0,1,…7.

Poznámka.

Často se můžeme setkat s následující (dvoustrannou) definici DFT

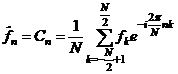, zde

N . . . celkový počet vstupních hodnot, (N je sudé),

. . . hodnota vstupní funkce v bodě k, , nabývá hodnot ,

. . . hodnota výstupní (DFT), , nabývá hodnot ,

nebo 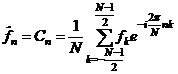, zde

, je liché , , .

Dvourozměrná DFT (stručně)

Nejdříve definujeme vícerozměrnou Fourierovu řadu.

Definice 7. Nechť xIR^k, (například xIR , tj. x=(x₁, x₂₎ resp. (x,y)) a nechť tvoří úplný ortonormální systém, L²(R^k), splňující podmínku, že pro každou funkcí L²(R^k) existuje jednoznačný rozvoj v konvergentní řadu:.

Tato řada konverguje v normě L² s koeficienty ,

Zde R^k , je míra (objem) elementu x, index Z.

Například, je-li k =2, pak se jedná o dvourozměrnou řadu, a koeficienty této řady budou =.

Ted´definujeme diskrétní dvourozměrnou Fourierovu transformaci na základě numerického výpočtu koeficientů .

Nechť oblast D představuje obdélník (nebo čtverec).

Tedy pro diskrétní výpočet lze tuto oblast popsat ve tvaru obdélníkové nebo čtvercové matice (například M x N nebo N x N).

Nechť index prvků, charakterizujících první proměnnou je přímo x =0,1,2,…,N-1 (sloupcový index), a index prvků, charakterizujících druhou proměnnou je přímo y =0,1,2,…, M-1, resp. y =0,1, …,N-1 (řádkový index), pak index n nabývá hodnot n = 0,1,2,…(M-1) (N-1).

Nechť sestavena matice je čtvercová, a nechť , pak koeficienty c_n budou tvořit matici řádu N x N.

Zavedeme označení pro sloupcový index koeficientů c_n jako v=0,1,…,N-1,

Pro řádkový index koeficientů c_n jako u=0,1,…, N-1 a nechť .

Definice 8. Definujeme teď .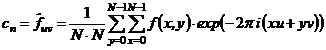

V případě, že oblast D představuje obdélník, pak

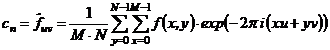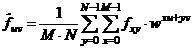=. (3)

Výpočet dvojdimenzionální DFT se provádí ve dvou etapách:

- nejdříve se vypočte jednorozměrná DFT v každém řádku, tj, F( u,y). Pro každý řádek u je konstanta, y je proměnná,

- pak podle sloupců, tj. pro každý sloupec v je konstanta a x je proměnná.

Transformaci lze počítat i obráceně, tj. nejdříve pro každý sloupec, pak pro všechny řádky.