On utilise une méthode de défuzzification dite centre de gravité. On constante que cette méthode effectue la moyenne des actions u pondérées par leurs appartenances mU(u)
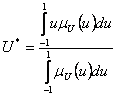(5.10)
Réglages pratiques
Le réglage de vitesse a un moteur asyncron avec regulateur flou prend en considération les points s 15215b14p uivantes. Tout d'abord, les constantes E et DE déterminent les plages de variations des variables d'entrées, et par conséquent les domaines où la commande évolue.
Ensuite, la valeur de U définit les variations maximales de la commande u, plus elle est importante et plus la commande est capable de réagir rapidement.
La figure 5.8 Présente les résultats de simulation pour le régle du vitesse pour un moteur asyncrone.
Les resultates presenté ou obtenir pour un moteur asyncrone triphasé avec les paramètres:
Rs=0.6592W; Rr=0.563W; Ls=Lr=0.0643H; Lm=0.06H; J=0.085; p1=2.
Pour le regulateur avec logique flou
dans le boucle de vitesse s'ont obtenir
les resultates:
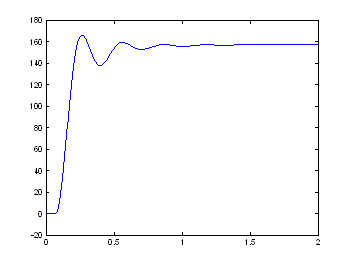
Fig 5.8 Raspunsul en temp le regulateur de vitesse avec logique flou à variation en étage a référence et a perturbation
Cette resultates s'ont
obtenir pour les paramètres et KDe=0,1; Ke=0,1, KDu=0,1; Ku=0,2.
Fig 5.81 Réponse en temp le regulateur de vitesse avec logique flou à variation en étage a référence et a perturbation
Cette resultates s'ont obtenir pour les paramètres et KDe=0,01; Ke=0,01, KDu=0,1; Ku=0,2.
Pour
une schéma de commande de réglage à vitesse
le moteurs asyncrone avec orientation apres flux rotorique avec autre tipe de
regulateur s'ont obtenir les resultates:
Fig 5.82 Réponse en temp à un étage de vitesse.
Synthése de regulateurs à vitesse avec methode CRONE.
Si dans la theorie de réglage automatique conventionel la réalisation des systèmes automatiques, on utilise un modèle de base avec un élement de retard de second ordre, dans le cas de la methode CRONE, le modèle de base est un element décrit par une équation differentielle d'erdre non entier avec fonction de transfert:
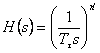(5.11)
ou 
est un nombre non
entier dans l'intervalle (1 - 2).
La phase de réponse fréquentielle pour l'action intégrale (5.11) d'ordre non entier est constante.
(5.12)
Dans le plan
Black, la relation (5.12) est representée pour une droite verticale d'abscisse 
, figure 5.9.a.
|
